New trends in estimation and inference

PyData NY 2019

Interpreting statistical outputs

Part of PyData NY 2019

Interpreting statistical outputs

After running a model, you get a point estimate with its CIs, and a p-value. What should we do with these terms?

The p-value has something to do with a null hypothesis

 What is the null hypothesis, anyways?

"Tiny p-values for tiny effect sizes in large datasets are probably due to violation of assumptions, not any "real" effect. Remember, the null model you are testing = assumptions+ H0"

source: @statsepi

"Tiny p-values for tiny effect sizes in large datasets are probably due to violation of assumptions, not any "real" effect. Remember, the null model you are testing = assumptions + H0"

source: @statsepi

Here's what you should worry about instead of p-values:

• Poorly-conceived research questions

Here's what you should worry about instead of p-values:

• Poorly-conceived research questions
• Poor data stewardship

Here's what you should worry about instead of p-values:

• Poorly-conceived research questions
• Poor data stewardship
• Sloppy research procedures

Here's what you should worry about instead of p-values:

• Poorly-conceived research questions
• Poor data stewardship
• Sloppy research procedures
• Poor measurement

Here's what you should worry about instead of p-values:

• Poorly-conceived research questions
• Poor data stewardship
• Sloppy research procedures
• Poor measurement
• Avoidable errors in the analysis

Here's what you should worry about instead of p-values:

• Poorly-conceived research questions
• Poor data stewardship
• Sloppy research procedures
• Poor measurement
• Avoidable errors in the analysis
• Wrong model altogether

Here's what you should worry about instead of p-values:

• Poorly-conceived research questions
• Poor data stewardship
• Sloppy research procedures
• Poor measurement
• Avoidable errors in the analysis
• Wrong model altogether

source: @statsepi

Try s-values instead

Try s-values instead

It's not a decision criteria (ex: not s-value > threshold), but a measure of "surprise" or "information".

Try s-values instead

Logs are the right scale to think about probability.

Try s-values instead

A p-value of 0.05 is 4.3 bits of information, barely more "surprise" than seeing 4 coin flips that all landed heads.

No more p-value asterisks

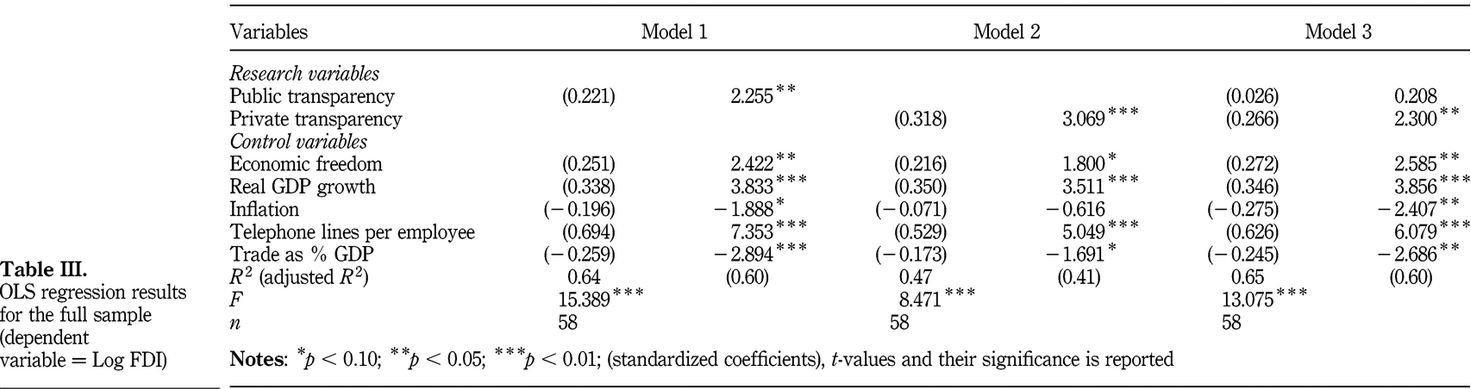
1. Statistical significance isn't a "magnitude"; p=0.045 isn't more significant than p=0.0001.
    
2. It's also moving the goalposts. The original experiment design was for, say, ⍺=0.05. Adding asterisks is claiming "even if we had 0.00x design, we still would have been fine". 

Type I and II errors?

Type I and II errors?

👎

type S error

What is the probability that your point estimate is the wrong sign?

type S error

What is the probability that your point estimate is the wrong sign?

type M error

What is the probability your point estimate is "close" to the correct magnitude (effect size)?

Confidence intervals

[0.97, 1.48]

Risk ratio confidence interval for a serious side effect of an anti-inflammatory drug.

[0.97, 1.48]

Risk ratio confidence interval for a serious side effect of an anti-inflammatory drug.

P-value = 0.091

"Specifically, we recommend that authors describe the practical implications of all values inside the interval, especially the observed effect (or point estimate) and the limits."

"In doing so, they should remember that all the values between the interval’s limits are reasonably compatible with the data, given the statistical assumptions used to compute the interval"

-Greenland, et al, 2018

"Specifically, we recommend that authors describe the practical implications of all values inside the interval, especially the observed effect (or point estimate) and the limits."

"In doing so, they should remember that all the values between the interval’s limits are reasonably compatible with the data, given the statistical assumptions used to compute the interval"

-Greenland, et al, 2018

Testing Framework → Estimation Framework

• accept / reject hypothesis

Testing Framework → Estimation Framework

• accept / reject hypothesis
• p-values as a decision criterion

Testing Framework → Estimation Framework

• accept / reject hypothesis
• p-values as a decision criterion
• type I and type II errors

Testing Framework → Estimation Framework

• accept / reject hypothesis
• p-values as a decision criterion
• type I and type II errors

Testing Framework → Estimation Framework

• accept / reject hypothesis
• p-values as a decision criterion
• type I and type II errors

• looking at estimates & CI and interpreting them

Testing Framework → Estimation Framework

• accept / reject hypothesis
• p-values as a decision criterion
• type I and type II errors

• looking at estimates & CI and interpreting them
• abandoning null hypothesis testing

Testing Framework → Estimation Framework

• accept / reject hypothesis
• p-values as a decision criterion
• type I and type II errors

• looking at estimates & CI and interpreting them
• abandoning null hypothesis testing
• type S and
  type M errors

Testing Framework → Estimation Framework

Twitter ppl to follow

• ProfMattFox
• statsepi
• epiellie
• MaartenvSmeden
• LauraBBalzer
• kaz_yos
• f2harrell

Questions? Comments?

@cmrn_dp