Customer Lifetime Value in Python

Not to be confused with lifelines:

(survival analysis in Python)

Who am I?

• Author of Bayesian Methods for Hackers

• Maintainer of lifelines

• Data analyst here at Shopify

What is Customer Lifetime Value?

According to Google and every business article ever: 

It's the sum of all the earnings you expect to receive from a customer over their lifetime with you.

Why is CLV Important to a company?

1. How much money can I spend per acquisition?
2. Do customers from Twitter or Facebook give me more CLV?
3. What is the net-worth of my company? Should customers be treated as assets on my balance sheet?

Classify Business Settings

1. According to numbers presented in a news release that reported Vodafone Group Plc's results for the six months ended September 2012, Vodafone UK as 10.8 million "pay monthly" customers

2. In his "Q3 2012 Earnings Conference Call", the CFO of Amazon commented that "active customer accounts exceeded 188 million", where customers are considered active when they have placed an order during the preceding twelve-month period.

Which of the following is inaccurate?

Contractual vs Noncontractual settings

Contractual: we observe when the customers dies.

Non-contractual: the time at which a customer dies is unobserved. 

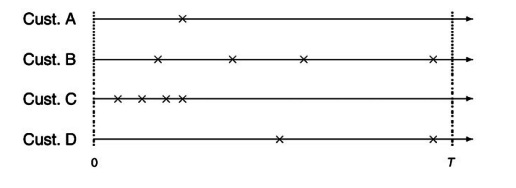
When do we know a customer is still alive?

What are some (bad) formulas for non-contractual CLV?

• m: margin
• r: retention rate
• d: discount factor

Let's create a model of customers

1. Let's assume customers will continuing buying from us until they "die". 

2. Their death rate is constant (but different constants across individuals).

3. Assume exponential time between purchases (with different rates across individuals)

Call this the Pareto model

1. An individual purchases Poisson-ly, with rate  λ, over their lifetime.
2. λ comes from a Gamma(r, α)
3. A customer's lifetime is exponentially distributed, with rate μ.
4. μ comes from a Gamma(s, β)

Pareto/NBD model

What?

1.

2.

3.

4.

Make IPython go now

But we don't know the population parameters! 

Inference

Inference of the population parameter (r, alpha, s, beta) is done using maximum likelihood estimation.

Lifetimes implements this part.

Make IPython go now

Let's create another model of customers.

1. Let's assume customers will continuing buying from us until they "die". 

2. After each additional purchase they have a p-percent chance of dieing (p is unique to the individual).

3. Assume exponential time between purchases.

Call this the BG/NDB model

Make IPython go now.

Also in lifetimes

• test-train splitting for model validation
• more plots
• artificial data simulation functions for validating inference engine, or simulating more data. For example...

Make IPython go now.

Non-business usecases

• Not purchases, but pageviews can be used: a visitor often comes to your site, but hasn't in months - they've probably died.
• Visits to a hospital. We track check-ins, but don't see them "die".
• "Health" of church goers. Did a family lose their faith?
• Any setting where we have have transactions (visits, purchases, check-ins), and underlying death is unobserved. 

Questions?

How does this work for seasonal sales?

Pretty good! Seasonal sales like Christmas are only a blip on the cumulative total number of orders. This might "reawaken" dead customers though, which is not part of our model.

What about Bayesian inference instead of MLE?

Absolutely - this is almost desirable when you are dealing with small businesses who lack lots of data - you want to see the uncertainty in your estimates. 

Dan W. at Pass the ROC does a great job of this: 

http://danielweitzenfeld.github.io/passtheroc/

Ex: instead of point estimates of  λ, I want a distribution of what  λ  might be.