Soss: Lightweight Probabilistic Programming in Julia
Chad Scherrer
November 7, 2019
About Me
Served as Technical Lead for language evaluation for the DARPA program
Probabilistic Programming for Advancing Machine Learning (PPAML)
PPL Publications
-
Scherrer, Diatchki, Erkök, & Sottile, Passage : A Parallel Sampler Generator for Hierarchical Bayesian Modeling, NIPS 2012 Workshop on Probabilistic Programming
-
Scherrer, An Exponential Family Basis for Probabilistic Programming, POPL 2017 Workshop on Probabilistic Programming Semantics
- Westbrook, Scherrer, Collins, and Mertens, GraPPa: Spanning the Expressivity vs. Efficiency Continuum, POPL 2017 Workshop on Probabilistic Programming Semantics
Making Rational Decisions
Managed Uncertainty
Rational Decisions
Bayesian Analysis
Probabilistic Programming
- Physical systems
- Hypothesis testing
- Modeling as simulation
- Medicine
- Finance
- Insurance
Risk
Custom models
Business Applications
Missing Data






The Two-Language Problem
A disconnect between the "user language" and "developer language"
X
3
Python
C
Deep Learning Framework
- Harder for beginner users
- Barrier to entry for developers
- Limits extensibility
?
Introducing Soss
- Simple high-level syntax
- Uses GeneralizedGenerated.jl for flexible staged compilation
- Model type parameter includes type-level representation of itself
- Allows specialized code generation for each primitive(model, data)
A (Very) Simple Example
P(\mu,\sigma|x)\propto P(\mu,\sigma)P(x|\mu,\sigma)
\begin{aligned}
\mu &\sim \text{Normal}(0,5)\\
\sigma &\sim \text{Cauchy}_+(0,3) \\
x_j &\sim \text{Normal}(\mu,\sigma)
\end{aligned}
Theory
Soss
julia> Soss.sourceLogpdf()(m)
quote
_ℓ = 0.0
_ℓ += logpdf(HalfCauchy(3), σ)
_ℓ += logpdf(Normal(0, 5), μ)
_ℓ += logpdf(Normal(μ, σ) |> iid(N), x)
return _ℓ
end@model N begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
x ~ Normal(μ, σ) |> iid(N)
endBuilding a Linear Model
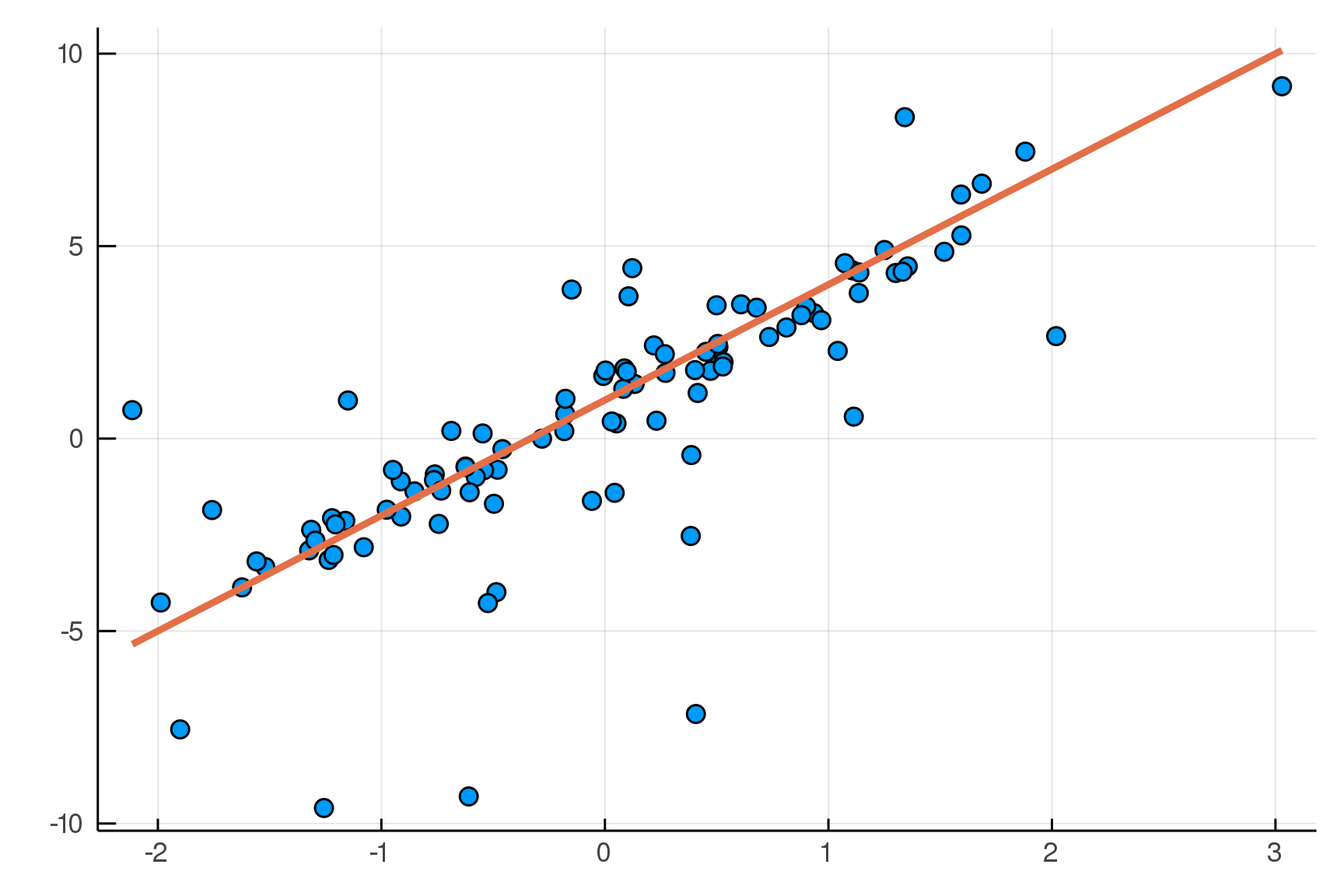
Building a Linear Model
m = @model x begin
α ~ Normal()
β ~ Normal()
σ ~ HalfNormal()
yhat = α .+ β .* x
n = length(x)
y ~ For(n) do j
Normal(yhat[j], σ)
end
endjulia> m(x=truth.x)
Joint Distribution
Bound arguments: [x]
Variables: [σ, β, α, yhat, n, y]
@model x begin
σ ~ HalfNormal()
β ~ Normal()
α ~ Normal()
yhat = α .+ β .* x
n = length(x)
y ~ For(n) do j
Normal(yhat[j], σ)
end
endObserved data is not specified yet!
Sampling from the Posterior Distribution
julia> post = dynamicHMC(m(x=truth.x), (y=truth.y,)) |> particles
(σ = 2.02 ± 0.15, β = 2.99 ± 0.19, α = 0.788 ± 0.2)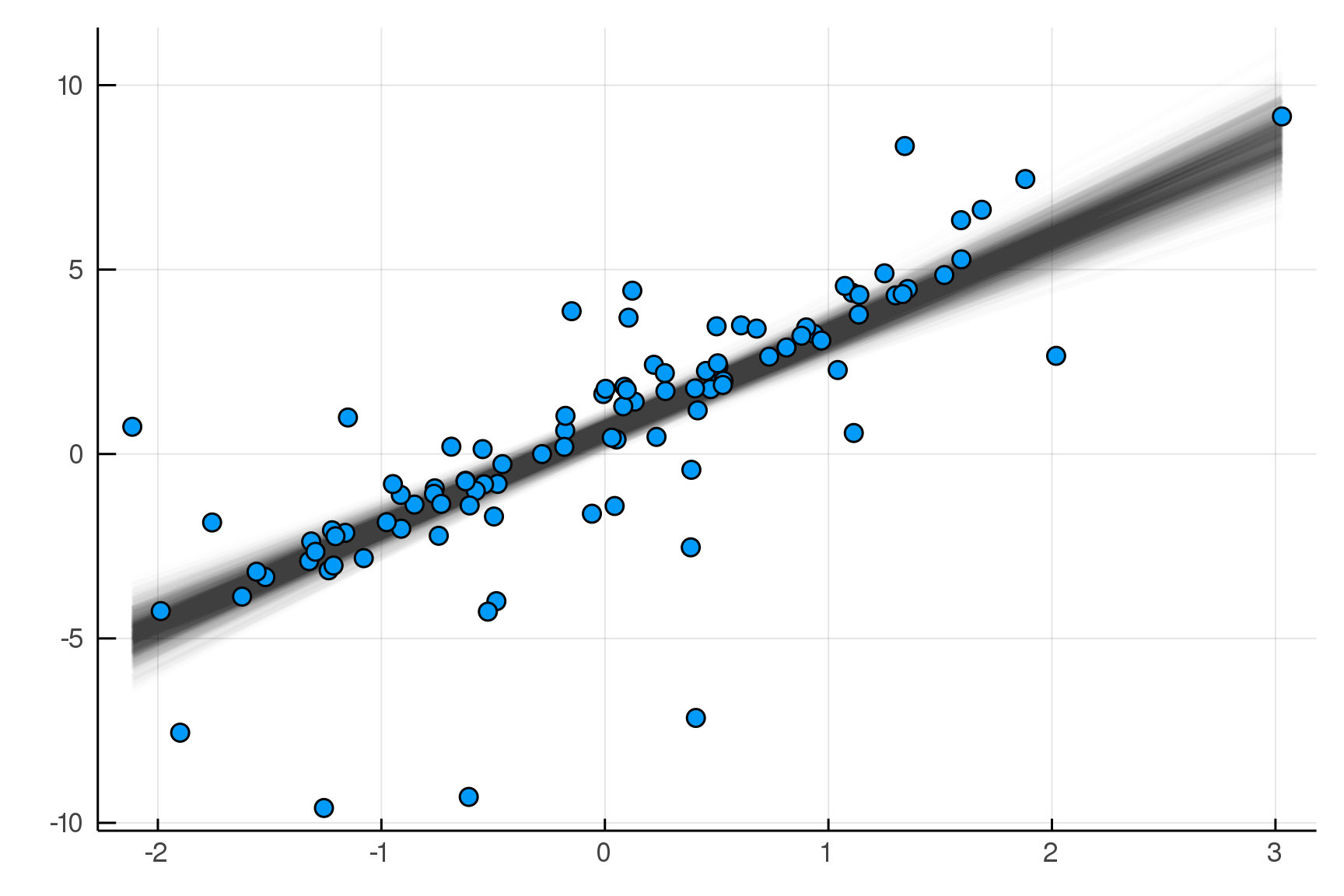
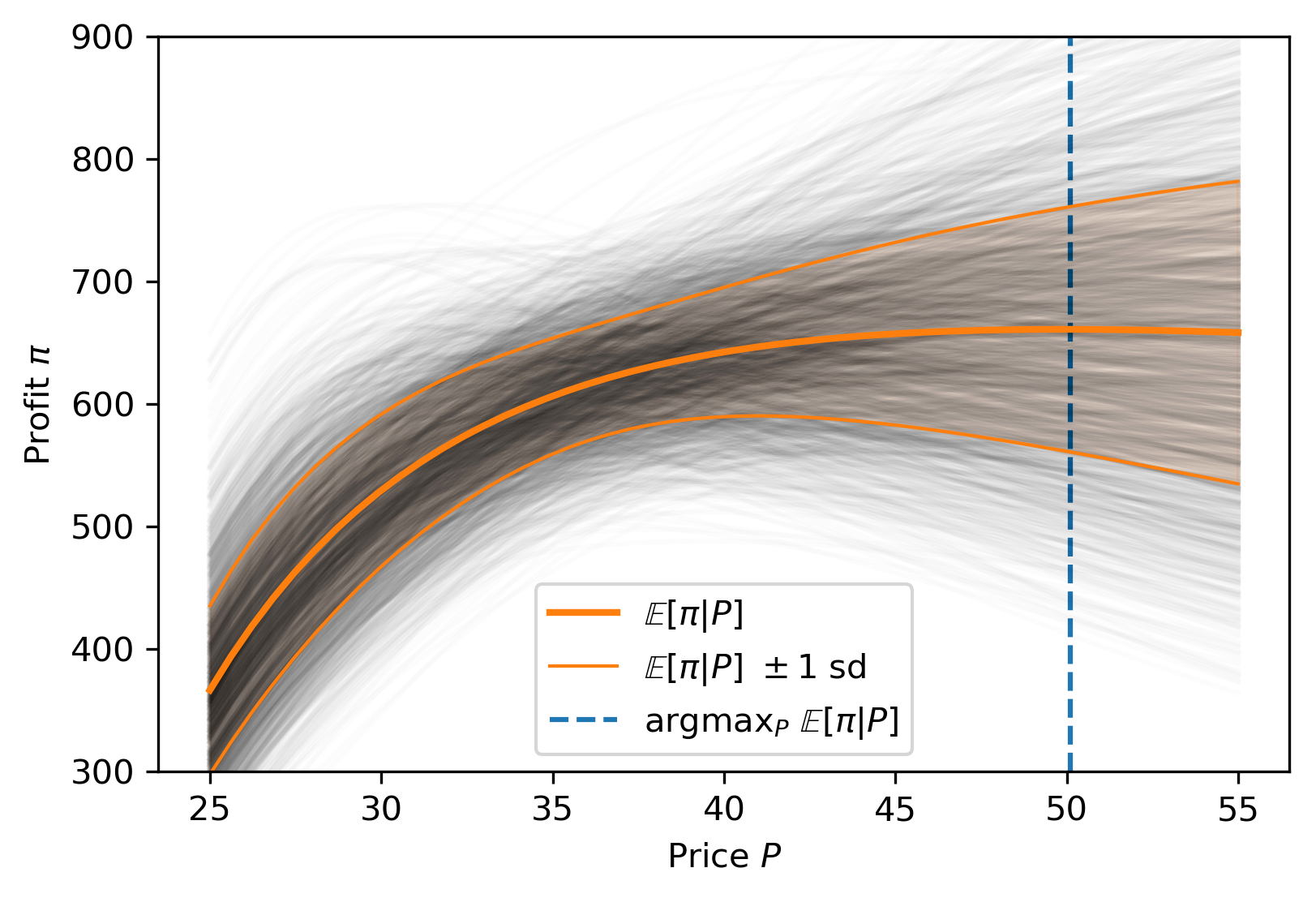
Posterior distribution
Possible best-fit lines
The Posterior Predictive Distribution
Start with Data
Sample Parameters|Data
Sample Data|Parameters
Real Data
Replicated Fake Data
Compare
Posterior
Distribution
Predictive
Distribution
The Posterior Predictive Distribution
pred = predictive(m, :α, :β, :σ)
@model (x, α, β, σ) begin
yhat = α .+ β .* x
n = length(x)
y ~ For(n) do j
Normal(yhat[j], σ)
end
endm = @model x begin
α ~ Normal()
β ~ Normal()
σ ~ HalfNormal()
yhat = α .+ β .* x
n = length(x)
y ~ For(n) do j
Normal(yhat[j], σ)
end
endpostpred = map(post) do θ
delete(rand(pred(θ)((x=x,))), :n, :x)
end |> particlespredictive makes a new model!
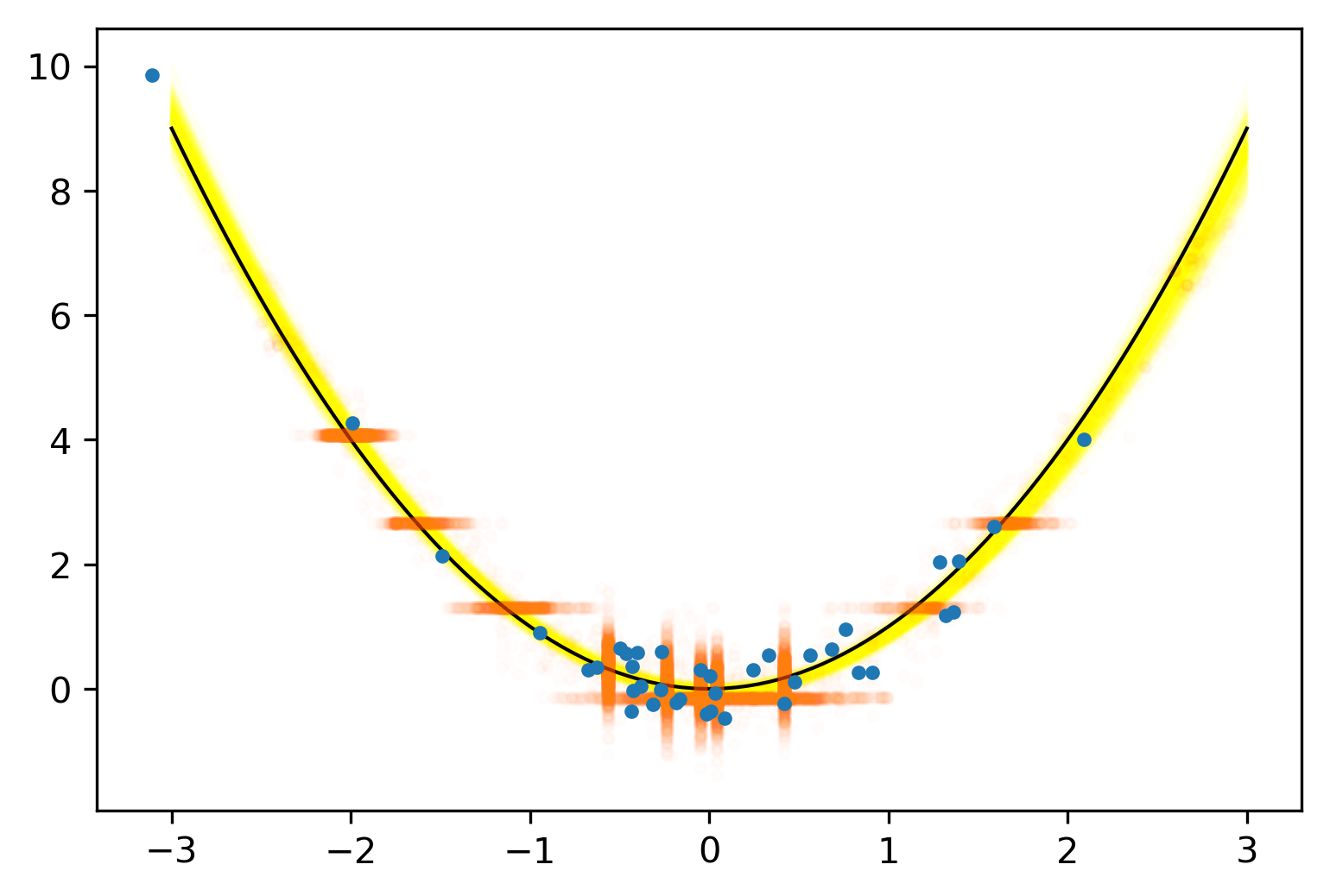
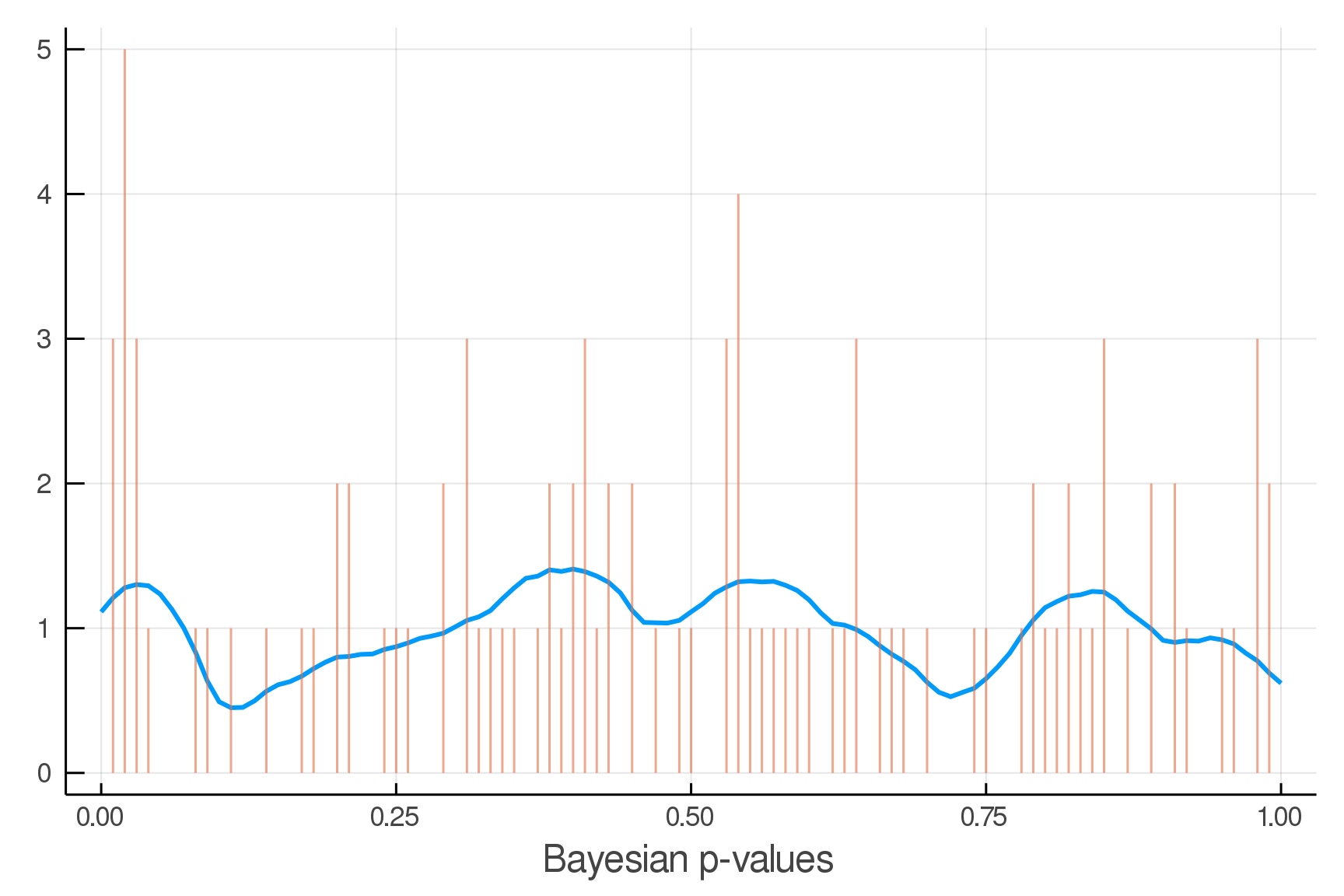
Posterior Predictive Checks
pvals = mean.(truth.y .> postpred.y)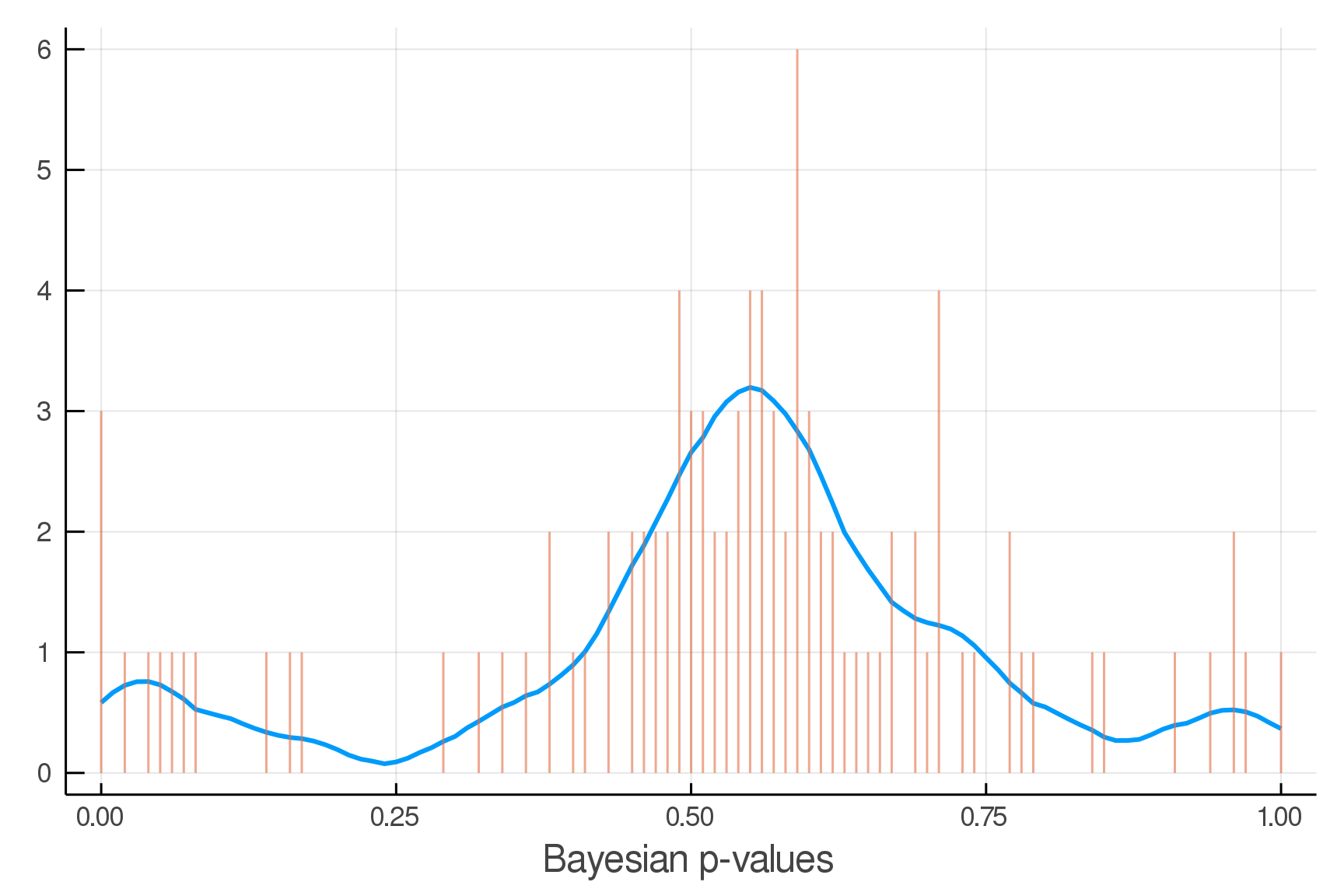
Where we expect the data
Where we see the data
Making it Robust
m2 = @model x begin
α ~ Normal()
β ~ Normal()
σ ~ HalfNormal()
yhat = α .+ β .* x
νinv ~ HalfNormal()
ν = 1/νinv
n = length(x)
y ~ For(n) do j
StudentT(ν,yhat[j],σ)
end
endjulia> post2 = dynamicHMC(m2(x=truth.x), (y=truth.y,)) |> particles
( σ = 0.57 ± 0.09, νinv = 0.609 ± 0.14
, β = 2.73 ± 0.073, α = 0.893 ± 0.077)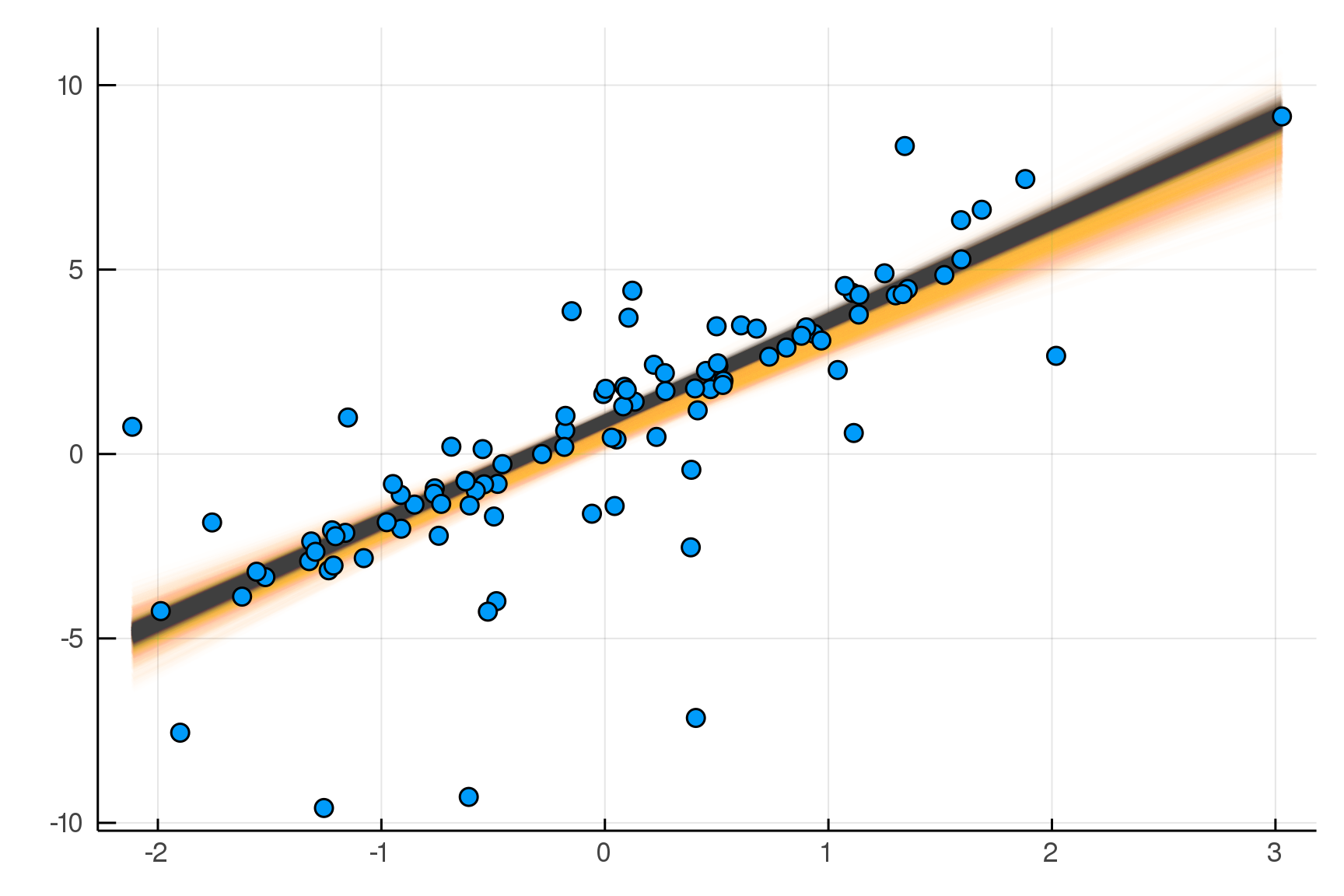
Updated Posterior Predictive Checks
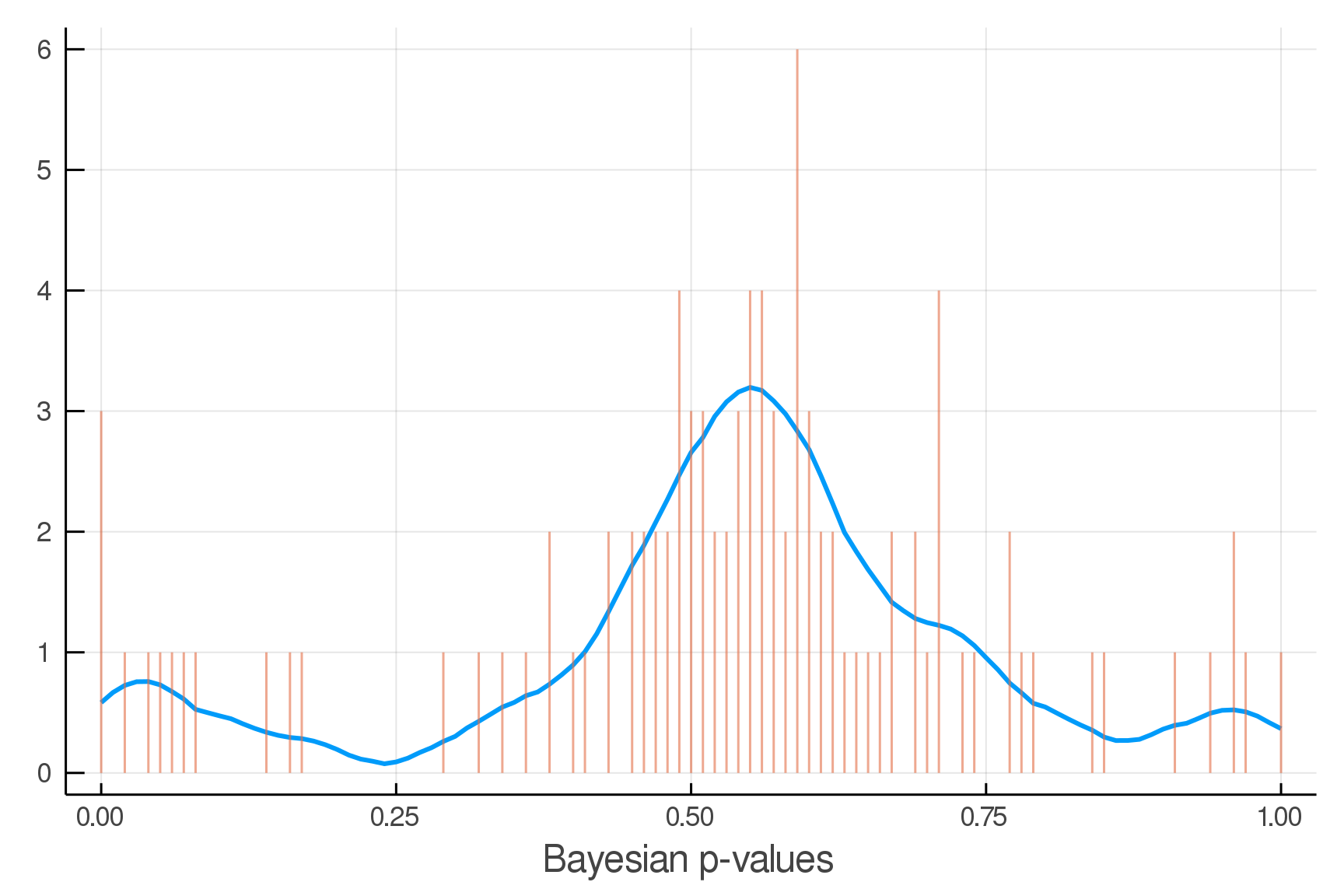
Inference Primitive: rand
julia> Soss.sourceRand()(m)
quote
σ = rand(HalfNormal())
β = rand(Normal())
α = rand(Normal())
yhat = α .+ β .* x
n = length(x)
y = rand(For(((j,)->begin
Normal(yhat[j], σ)
end), n))
(x = x, yhat = yhat, n = n
, α = α, β = β, σ = σ, y = y)
end@model x begin
σ ~ HalfNormal()
β ~ Normal()
α ~ Normal()
yhat = α .+ β .* x
n = length(x)
y ~ For(n) do j
Normal(yhat[j], σ)
end
endInference Primitive: logpdf
julia> Soss.sourceLogpdf()(m)
quote
_ℓ = 0.0
_ℓ += logpdf(HalfNormal(), σ)
_ℓ += logpdf(Normal(), β)
_ℓ += logpdf(Normal(), α)
yhat = α .+ β .* x
n = length(x)
_ℓ += logpdf(For(n) do j
Normal(yhat[j], σ)
end, y)
return _ℓ
end@model x begin
σ ~ HalfNormal()
β ~ Normal()
α ~ Normal()
yhat = α .+ β .* x
n = length(x)
y ~ For(n) do j
Normal(yhat[j], σ)
end
endInference Primitive: symlogpdf
julia> Soss.sourceSymlogpdf()(m)
quote
_ℓ = 0.0
x = sympy.IndexedBase(:x)
yhat = sympy.IndexedBase(:yhat)
n = sympy.IndexedBase(:n)
α = sympy.IndexedBase(:α)
β = sympy.IndexedBase(:β)
σ = sympy.IndexedBase(:σ)
y = sympy.IndexedBase(:y)
_ℓ += symlogpdf(HalfNormal(), σ)
_ℓ += symlogpdf(Normal(), β)
_ℓ += symlogpdf(Normal(), α)
yhat = sympy.IndexedBase(:yhat)
n = sympy.IndexedBase(:n)
_ℓ += symlogpdf(For(n) do j
Normal(yhat[j], σ)
end, y)
return _ℓ
end@model x begin
σ ~ HalfNormal()
β ~ Normal()
α ~ Normal()
yhat = α .+ β .* x
n = length(x)
y ~ For(n) do j
Normal(yhat[j], σ)
end
endSymbolic Simplification
julia> symlogpdf(m)julia> symlogpdf(m) |> expandSums-3.7-0.5α^{2}-0.5β^{2}-σ^{2}+\sum_{j_{1}=1}^{n}\left(-0.92-\logσ-\frac{0.5\left(y_{j_{1}}-\hat{y}_{j_{1}}\right)^{2}}{σ^{2}}\right)
-3.7-0.5α^{2}-0.5β^{2}-σ^{2}-0.92n-n\logσ-\frac{0.5}{\sigma^{2}}\sum_{j_{1}=1}^{n}\left(y_{j_{1}}-\hat{y}_{j_{1}}\right)^{2}
Code Generation
julia> symlogpdf(m()) |> expandSums |> foldConstants |> codegen
quote
var"##add#643" = 0.0
var"##add#643" += -3.6757541328186907
var"##add#643" += begin
var"##mul#644" = 1.0
var"##mul#644" *= -0.5
var"##mul#644" *= begin
var"##arg1#646" = α
var"##arg2#647" = 2
var"##symfunc#645" = (Soss._pow)(var"##arg1#646", var"##arg2#647")
var"##symfunc#645"
end
var"##mul#644"
end
var"##add#643" += begin
var"##mul#648" = 1.0
var"##mul#648" *= -0.5
var"##mul#648" *= begin
var"##arg1#650" = β
var"##arg2#651" = 2
var"##symfunc#649" = (Soss._pow)(var"##arg1#650", var"##arg2#651")
var"##symfunc#649"
end
var"##mul#648"
end
var"##add#643" += begin
var"##mul#652" = 1.0
var"##mul#652" *= -1.0
var"##mul#652" *= begin
var"##arg1#654" = σ
var"##arg2#655" = 2
var"##symfunc#653" = (Soss._pow)(var"##arg1#654", var"##arg2#655")
var"##symfunc#653"
end
var"##mul#652"
end
var"##add#643" += begin
var"##mul#656" = 1.0
var"##mul#656" *= -0.9189385332046727
var"##mul#656" *= n
var"##mul#656"
end
var"##add#643" += begin
var"##mul#657" = 1.0
var"##mul#657" *= -0.5
var"##mul#657" *= begin
var"##arg1#659" = σ
var"##arg2#660" = -2
var"##symfunc#658" = (Soss._pow)(var"##arg1#659", var"##arg2#660")
var"##symfunc#658"
end
var"##mul#657" *= begin
let
var"##sum#661" = 0.0
begin
var"##lo#663" = 1
var"##hi#664" = n
@inbounds for _j1 = var"##lo#663":var"##hi#664"
begin
var"##Δsum#662" = begin
var"##arg1#666" = begin
var"##add#668" = 0.0
var"##add#668" += begin
var"##mul#669" = 1.0
var"##mul#669" *= -1.0
var"##mul#669" *= begin
var"##arg1#671" = yhat
var"##arg2#672" = _j1
var"##symfunc#670" = (getindex)(var"##arg1#671", var"##arg2#672")
var"##symfunc#670"
end
var"##mul#669"
end
var"##add#668" += begin
var"##arg1#674" = y
var"##arg2#675" = _j1
var"##symfunc#673" = (getindex)(var"##arg1#674", var"##arg2#675")
var"##symfunc#673"
end
var"##add#668"
end
var"##arg2#667" = 2
var"##symfunc#665" = (Soss._pow)(var"##arg1#666", var"##arg2#667")
var"##symfunc#665"
end
var"##sum#661" += var"##Δsum#662"
end
end
end
var"##sum#661"
end
end
var"##mul#657"
end
var"##add#643" += begin
var"##mul#676" = 1.0
var"##mul#676" *= -1.0
var"##mul#676" *= n
var"##mul#676" *= begin
var"##arg1#678" = σ
var"##symfunc#677" = (log)(var"##arg1#678")
var"##symfunc#677"
end
var"##mul#676"
end
var"##add#643"
endjulia> @btime logpdf($m(x=x), $truth)
1.911 μs (25 allocations: 1.42 KiB)
-901.7607073245318julia> @btime logpdf($m(x=x), $truth, codegen)
144.671 ns (1 allocation: 896 bytes)
-903.4977930382969Default
Code Generation
- New feature, still in development
- Speedup depends on lots of things
First-Class Models
julia> m = @model begin
a ~ @model begin
x ~ Normal()
end
end;
julia> rand(m())
(a = (x = -0.20051706307697828,),)julia> m2 = @model anotherModel begin
y ~ anotherModel
z ~ anotherModel
w ~ Normal(y.a.x / z.a.x, 1)
end;
julia> rand(m2(anotherModel=m)).w
-1.822683102320004Coming Soon
- Stream combinators via Transducers.jl and OnlineStats.jl
- Connection to other PPLs: Turing.jl, Gen.jl
- Normalizing flows with Bijectors.jl
- Deep learning with Flux.jl
- Gaussian processes
Thank You!

Special Thanks for
2019-11-07-Soss
By Chad Scherrer
2019-11-07-Soss
- 1,247



