cvanelteren
Computational scientist
Information flows in criminal networks
University of Amsterdam
Casper van Elteren
Education
- Cognitive neuroscience, cum laude
- Brain networks and neuronal communication
- Psychobiology, cum laude
- Minor computational science
Skills
Achievements
- Informational toolbox
- Zebrafish viewer
- Brain computer interface
- Woningnet automization
- Best in class BSc
Data visualization
Writing
Python
C++
Critical
Analytical
Creativity
Hobbies
Interests
- Causal inference
- Information theory
- Complexity science
Math
Understanding the process
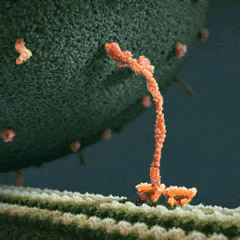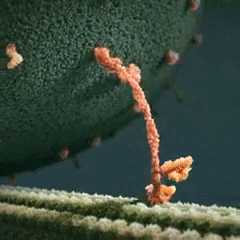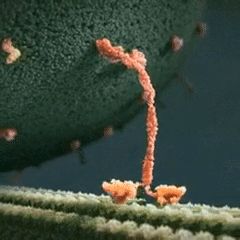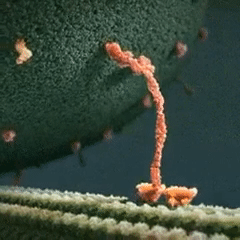
Transient dynamics:
Closing the gap between consciousness and sub-consciousness
2012
Frequency sliding: novel non-linear approach to EEG analysis
Top-down modulation of the hollow mask illusion
2013
Intelligence as Dynamic Property in WAIS-III
The Hard Problem of Consciousness: A Metaphysical Remedy for Neurophenomenology
2016
2019
The dynamic importance of nodes is poorly predicted by static topological features
Why heuristics don't work
Agent modeling
Mouse simulation in Morris water maze using temporal difference learning
Big Data
Information Impact
Large-scale pattern recognition whole brain data of the Zebrafish
Detecting driver-nodes in complex systems using information theory
Computational framework
High performance general graph-based
The dynamic importance of nodes is poorly predicted by static topological features
Does structural connectedness translate to dynamical importance?
\dot x = M_0 (x_i) + \sum_i^N A_{ij} M_1(x_i) M_2(x_j)
+
+
Which feature is considered important?
How to compare different models?
Harush et al. (2017)
Information theory and complex systems
- Quantify uncertainty of random variables
- Universal language
- Mechanism independent
- Strips semantics from syntax (Quax 2016)
- Non-linear description possible
H(X) = - \sum_{x \in X} P(x) \log P(x)
\begin{aligned}
I(X : Y) &= \sum_{x \in X y \in Y} P(x, y) \log \frac{P(x,y)}{P(x)P(y)}\\
&= H(X) - H(X | Y)\\
&= H(Y) - H(Y | X)\\
\end{aligned}
Entropy
Mutual information
Shannon (1948)
Diminishing role of hubs
Quax et al. (2013)
- Infinitely sized networks
- Locally tree-like
- No-self loops
Degree
Numerical
Analytical
d(s_i) = \{t : I(s_i^{t_0 + t} : S^{t_0}) = \frac{1}{2} H(s_i) \}
Informational impact
- Node with largest causal influence has highest information impact
- Observations only!
- No interventions required
\mu_i := \sum_{t=0}^\infty I(s_i^{t_0 + t} : S^{t_0}) \Delta t
Informational impact
Betweenness
Degree
Current flow
Eigenvector
Low intervention
High intervention
- No structural metric showed a linear relation with low causal impact
- Information impact was highly linear with low causal impact
Text
- Something about criminal networks
Causal inference
- Look at the available data(!)
- Expert knowledge
- Obtaining causal model
- Forward modelling
- Causal state reconstruction
- Epsilon machines
- Obtaining correct level of description using information theory
Ideas
Thank you!
Information in complex systems
Given ergodic system S
Information will always decrease as function of time
Driver-node will share the most information with the system over time
Agent modeling
- Distal reward problem;
- Global consistency problem.
\delta_t = R_t + \gamma C_{t+1}(p) - C_t(p)
Foster et al. (2000)
How do place cells encode location?
Computational gap bridged by temporal distance learning (Sutton, 1988)
Agent modeling
Foster et al. (2000)
- Underwhelming does not match overwhelming causal impact
- Information impact matches underwhelming causal impact
Fried at al. (2015)
Information impact captures driver-node change
Zebrafish viewer
Ahrens et al. (2013)
Opportunities
- Interdisciplinary research
- Advance mathematical skills
Threats
- Get stuck on topic too long
- Integration of information
Weakness
- Mathematical rigor
Strengths
- Critical
- Analytical
- Excellent programmer
Information impact varies linearly with low causal impact
Informational impact on criminal networks
By cvanelteren
Informational impact on criminal networks
Criminal networks at UvA
