Algorithm Analysis:

 

Asymptotic Complexity

Agenda

  • Prerequisites
  • Why is the Analysis of Algorithms important?
  • What's the goal of Asymptotic Complexity?
  • What are we really measuring?
    • RAM computational model
  • Machine Operations as a Function
  • Asymptotic Complexity
  • Asymptotic Notation (Θ, O, Ω)

Prerequisites

  • Basic Programming
  • Basic Algebra
  • Mathematical Functions
  • Graphing
  • Logarithms
  • Set Notation (helpful)

Why is the Analysis of Algorithms Important?

  • Foundational concept for computation
  • Design performant algorithms
    • Understand language primitives
  • Develop an intuition for scale
  • Identify intractable problems
  • Learn patterns and techniques from the "greatest hits" of programming
  • Poorly taught in academia
    • Impetus for my book (https://hideoushumpbackfreak.com/algorithms/)

Litmus Test

If you think you don't need it, or you know it and never use it, you most likely need to study it.

What's the Goal of Asymptotic Complexity?

  • Performance-centric analysis (sort of...)
  • Why not measure clock time?
    • Machine variation
    • Input size must be a factor
  • Concisely express how an algorithm will scale without regard to a particular physical machine
  • Simple means for comparing algorithms
    • "[Asymptotic Complexity] significantly simplifies calculations because it allows us to be sloppy – but in a satisfactorily controlled way" - Donald Knuth
  • Theoretical framework for advanced algorithm analysis

What are we measuring?

  • Approximate number of Machine Operations​
  • It's not practical to measure the actual number of machine operations
    • Programming language variations
    • Machine variations
    • Parallelism
  • Radom Access Machine (RAM) Model
    • Not to be confused with Random Access Memory

Random Access Machine (RAM)

  • Theoretical computing machine
    • Algorithm Comparisons independent of a physical machine
    • Runs pseudo code
  • Assumptions
    • Sequential execution of instructions
    • Fixed word sizes
    • Standard integer and floating-point numbers
  • ​Operations​ (loosely defined)
    • Arithmetic (add, subtract, multiply, divide, remainder, floor, ceiling)
    • Data Movement (load, store, copy)
    • Control (conditional branch, unconditional branch, subroutine call, return)

RAM Operations

1 data operation

1 control operation X 3 iterations

1 arithmetic and 1 data operation X 3 iterations

1 control operation

Total = 12 operations

If we are being pedantic, this is how to count operations...

1 control operation

j ← 0

for i∈{1,2,3} do
   j←i × 2
end for

return j

RAM Operations

  • An operation is roughly equivalent to an executed line of pseudo code
  • It's acceptable to take reasonable liberties

\( d \gets \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)

1 operation

1 operation X 3 iterations

1 operation X 3 iterations

1 operation

ignore

1 operation

How do machine operations relate to scale?

j ← 0

for i∈{1,2,3} do
   j←i × 2
end for

return j

Total = 8 operations

Machine Operations as a \( f(x) \)

  • When considering scale, growth rate in relation to input size is what's important
  • Mathematical function describing the relationship between operations and input size
  • Input Size
    • Could be anything: number of bits, a scalar value,  etc...
    • Typically number of items:  elements in array, nodes in graph, etc...
  • Conventions
    • Input size = \( n \)
    • Growth rate function = \( T(n) \) 

\( T(n) \) Example

function square(A)
   for i ← 0 to |A| −1 do
      A[i] = A[i] x A[i]
   endfor
end function

1 operation per item

1 operation per item

Total = 2 operations per item

\( T(n) = 2n \)

More Complex \( T(n) \)

  • Not all algorithms can be expressed by a single \( T(n) \)
    • Upper Bound
    • Lower Bound
function findDuplicates(A)
   D←∅
   for i←0 to |A| −1 do
      for j←0 to |A| −1 do
         if i≠j and A[i] = A[j] then
            D←D ∪ {A[i]}
         end if
      end for
   end for
   return D
end function

1 operation

\( n \) operations

\( n^2 \) operations (\( n \) per item)

\( n^2 \) operations (\( n \) per item)

Between 0 and \( n^2 \) operations

1 operation

T(n)=1+n+n^2+n^2+n^2+1 \\ T(n)=3n^2+n+2

Upper Bound

T(n)=1+n+n^2+n^2+0+1 \\ T(n)=2n^2+n+2

Lower Bound

Comparing \( T(n) \)

Under reasonable assumptions, square scales much better than findDuplicates

Asymptotic Complexity

Review: The goal is to concisely express how an algorithm will scale​ (growth rate)

Loosely consider the asymptotic complexity to be the "shape" of \( T(n) \)

Deriving Asymptotic Complexity

Remove all constants and non-leading terms

T(n)=3n^2+n+2

Constants

Non-Leading Term

T(n)=n^2

The "shape" does not change

6 Basic Complexity Classes

Name Growth Rate Example
Constant Hash Table (Look up)
Logarithmic Binary Tree (Search)
Linear Linked List (Search)
Quadratic Bubble Sort
Exponential Traveling Salesman (Dynamic Programming)
Factorial Traveling Salesman (Brute Force)
T(n) = 1
T(n) = \log_2{n}
T(n) = n
T(n) = n^2
T(n) = 2^n
T(n) = n!

Asymptotic Complexity Shapes

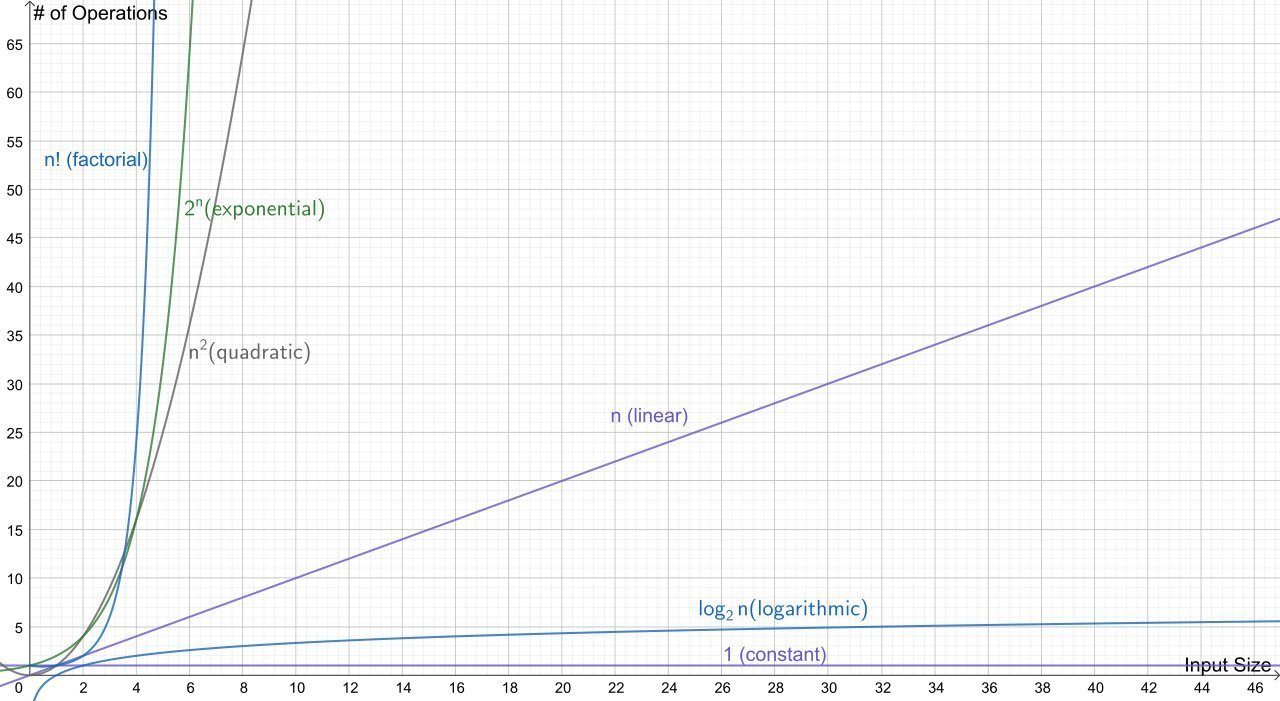
What does Asymptotic Complexity Really Say?

  • Larger asymptotic complexity values equate to longer run times given that the input size is sufficiently large.
  • Consider two theoretical algorithms
    • \( \sigma - T(n) = n^2 \) - asymptotically quadratic
    • \( \alpha - T(n) = 50n \) - asymptotically linear

Question: Does the linear algorithm always execute fewer machine operations?

What does Asymptotic Complexity Really Say?

Answer: No, for values of \( n \) lower than 50, \( \sigma \) has fewer operations that \( \alpha \)

Asymptotic Complexity

One Last Time:

The goal is to concisely express how an algorithm will scale​ (growth rate)

Asymptotic Notation

  • Known as Landau Symbols outside of CS
  • Express asymptotic concepts concisely
    • \( \Theta \) - Big Theta
    • \( O \) - Big O
    • \( \Omega \) - Big Omega

\( \Theta \) - Big Theta

  • Asymptotic Tight Bound
    • Asymptotic complexity is the same regardless of input
  • It’s not possible to specify \( \Theta \) for all algorithms
  • Recall findDuplicates
    • ​Lower Bound \( T(n) = 3n^2+n+2 \)
    • Upper Bound \( T(n) = 2n^2+n+2 \)
  • ​Asymptotic complexity for upper and lower is \( T(n) = n^2 \)
  • findDuplicates = \( \Theta(n^2) \)

\( O \) - Big O

  • Asymptotic Upper Bound
    • Worst Case Scenario 
  • O stands for Order of or more precisely the German word Ordnung
  • \( \Theta \) is a stronger statement than \( O \)
    • if findDuplicates = \( \Theta(n^2) \) then findDuplicates = \( O(n^2) \)
    • Big O makes no indication of the best case scenario

\( \Omega \) - Big Omega

  • Asymptotic Lower Bound
    • Best Case Scenario 
  • \( \Theta \) is a stronger statement than \( \Omega \)
    • if findDuplicates = \( \Theta(n^2) \) then findDuplicates = \( \Omega(n^2) \)
    • Big \( \Omega \) makes no indication of the worst case scenario

Example Analysis

function bubbleSort(A)
   sorted ← false
   index ← |A| − 2
   while sorted is false do
      sorted←true
      for i ← to index do
         if A[i] > A[i + 1] then
            swap A[i] and A[i + 1]
            sorted ← false
         end if
      end for
      index ← index - 1
   end while
end function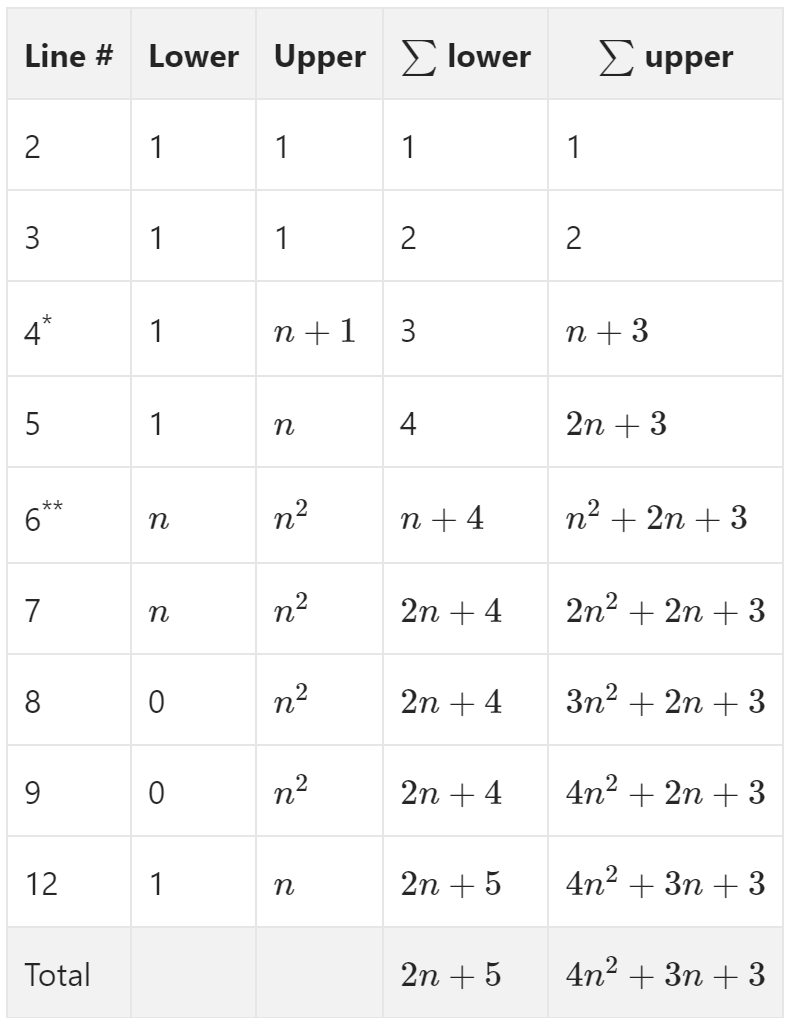

Lower \( 2n + 5 \)               \( \Omega(n) \)

Upper \( 4n^2 + 3n + 3 \)    \( O(n^2) \)

* Continues to loop until the for loop on line 6 makes a complete revolution without triggering the if statement on line 7. The extra operation is the exit condition (sorted is true)
** The number of iterations is reduced by 1 for each iteration of the outer loop by virtue of line 12. So it’s technically \( \sum_{i=1}^{n} i \) ; however, this is a bit of minutia that’s best left rounded up to \( n^2 \).

Thank You!

  • If you liked this content, let me know and I'll make more
  • If you hated this content, let me know and I'll do better

Asymptotic Complexity

By Dale Alleshouse

Made with Slides.com

Asymptotic Complexity

  • 1,169

More from Dale Alleshouse