Plasticity & Shear bands
- a quick overview of past results
- constitutive models
- underworld results
- future directions

Plasticity & Shear bands
Spiegelman, Marc, Dave A. May, and Cian R. Wilson. "On the solvability of incompressible Stokes with viscoplastic rheologies in geodynamics." Geochemistry, Geophysics, Geosystems 17.6 (2016): 2213-2238.
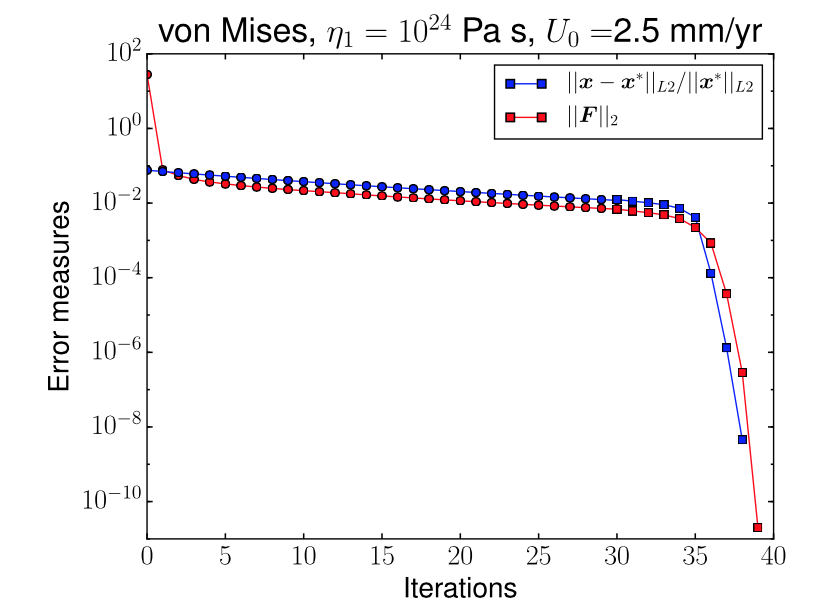
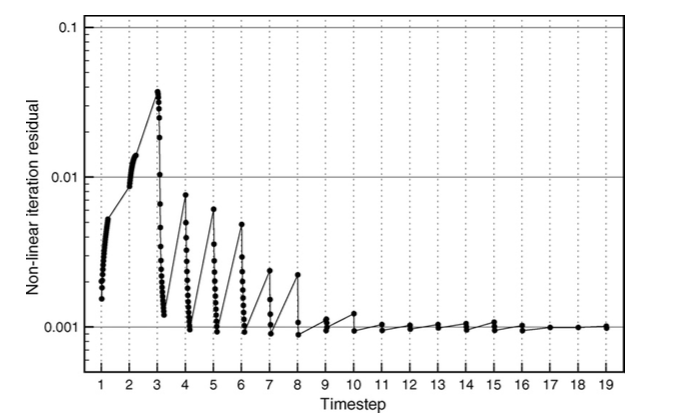
- Newton's method can substantially reduce the residual compared to point iterations
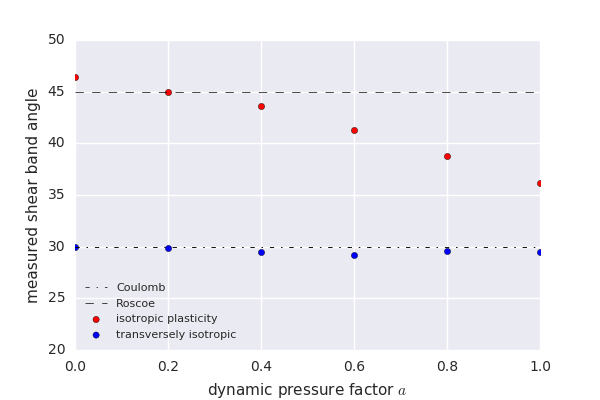
- macroscopic Shear band angle has little dependence on the angle of internal friction
- Drucker-Prager model won't converge if pressure-sensitivity of deviatoric stress is too -high,
- problems that arise from combining dynamic pressure-dependent rheologies with incompressible Stokes where the dynamic pressure enforces the incompressibility constraint.
- a quick overview of past results
Plasticity & Shear bands
Kaus, Boris JP. "Factors that control the angle of shear bands in geodynamic numerical models of brittle deformation." Tectonophysics 484.1 (2010): 36-47.
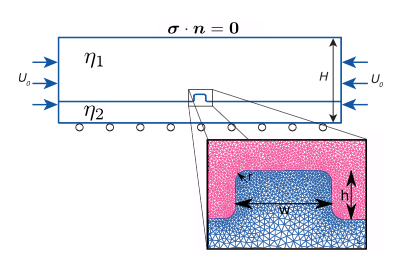
- Coulomb orientation only occurs if the heterogeneity, which induces this shear band, is resolved with a sufficiently large numerical resolution.
- a quick overview of past results
Plasticity & Shear bands
Lemiale, V., et al. "Shear banding analysis of plastic models formulated for incompressible viscous flows." Physics of the Earth and Planetary Interiors 171.1 (2008): 177-186.
APA
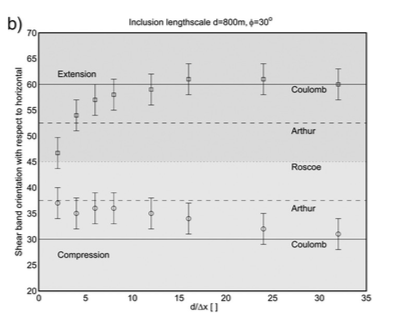
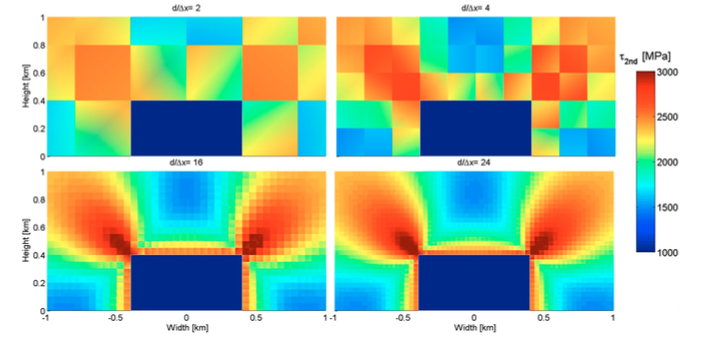
- It is found that the so-called Roscoe solution and Coulomb solution are both admissible solutions for the Drucker-Prager model
- mesh must be sufficiently refined in order to capture the Coulomb orientation numerically.
- use of a viscous layer underneath causes the localization to be less pronounced than in the present work, making the strain rate invariant field somewhat more diffuse
- a quick overview of past results
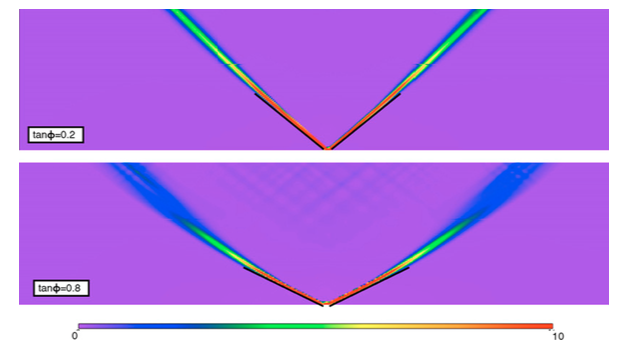
Plasticity & Shear bands
- Drucker-Prager model:
- constitutive models
\tau_{II} \leq A + B (P_{lith} + \alpha(P')) \leq Y
τII≤A+B(Plith+α(P′))≤Y
\tau_{II} = \sqrt{\frac{1}{2}\tau_{ij}:\tau_{ij} }
τII=√21τij:τij
\tau_{ij} = 2\eta\epsilon_{ij} = \eta[\nabla u + \nabla u^T]
τij=2ηϵij=η[∇u+∇uT]
Plasticity & Shear bands
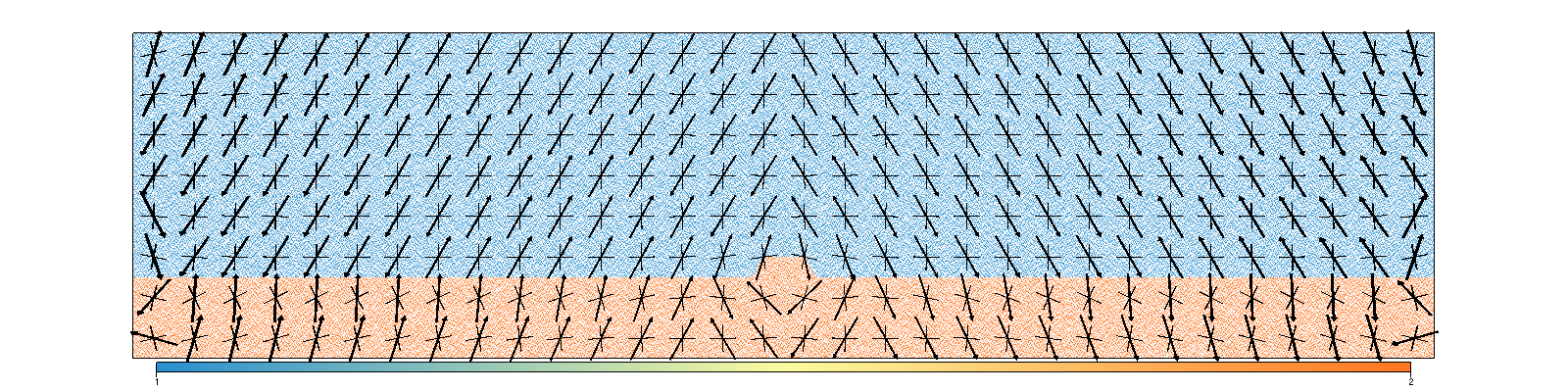
- Mohr-Coulomb model (Underworld2 implementation):
- constitutive models
\tau_{s} \leq tan( \phi) \sigma_n + C
τs≤tan(ϕ)σn+C
\tau_{ij} = 2\eta\dot \epsilon_{ij} - 2(\eta-\eta_s) \Lambda_{ijlm} \dot \epsilon_{ij}
τij=2ηϵ˙ij−2(η−ηs)Λijlmϵ˙ij
2\eta_s = \frac{\tan \phi (2\eta n_k n_l \dot \epsilon_{kl} - p) + c}{\dot \gamma}
2ηs=γ˙tanϕ(2ηnknlϵ˙kl−p)+c
\dot \gamma = n_i \dot \epsilon_{ij}s_j
γ˙=niϵ˙ijsj
Plasticity & Shear bands
- Mohr-Coulomb model (Underworld2 implementation):
- constitutive models
\tau_{s} \leq tan( \phi) \sigma_n + C
τs≤tan(ϕ)σn+C
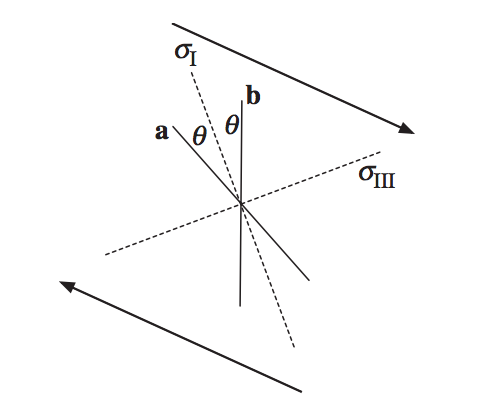
\dot n_i = L_{ji} n_j
n˙i=Ljinj
- Choose the slip plane that maximises:
Plasticity & Shear bands
- Drucker-Prager model
- Isotropic
- Coaxial?
- How do macroscopic shear bands 'know' what angle to form at?
- Coulomb angle results in the fastest rate of pressure reduction within the shear band
- constitutive models
\pm \left( \frac{\pi}{4} + \frac{\phi}{2} \right)
±(4π+2ϕ)
Plasticity & Shear bands
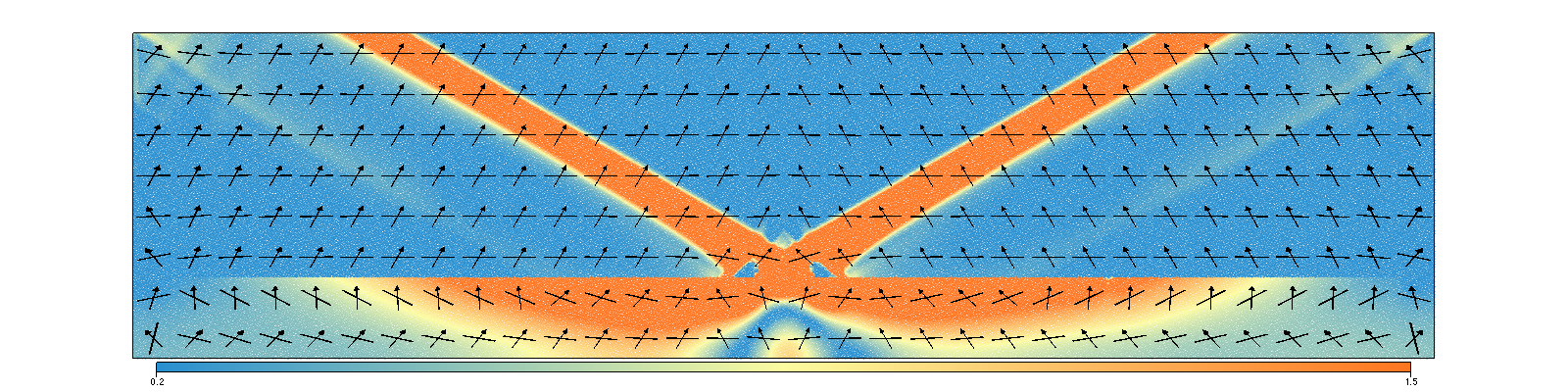
- underworld2 - Drucker Prager
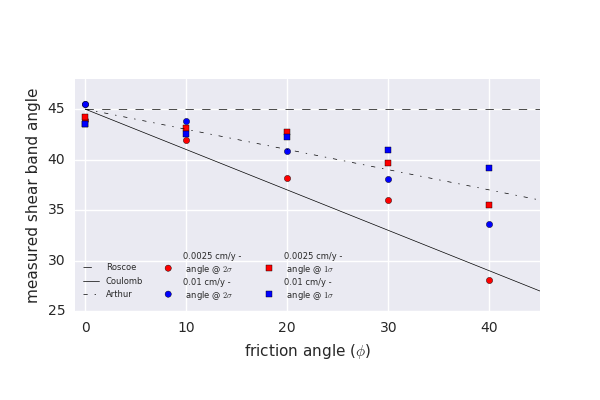
- Questions:
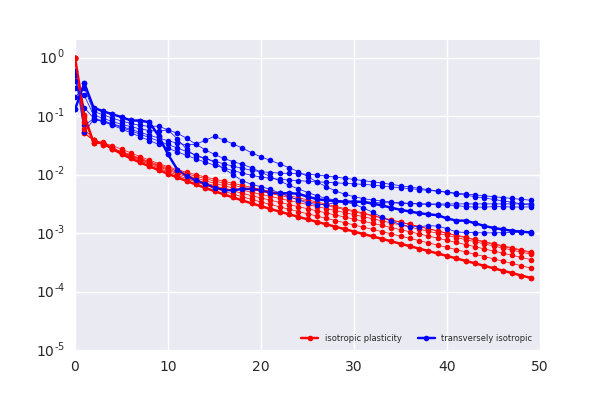
- what is the convergence behaviour transversely isotropic model?
- Can pseudo-compressibility help smooth the dynamic pressure?
- Is a Newton scheme required?
Plasticity & Shear bands
- underworld2 - Drucker Prager
- Questions:
- Is a Newton scheme required?
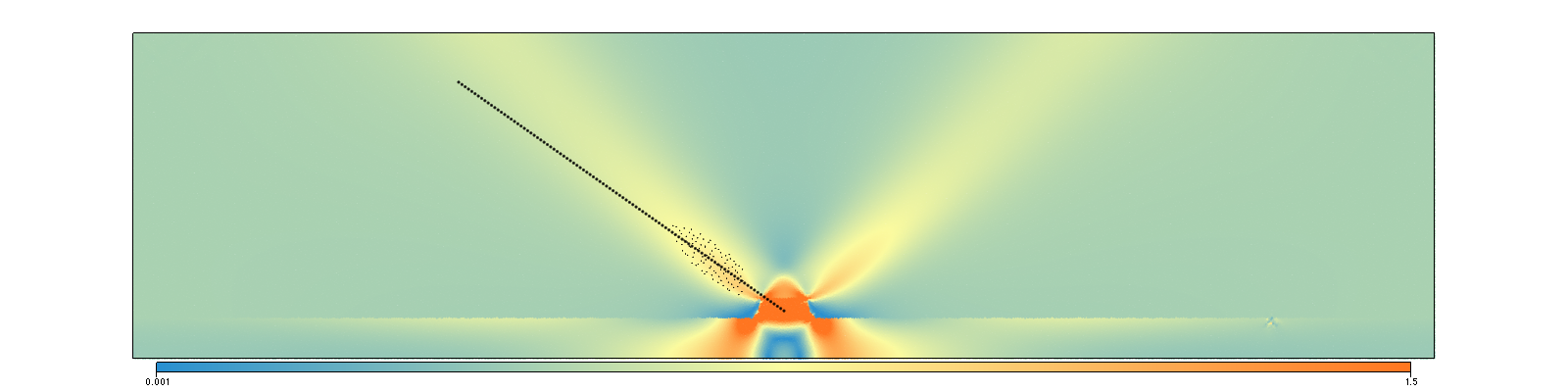
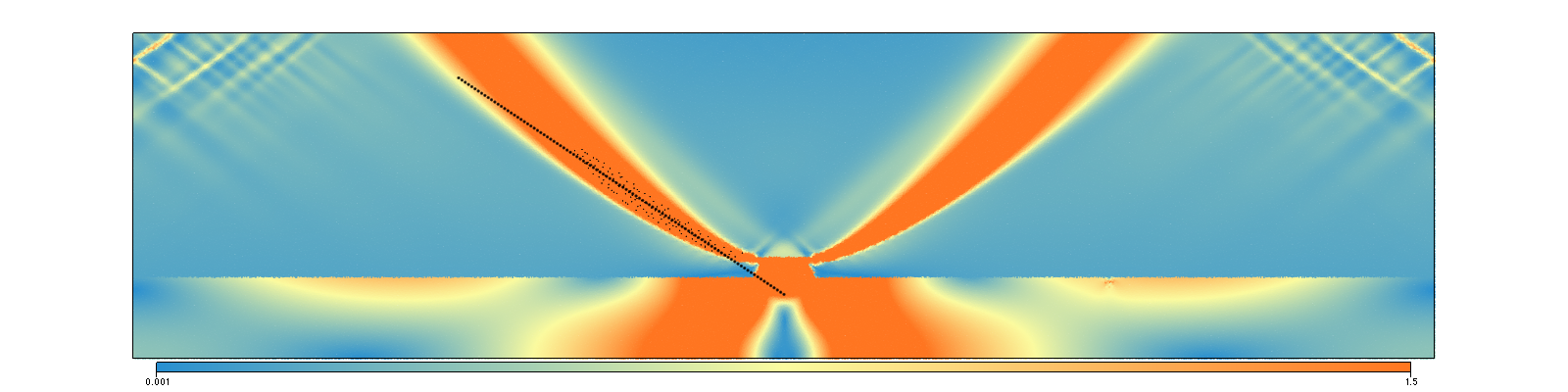
Plasticity & Shear bands
- underworld2 - Drucker Prager
\tau_{II} \leq A + B (P_{lith} + \alpha(P')) \leq Y
τII≤A+B(Plith+α(P′))≤Y
- Questions:
- what is the convergence behaviour transversely isotropic model?
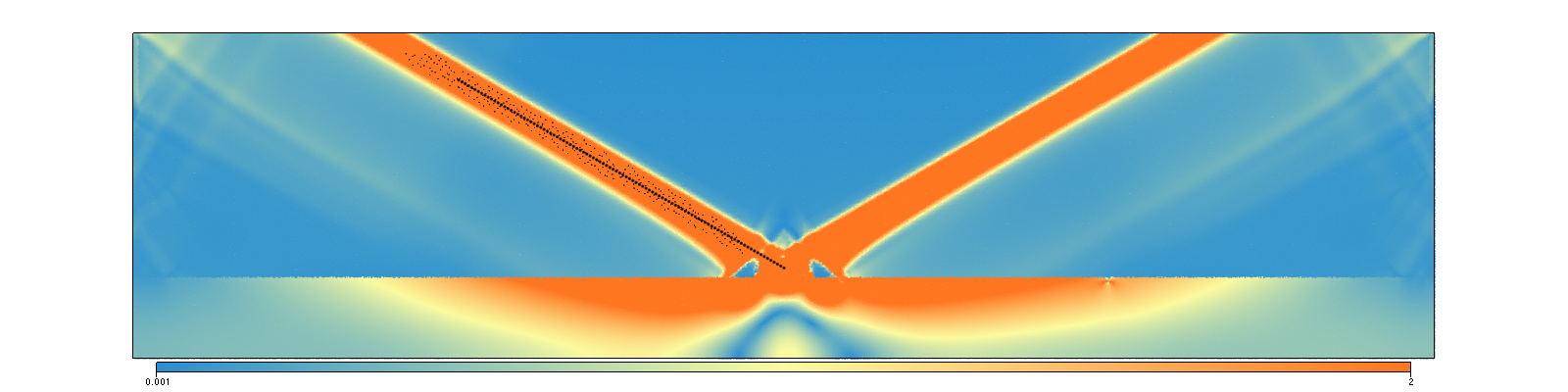
Plasticity & Shear bands
- underworld2 - Mohr Coulomb (trans. isotropic)
\tau_{II} \leq A + B (P_{lith} + \alpha(P')) \leq Y
τII≤A+B(Plith+α(P′))≤Y
- Questions:
- what is the convergence behaviour transversely isotropic model?
deck
By Dan Sandiford
deck
- 686



