Matematik
Trigonometri og eksponentiel udvikling
Opgave 1
Jeg har to funktioner som jeg kender x og y på. Først isolerer jeg b i den første funktion. Herefter isolerer jeg a i den anden og får a til 1/3. Herefter sætter jeg a ind og isolerer b, som jeg får til 9. Nu har jeg a og b og kan lave forskriften for f.

Opgave 2
Jeg ved at startværdien er på 120 og slutværdien på 150. Jeg ved også at tilvæksten skal være på 0,9%. Disse oplysninger sætter jeg ind funktionen for eksponentiel udvikling og isolerer x.
Der går altså ca. 24,91 år siden 1984. Da jeg skal finde årstallet lægger jeg tallene sammen.
1984 + 24,91 = 2008,91
Årstallet skal være 2009.

Opgave 3
Jeg sætter de eksponentielle funktioner lig hinanden og finder x. Herefter sætter jeg x ind i en af funktionerne og finder y.
Skæringspunktet er ca. (1,4, 3,28)

Opgave 4
a) Først finder jeg arealet af grundfladen. Grundfladen er en ligesidet trekant og derfor er alle vinklerne 60 grader. Jeg kan ved hjælp af appelsin-formlen finde arealet af den vilkårlige trekant. Herefter sætter jeg de rigtige værdier ind og omskriver formlen.
Jeg kan nu gange udtrykket med y for at for udtrykket for volumen af figuren. Herefter isolerer jeg y:
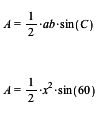
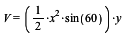
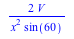
Opgave 4
b) Jeg ved allerede hvordan jeg finder arealet af grundfladen. Man kan sige at figuren har 2 grundflader, så jeg ganger bare udtrykket med 2.
Nu har jeg fundet udtrykket for de to grundflader/trekanter. Jeg mangler bare de 3 firkanter.
Jeg sætter udtrykkene sammen og får:
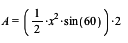
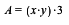
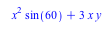
Opgave 4
c) Den første del ( ) af funktionen er udtrykket for arealet af de to trekanter på figuren. Den sidste del af funktionen findes ved at isolere y fra forrige udtryk med rumfanget af figuren. Da jeg kender den konstante volume på 3, så kan jeg isolere y. Jeg får herefter udtrykket for den sidste del af funktionen.
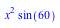


Opgave 4
d)
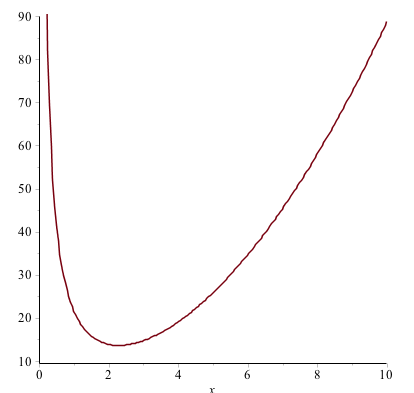
Matematik - Trigonometri og Eksponentielle funktioner
By deam
Matematik - Trigonometri og Eksponentielle funktioner
- 642



