Molekulare Algorithmen
Markus Steinberg & Felix Heinemann
Chemische Digitalcomputermodelle
Aufgabenstellung
-
Chemisches Modell eines 3-Bit-Subtrahierers
-
Operanden als 3-Bit-Binärzahlen
-
Nichtnegative Subtraktion:
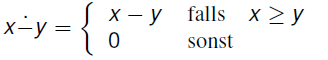
- Experiment: Parameter
Arbeitsablauf
-
Erstellen der Schalttabelle
-
Ermitteln/Vereinfachen der Schaltfunktionen
-
Erstellen der Schaltungen
-
Erstellen der chemischen Modelle
-
Testen der chemischen Modelle
-
Testen der Reaktionsparameter
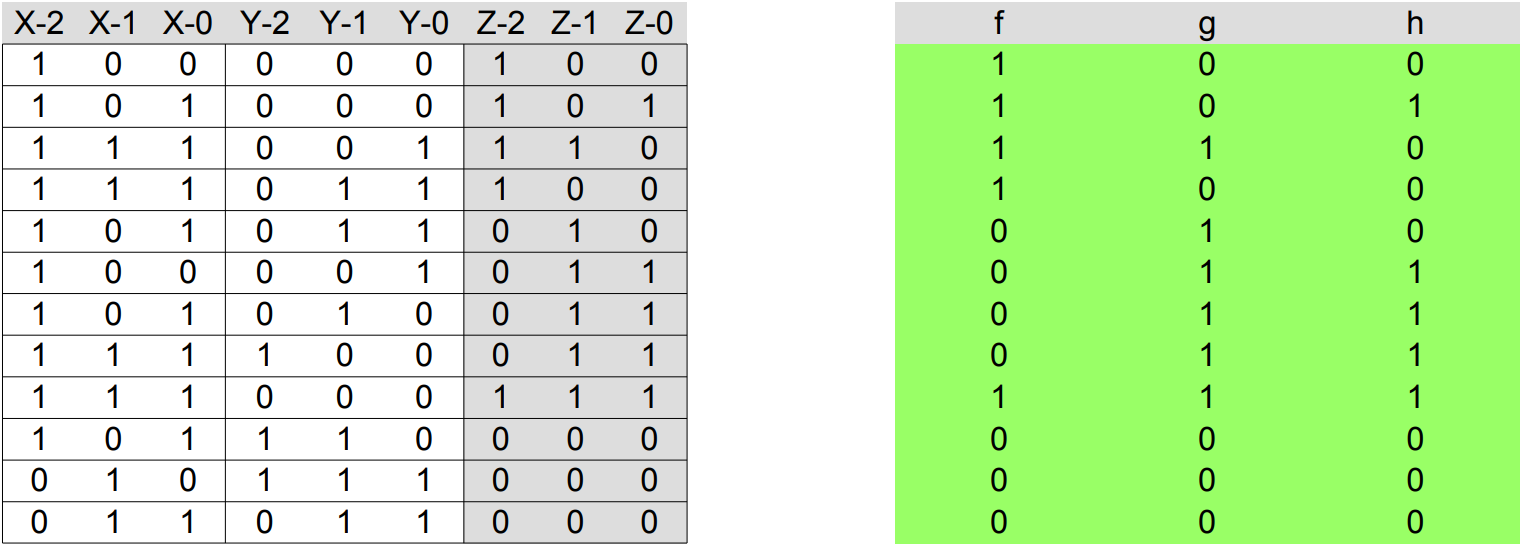
Schalttabelle
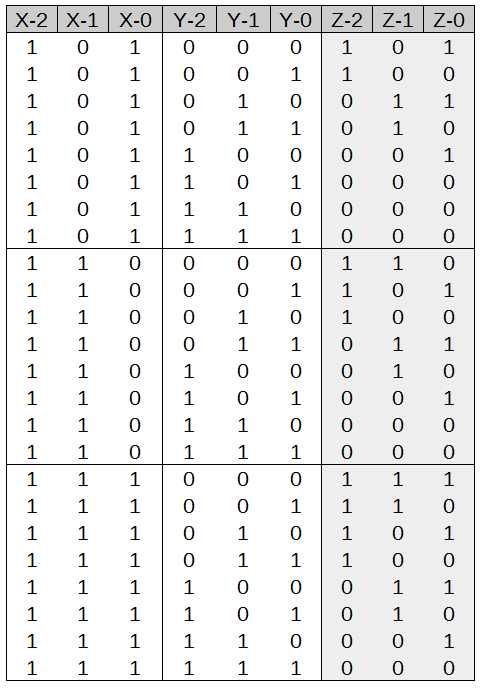
Vereinfachung
-
Algorithmus: Quine-McCluskey
-
Idee:
-
Eine Funktion je Ausgabebit
-
DNF aus Mintermen der Schalttabelle
-
Verschmelzen von Konjunktionstermen
-
-
Bedingung:
(x _ 0 \land x_1 \land x_2) \lor (x_0 \land x_1 \land \overline x_2) = (x_0 \land x_1)
Schaltfunktionen
f = z_2 =
(x_2\land \overline y_2\land \overline y_1\land \overline y_0) \lor
(x_2\land x_0\land \overline y_2\land \overline y_1)
\lor (x_2\land x_1\land \overline y_2\land \overline y_0) \lor
(x_2\land x_1\land \overline y_2\land \overline y_1)
\lor (x_2\land x_1\land x_0\land \overline y_2)
Schaltfunktionen
g = z_1 =
(x_1\land \overline y_2\land \overline y_1\land \overline y_0) \lor
(x_1\land x_0\land \overline y_2\land \overline y_1) \lor
(x_2\land x_1\land \overline y_1\land \overline y_0) \lor
(x_2\land x_1\land x_0\land \overline y_1) \lor
(x_2\land \overline x_1\land \overline y_2\land y_1 \land \overline y_0) \lor
(x_2\land \overline x_1\land x_0\land \overline y_2 \land y_1) \lor
(x_2\land \overline x_1\land \overline x_0\land \overline y_2\land \overline y_1 \land y_0) \lor
(x_2\land x_1\land \overline x_0\land \overline y_2 \land y_1 \land y_0)
h = z_0 =
(x_0\land \overline y_2\land \overline y_1\land \overline y_0) \lor
(x_1\land x_0\land \overline y_2\land \overline y_1) \lor
(x_2\land \overline x_0\land \overline y_2\land y_0) \lor
(x_2\land x_0\land \overline y_1\land \overline y_0) \lor
(x_2\land x_0\land \overline y_2\land \overline y_0) \lor
(x_2\land x_1\land x_0\land \overline y_0) \lor
(x_2\land x_1\land \overline x_0\land \overline y_1\land y_0) \lor
(\overline x_2\land x_1\land \overline x_0\land \overline y_2 \land \overline y_1 \land y_0)
Schaltungen
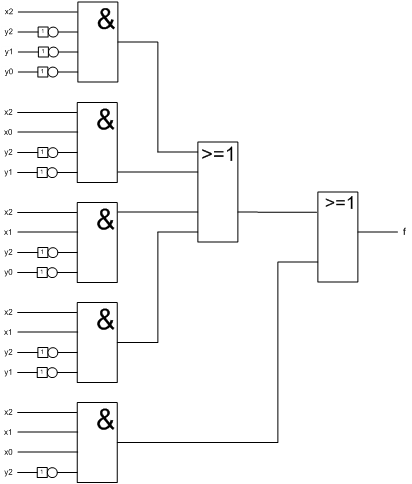
Funktion f = z2
Chemische Modelle
Benötigte Gatter:
- 2 Bit AND
- 4 Bit AND
- 2 Bit OR
- 4 Bit OR
Chemische Modelle
Idee: für jedes Gatter ein Modul
Lösung: JigCell Model Connector
Chemische Modelle
Wiederholung aus der Vorlesung
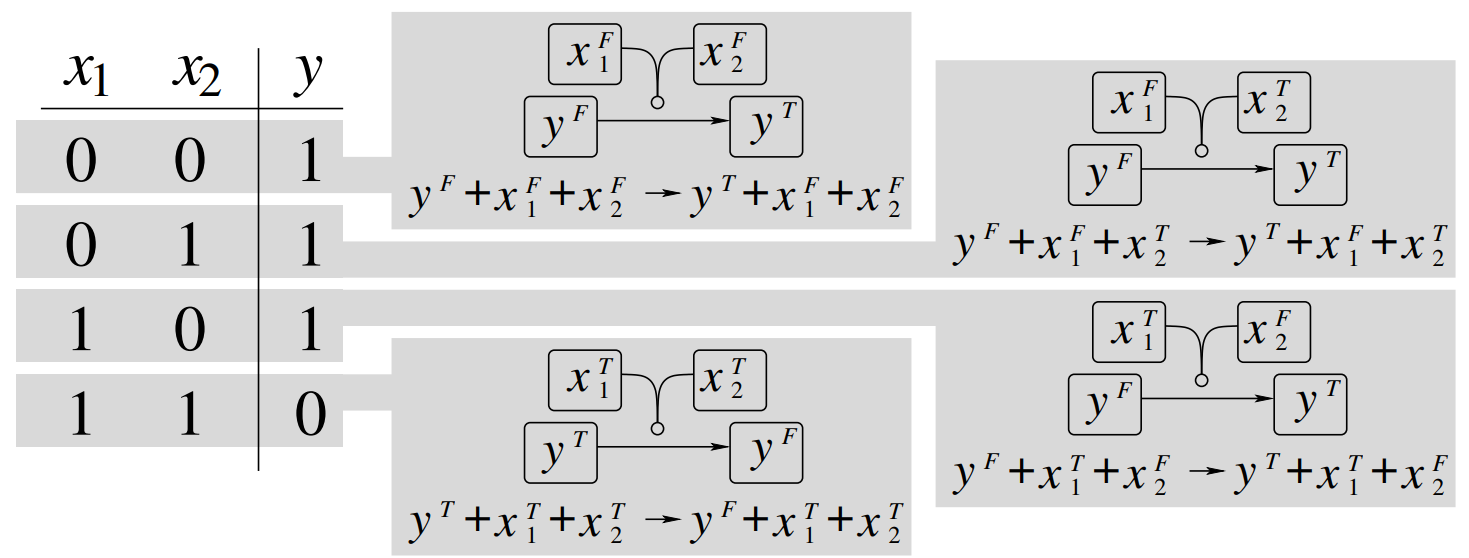
Chemische Modelle
4 Bit AND (COPASI)
Chemische Modelle
Funktion f = z2
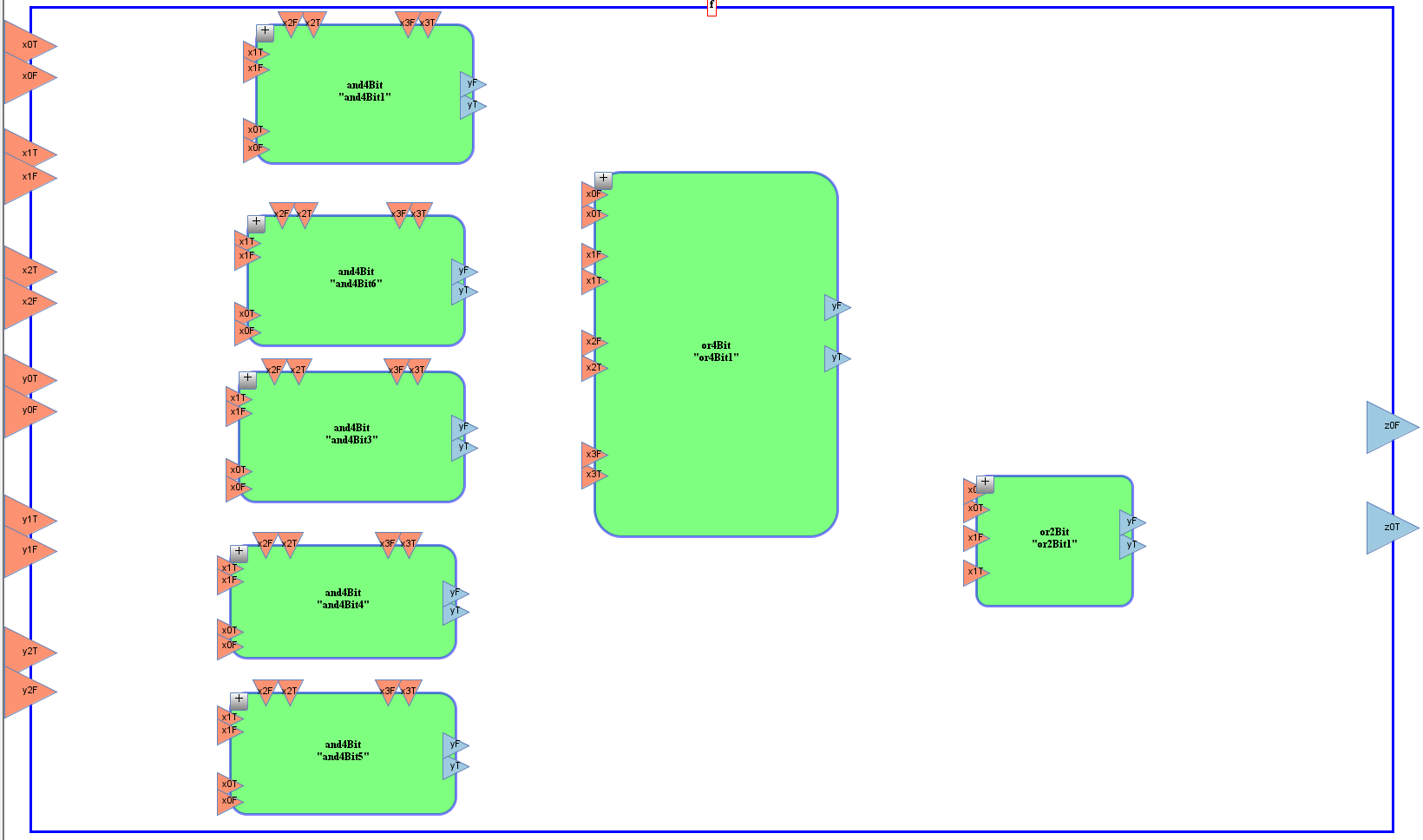
Chemische Modelle
Funktion f = z2
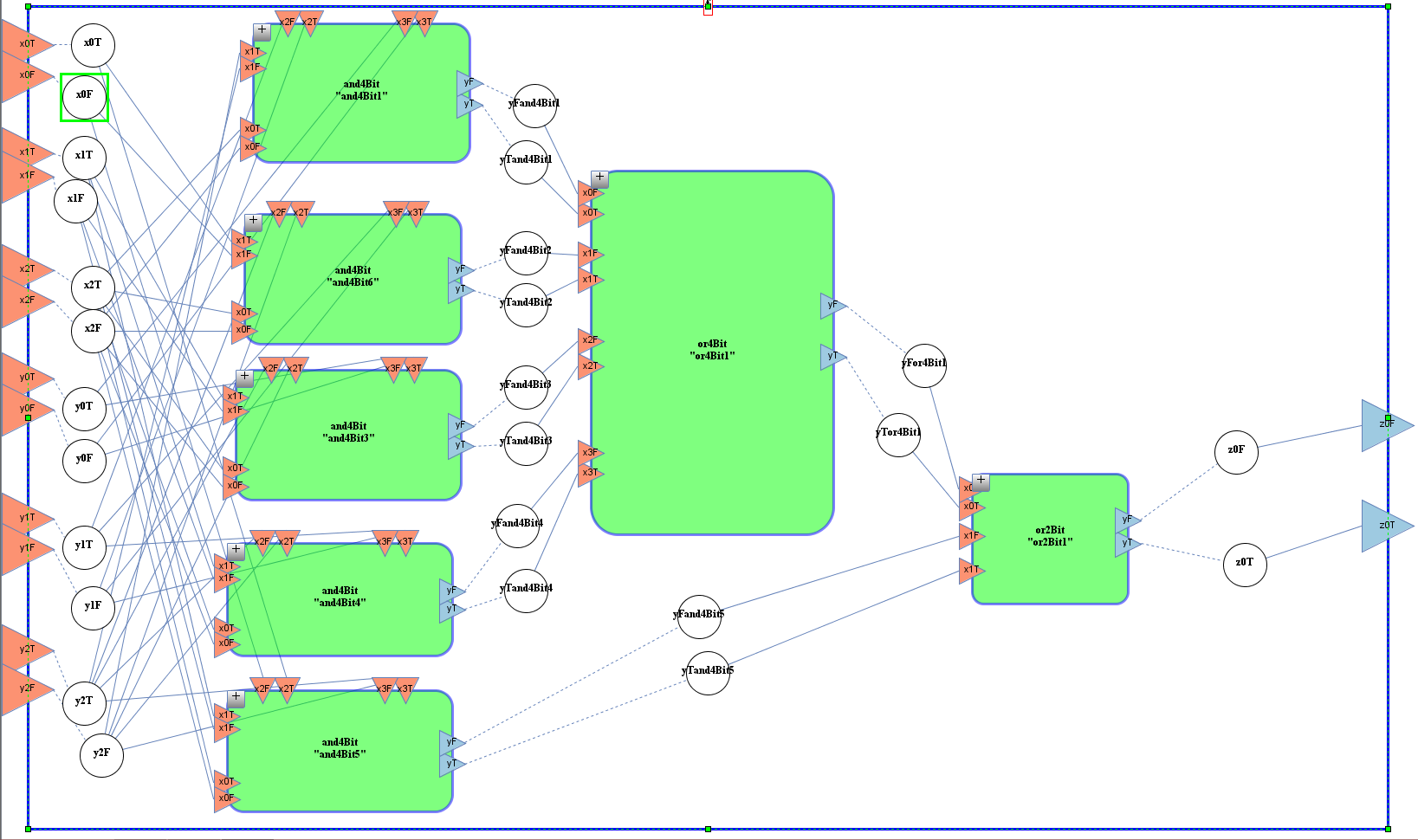
Modell -> Simulation
- JCMC = "Bausteine" zusammensetzen
- Export als SBML (Systems Biology Markup Language)
- Import in COPASI
- Festlegung der Startkonzentrationen
- Simulation
Simulation
111 - 011 = 100
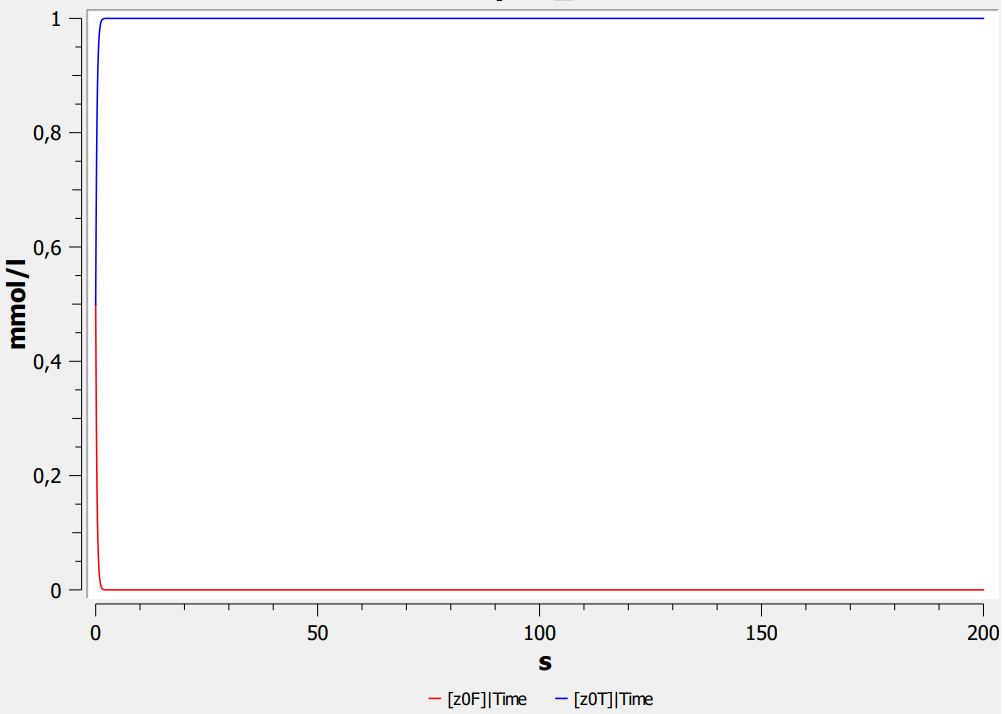
Simulation
111 - 011 = 100
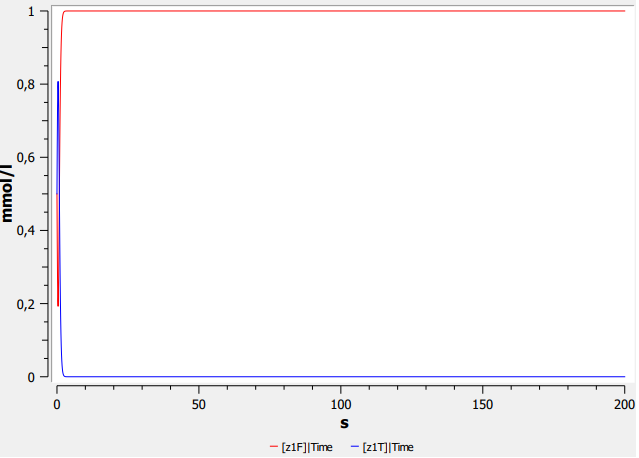
Simulation
111 - 011 = 100
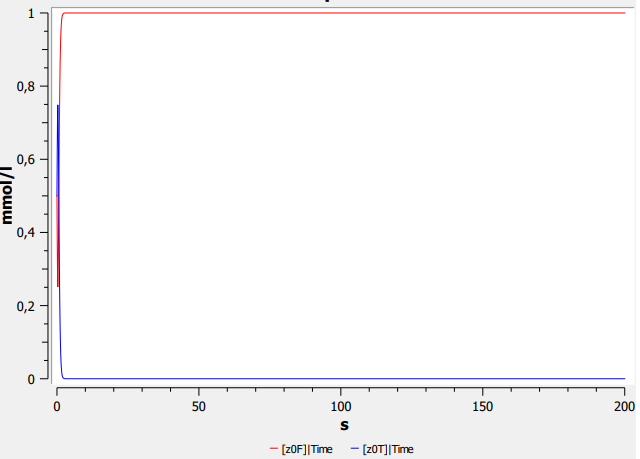
Simulation
Reaktionskonstante
- Höhere Konstante = Schnellere Reaktion
- Schnellere Reaktion = Schneller bei 99% des Zielwerts
- Experimentell diese Abhängigkeit darstellen
Reaktionskonstante
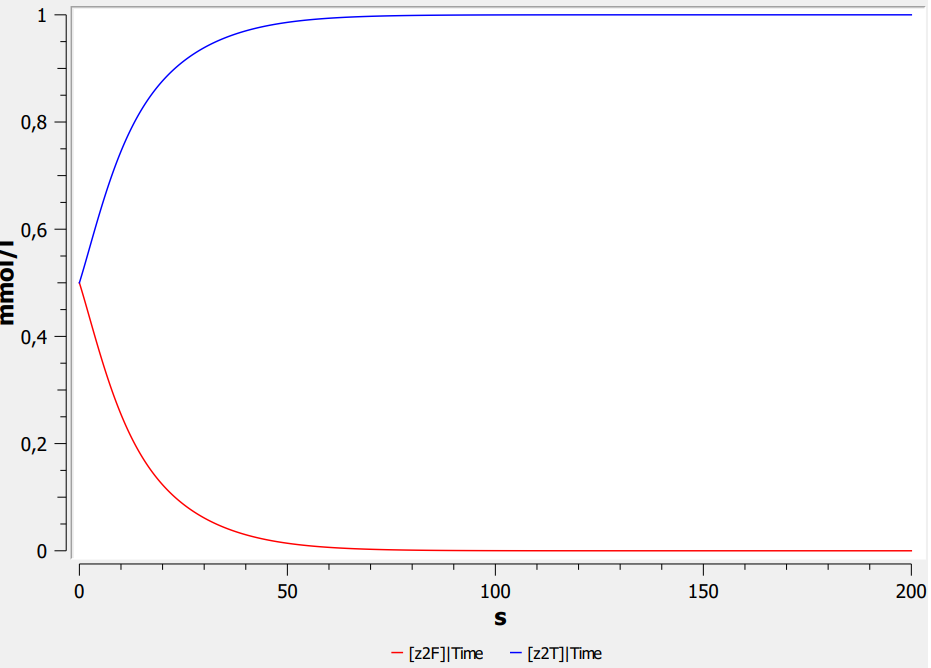
k = 0.1
Reaktionskonstante
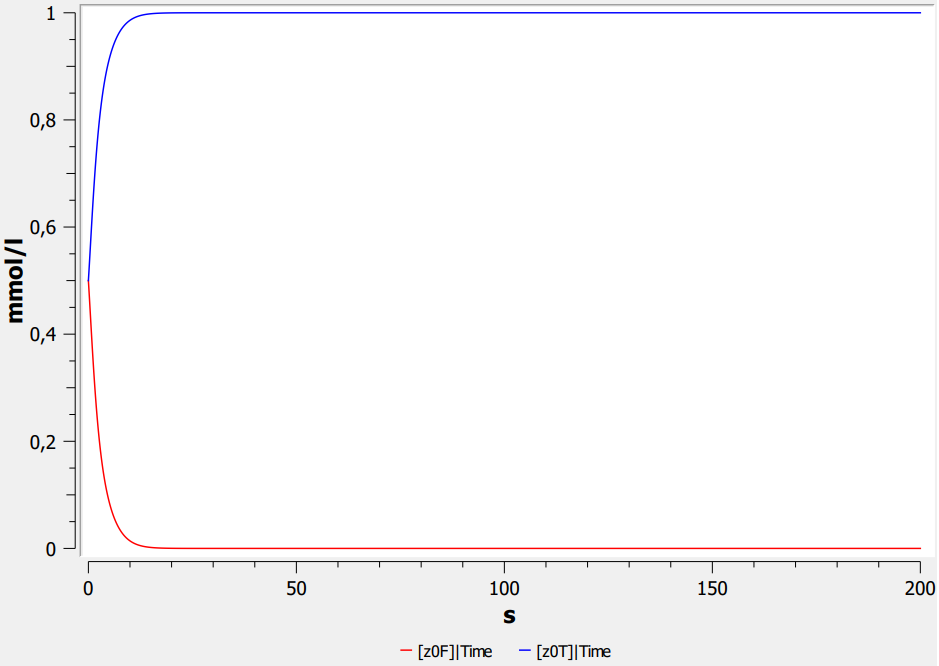
k = 0.5
Reaktionskonstante
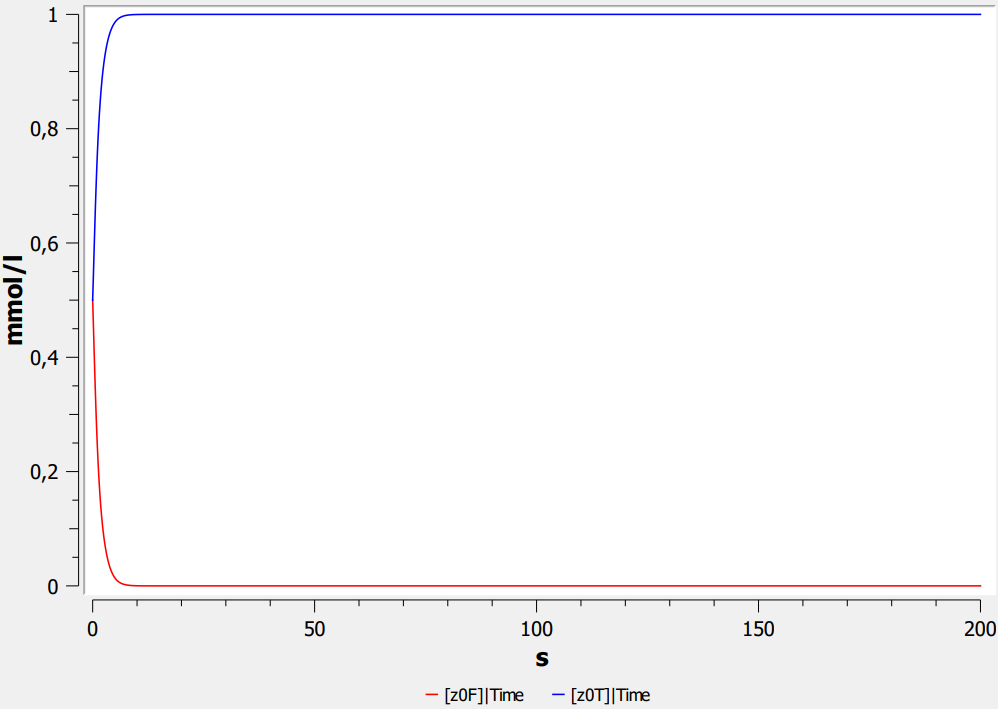
k = 1.0
Reaktionskonstante
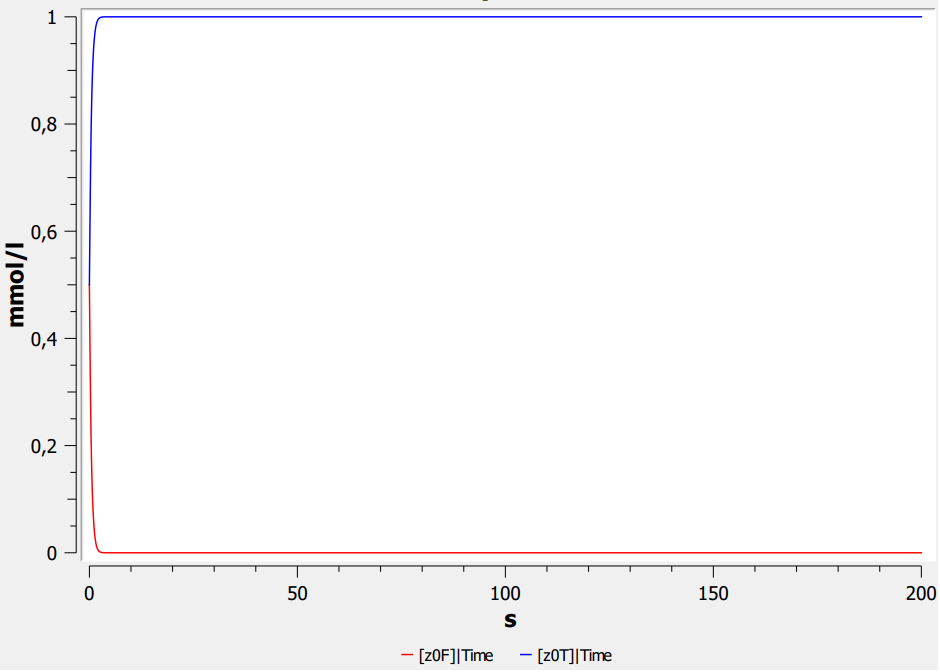
k = 3.0
Reaktionskonstante
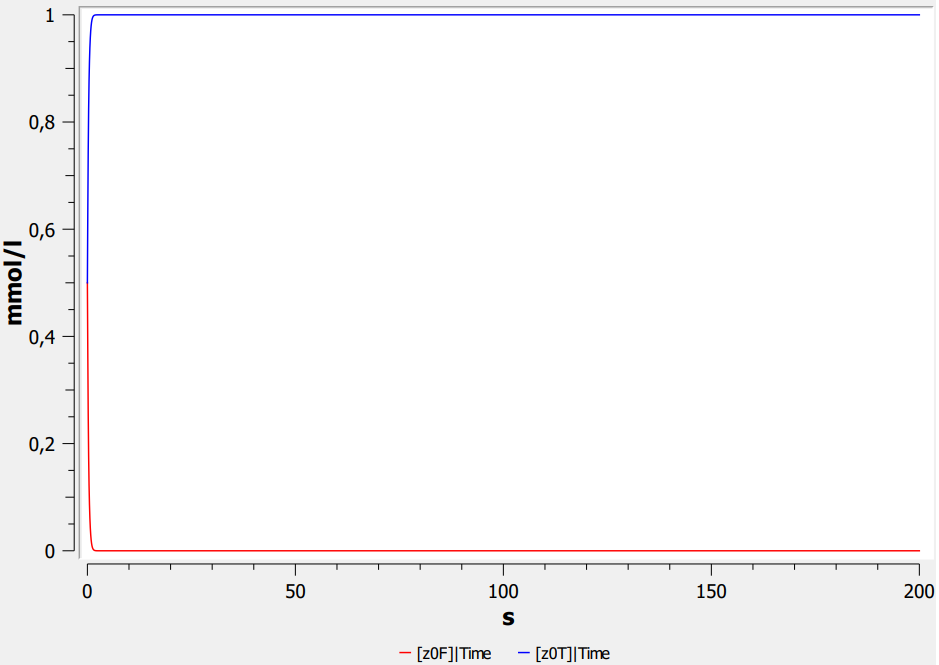
k = 5.0
Reaktionskonstante
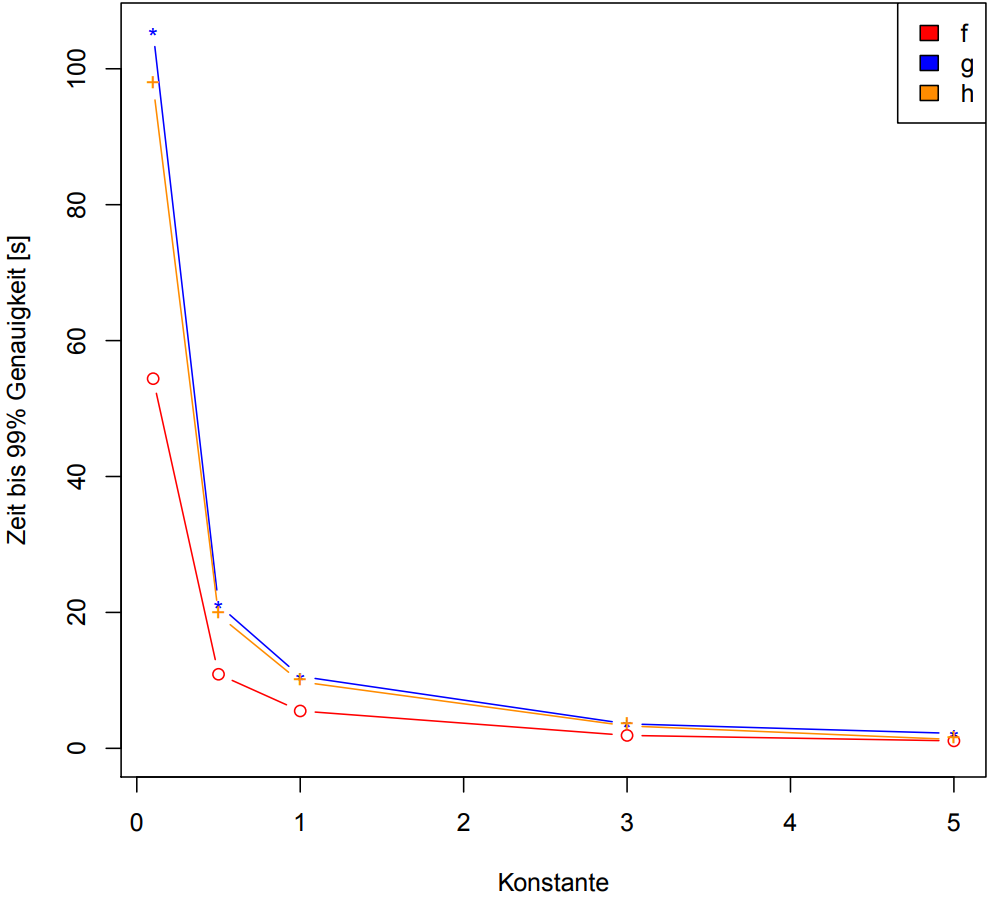
Fragen?
Molekulare Algorithmen
By diangryus
