Accounting for Repetition

https://slides.com/djjr/accounting

EN.501.152.01.FA25

Ryan: FYS Computational Reasoning Fall 2025

Repetition

as sequence + contingency

repeat
   stuff
until done
stuff

done?

LO1: Getting a feeling for (orders of) magnitude

1

LO2: Best, Worst, Average Cases

2

LO3: "on the order of"

3

"are we talking inches or miles?" "is 'short time' days or months?"

powers of ten

ignoring details: dominance of highest polynomial term

families of size: "BIG O" notation

4

LO4: Counting a Few Repetitive Solutions

bubble sort

merge

merge sort

powerset

valentines

queens

LO1: Getting a feeling for (orders of) magnitude

CT 2025

Old Dad Tricks
1. Write out the numbers from one to one million and I'll give you a hundred dollars, kid.

Think It Through
1. How long does it take me to write out numbers 1 to 10? About 10 seconds.
2. How about 1000 to 1010? About 20 seconds.

3. How about 900,000 to 900,001? Also about 20 seconds.
Conclusion: average time per number is between 1 and 2 seconds.

Fast version would be total of 1,000,000 seconds = 16,667 minutes = 277 hours = 12 days.

About 36 cents per hour.

CT 2025

Old Dad Tricks
1. Fold this paper in half 40 times and then stand on top of it. Where are you?

Think It Through
1. Thickness of one sheet is about 0.1mm.
2. First five folds: Fold→0.2mm. Fold→0.4mm. Fold→0.8mm. Fold→1.6mm. Fold→3.2mm.

3. Folds 6-10: Fold→6.4mm. Fold→12.8mm. Fold→25.6mm. Fold→51.2mm. Fold→10.2cm.

4. Folds 11-15: Fold→20.4cm. Fold→40.8cm. Fold→81.6cm. Fold→1.6m. Fold→3.2m.

5. Folds 16-20: Fold→6.4m. Fold→12.8m. Fold→25.6m. Fold→51.2m. Fold→102m.

6. Folds 21-25: Fold→204m. Fold→408m. Fold→816m. Fold→1.6km. Fold→3.2km.

7. Folds 26-30: Fold→6.4km. Fold→12.8km. Fold→25.6km. Fold→51.2km. Fold→102.4km.

8. Folds 31-35: Fold→204km. Fold→408km. Fold→816km. Fold→1632km. Fold→3264km.

9. Folds 36-40: Fold→6,528km. Fold→13,056km. Fold→26,112km. Fold→52,224km. Fold→104,448km. 

Which is about 1/3 of the distance to the moon. Two more folds and we've reached the moon.

LO2: Best, Worst, Average Cases

LO2: Best, Worst, Average Cases

I timed myself writing down numbers. For very small numbers I was able to average under one second per number.  For very high (6 digit) numbers I took almost two seconds per number.

WHAT'S THE BEST WAY TO REPRESENT THIS?

Can we do worst and best case thinking?

I timed myself writing down numbers. For very small numbers I was able to average under one second per number.  For very high (6 digit) numbers I took almost two seconds per number.

Best and worst case. The kids are in line by height. New kid arrives. We start from the front of the line and if new kid is taller that this kid, we move on to the next one.

Best case: the new kid is shorter than the first kid in line so they just get in the front of the line.

Worst case: the new kid is taller than everyone so we have to compare them to each kid in turn until they take their place at the end of the line.

Best and worst case. We use our awkward version of bubble sort.

Best case: cards are already sorted. One round of N compares confirms cards are in order.

Worst case: cards in reverse order. We need to do N rounds of N compares.

swaps=false
home
repeat
    compare
    while compare succeeds
        if L>R
            swap
            swaps = true
until no swaps

N compares every time

5         5

 

5         5

7         7

 

7         7

10       10

 

10       10

K        K

 

K         K

4         4

 

4         4

5         5

 

5         5

7         7

 

7         7

10       10

 

10       10

K        K

 

K         K

4         4

 

4         4

This happens at least once. Then 1 time for each card that has to get moved to the right.

What is your morning routine to get to this class?

Step Description when it goes well? Best Time Estimate Description when $#!+ happens? Worst Time Estimate
Get out of bed
Walk to class

Total

Get Out of Bed

?

?

?

Walk to Class

Total

STOP+THINK

What's the right way to come up with the average case for how long it takes to get to this class?

Get Out of Bed

?

?

?

Walk to Class

"are we talking about inches or miles?" "is 'short time' days or months?"

powers of ten

dominance of highest polynomial term

LO3: "on the order of"

"are we talking about inches or miles?" "is 'short time' days or months?"

powers of ten

dominance of highest polynomial term

LO3: "on the order of"

  1. Suppose you are very good at "20-questions" to try to identify a person in a group. You are so good at the game that every time you ask a question you manage to eliminate half the people still under consideration. In how big a group could you find a person in N questions?
     

  2. The number of different possible topping combinations on a pizza if each of N toppings can be either on or off.
     

  3. We have 10 cookies in a cookie jar for our N guests.
     

  4. The total number of valentines sent in a class of size N if if everyone sends one to everyone else.
     

  5. The number of ways N students could line up for lunch if everyone’s position matters (just do 1,2,3,4,5).
     

  6. The number of idea on the board if each of N people each contributes 1 idea.
     

  7. The total number of sugar cubes in an NxNxN cube (just do 1,2,3,4,5).

EXTRA

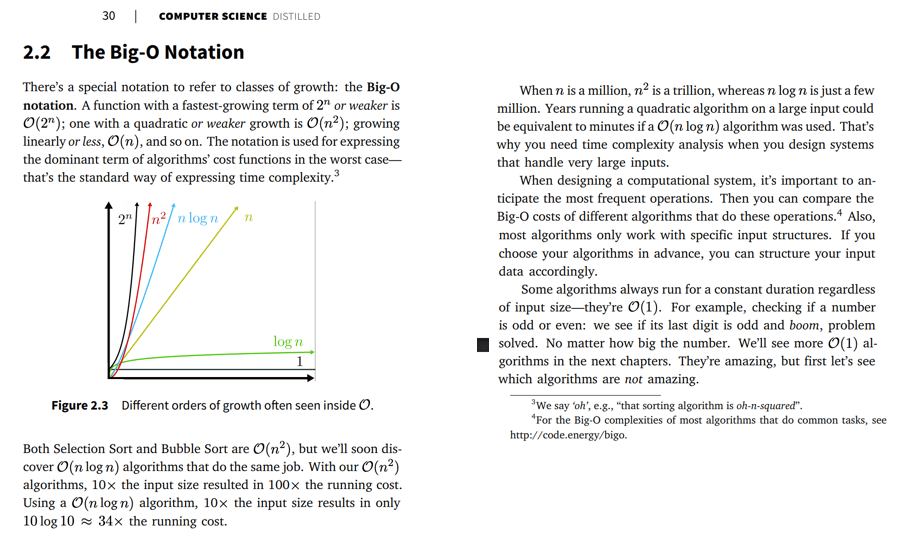
Problems that are "bigger" than polynomial time are sort of unsolveable.

Problems we can solve efficiently

Problems we can check a solution efficiently, but maybe not solve efficiently

So we define a theoretical class of all problems that we can solve in polynomial time and we call it P.

There are harder problems where we can't solve them in polynomial time, but if we had a solution we could verify it in polynomial time. We call this class NP.

P

NP

Problems that are "bigger" than polynomial time are sort of unsolveable.

Problems we can solve efficiently

Problems we can check a solution efficiently, but maybe not solve efficiently

So we define a theoretical class of all problems that we can solve in polynomial time and we call it P.

There are harder problems where we can't solve them in polynomial time, but if we had a solution we could verify it in polynomial time. We call this class NP.

P

NP

\sube

easy to solve

easy to check

easy to solve

easy to check

P

NP

Problems we can solve efficiently

Problems we can check a solution efficiently, but maybe not solve efficiently

P

NP

P \sube NP

easy to solve

easy to check

It's the big open question!

Every problem that's easy to check is easy to solve, we just haven't figured out how.

There are checkable problems that are fundamentally hard to solve.

easy to solve

easy to check

P

NP

BUT ARE THEY EQUAL?

LO3: Counting Loops

bubble sort

merge

merge sort

powerset

valentines

queens

LO4: Counting a Few Repetitive Solutions

LET'S REVISIT Best and worst case. We use our awkward version of bubble sort.

Best case: cards are already sorted. One round of N compares confirms cards are in order.

Worst case: cards in reverse order. We need to do N rounds of N compares.

swaps=false
home
repeat
    compare
    while compare succeeds
        if L>R
            swap
            swaps = true
until no swaps

5         5

 

5         5

7         7

 

7         7

10       10

 

10       10

K        K

 

K         K

4         4

 

4         4

5         5

 

5         5

7         7

 

7         7

10       10

 

10       10

K        K

 

K         K

4         4

 

4         4

Worst case: all of them, N
Best case: none, they are in order.

This happens at least once. Then 1 time for each card that has to get moved to the right.

N compares every time

Counting Our Merge Sort

for h in hands
   if cards(h)>1
      split
   swap=false
repeat
   for h in hands
      merge pairwise
until hands has just 1 element
\sum{splits} = 1 + 2 + 4 + \dots +2^{log_2 N - 1} = \sum_{n=0}^{N}{2^n}= 2^{log_2{N}}-1=N-1
\text{splits} = 1 + 2 + 4 + \dots +2^{log_2 N - 1}

What if we add arranging queens on a chessboard?

Q(5)=5x4x3x2=120

Q(4)=4x3x2=24

F(20)=102m

F(21)=204m

NEXT

BINARY,
LOGIC, and
CIRCUITS

Accounting for Repetition

By Dan Ryan

Accounting for Repetition

CT2025 Introduction to computational complexity

  • 1

More from Dan Ryan