Differential Privacy

Color Mixing

Differential Privacy is kind of like color mixing on hard mode!

Standard data encryption offers little to no protection. Like the color purple, you can easily decipher its constituents (sensitive information) to be red and blue.

Problems with other standard

approaches of data privacy protection

Data Encryption

advanced computer algorithms can decrypt easily

Anonymize

example: a data set includes gender, residence, age, DOB, malaria(?)

---> deduce who the data belongs to

---> sensitive data is leaked

^^ linkage attack

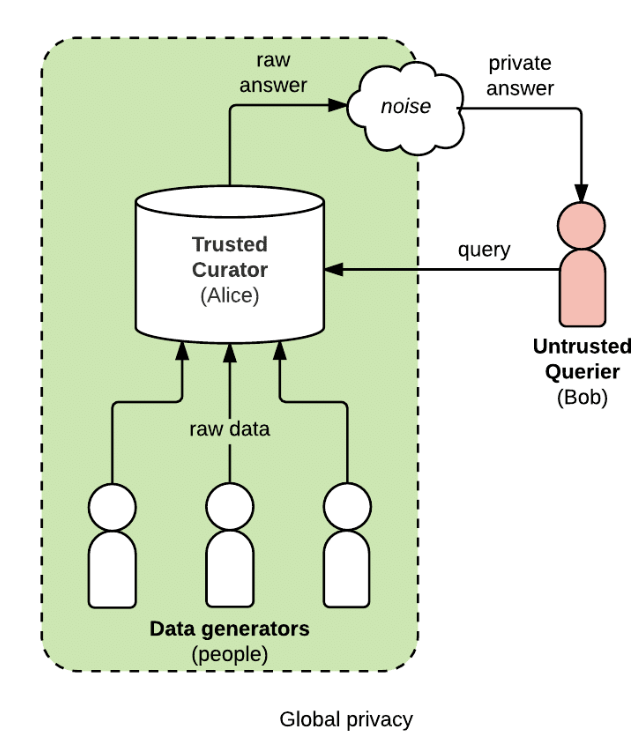
Mediated Access

analysts can ask specific questions to the trusted "curator" to identify who the data belongs to 

We (the data seekers) can still obtain the information that it's green, but much harder to find its exact components

This is differential privacy:

Imagine your raw data is green, but differential privacy encodes it to an ambiguous green like this.

Definition

• Learn nothing about an individual but still learning useful information about a population
  • trade off between privacy and accuracy

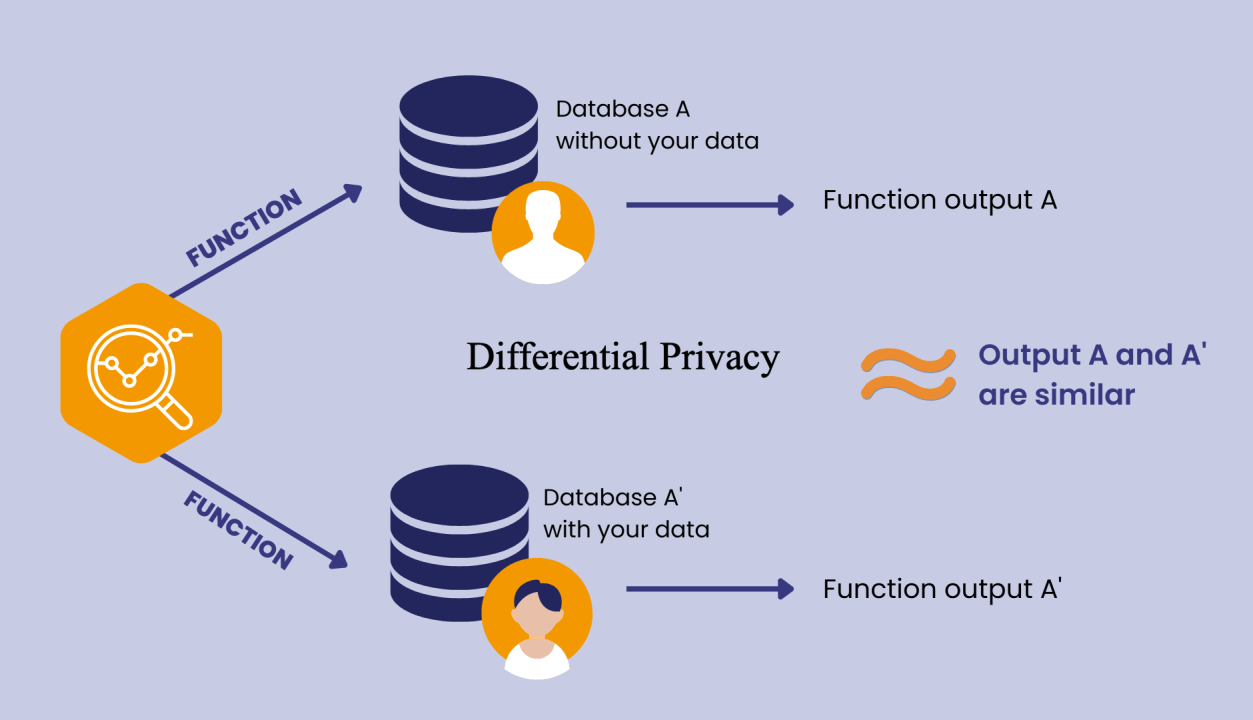
• A concept rather than a specific algorithm
• no additional harm is done to the individual should they provide their data

To achieve differential privacy, we have to introduce randomness. The amount of randomness depends on:

1. sensitivity of the query (global sensitivity) 

2. desired level of privacy

(privacy-utility trade-off)

=  randomness

(aka noise)

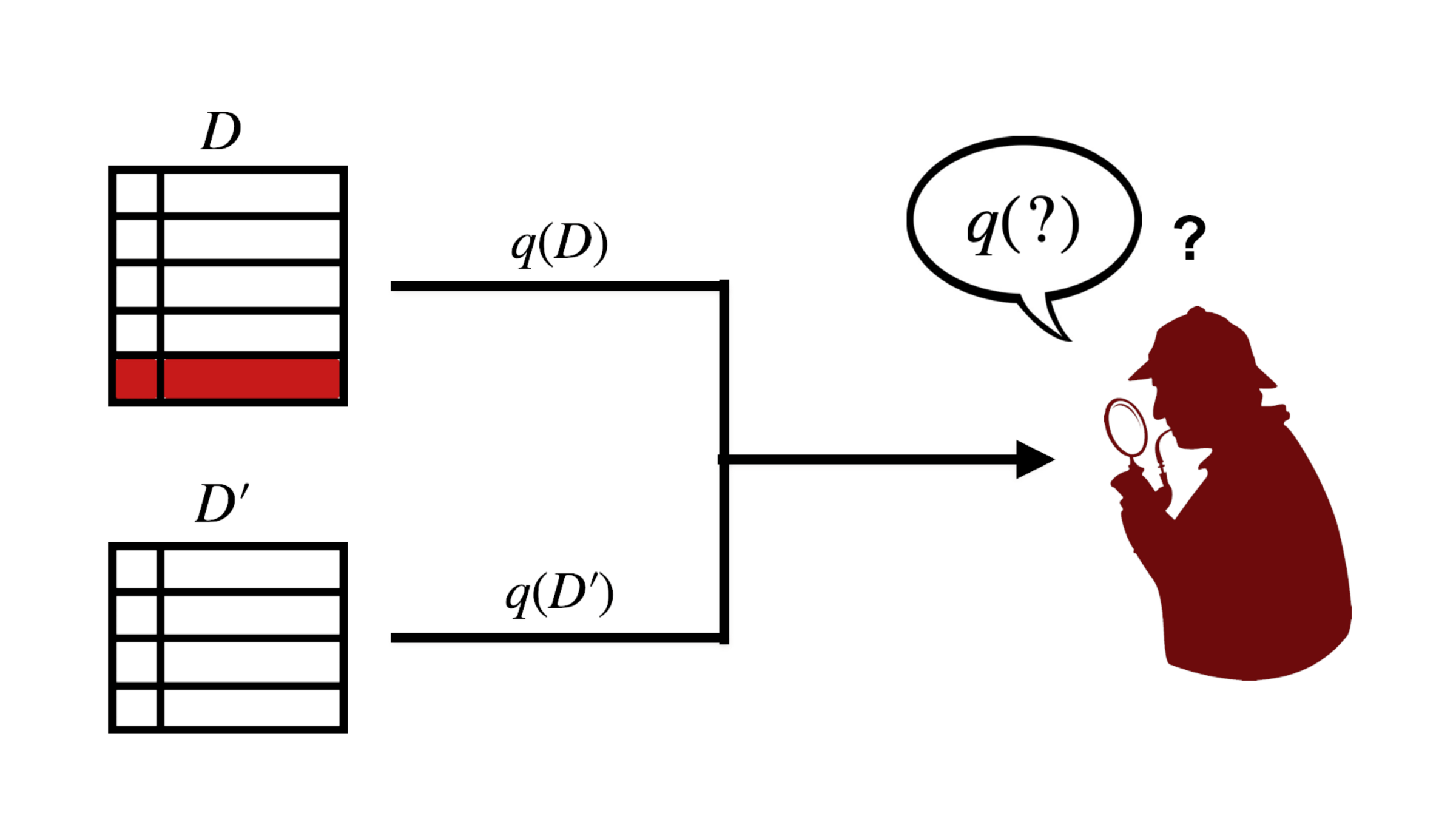
Global Sensitivity

• how much one data entry influences the outcome of a query
• formally: maximum possible difference between the function output on two neighboring data sets

Global Sensitivity

low sensitivity

Query: is it still a mix of colors?

yes

yes

Global Sensitivity

high sensitivity

Query: a mix of how many colors?

3

2

Global Sensitivity

difference of one data entry heavily impacts function output = high sensitivity

• higher sensitivity requires more noise to compensate
• lower sensitivity requires less noise to compensate

difference of one data entry negligibly impacts function output = low sensitivity

Privacy-Utility Trade-off

If you want accuracy, there is less privacy

Easier to infer blue and yellow from green

If you want privacy, there is less accuracy

harder to infer blue and yellow from green

Privacy-Utility Trade-off

Summary of Randomness

• Sensitivity of query: direct relationship with amount of noise we want to add
• Utility: inverse relationship with amount of noise we want to add

How do we add randomness to our data set?

One example: Randomized Response

• developed to collect sensitive/embarrassing information
• participants report whether or not they have property P
• they also do a coin flip:
  • tails = respond truthfully
  • heads = lie
    • second flip:
      • heads = "yes"
      • tails = "no"
  • respondent is not incriminated: at least 1/4 probability that the respondent did not answer honestly

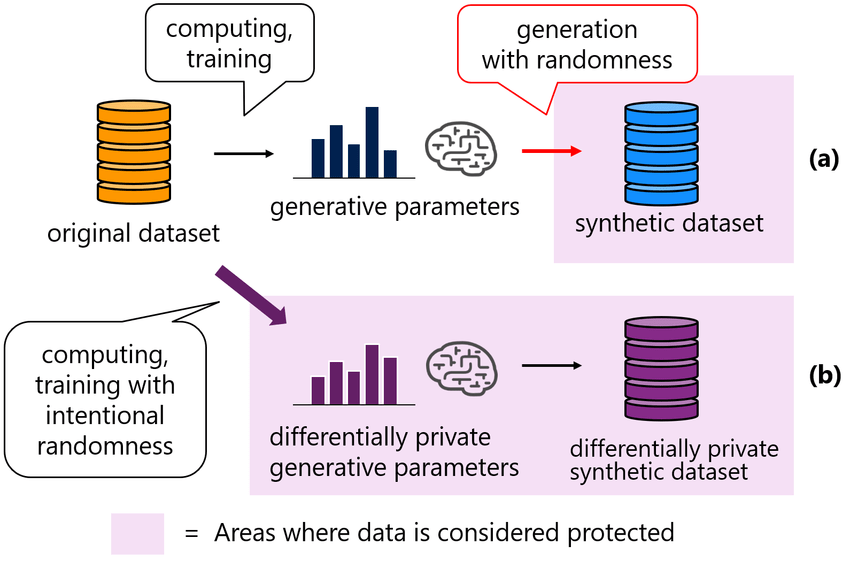
Synthetic Data Set

• A completely new and false set of data that reflects the same attributes as the original data set 
• Example: Given my (only) attribute is number of colors mixed, original data set and synthetic data set have the same attribute(s)!

original

synthetic

Specific Algorithms for Randomization

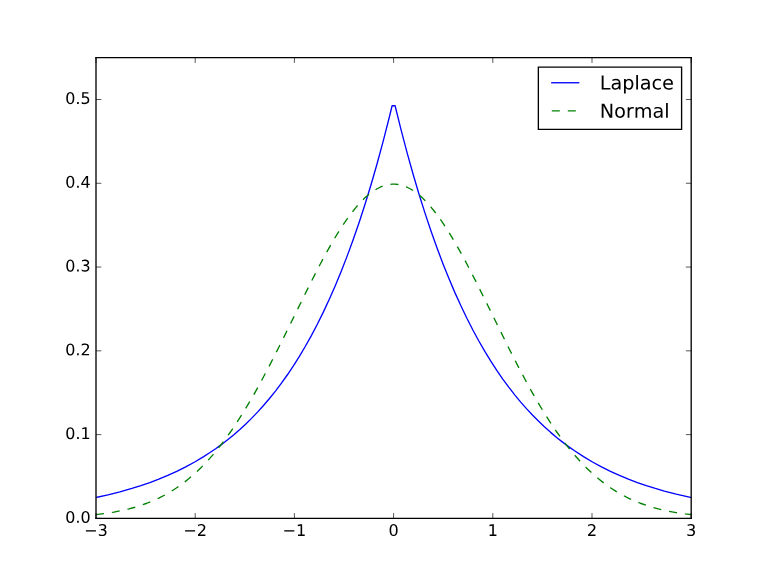
Laplace

• adds noise from laplace distribution
• uses Manhattan distance to determine noise scale
• good for simple numeric queries

Gaussian

• adds noise from normal distribution
• uses Euclidian distance to determine noise scale
• good for complex analysis, multiple queries

Some Implications of Differential Privacy

• quantification of privacy loss 
• protection against arbitrary risks (threshold quantified by researcher)
• protection against post processing (a data analyst cannot deduce the output of algorithm and increase privacy loss)