Optimization of Tree Ensembles

Real World Problem

But also want to know the strategy to make some differences (a.k.a. modify the sample)

When applying a classifier,

sometimes we not only just want to know whether a sample belongs to a class

Examples

  • Medical attention
  • Company decision

First step

Problem Definition

Given us a classifier $$C(\cdot)$$, and an n-features vector $$X = \{x_1, x_2, ..., x_n\}$$

The object is to find another $$X'$$ so that $$ X' = \arg \max_{X'} C(X') $$

How?

Focus on single model

Random Forest

Random Forest

RF is $$ C(X) = \sum_{t=1}^{T} \lambda_t f_t (\textbf{X})$$ here $$ f_i(\cdot) $$ is a tree in the forest.

Example from Iris dataset

How to formulate the problem?

idea: consider it to be a MIP problem

Terminology

Let $$leaves(t)$$ be the set of leaves or terminal nodes of tree t.

Let $$ splits(t) $$ denote the set of splits of tree t (non-terminal nodes).

Let $$ left(s) $$ be the set of leaves that are accessible from the left branch, and same as the $$ right(s) $$

let $$ V(s) \in \{1, . . . , n\}$$ denote the variable that participates in split s,

and let $$ C(s) $$ denote the set of values of variable i that participate in the split query of s.

Object function

$$ \max_{\textbf{x},\textbf{y}} \sum_{t=1}^{T}\sum_{\ell \in \textbf{leaves}(t)} \lambda_t \cdot p_{t,\ell} \cdot y_{t, \ell} $$

Constraints

  • the observation falls in exactly one of the leaves of each tree t
  • if 1 observation falls into the a sub-tree, then no observation could fall into the other part of sub-tree
  • the indicator y must be in {0, 1}

Intermediate variable

$$ x_{i,j} $$ indicates that if a feature $$X_i$$ fulfills the predicate of that node, i.e. $$X_i$$ falls into left branch of the tree

the observation falls in exactly one of the leaves of each tree t

\sum_{\ell \in \textbf{leaves}(t)}y_{t,\ell} = 1, \forall t \in \{1, ..., T\}
∑ℓ∈leaves(t)yt,ℓ=1,∀t∈{1,...,T}\sum_{\ell \in \textbf{leaves}(t)}y_{t,\ell} = 1, \forall t \in \{1, ..., T\}

if 1 observation falls into the a sub-tree, then no observation could fall into the other part of sub-tree

\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈left(s)yt,ℓ≤∑j∈C(s)xV(s),j, ∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈right(s)yt,ℓ≤1−∑j∈C(s)xV(s),j,∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)

Some additional constraints on x

\sum_{j=1}^{K_i} x_{i,j} = 1, \forall i \in \mathcal{C}
∑j=1Kixi,j=1,∀i∈C\sum_{j=1}^{K_i} x_{i,j} = 1, \forall i \in \mathcal{C}
x_{i,j} \leq x_{i, j+1}, \forall i \in \mathcal{N}, j \in \{1, ..., K_i - 1\}
xi,j≤xi,j+1,∀i∈N,j∈{1,...,Ki−1}x_{i,j} \leq x_{i, j+1}, \forall i \in \mathcal{N}, j \in \{1, ..., K_i - 1\}
x_{i,j} \in \{0, 1\}, \forall i \in \{1, ..., n\}, j \in \{1, ..., K_i - 1\},
xi,j∈{0,1},∀i∈{1,...,n},j∈{1,...,Ki−1},x_{i,j} \in \{0, 1\}, \forall i \in \{1, ..., n\}, j \in \{1, ..., K_i - 1\},

the indicator y must be in {0, 1}

y_{t, \ell} \geq 0, \forall t \in \{1,...,T\}, \ell \in \textbf{leaves}(t)
yt,ℓ≥0,∀t∈{1,...,T},ℓ∈leaves(t)y_{t, \ell} \geq 0, \forall t \in \{1,...,T\}, \ell \in \textbf{leaves}(t)

Trick kicks in!

All in one

\max_{\textbf{x},\textbf{y}} \sum_{t=1}^{T}\sum_{\ell \in \textbf{leaves}(t)} \lambda_t \cdot p_{t,\ell} \cdot y_{t, \ell}
maxx,y∑t=1T∑ℓ∈leaves(t)λt⋅pt,ℓ⋅yt,ℓ\max_{\textbf{x},\textbf{y}} \sum_{t=1}^{T}\sum_{\ell \in \textbf{leaves}(t)} \lambda_t \cdot p_{t,\ell} \cdot y_{t, \ell}
subject \ to\ \sum_{\ell \in \textbf{leaves}(t)}y_{t,\ell} = 1, \forall t \in \{1, ..., T\}
subject to ∑ℓ∈leaves(t)yt,ℓ=1,∀t∈{1,...,T}subject \ to\ \sum_{\ell \in \textbf{leaves}(t)}y_{t,\ell} = 1, \forall t \in \{1, ..., T\}
\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈left(s)yt,ℓ≤∑j∈C(s)xV(s),j, ∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈right(s)yt,ℓ≤1−∑j∈C(s)xV(s),j,∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
\sum_{j=1}^{K_i} x_{i,j} = 1, \forall i \in \mathcal{C}
∑j=1Kixi,j=1,∀i∈C\sum_{j=1}^{K_i} x_{i,j} = 1, \forall i \in \mathcal{C}
x_{i,j} \leq x_{i, j+1}, \forall i \in \mathcal{N}, j \in \{1, ..., K_i - 1\}
xi,j≤xi,j+1,∀i∈N,j∈{1,...,Ki−1}x_{i,j} \leq x_{i, j+1}, \forall i \in \mathcal{N}, j \in \{1, ..., K_i - 1\}
x_{i,j} \in \{0, 1\}, \forall i \in \{1, ..., n\}, j \in \{1, ..., K_i - 1\},
xi,j∈{0,1},∀i∈{1,...,n},j∈{1,...,Ki−1},x_{i,j} \in \{0, 1\}, \forall i \in \{1, ..., n\}, j \in \{1, ..., K_i - 1\},
y_{t, \ell} \geq 0, \forall t \in \{1,...,T\}, \ell \in \textbf{leaves}(t)
yt,ℓ≥0,∀t∈{1,...,T},ℓ∈leaves(t)y_{t, \ell} \geq 0, \forall t \in \{1,...,T\}, \ell \in \textbf{leaves}(t)

Approximation

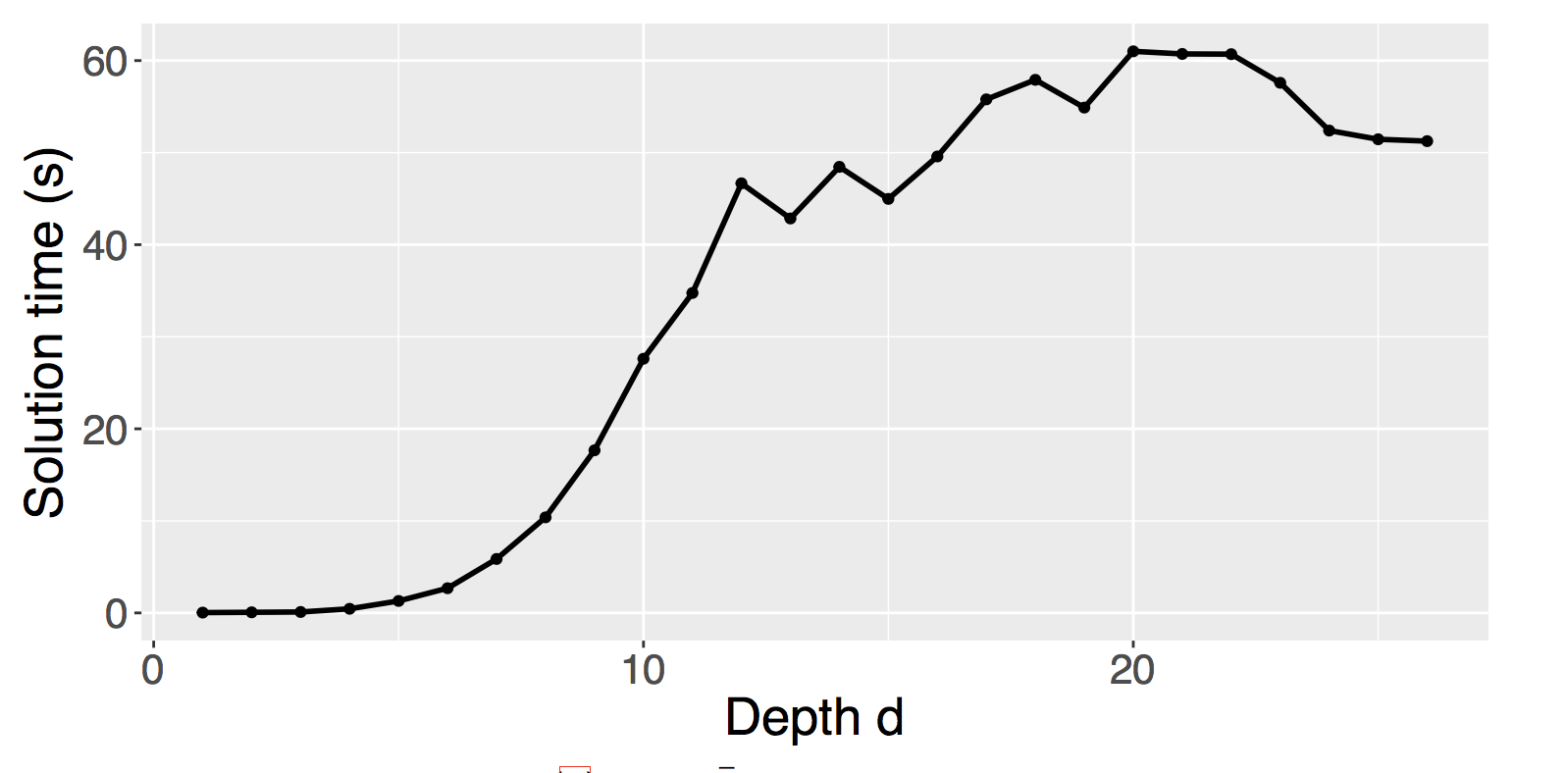
It's quite time-consuming to solve the original problem ​

\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈left(s)yt,ℓ≤∑j∈C(s)xV(s),j, ∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈right(s)yt,ℓ≤1−∑j∈C(s)xV(s),j,∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)

Traverse the whole forest, O(k*2^n)!

Idea: what if we do not search to the deepest of the tree?

$$ \Omega = \{(t,s)|t \in \{1,...,T\}, s \in splits(t) \} $$

First define

\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall (t,s) \in \bar{\Omega}
∑ℓ∈left(s)yt,ℓ≤∑j∈C(s)xV(s),j, ∀(t,s)∈Ω¯\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall (t,s) \in \bar{\Omega}
\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall (t,s) \in \bar{\Omega}
∑ℓ∈right(s)yt,ℓ≤1−∑j∈C(s)xV(s),j,∀(t,s)∈Ω¯\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall (t,s) \in \bar{\Omega}
\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈left(s)yt,ℓ≤∑j∈C(s)xV(s),j, ∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{left}(s)} y_{t, \ell} \leq \sum_{j \in \textbf{C}(s)}x_{\textbf{V}(s), j}, \ \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)
∑ℓ∈right(s)yt,ℓ≤1−∑j∈C(s)xV(s),j,∀t∈{1,...,T},s∈splits(t)\sum_{\ell \in \textbf{right}(s)} y_{t, \ell} \leq 1 - \sum_{j \in \textbf{C}(s)} x_{\textbf{V}(s), j}, \forall t \in \{1, ..., T\}, s \in \textbf{splits}(t)

Proposion

Z^*_{MIO,1} \geq Z^*_{MIO,2} \geq... \geq Z^*_{MIO,d_{max}} \geq Z^*_{MIO}
ZMIO,1∗≥ZMIO,2∗≥...≥ZMIO,dmax∗≥ZMIO∗Z^*_{MIO,1} \geq Z^*_{MIO,2} \geq... \geq Z^*_{MIO,d_{max}} \geq Z^*_{MIO}

Where Z is the objective value

Theorem

\delta_{t,s} = max \{ \max_{\ell \in left(s)} p_{t,\ell} - \min_{\ell \in left(s)} p_{t,\ell}, \max_{\ell \in right(s)} p_{t,\ell} - \min_{\ell \in right(s)} p_{t,\ell} \}
δt,s=max{maxℓ∈left(s)pt,ℓ−minℓ∈left(s)pt,ℓ,maxℓ∈right(s)pt,ℓ−minℓ∈right(s)pt,ℓ}\delta_{t,s} = max \{ \max_{\ell \in left(s)} p_{t,\ell} - \min_{\ell \in left(s)} p_{t,\ell}, \max_{\ell \in right(s)} p_{t,\ell} - \min_{\ell \in right(s)} p_{t,\ell} \}
\Delta_t = \max_{s \in splict(t,d)} \delta_{t,s}
Δt=maxs∈splict(t,d)δt,s\Delta_t = \max_{s \in splict(t,d)} \delta_{t,s}
Z^*_{MIO,d} - \sum^T_{t=1} \lambda_t \Delta_t \leq Z_d \leq Z^*_{MIO} \leq Z^*_{MIO,d}
ZMIO,d∗−∑t=1TλtΔt≤Zd≤ZMIO∗≤ZMIO,d∗Z^*_{MIO,d} - \sum^T_{t=1} \lambda_t \Delta_t \leq Z_d \leq Z^*_{MIO} \leq Z^*_{MIO,d}

Experiments

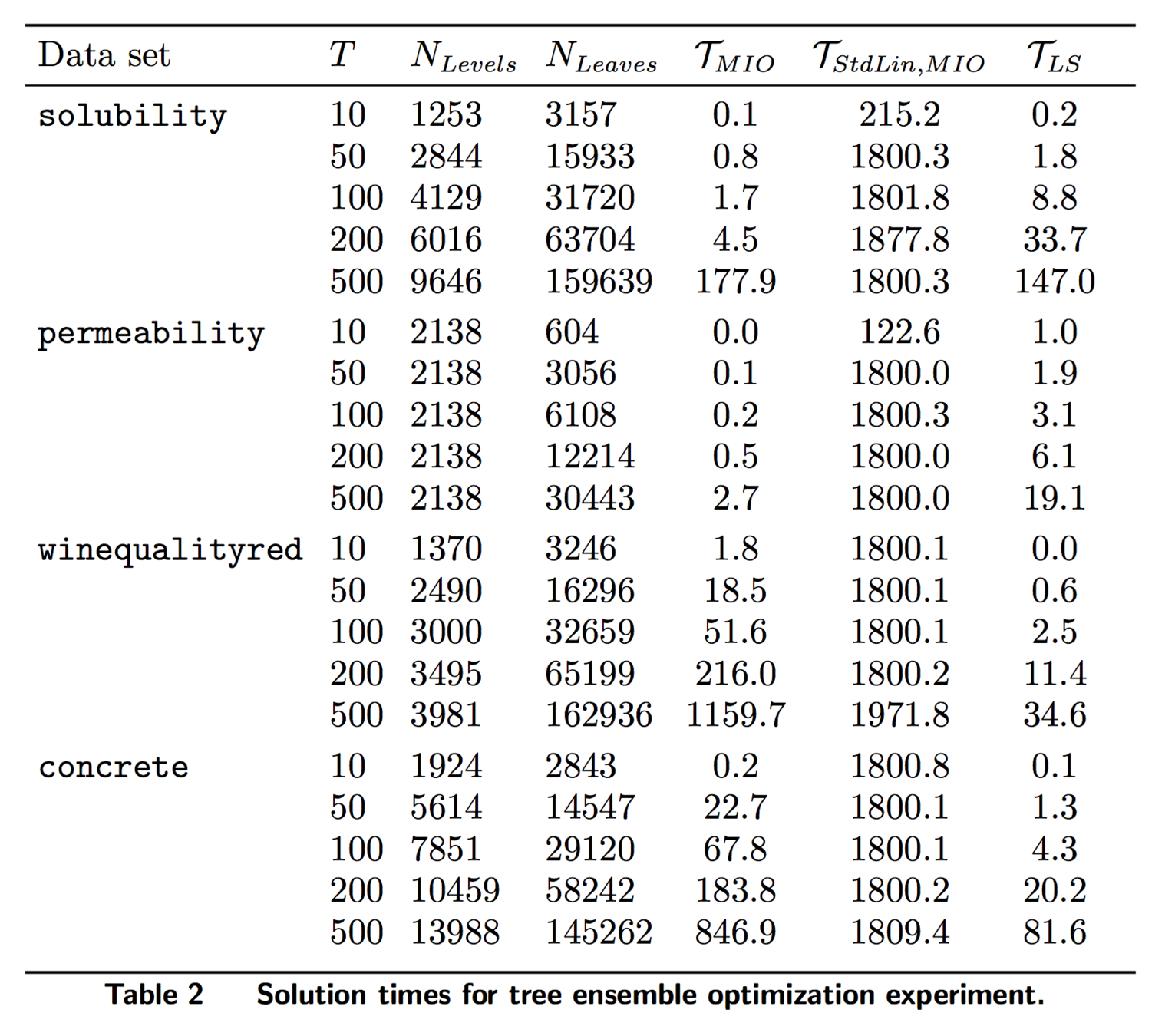
Experiments

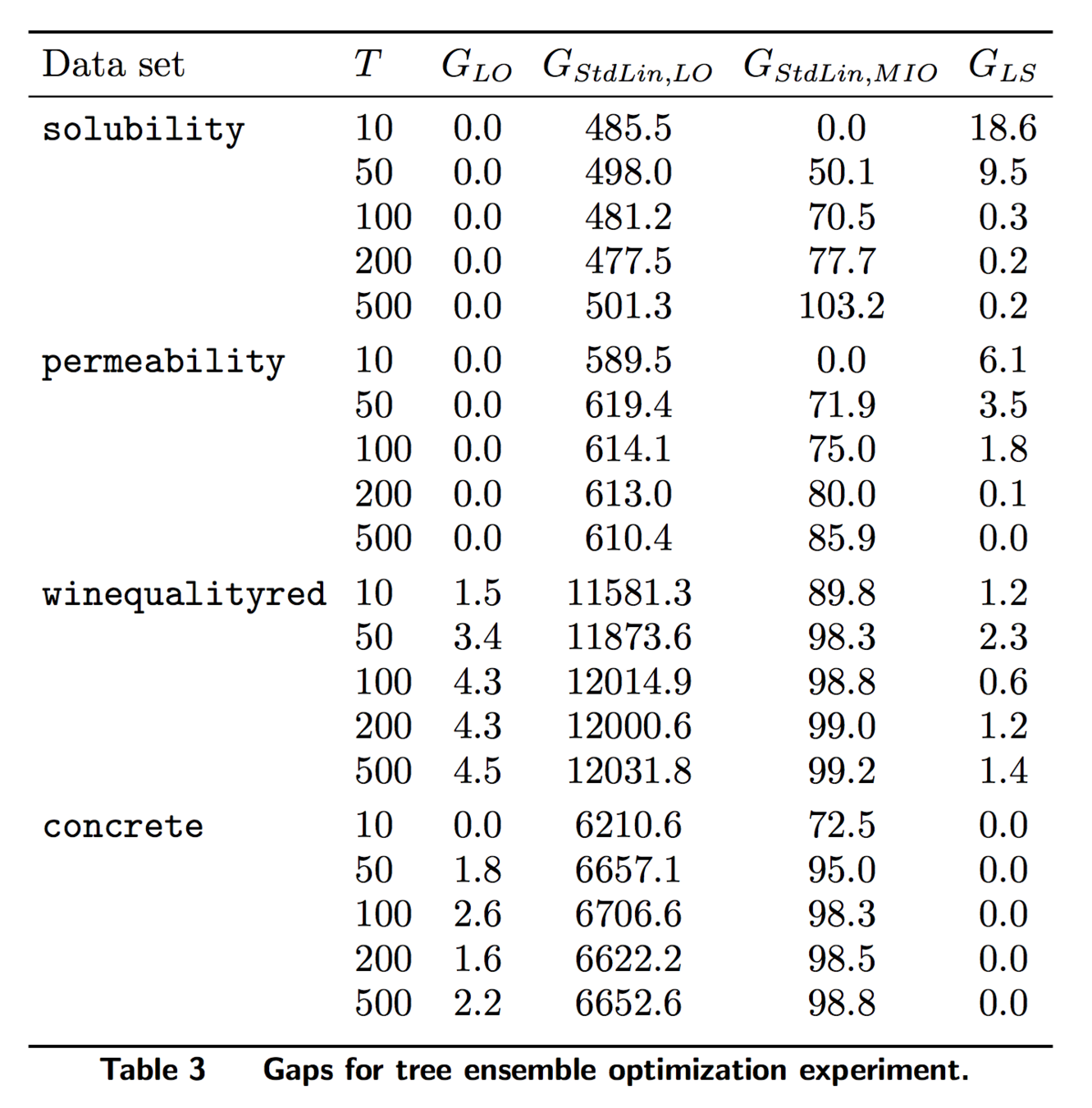
Experiments

Optimization of Tree Ensembles

By Weiyüen Wu

Made with Slides.com

Optimization of Tree Ensembles

  • 599

More from Weiyüen Wu