Electrostatics
The Electric Force
Electrostatics
The Electric Force
Coulomb's Law
Phenomenological approach
Summary of evidence from observations:
*Like charges repel, unlike attract
For point charges:
*Changing either charge changes the force proportionally. (e.g. doubling either charge doubles the force)
*The force decreases as the distance between the charges increase, and vice versa.
*The force changes quadratically with the distance (e.g. halving the distance quadruples the force)
Electrostatics
The Electric Charge
... and the rest of the cast
Electrostatics
The influence & interaction of electric charges
The Cast
q
\vec{E}
V
\Phi
\vec{F}
U
potential
potential energy
field
force
charge
flux
influence
interaction
Electric ....
Electrostatics
The influence & interaction of electric charges
The Cast - relationship map
Electric ....
\vec{E}
V
\Phi
influence
interaction
\ \vec{E}=-\vec{\nabla} V\
\ \Delta V =- \int \vec{E}\cdot d\vec{s}\
\ \Phi = \int \vec{E}\cdot d\vec{A}\
\vec{F}
U
\ \vec{F}=-\vec{\nabla} U\
\ \Delta U = -\int \vec{F}\cdot d\vec{s}\
\ \vec{F} = q_0\ \vec{E}\
\ \vec{E} = \vec{F}/q_0\ \
\ U = q_0\ V\
\ V = U/q_0\ \
q
Electrostatics
The Electric Field
and The Electric Force
Electrostatics
The Electric Field
Relationship to the Electric Force
\vec{E}
influence at some location in space
interaction between charges
\vec{F}
\ \vec{F} = q_0\ \vec{E}\
\ \vec{E} = \vec{F}/q_0\ \
Electric Field
Electric Force
Electrostatics
The Electric Field
Relationship to the Electric Force
\ \vec{F} = q_0\ \vec{E}\
\vec{E}
influence at some location in space
interaction between charges
\vec{F}
\ \vec{F} = q_0\ \vec{E}\
\ \vec{E} = \vec{F}/q_0\ \
Electric Field
Electric Force
\text{a charge $q_0$ in a local field $\vec{E}$}
\text{experiences a force $\vec{F}=q_0\vec{E}$}
\vec{E}
\vec{E}
\vec{E}
\vec{F}
\text{the force on a positive charge}
\text{is in the same direction as the field}
\text{the force on a negative charge}
\text{is in the opposite direction to the field}
\vec{F}
Electrostatics
The Electric Force
between two point-charges
Electrostatics
The Electric Force
between two point charges
q_1
q_2
\vec{E}_\text{@ P due to $q_1$}=\frac{kq_1}{r^2}\ \hat{r}
The Electric Field generated by q1 at the location P:
Another charge q2 placed at P would experience a force:
\vec{F}_\text{on a charge $q_2$ present @P}= q_2\times \vec{E}_\text{@ P due to $q_1$}
\vec{F}_\text{$q_1$ on $q_2$}=\frac{kq_1\ q_2}{r^2}\ \hat{r}_{\tiny q_1\to q_2}
Putting it together:
Electrostatics
The Electric Force
Coulomb's Law
\vec{F}_{ij}=\tfrac{1}{4\pi\epsilon_0}\frac{q_i\ q_j}{r^2_{\tiny ij}}\ \hat{r}_{\tiny ij}
\text{the electric force of $q_i$ on $q_j$}
\text{permittivity}
\text{ the distance between $q_i$ and $q_j$}
\text{ direction $i\rightarrow j$}
\text{ square}
\text{the charge exerting the force}
\text{the charge experiencing the force}
\left( k
=\frac{1}{4\pi\epsilon_0}
=8.99\times10^9
\quad \frac{\text{N$\cdot$ m$^2$}}{\text{C}^2}\right)
\epsilon_0
=8.85\times10^{-12}
\quad \frac{\text{C}^2}{\text{N$\cdot$ m$^2$}}
\text{(free-space)}
\vec{F}_{q_i \text{ on } q_j}
Electrostatics
The Electric Force
Coulomb's Law -- direction information
\vec{F}_{ij}=k\frac{q_i\ q_j}{r^2_{\tiny ij}}\ \blue{\hat{r}_{\tiny ij}}
\textcircled{\mathbf{\cdot}}
\textcircled{\cdot}
q_j
q_i
\vec{r}_{i}
\vec{r}_{j}
\text{ $\vec{r}_{ij}$ originates at $i$ and terminates at $j$}
\vec{r}_{ij}= \vec{r}_{j}-\vec{r}_{i}
\hat{r}_{ij}\text{ is a unit vector in direction of $\vec{r}_{ij}$}
\hat{r}_{ij}=\tfrac{\vec{r}_{ij}}{r_{ij}}
\hat{r}_{ji}= -\hat{r}_{ij}
\vec{r}_{ji}
= \vec{r}_{i}-\vec{r}_{j}
=-( \vec{r}_{j}-\vec{r}_{i})
=-\vec{r}_{ij}
\vec{r}_{ji}\text{ is in a direction opposite of of $\vec{r}_{ij}$}
\vec{F}_{ji}
= k\frac{q_j\ q_i}{r^2_{\tiny ji}}\ \blue{\hat{r}_{\tiny ji}}
= k\frac{q_i\ q_j}{r^2_{\tiny ij}}\ \blue{(-\hat{r}_{\tiny ij})}
=-\vec{F}_{ij}
\hat{r}_{ij}
\vec{r}_{ij}
q_i
\textcircled{\mathbf{\cdot}}
\vec{r}_{ji}
\hat{r}_{ji}
\vec{r}_{i}
\textcircled{\cdot}
q_j
\vec{r}_{j}
Electrostatics
The Electric Force
Coulomb's Law -- attraction & repulsion
q_j
q_i
\vec{F}_{ij}=k\frac{\blue{q_i\ q_j}}{r^2_{\tiny ij}}\ {\hat{r}_{\tiny ij}}
q_i\ q_j\gt 0
q_i\ q_j\lt 0
q_j
q_i
q_j
q_i
q_i
q_j
\vec{F}_{ij}
\vec{F}_{ij}
\vec{F}_{ij}
\vec{F}_{ij}
\hat{r}_{ij}
\hat{r}_{ij}
\hat{r}_{ij}
\hat{r}_{ij}
q_j
q_i
\hat{r}_{ij}
\vec{r}_{ij}
Electrostatics
The Electric Force
The net Electric Force due to a configuration of charges
Electrostatics
The Electric Force
Coulomb's Law
\textcircled{\mathbf{+}}
\textcircled{-}
\textcircled{+}
\textcircled{-}
For a given configuration of point charges
q_1
q_2
q_4
q_3
Electrostatics
The Electric Force
Coulomb's Law
\textcircled{\mathbf{+}}
q_1
\textcircled{-}
\textcircled{+}
q_2
\textcircled{-}
q_4
q_3
The interaction can be described in terms of force-pairs
\text{the electric force}
\text{of $q_4$ on $q_2$}
\text{the electric force}
\text{of $q_2$ on $q_4$}
Electrostatics
The Electric Force
Coulomb's Law
\textcircled{-}
q_4
The net electric force on a charge of interest is the vector sum of all the electric forces acting on it.
\text{the electric force}
\text{of $q_2$ on $q_4$}
\textcircled{-}
q_4
\text{the electric force}
\text{the electric force}
\text{of $q_1$ on $q_4$}
\Sigma\vec{F}_\text{on $q_4$}
\vec{F}_\text{$q_1$ on $q_4$}
\vec{F}_\text{$q_2$ on $q_4$}
\vec{F}_\text{$q_3$ on $q_4$}
=
+
+
\text{of $q_3$ on $q_4$}
\Sigma \vec{F}_\text{on $q_4$}
\vec{F}_\text{$q_1$ on $q_4$}
\vec{F}_\text{$q_2$ on $q_4$}
\vec{F}_\text{$q_3$ on $q_4$}
Electrostatics
The Electric Force
Coulomb's Law -- Check your understanding
Three identical small spheres are fixed on the vertices of an equilateral triangle whose side is [d] cm in length. The spheres at vertices A and B carry negative excess charges, qA and qB, respectively. The sphere at vertex C carries excess positive charge, qC.
Suppose that qA=qB, what is the magnitude and direction of the net electric force on the sphere at C due to the charges at A and B.
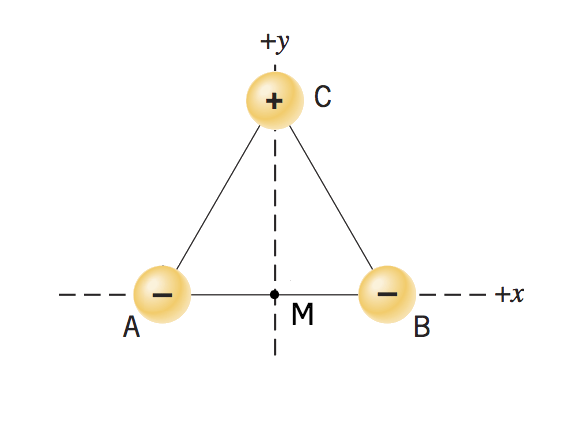
The force on C due to the combined effect of A and B is the vector sum of the forces on C due to A, and on C due to B:
\vec{F}_\text{on C due to A and B} = \vec{F}_\text{on C due to A} + \vec{F}_\text{on C due to B}
The magnitude of each of the forces is given by Coulomb's law. However, since these forces are pointing in different directions, the only way to find their resultant is by vector addition:
Due to the symmetry, the x components of the forces are going to cancel each other because they would be equal and opposite. The y components would add:
(F_\text{on C due to A and B})_x = - \frac{k\ q_A\ q_C}{r^2_{AC}} \cos{60^\circ } + \frac{k\ q_B\ q_C}{r^2_{BC}} \cos{60^\circ } = - \frac{k\ q\ q_C}{d^2} \cos{60^\circ } + \frac{k\ q\ q_C}{d^2} \cos{60^\circ }=0
(F_\text{on C due to A and B})_y = - \frac{k\ q_A\ q_C}{r^2_{AC}} \sin{60^\circ } - \frac{k\ q_B\ q_C}{r^2_{BC}} \sin{60^\circ } = - \frac{k\ q\ q_C}{d^2} \sin{60^\circ } - \frac{k\ q\ q_C}{d^2} \sin{60^\circ }=- 2\ \frac{k\ q\ q_C}{d^2} \sin{60^\circ }
Electrostatics
The Electric Force
Coulomb's Law -- Check your understanding
\textcircled{\mathbf{+}}
\textcircled{-}
\textcircled{+}
\textcircled{-}
q_1
q_2
q_4
q_3
Electric Force
By drmoussaphysics
