Breaking RSA
Cesena Security Network and Application
hard as solving the factoring problem
Asymmentric Key Cryptography
or Public-Key Cryptography

- RSA algorithm was publicated by Rivest, Shamir, Adleman
- Diffie and Hellman introduced public-key cryptography in 1976 (using RSA)
- The two keys are use to encrypt (public) and decrypt the data (private)
- Based on mathematical calculation
Text
Key Generation
- Choose two prime number p and q
- Compute n = p * q
- Compute:
- Choose an integer e s.t. 1 < e < λ(n) and gcd(e, λ(n)) = 1
- Determine d as d * e ≡ 1 * mod(λ(n)):
- d is used as the private key exponent
- e is used as the public key exponent
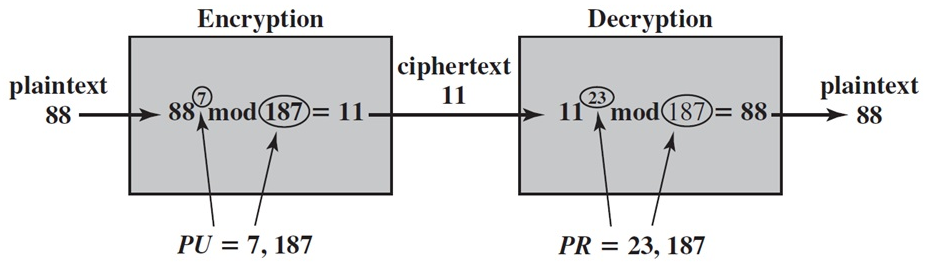
How it works?
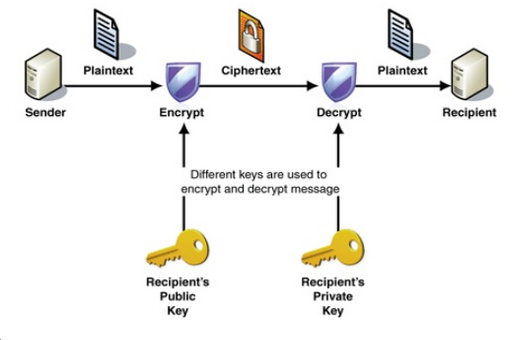
- Alice shares securly her public key
- Bob can pick up the her public key
- Bob (the sender) use the Alice's public key to encrypt the message
- Alice and only Alice can decrypt the message with her private key
Encryption
Decryption
n = p * q
Confidentiality vs Authentication
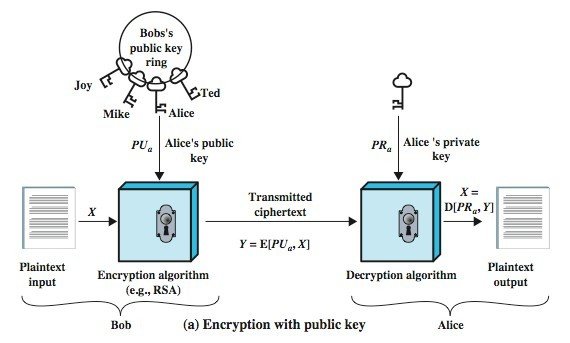
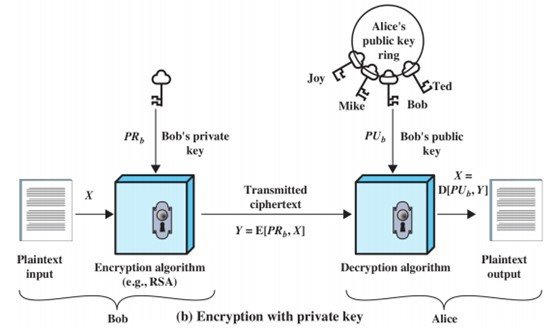
Confidentiality vs Authentication

Use Case
- Mail (GPG)
- Web (SSL, TLSv1.{1,2,3})
- VPN
- Ransomware
- Secure VOIP
- SSH
- BitCoin
Breaking RSA Security
- n : public key
- p , q : private factors of n = p.q
- ϕ(n) : Euler’s totient function, here ϕ(n) = (p − 1).(q − 1)
- e : public encryption or signature exponent
- d : private encryption or signature exponent
- e.d ≡ 1 mod ϕ(N) relatioship between public and private
- exponent
- c ≡ m e mod N : encrypted message
- m ≡ c d mod N : decrypted message
- Finding d , ϕ(n) or p is enough to crack RSA security
RSA Challenge
RSA-1024 with 309 modulus digits -> 100.000 $
In 2009, to factor a 232-digit number (RSA-768) utilizing hundreds of machines took two years and the researchers estimated that a 1024-bit RSA modulus would take about a thousand times as long. However, it has not been proven that no efficient algorithm exists.
Tools
yafu - Automated integer factorization
https://github.com/DarkenCode/yafu
??SINGLE CORE??
120 digits -> still running after 4 hours...
cado-nfs
https://gforge.inria.fr/scm/?group_id=2065
CADO-NFS is a complete implementation in C/C++ of the Number Field Sieve (NFS) algorithm for factoring integers. It consists in various programs corresponding to all the phases of the algorithm, and a general script that runs them, possibly in parallel over a network of computers.
| Input Number | cado-nfs 2.2.0 [hours] |
|---|---|
| RSA-120 | 2.2 |
| RSA-130 | 8.2 |
| RSA-140 | 30.9 |
| RSA-155 | 5.8 [days] |
Xeon(R) CPU E5-2650 at 2.00GHz, 8 process with 2 thread each
CUDA??

Attacks
- MiTM during key exchange
- Bad key generation with custom or bugged tools: small factors, common factors, reused factors, weak entropy
- GCD for lots of shared public keys
- Fermat is p and q are close
- ECM (sub-exponential running time algorithm for integer factorization which employs elliptic curves)
- Wiener
- Bad algorithm applications (Chinese Remainder Theorem)
- Known-plaintext attack (only for weak signatures)
- Number Field Sieve complex but very parallelizable
- Quantum algorithm: O((log N)^3)) !
- Side channel (power consumption, social engineering, theft, exploit, ...)

Bruteforce n using Fermat or Miller Rabin
with Rust
MillerRabin(n)
If n > 2 and n is even
return composite.
/* Factor n−1 as 2^s * t where t is odd. */
s ← 0
t ← n − 1
while t is even
s ← s + 1
t ← t/2
end
/* Done. n − 1 = 2^s * t. */
Choose x∈{1,2,...,n−1} uniformly at random.
Compute each of the numbers x^t,x^(2t),x^(4t),...,x^(2st) = x^(n−1) mod n.
If x^(n−1) !≡ 1 (mod n)
return composite.
for i = 1,2,...,s
If x^(2^i *t) ≡ 1 (mod n) and x^(2^(i-1) * t) !≡ ± 1 (mod n)
return composite.
end
/* Done checking for fake square roots. */
Return probably primeIf p is an odd prime number, and p – 1 = 2^s * d, with d odd, then for every a prime to p, either ad ≡ 1 mod p, or there exists t such that 0 ≤ t < s and a2td ≡ −1 mod p
Fermat Little Theorem
If p is a prime number, then for any integer a, the number a * p − a is an integer multiple of p. In the notation of modular arithmetic, this is expressed as
Pick random a that is not divisible by p and see whether the equality holds. If the equality does not hold for a value of a, then p is composite.
Therefore, if the equality does hold for one or more values of a, then we say that p is probably prime.
Disclaimer
yes... again math....
The observabale universe contains about 10⁸⁰ atoms. Assume that we could leverage every single atom as a CPU, and each CPU could enumerate 1.000.000
(I mean: HOLY SHIT!) RSA keys per second.
The number of primes smaller than an integer n is approximately n/log(n).
Disclaimer
The number of primes smaller than an integer n is approximately n/log(n).
yes... again math....

The observabale universe contains about 10⁸⁰ atoms. Assume that we could leverage every single atom as a CPU, and each CPU could enumerate 1.000.000
(I mean: HOLY SHIT!) RSA keys per second.
The Big Bang occurred 13.8 * 10⁹ years ago.
Bruteforce using Rust
Results
PayPal site have a public key with 617 digits...

Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz
| Input Number Length | rsa-rust [seconds] |
|---|---|
| 7 | 0 |
| 13 | 0 |
| 19 | 97 (*) |
| 29 | up to 15 hours (*) |
| 120 | impossibru |
Duplicate primes using GCD
Factorization is hard but there is way to discover p and q: Greatest Common Divisor
gcd(10, 30) = 10 gcd(100, 144) = 4 gcd(3, 7) = 1
gcd(p, q) = 1
In [11]: %%time
...: gmpy2.gcd(1066887566150220425445511836658004853426772855284443812385956279691811153210420393206090450561091324583700261488330797336274357210036391729479838797536785423621,
...: 121766994908646736104647201413197886828038168507699680036860497074009374138321196080535007864705376861476504466988251202805423843507051323234232179224638179315321450535646374123533)
...:
CPU times: user 0 ns, sys: 0 ns, total: 0 ns
Wall time: 20.7 µs
Out[11]: mpz(1)!!!!!!! 20.7 µs !!!!!!!
Duplicate primes using GCD
- Select four primes number: a, b, c ,d
- Create a public key n1 = a * b
- Create another pubic key n2 = c * d
Find the gcd(n1, n2)
Duplicate primes using GCD
- Select four primes number: a, b, c ,d
- Create a public key n1 = a * b
- Create another pubic key n2 = c * d
Find the gcd(n1, n2)
1
Not Good!! When don't know anything about a, b, c or d!
FUCK YOU RSA!!
Duplicate primes using GCD
- Select four primes number: a, b, c ,d
- Create a public key n1 = a * b
- Create another pubic key n2 = c * d
Find the gcd(n1, n2)
1
Not Good!! When don't know anything about a, b, c or d!
FUCK YOU RSA!!
What if we use only three prime number to create two publick keys?
Duplicate primes using GCD
- Select three primes number: a, b, c
- Create a public key n1 = a * b
- Create another pubic key n2 = b * c
Find the gcd(n1, n2)
Duplicate primes using GCD
- Select three primes number: a, b, c
- Create a public key n1 = a * b
- Create another pubic key n2 = b * c
Find the gcd(n1, n2)
BINGO!!!!!
The "vulnerablity" is due to faulty random number generators and/or low system entrophy used to generate RSA keys. In 2012 about 0.2% of all REAL public keys seemed to be vulnerable.
In [1]: import gmpy2
In [2]: n1 = 2477 * 577
In [3]: n2 = 577 * 1021
In [4]: %%time
...: gmpy2.gcd(n1, n2)
...:
CPU times: user 0 ns, sys: 0 ns, total: 0 ns
Wall time: 8.58 µs
Out[4]: mpz(577)Breaking RSA
By Edoardo Rosa
Breaking RSA
- 2,403



