Towards A New Era of Self-Supervised Representation Learning for Astrophysics
Francois Lanusse
- 1000 images each night, 15 TB/night for 10 years
- 18,000 square degrees, observed once every few days
- Tens of billions of objects, each one observed ∼1000 times
SDSS
Image credit: Peter Melchior
DES
Image credit: Peter Melchior
Image credit: Peter Melchior
HSC (proxy for LSST)
The Deep Learning Boom in Astrophysics
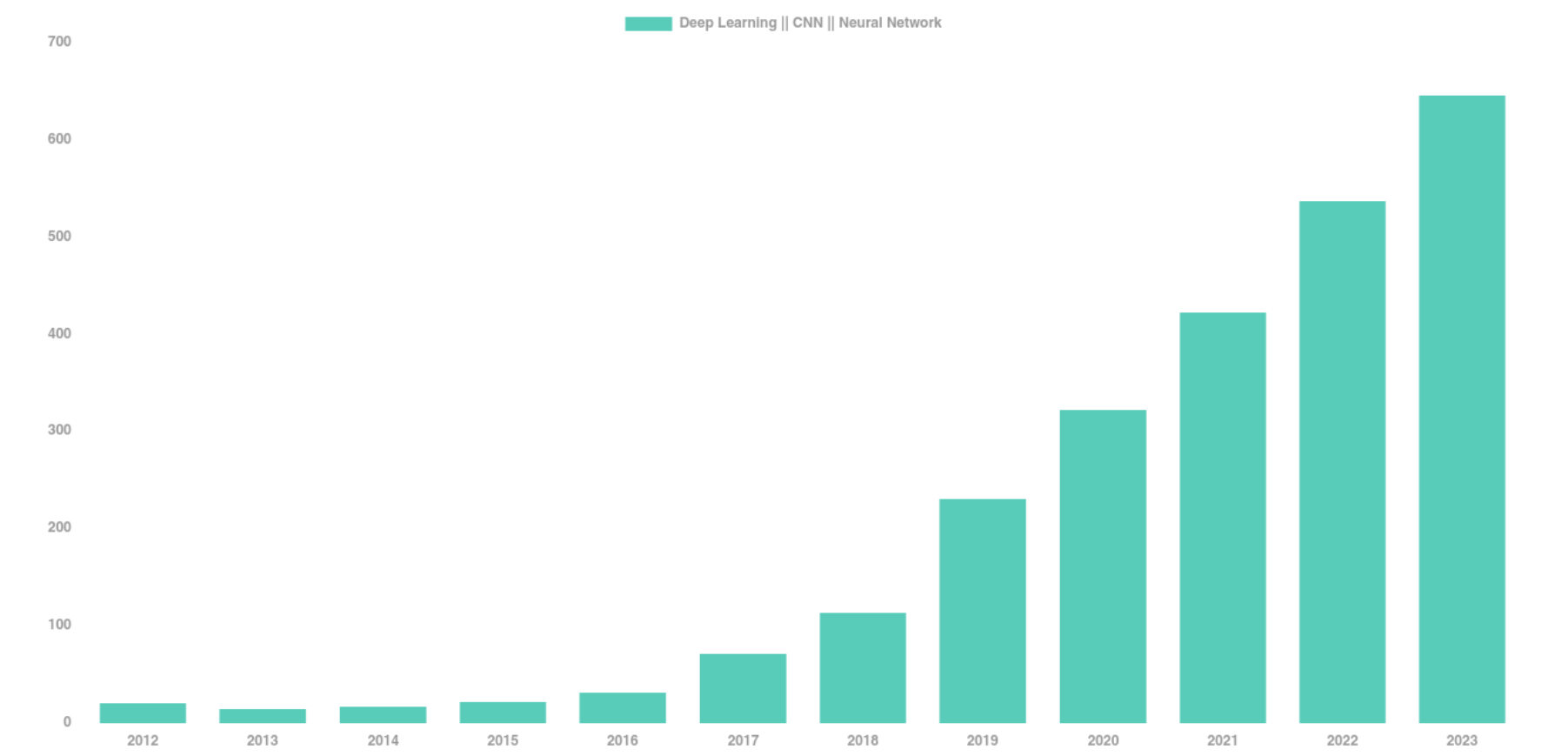
astro-ph abstracts mentioning Deep Learning, CNN, or Neural Networks
The vast majority of these results has relied on supervised learning and networks trained from scratch.
The Limits of Traditional Deep Learning
-
Limited Supervised Training Data
- Rare or novel objects have by definition few labeled examples
- In Simulation Based Inference (SBI), training a neural compression model requires many simulations
- Rare or novel objects have by definition few labeled examples
-
Limited Reusability
- Existing models are trained supervised on a specific task, and specific data.
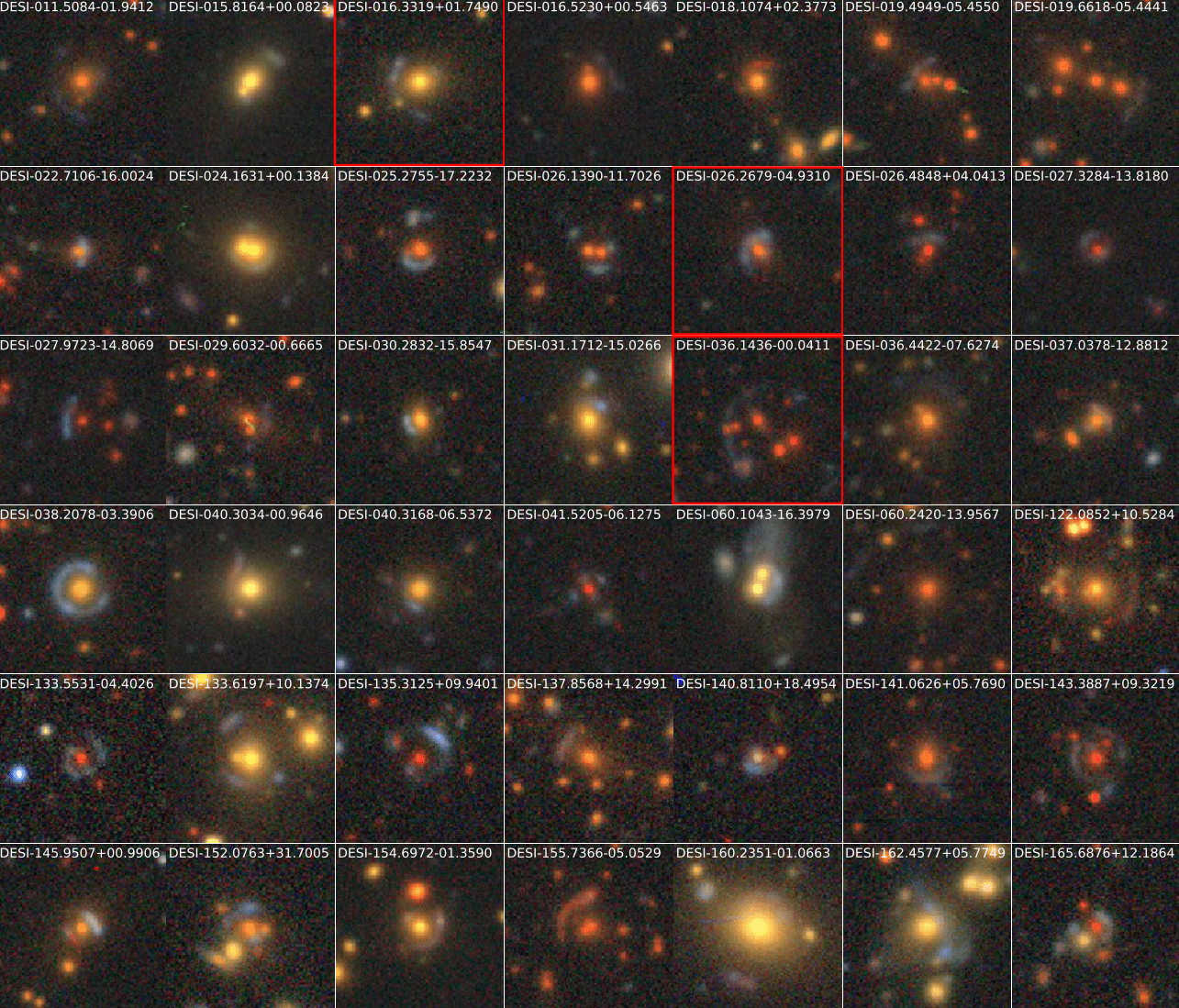
=> Limits in practice the ease of using deep learning for analysis and discovery
Meanwhile, in Computer Science...
The Rise of The Foundation Model Paradigm
-
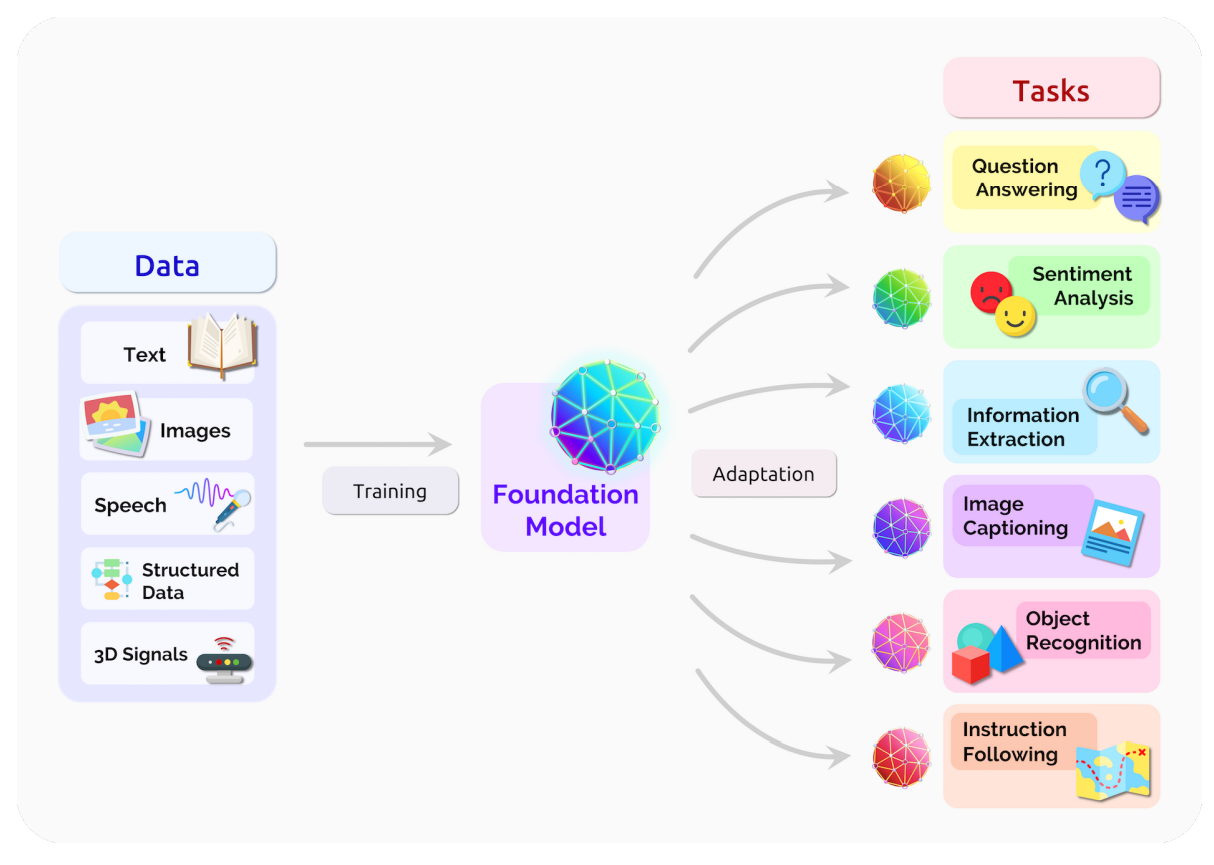
Foundation Model approach
- Pretrain models on pretext tasks, without supervision, on very large scale datasets.
- Adapt pretrained models to downstream tasks.
- Combine pretrained modules in more complex systems.
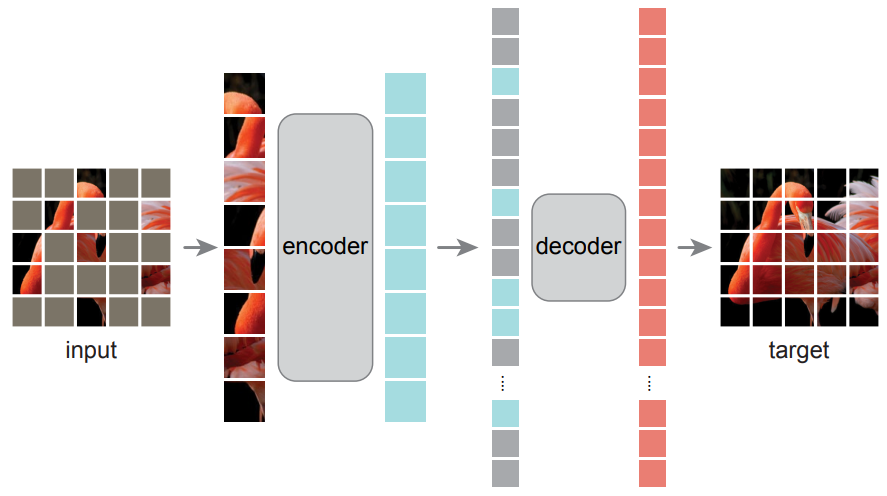
The Advantage of Scale of Data and Compute
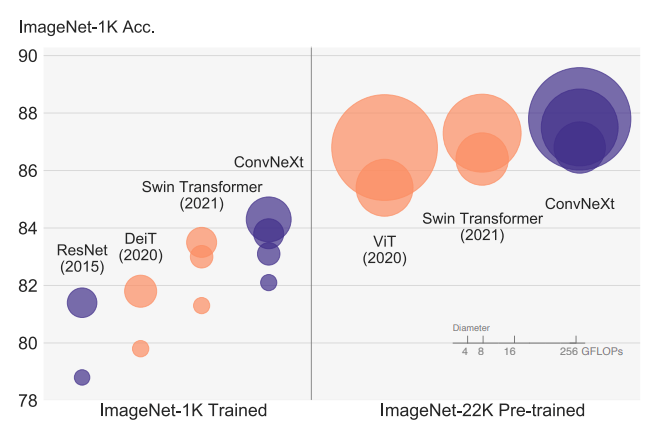
Linearly Accessible Information
- Backbone of modern architectures embed input images as vectors in where d can typically be between 512 to 2048.
- Linear probing refers to training a single matrix to adapt this vector representation to the desired downstream task.
\mathbb{R}^{d}
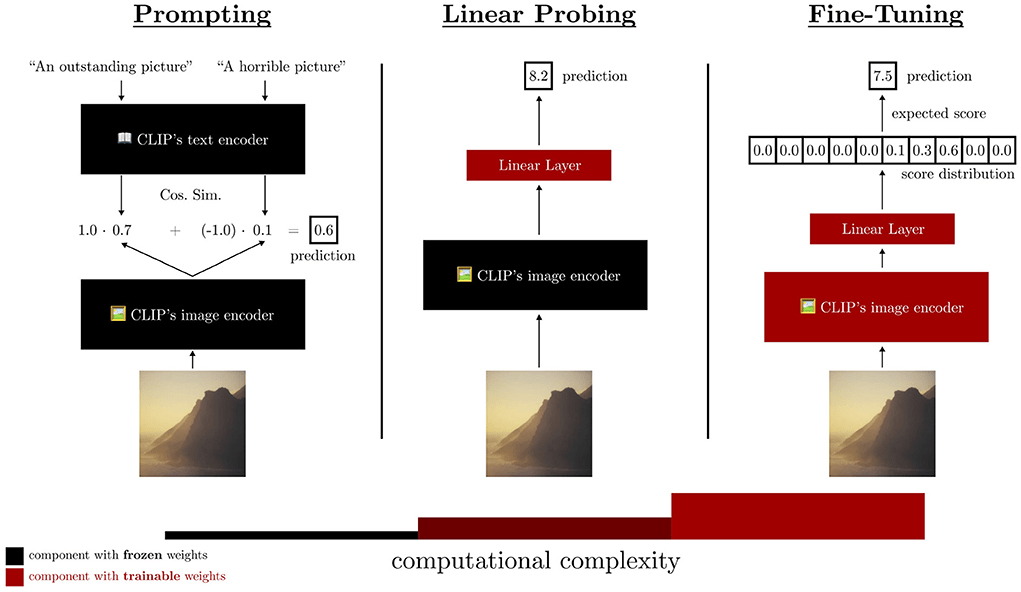
What This New Paradigm Could Mean for Us
-
Never have to retrain my own neural networks from scratch
- Existing pre-trained models would already be near optimal, no matter the task at hand
-
Saves a lot of time and energy
- Practical large scale Deep Learning even in very few example regime
- Searching for very rare objects in large surveys like Euclid or LSST becomes possible
-
Pretraining on data itself ensures that all sorts of image artifacts are already folded in the training.
- If the information is embedded in a space where it becomes linearly accessible, very simple analysis tools are enough for downstream analysis
- In the future, survey pipelines may add vector embedding of detected objects into catalogs, these would be enough for most tasks, without the need to go back to pixels
AstroCLIP
Cross-Modal Pre-Training for Astronomical Foundation Models
Project led by Francois Lanusse, Liam Parker, Siavash Golkar, Miles Cranmer
Accepted contribution at the NeurIPS 2023 AI4Science Workshop
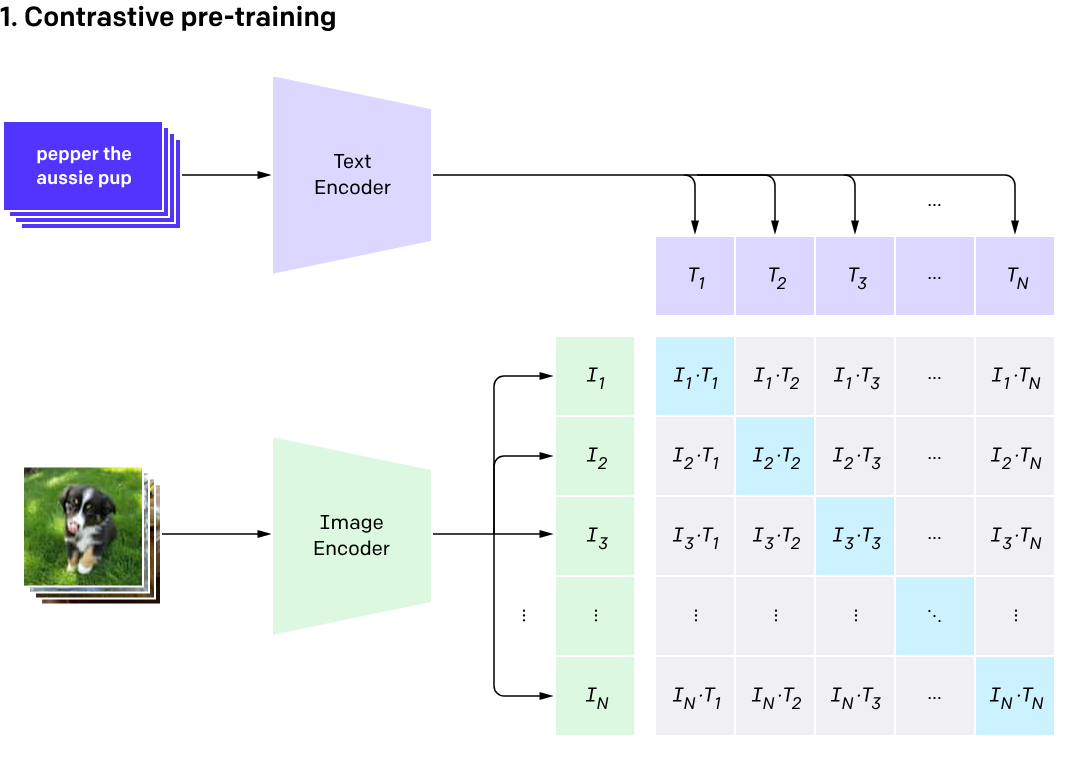
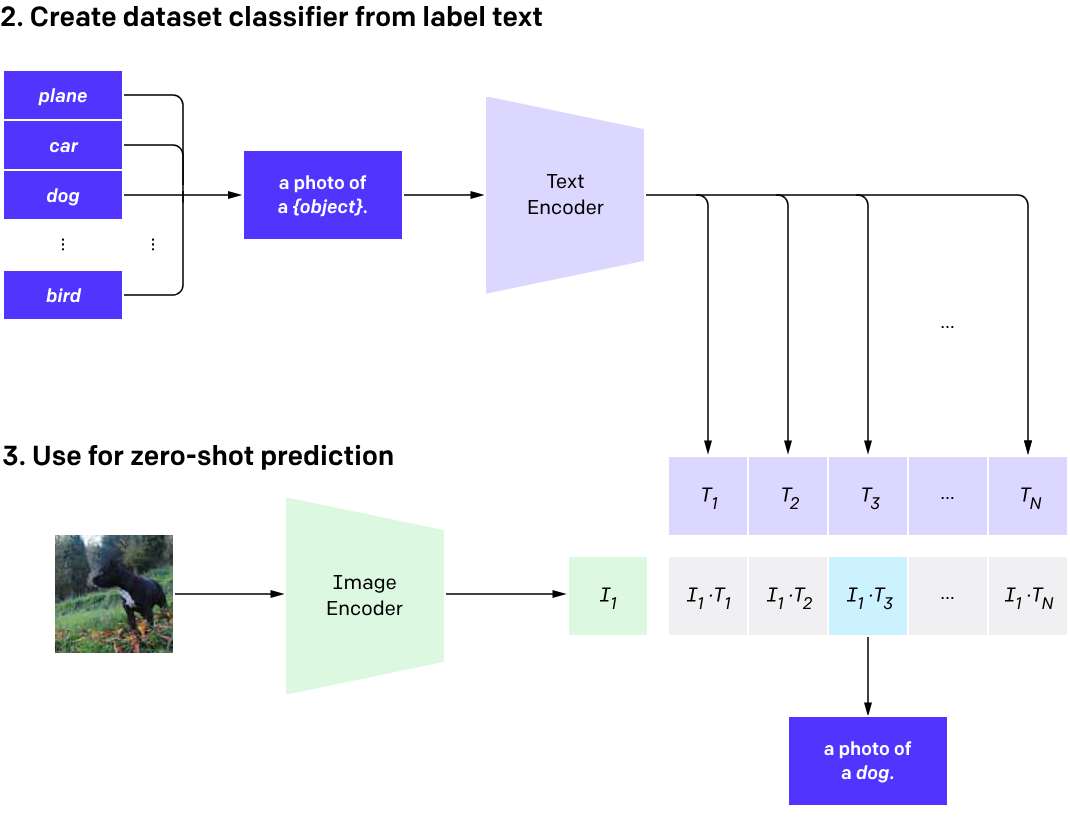
What is CLIP?
Contrastive Language Image Pretraining (CLIP)
(Radford et al. 2021)
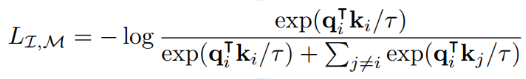
One model, many downstream applications!
Flamingo: a Visual Language Model for Few-Shot Learning (Alayrac et al. 2022)
Hierarchical Text-Conditional Image Generation with CLIP Latents (Ramesh et al. 2022)
The AstroCLIP approach
- We use spectra and multi-band images as our two different views for the same underlying object.
- DESI Legacy Surveys (g,r,z) images, and DESI EDR galaxy spectra.
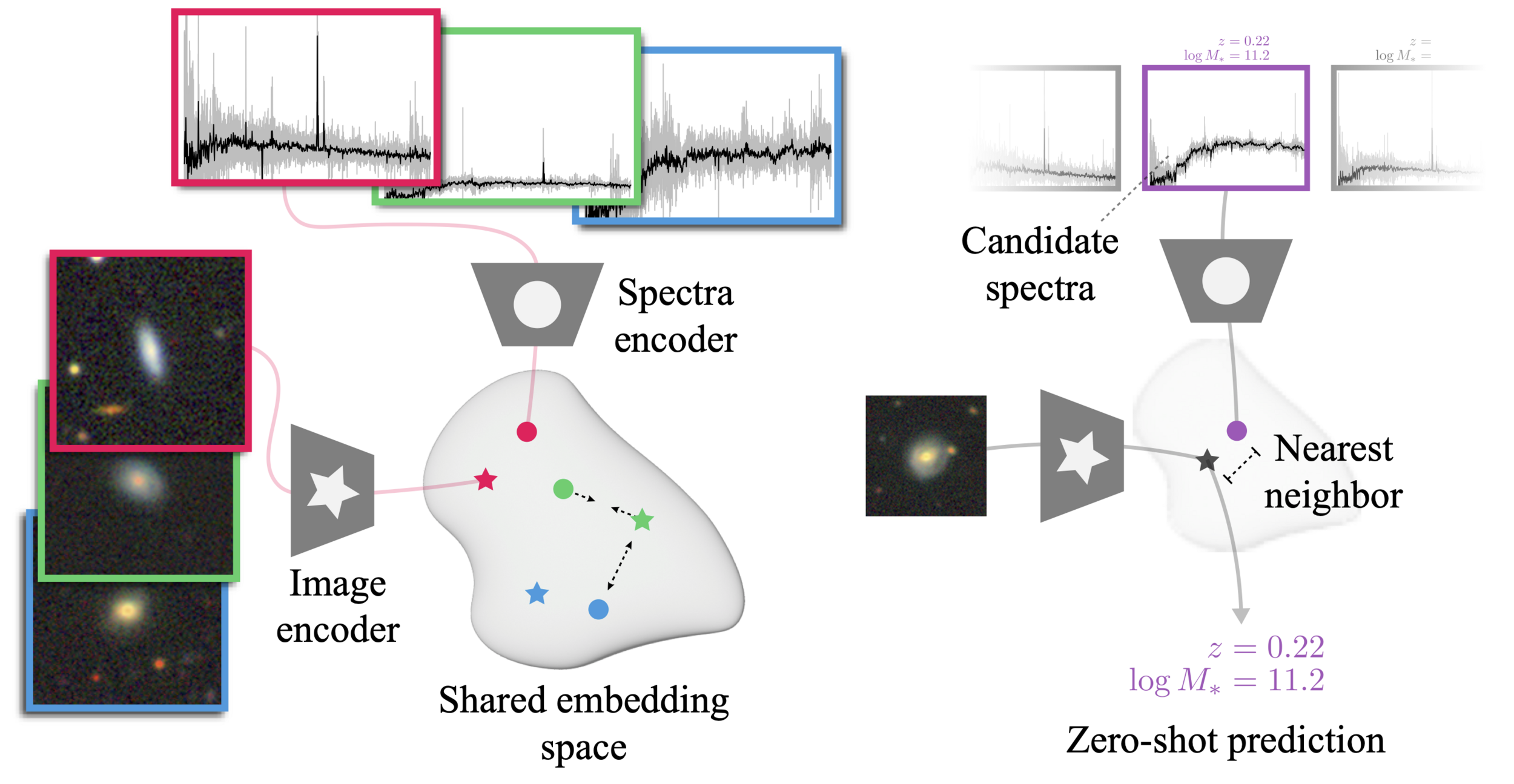
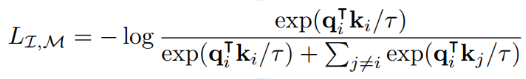
Cosine similarity search
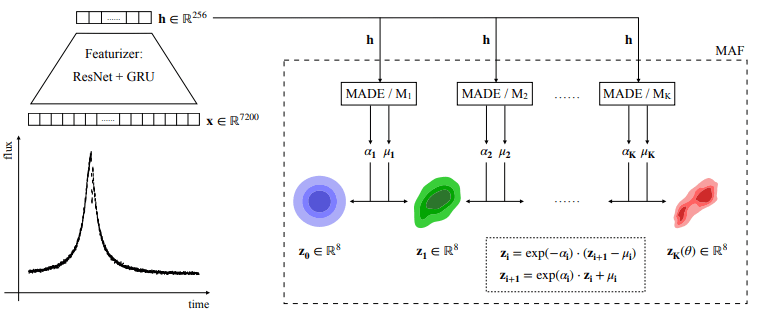
The AstroCLIP Model (v2, Parker et al. in prep.)
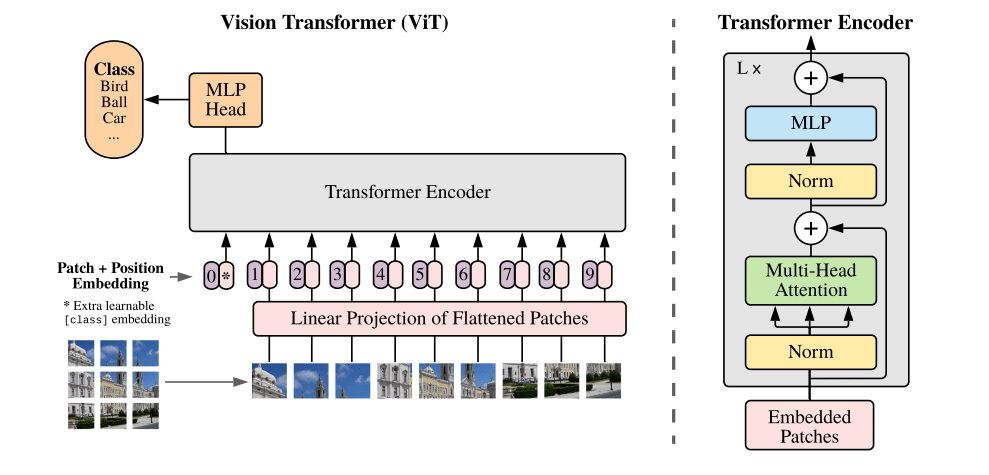
- For images, we use a ViT-L Transformer.
- For spectra, we use a decoder only Transformer working at the level of spectral patches.
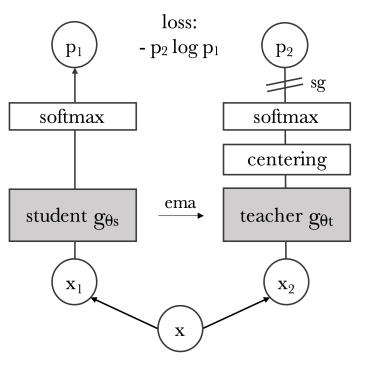
DiNOv2 (Oquab et al. 2023) Image Pretraining
- Common practice for SOTA CLIP models is to initially pretrain the image encoder before CLIP alignment
- We adopt the DiNOv2 state of the art Self-Supervised Learning model for the initial large scale training of the model.
- We pretrain the DiNOv2 model on ~15 million postage stamps from DeCALS
PCA of patch features
Dense Semantic Segmentation
Dense Depth Estimation
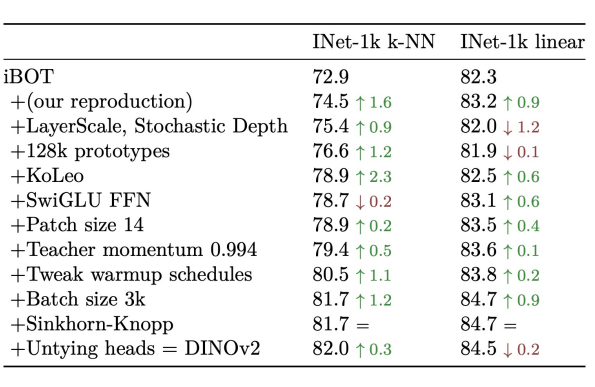
Spectrum Transformer Pretraining by Masked Modeling
- To pretrain the spectrum embedder, we use a simple Masked Image Modeling strategy
\mathcal{L}_{\textrm{MM}} = \frac{1}{NK} \sum_{j=1}^K \sum_{i=1}^N \textbf{m}_i \cdot (\textbf{x}_{i} - \hat{\textbf{x}}_{i})^2,
Evaluation of the model
- Cross-Modal similarity search
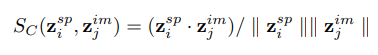
Image Similarity
Spectral Similarity
Image-Spectral Similarity
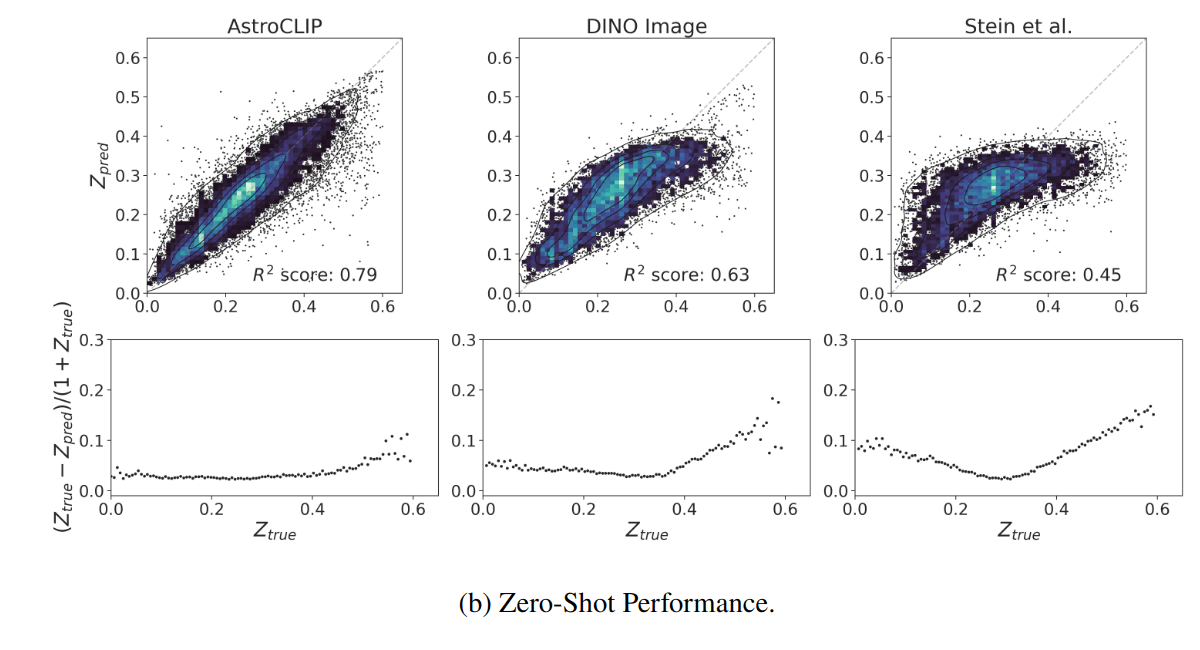
- Redshift Estimation From Images
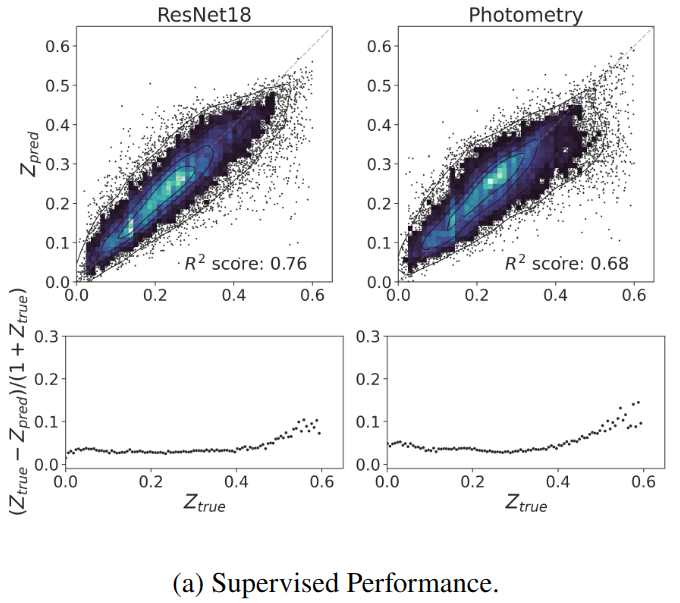
Supervised baseline
z_{true}
z_{true}
z_{true}
z_{true}
z_{true}
z_{true}
z_{true}
z_{true}
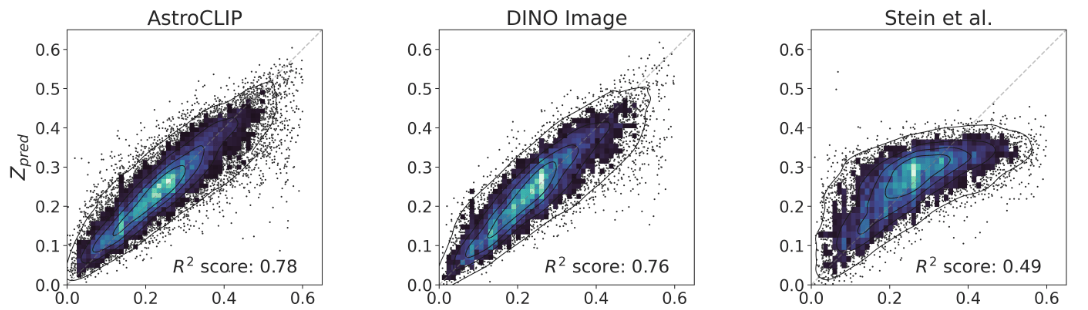
- Zero-shot prediction
- k-NN regression
- Few-shot prediction
- MLP head trained on top of frozen backbone
- Galaxy Physical Property Estimation from Images and Spectra
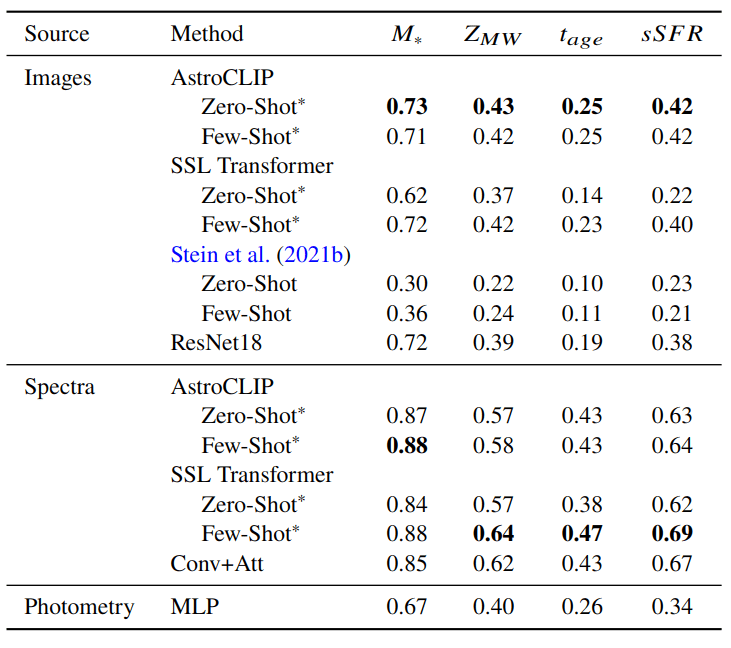
We use estimates of galaxy properties from the PROVABGS catalog (Hahn et al. 2023) (Bayesian spectral energy distribution (SED) modeling of DESI spectroscopy and photometry method)
R^2
of regression
Negative Log Likelihood of Neural Posterior Inference
- Galaxy Morphology Classification
Classification Accuracy
We test a galaxy morphology classification task using as labels the GZ-5 dataset (Walmsley et al. 2021)
How is this different from other embedding approaches?
Deep Representation Learning In Astrophysics
Most works so far have relied on (Variational) Auto-Encoders
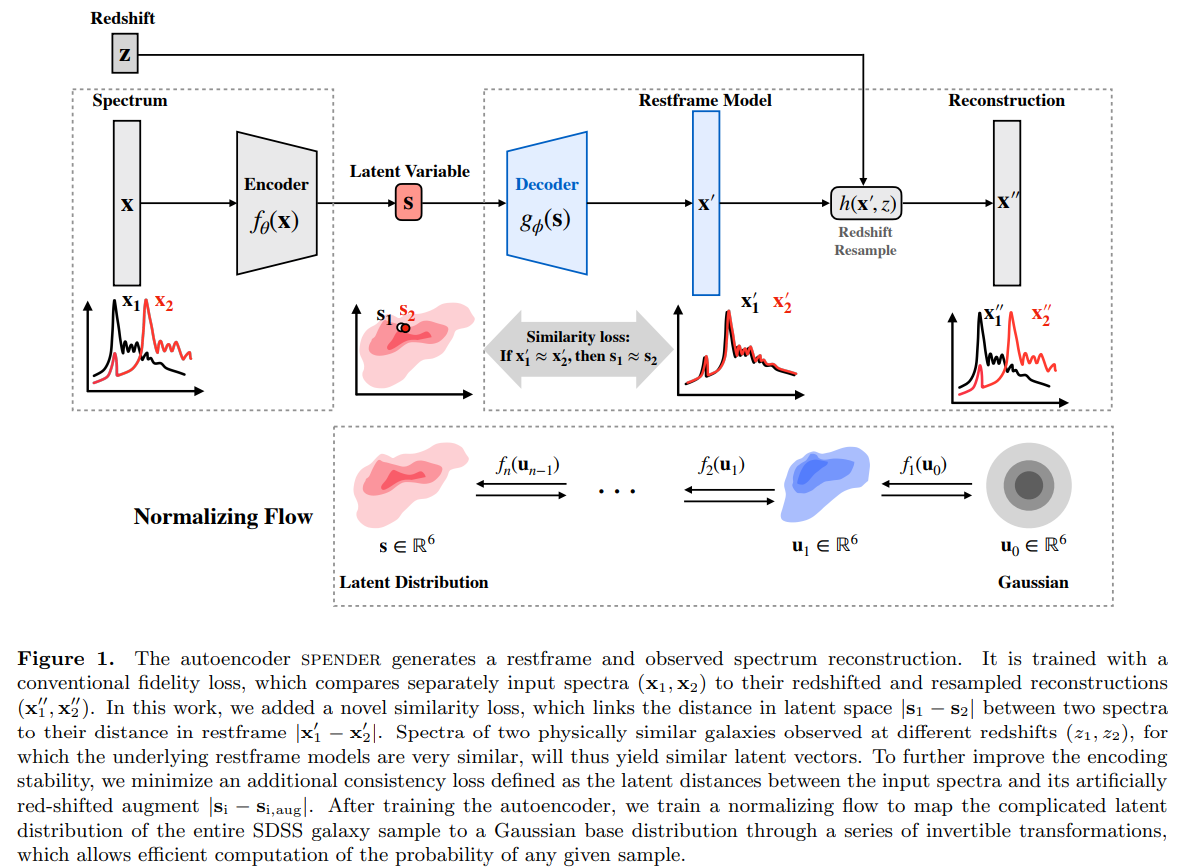
Autoencoding Galaxy Spectra II: Redshift Invariance and Outlier Detection (Liang et al. 2023)
A few comments on this approach
- Building an informative latent space relies on introducing an arbitrary information bottleneck:
- Too big, no structure emerges
- Too small, information is lost
- There is no constraint that the latent space should be well behaved
- Many ad-hoc schemes exist such as beta-VAE to force disentanglement
- Many ad-hoc schemes exist such as beta-VAE to force disentanglement
- More philosophically, this is a generative modeling approach
- We don't necessarily need to reconstruct a full observation to extract useful information about it.
Contrastive Learning in Astrophysics
Self-Supervised similarity search for large scientific datasets (Stein et al. 2021)
Detecting Galaxy Tidal Features Using Self-Supervised Representation Learning
Project led by Alice Desmons, Francois Lanusse, Sarah Brough
A Few Words on Theory and Empirical Observations
The Information Point of View
- The InfoNCE loss is a lower bound on the Mutual Information between modalities
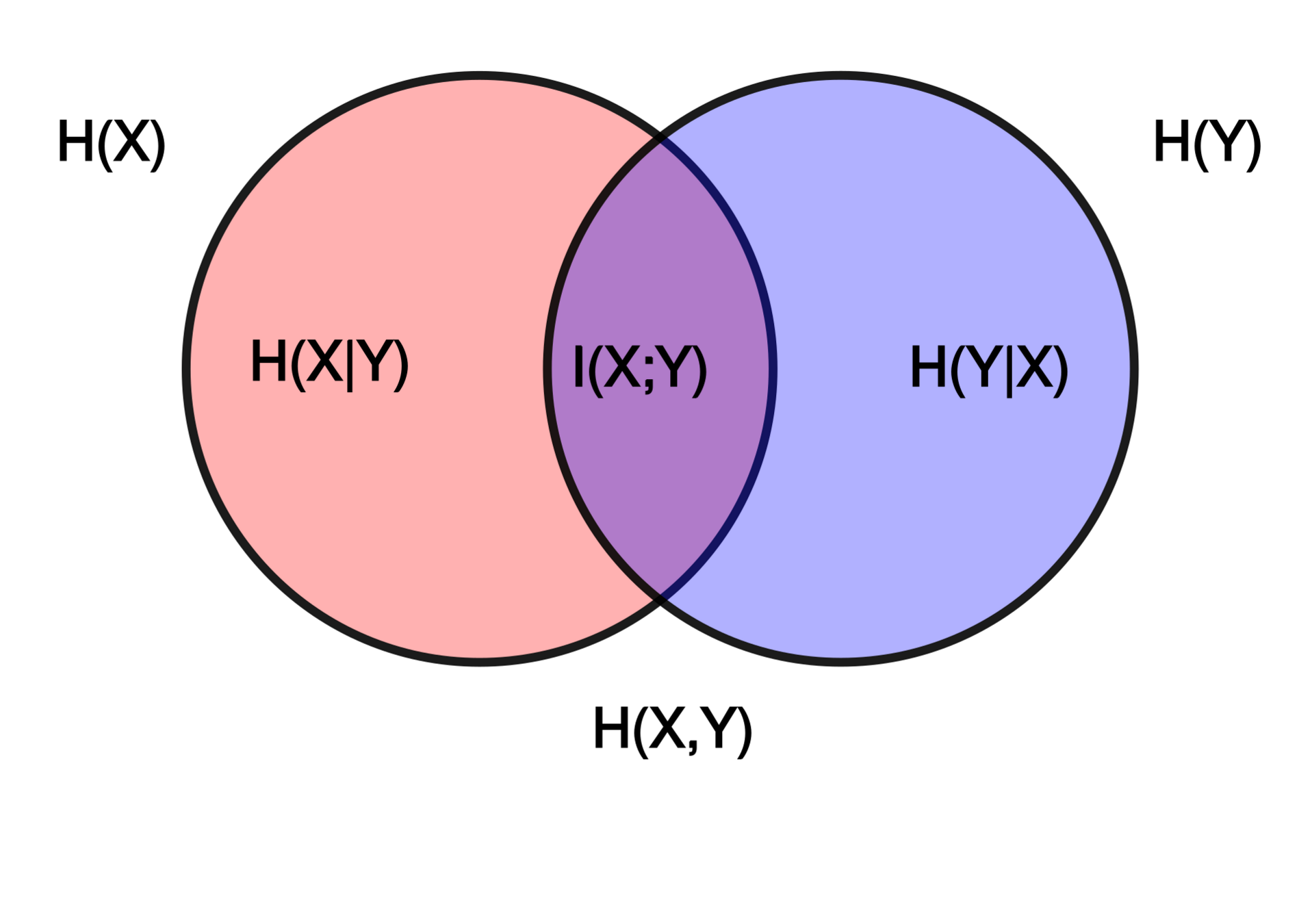
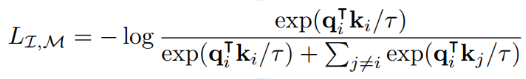
Shared physical information about galaxies between images and spectra
Thinking about data from a hierarchical Bayesian model point of view
y \sim \underbrace{p_{obs}( y | x )}_{\text{instrument specific}} \qquad \underbrace{p(x | \theta)}_{\text{generative process}} \qquad \underbrace{p(\theta)}_{\text{physical parameters}}
=> We are building summary statistics for the physical parameters describing an object in a completely data driven way
A Surprising Observation
Redshift information in image embedding
Redshift information in spectra embedding
=> We find in practice that our contrastive alignment behave similarly to Canonical Correlation Analysis
What comes next!
- Idea of finding a common shared representation diverse observational modalities
- Next steps would be, embedded data from different instruments, different filters, etc... to build a universal embedding for types of galaxy observations
Polymathic
Towards Large Multi-Modal Observational Models
Most General
Most Specific
Independent models for every type of observation
Single model capable of processing all types of observations
Towards Large Multi-Modal Observational Models
Most General
Most Specific
Independent models for every type of observation
Single model capable of processing all types of observations
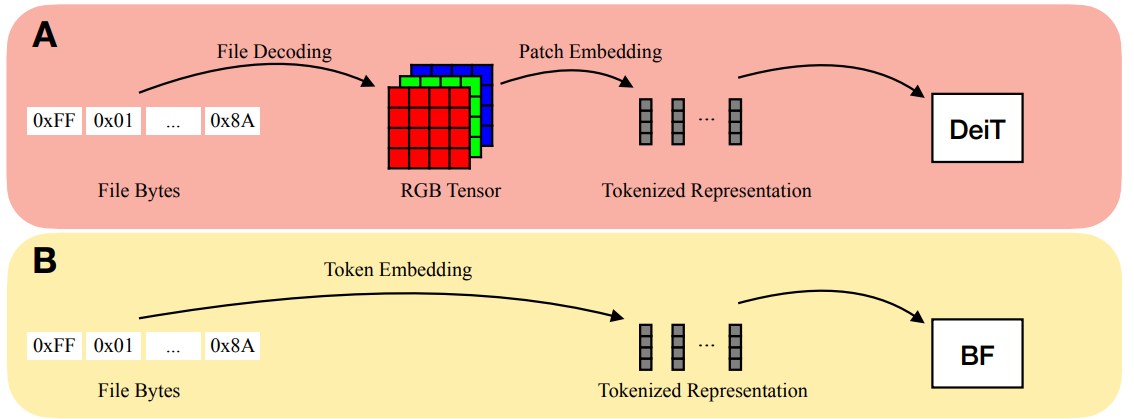
Bytes Are All You Need (Horton et al. 2023)
Towards Large Multi-Modal Observational Models
Most General
Most Specific
Independent models for every type of observation
Single model capable of processing all types of observations
Bytes Are All You Need (Horton et al. 2023)
AstroCLIP
Follow us online!
Thank you for listening!
Towards Self Supervised Representation Learning
By eiffl
