Intro to Self-Supervised Representation Learning for Astrophysics

Francois Lanusse



- 1000 images each night, 15 TB/night for 10 years
- 18,000 square degrees, observed once every few days
- Tens of billions of objects, each one observed ∼1000 times
SDSS
Image credit: Peter Melchior
DES
Image credit: Peter Melchior
Image credit: Peter Melchior
HSC (proxy for LSST)
The Deep Learning Boom in Astrophysics
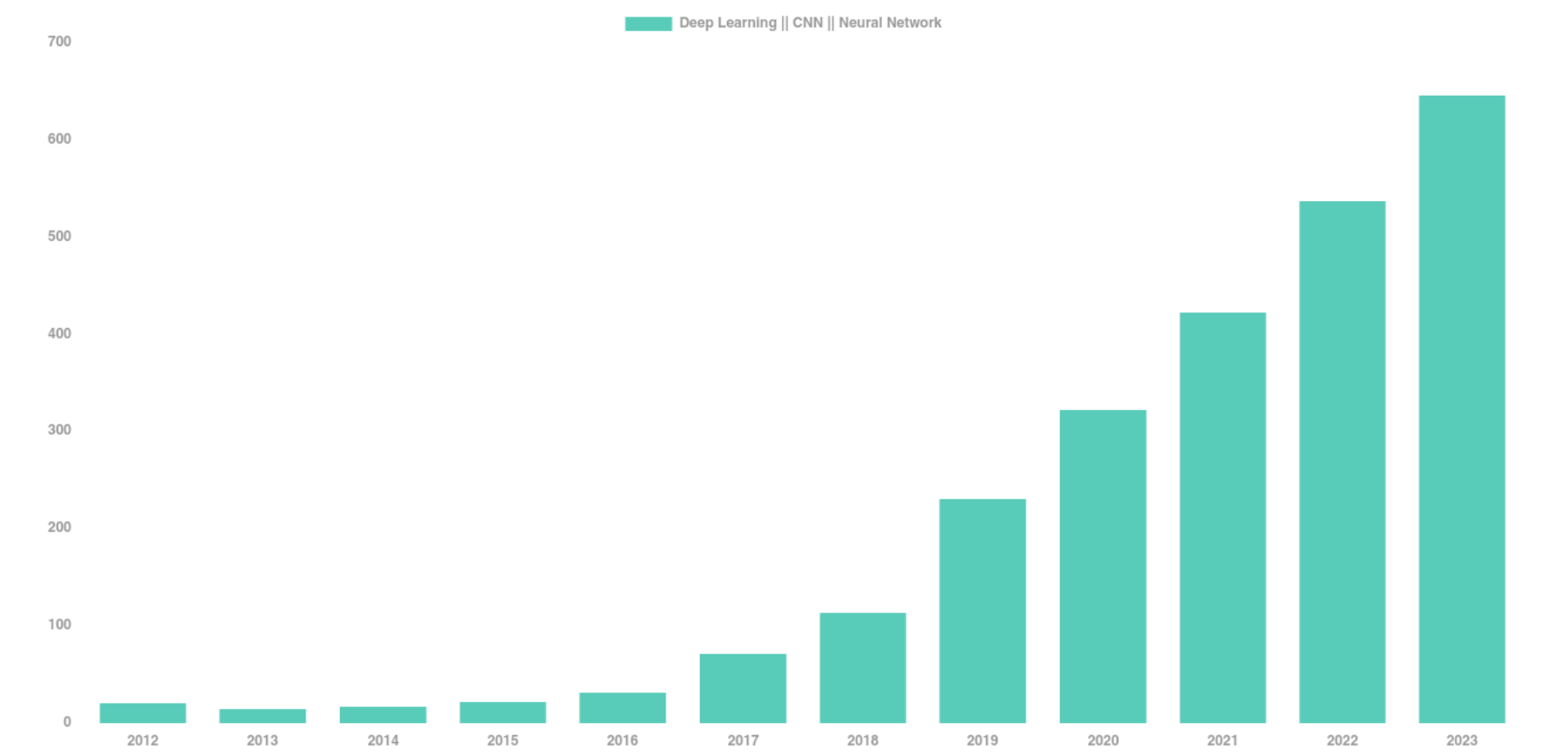
astro-ph abstracts mentioning Deep Learning, CNN, or Neural Networks
The vast majority of these results has relied on supervised learning and networks trained from scratch.
The Limits of Traditional Deep Learning
-
Limited Supervised Training Data
- Rare or novel objects have by definition few labeled examples
- In Simulation Based Inference (SBI), training a neural compression model requires many simulations
- Rare or novel objects have by definition few labeled examples
-
Limited Reusability
- Existing models are trained supervised on a specific task, and specific data.
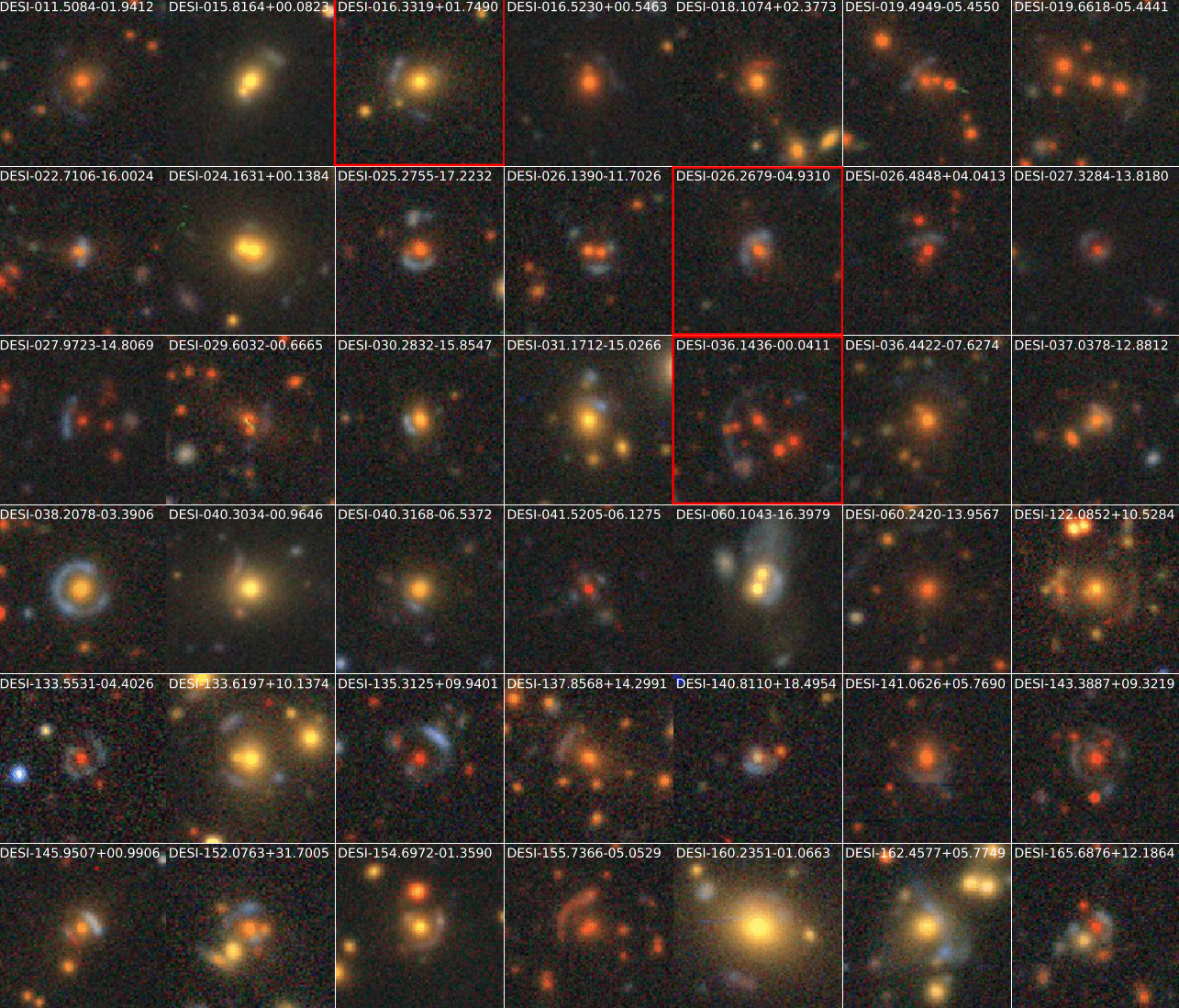
=> Limits in practice the ease of using deep learning for analysis and discovery
Can we make use of all the unlabeled data we have access to?
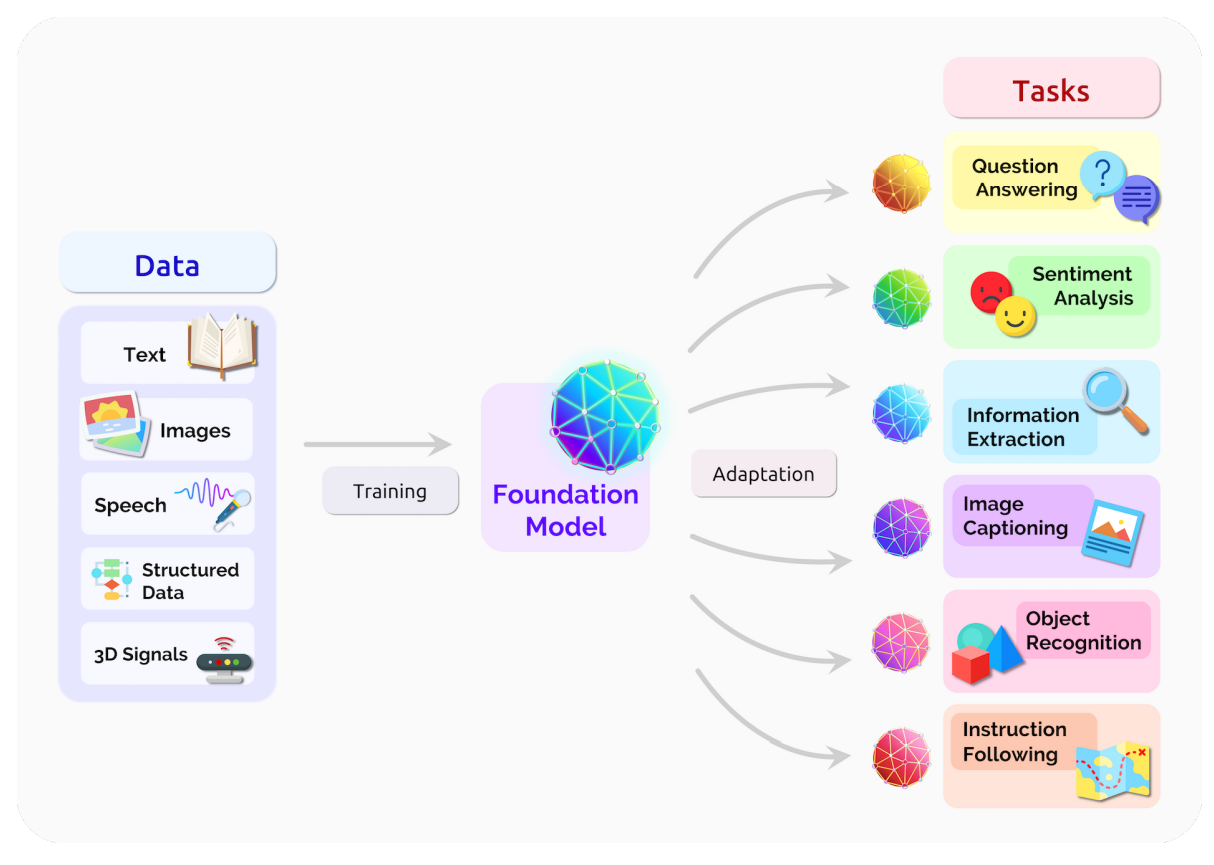
The Rise of The Foundation Model Paradigm
-
Foundation Model approach
- Pretrain models on pretext tasks, without supervision, on very large scale datasets.
- Adapt pretrained models to downstream tasks.
- Combine pretrained modules in more complex systems.
The Advantage of Scale of Data and Compute
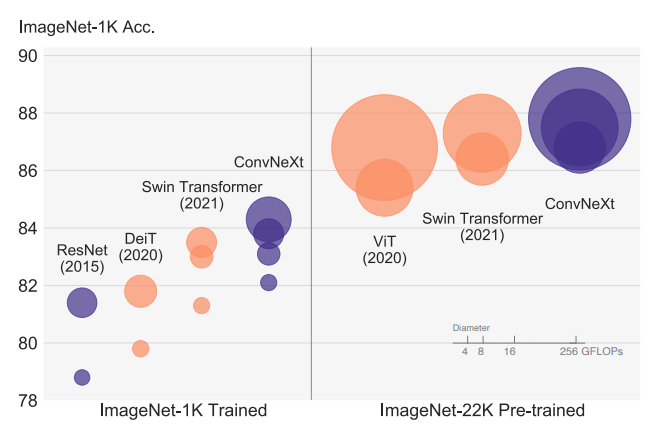
Linearly Accessible Information
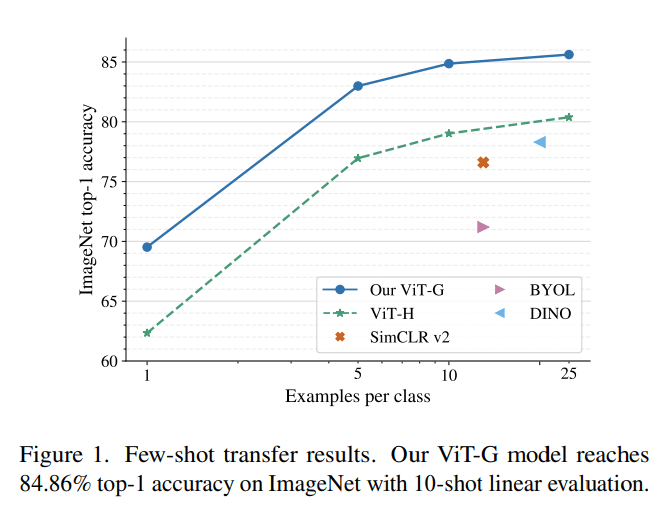
- Backbone of modern architectures embed input images as vectors in where d can typically be between 512 to 2048.
- Linear probing refers to training a single matrix to adapt this vector representation to the desired downstream task.
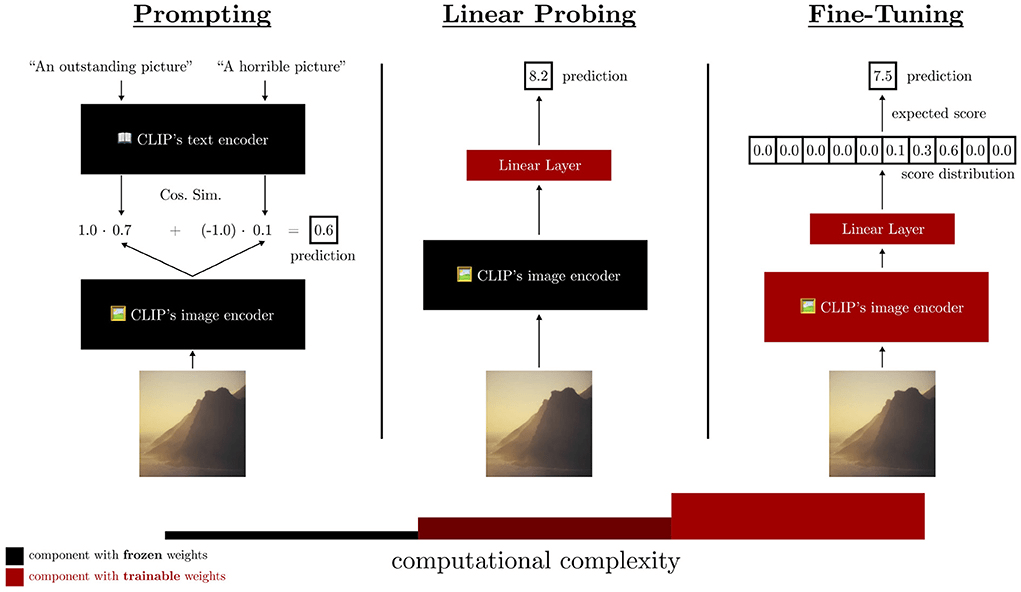
What This New Paradigm Could Mean for Us
-
Never have to retrain my own neural networks from scratch
- Existing pre-trained models would already be near optimal, no matter the task at hand
-
Saves a lot of time and energy
- Practical large scale Deep Learning even in very few example regime
- Searching for very rare objects in large surveys like Euclid or LSST becomes possible
-
Pretraining on data itself ensures that all sorts of image artifacts are already folded in the training.
- If the information is embedded in a space where it becomes linearly accessible, very simple analysis tools are enough for downstream analysis
- In the future, survey pipelines may add vector embedding of detected objects into catalogs, these would be enough for most tasks, without the need to go back to pixels

... but how does it work?
Masked Modeling
Sometimes, the simplest things just work...
An idea that comes from language models
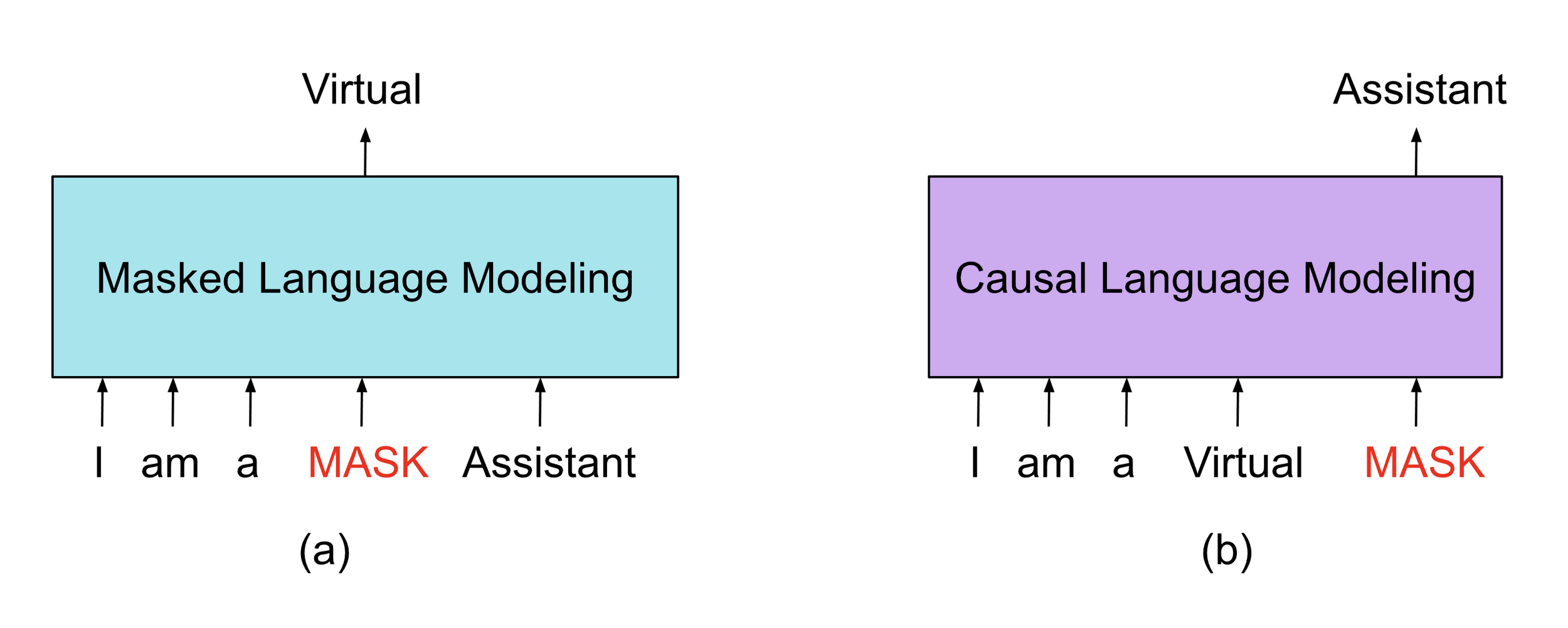
i.e. BERT (Devlin et al. 2018)
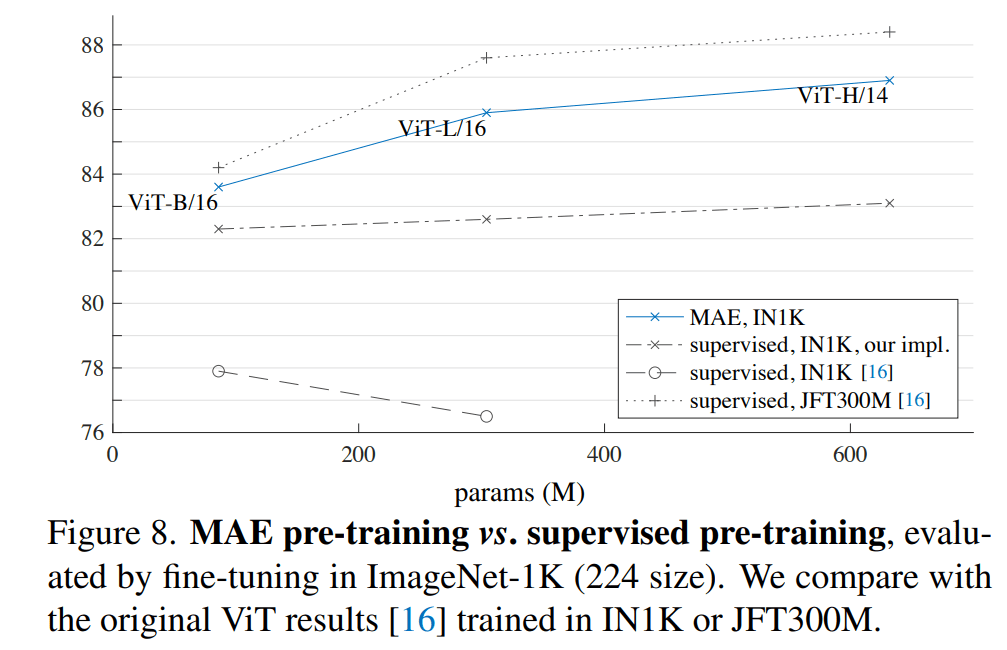
Masked Autoencoders Are Scalable Vision Learners (He et al. 2021)
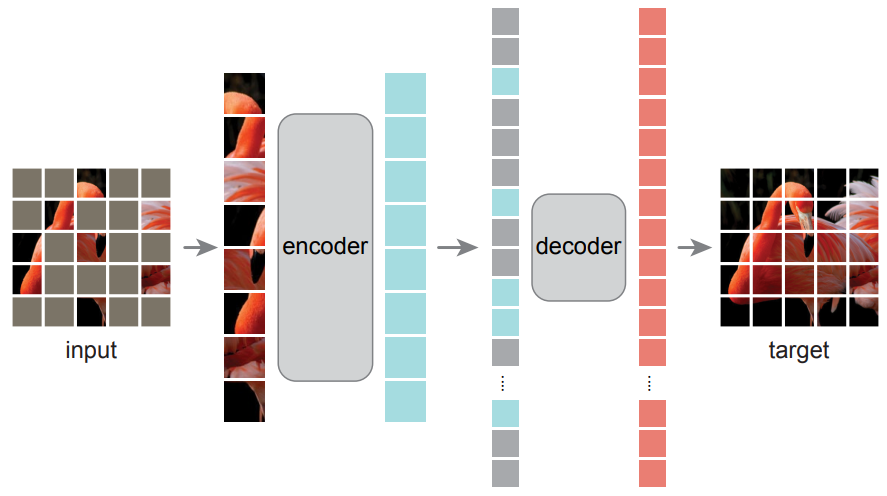

Masked Auto Encoding (MAE)
How to use such a model for classification
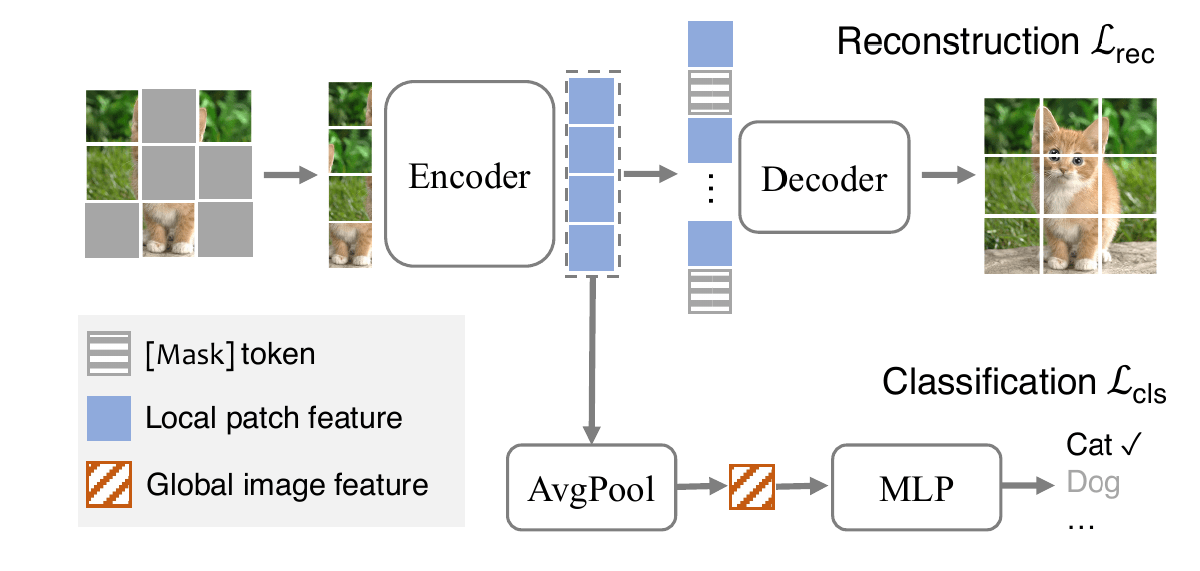
Credit: (Liang et al. 2022)
Application to Dense Prediction Tasks

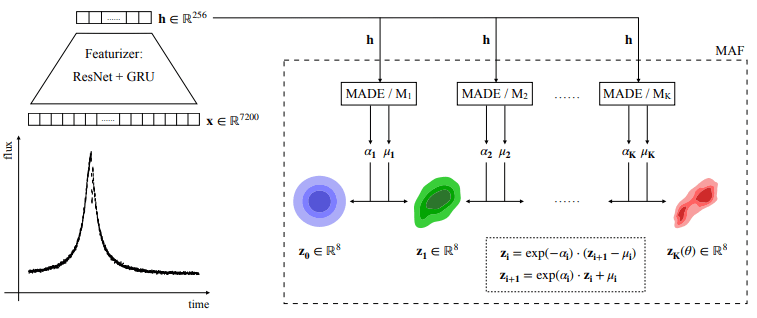
Example of Application on Astronomical Data: Specformer


- Pre-Training Galaxy Spectra Representation by Masked Modeling
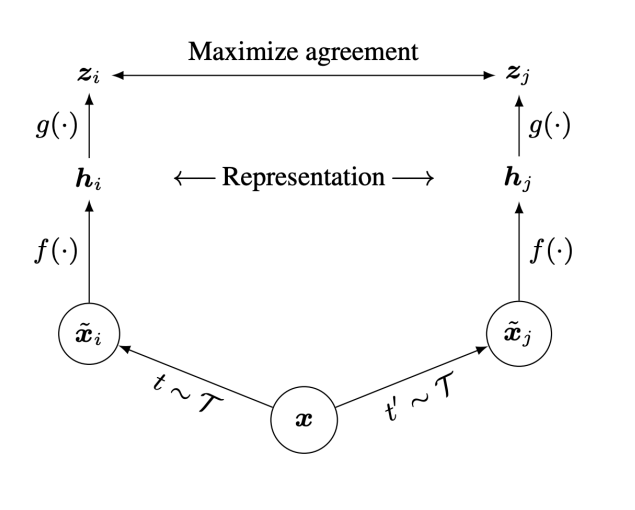
Multi-View Self-Supervised Contrastive Learning
MultiView Contrastive Learning e.g. SimCLR (Chen et al. 2000)

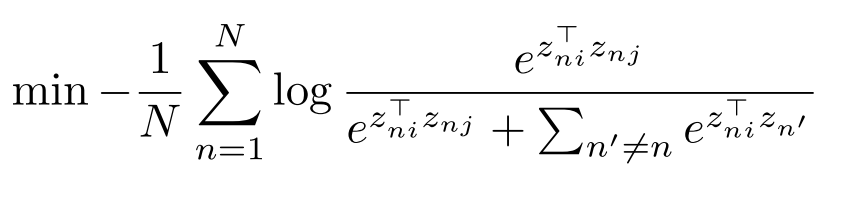
Contrastive Learning in Astrophysics

Self-Supervised similarity search for large scientific datasets (Stein et al. 2021)
Detecting Galaxy Tidal Features Using Self-Supervised Representation Learning

Project led by Alice Desmons, Francois Lanusse, Sarah Brough









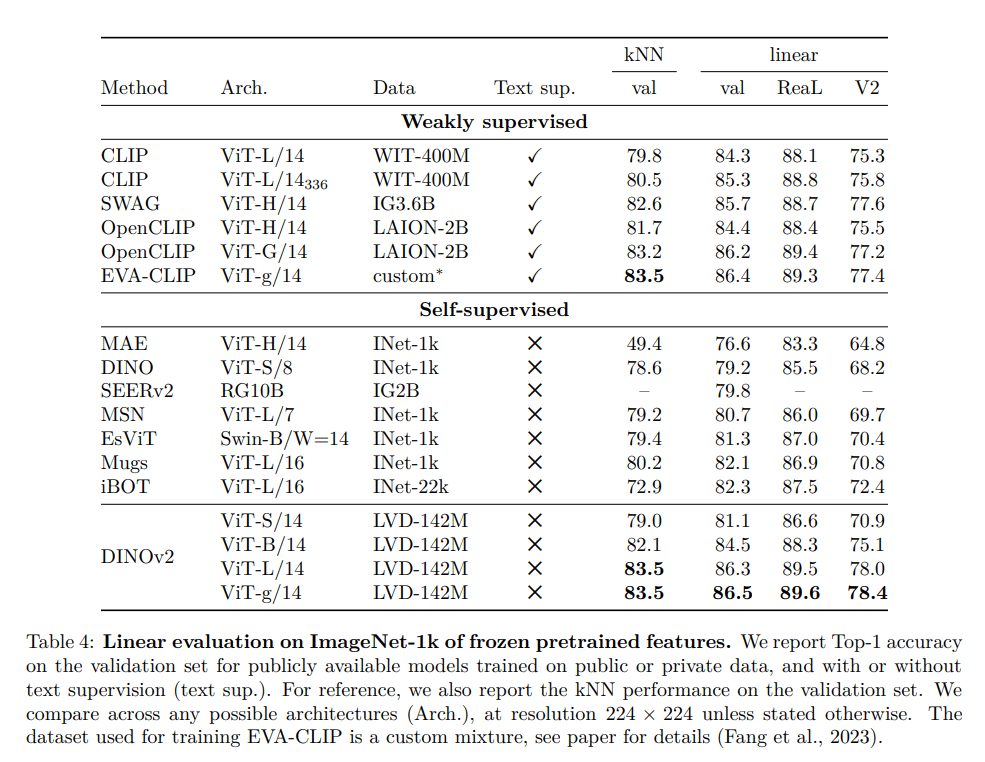
DiNOv2 (Oquab et al. 2023) A State of the Art Model (as of early 2024)


PCA of patch features
Dense Semantic Segmentation
Dense Depth Estimation
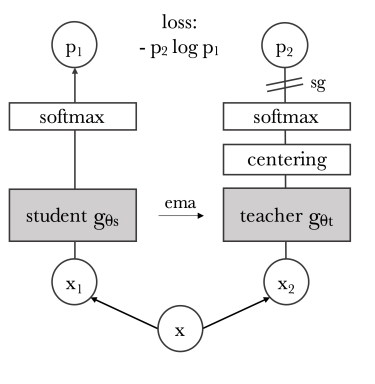
Weakly Supervised Contrastive Learning
Or what you can do when you do have independent views of an object...
Contrastive Language Image Pretraining
Contrastive Language Image Pretraining (CLIP)
(Radford et al. 2021)
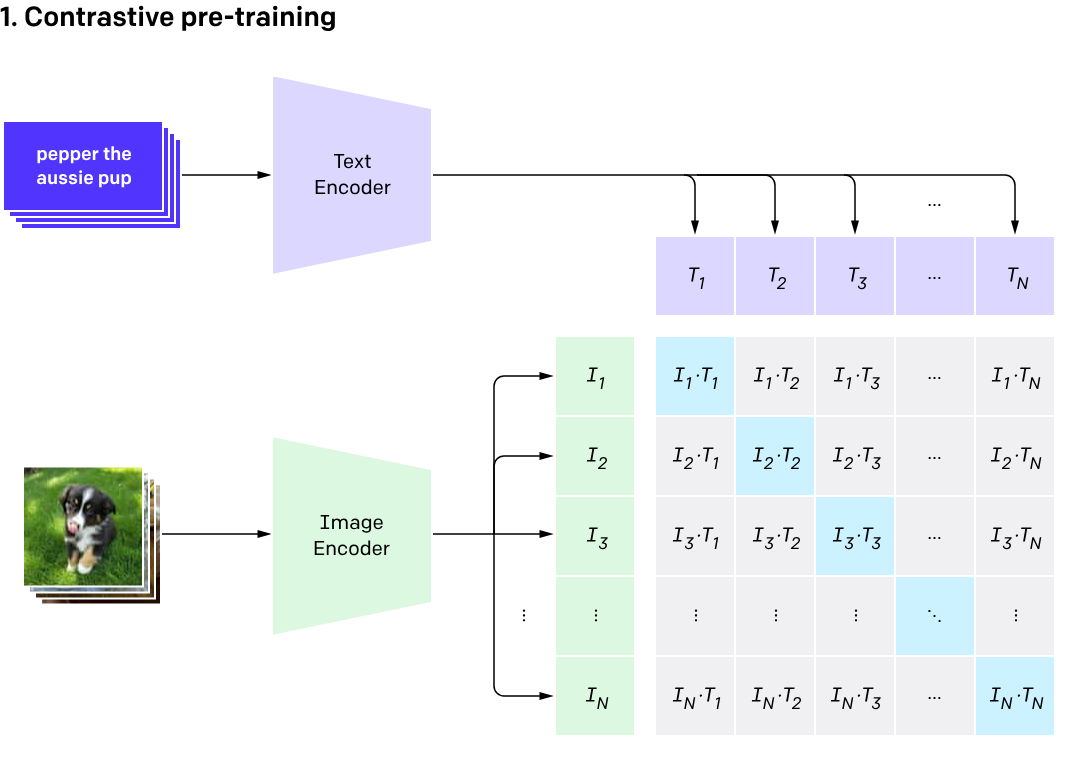
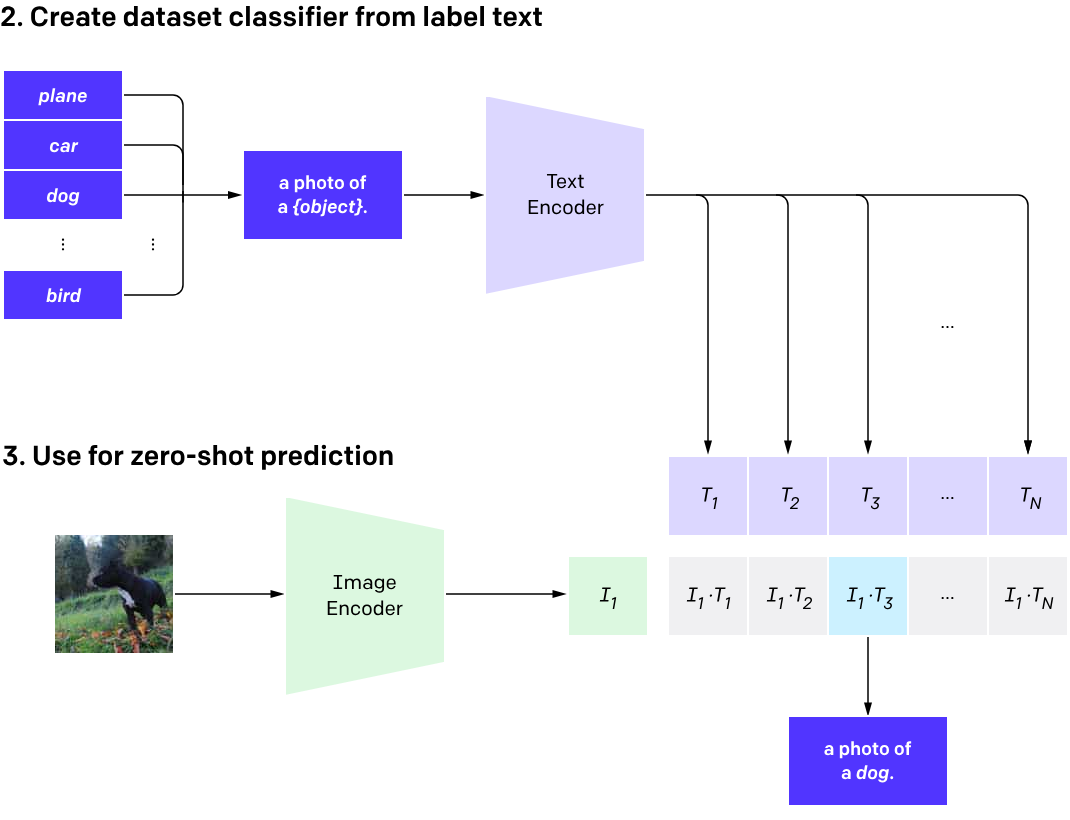
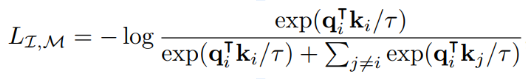
The Information Point of View
- The InfoNCE loss is a lower bound on the Mutual Information between modalities
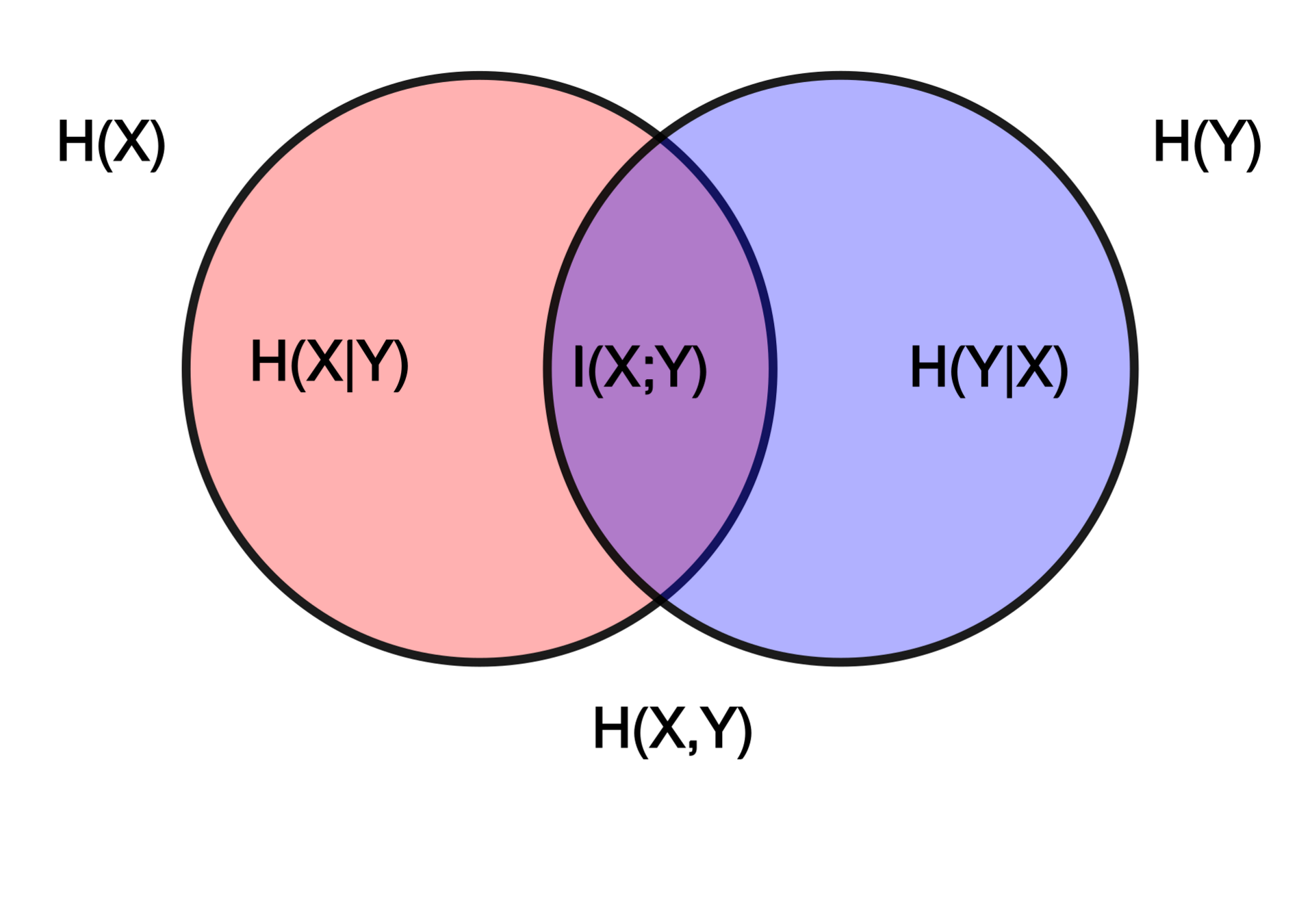
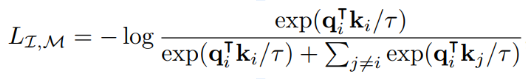
Shared information
One model, many downstream applications!
Flamingo: a Visual Language Model for Few-Shot Learning (Alayrac et al. 2022)


Hierarchical Text-Conditional Image Generation with CLIP Latents (Ramesh et al. 2022)
AstroCLIP
Cross-Modal Pre-Training for Astronomical Foundation Models

Project led by Francois Lanusse, Liam Parker, Siavash Golkar, Miles Cranmer
Accepted contribution at the NeurIPS 2023 AI4Science Workshop





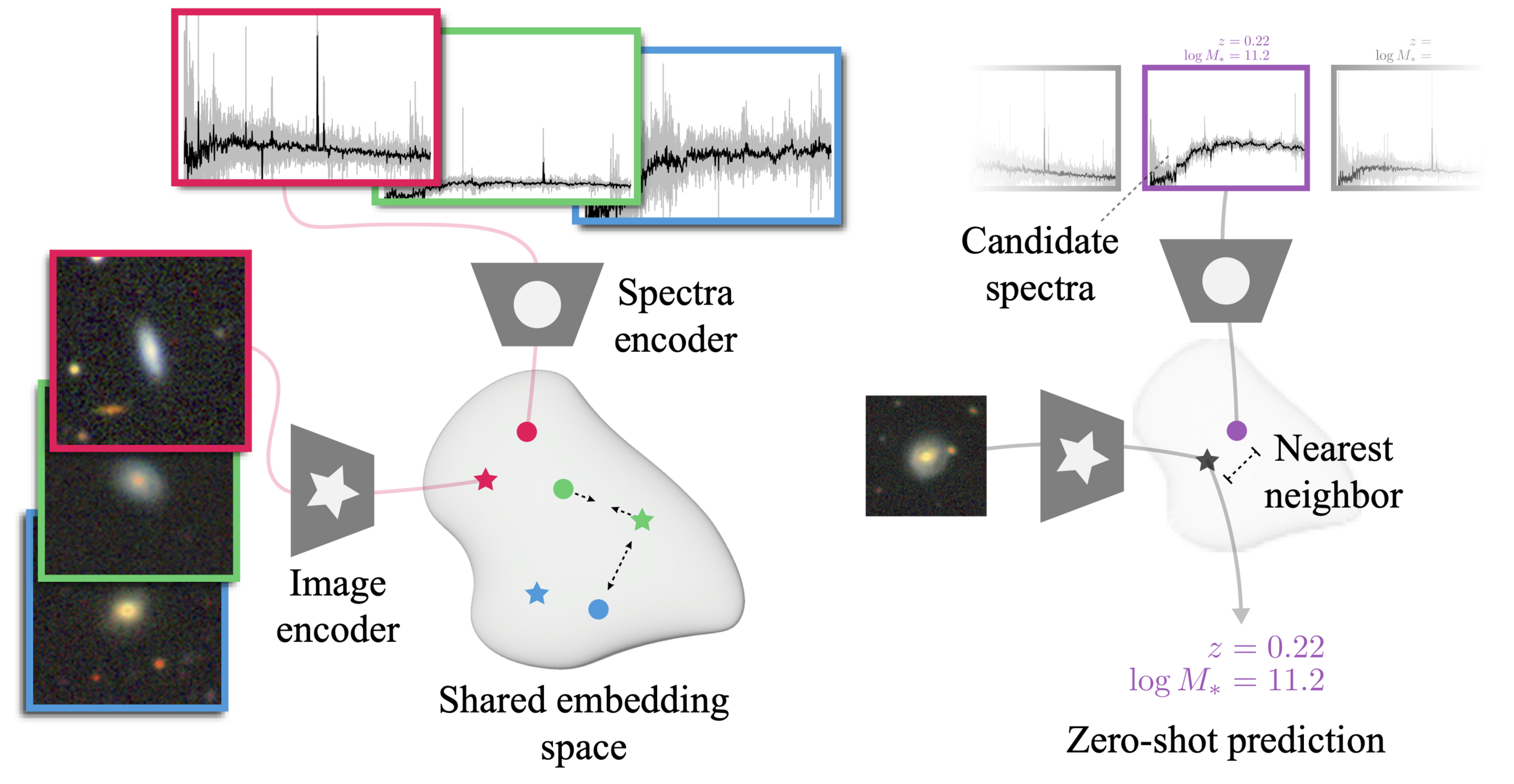
The AstroCLIP approach
- We use spectra and multi-band images as our two different views for the same underlying object.
- DESI Legacy Surveys (g,r,z) images, and DESI EDR galaxy spectra.
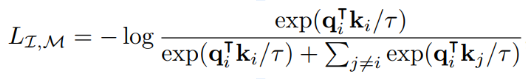


Cosine similarity search
The AstroCLIP Model (v2, Parker et al. in prep.)
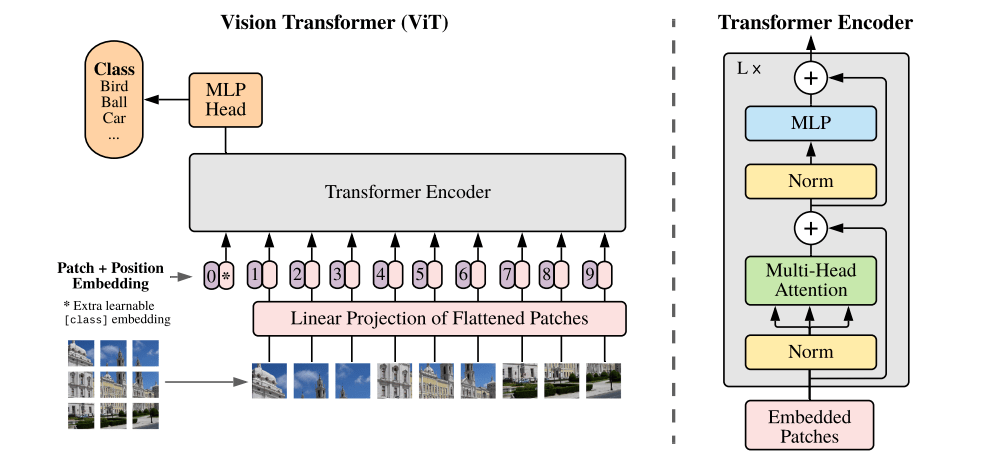
- For images, we use a ViT-L Transformer.
- For spectra, we use a decoder only Transformer working at the level of spectral patches.
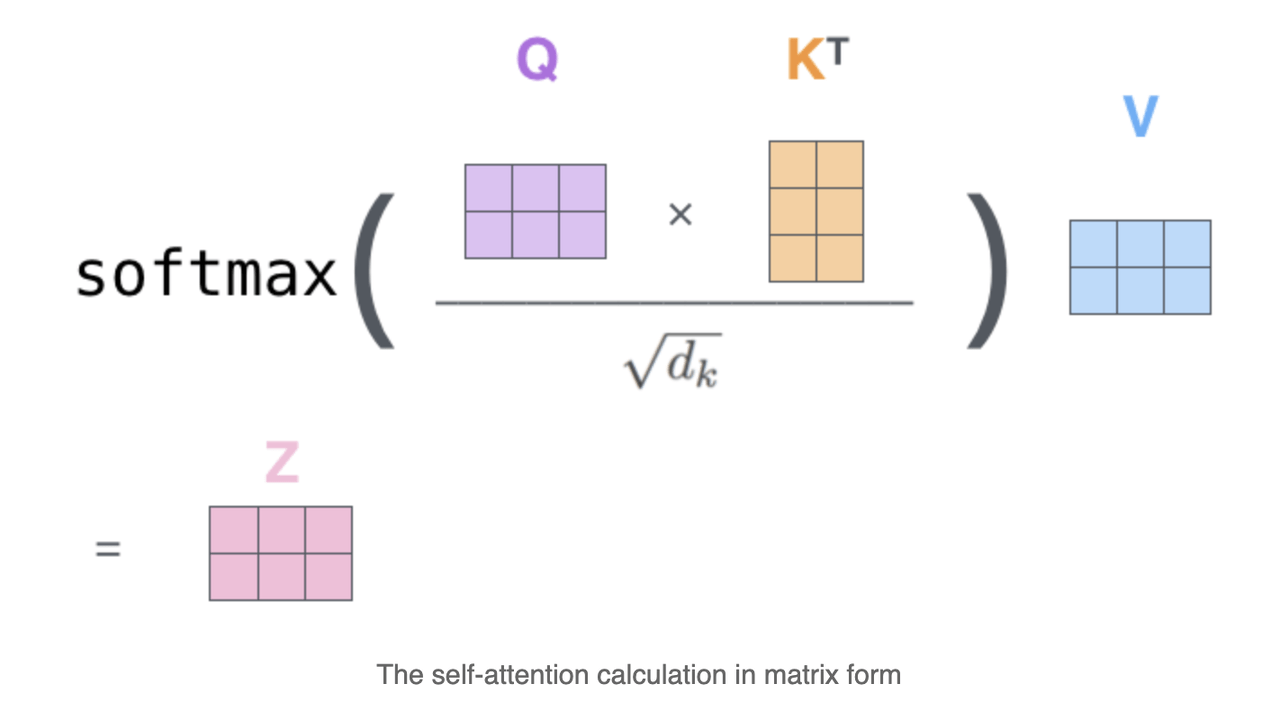
Evaluation of the model
- Cross-Modal similarity search


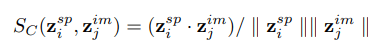


Image Similarity
Spectral Similarity

Image-Spectral Similarity
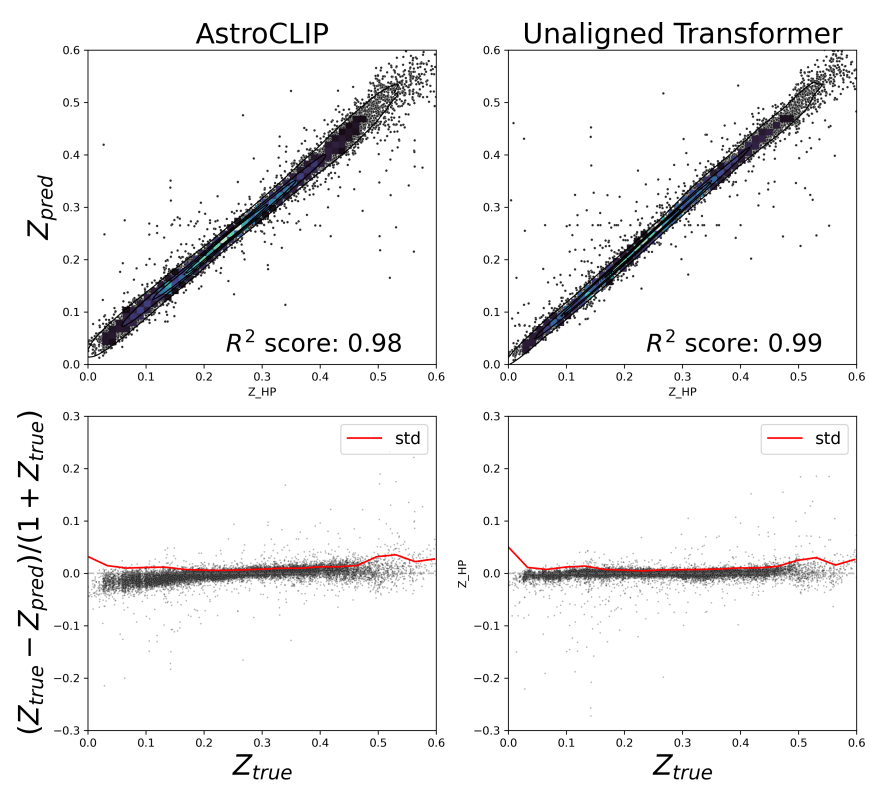
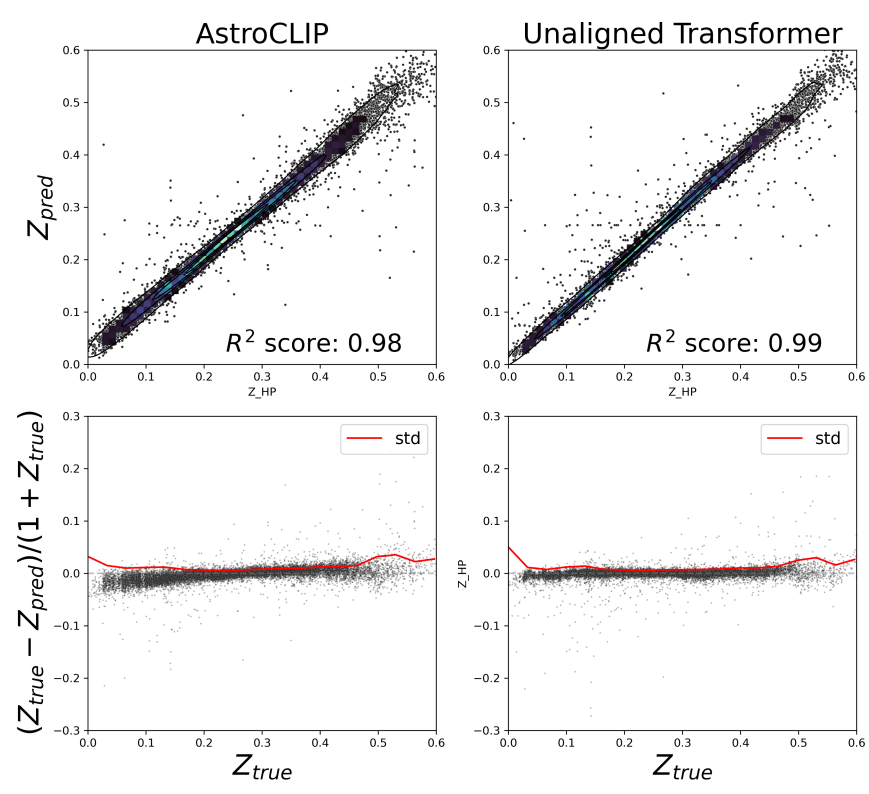
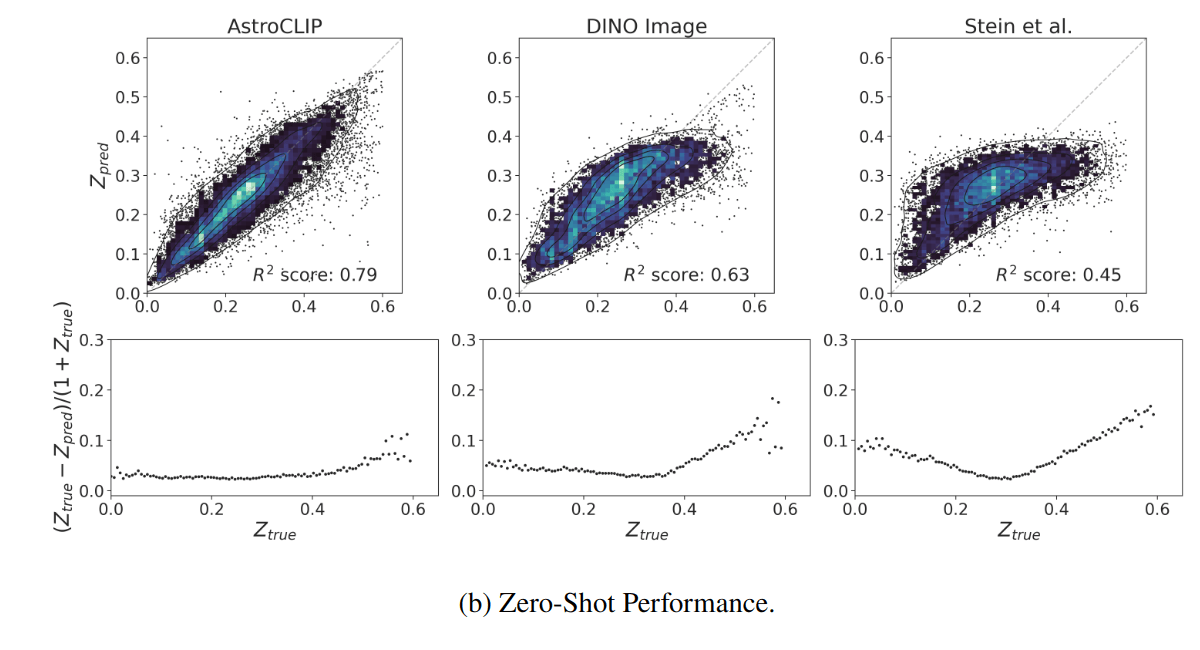
- Redshift Estimation From Images
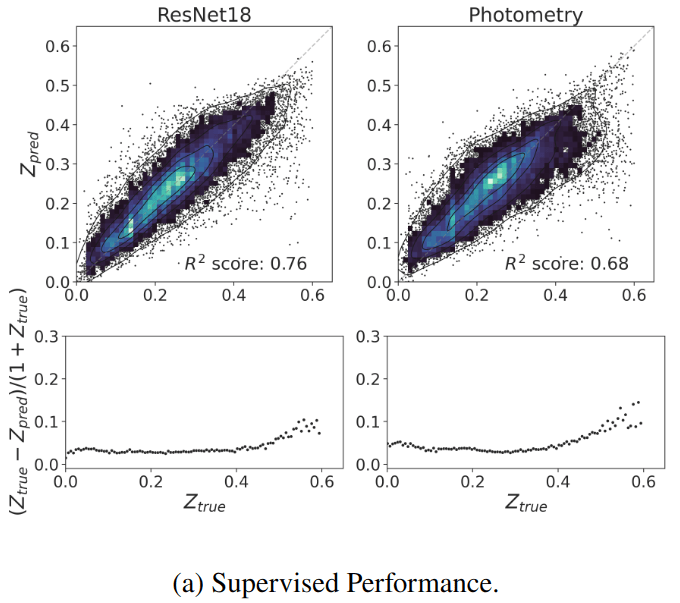
Supervised baseline
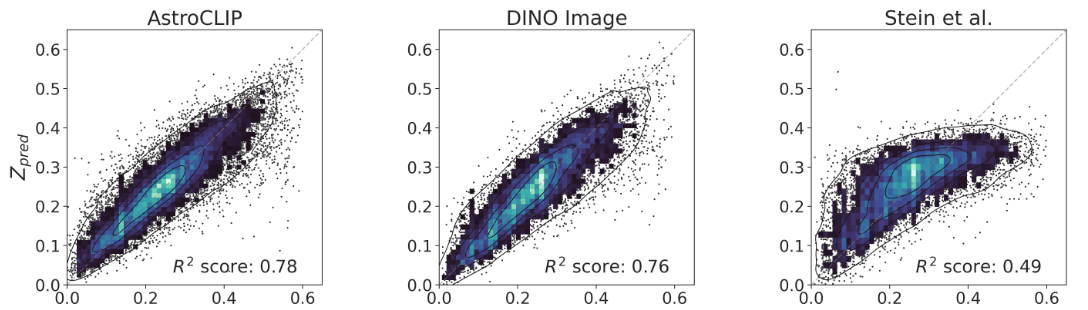
- Zero-shot prediction
- k-NN regression
- Few-shot prediction
- MLP head trained on top of frozen backbone
- Galaxy Physical Property Estimation from Images and Spectra
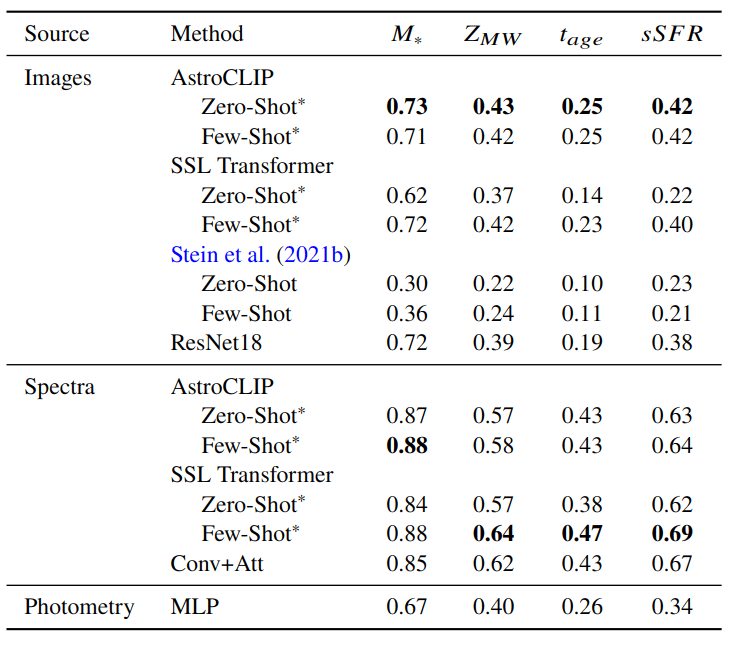
We use estimates of galaxy properties from the PROVABGS catalog (Hahn et al. 2023) (Bayesian spectral energy distribution (SED) modeling of DESI spectroscopy and photometry method)
of regression

Negative Log Likelihood of Neural Posterior Inference
- Galaxy Morphology Classification
Classification Accuracy
We test a galaxy morphology classification task using as labels the GZ-5 dataset (Walmsley et al. 2021)


Intro to Self Supervised Representation Learning for Astrophysics
By eiffl
Intro to Self Supervised Representation Learning for Astrophysics
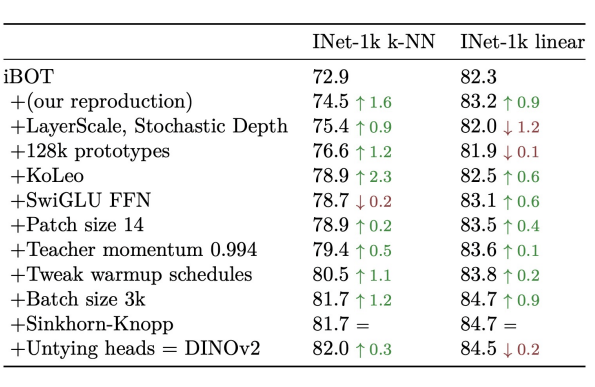
- 707



