The DESC Tomography Challenge
Francois Lanusse, @EiffL
On behalf of the DESC tomo challenge team (Joe Zuntz, Anze Slosar, Alex Malz)
Gravitational Lensing
What is a "3x2pt" analysis?
- The "3" means three cosmological probes
- The "x2pt" means two-point correlations (auto- and cross-)
\delta_m
Three different ways to probe the matter distribution by computing correlation functions of the observables.
Where does tomography come in?
The response of these probes depends on the redshift of the galaxies we are looking at
Why bother binning?
Binning: The art of splitting galaxies into sub-samples to capture as much information as possible about the redshift-dependence of the matter distribution
2 bins
4 bins
Ok, great, so why are we even discussing it?
Estimating redshift is hard!
The problem with Photo-z
We do not have access to the real redshift of galaxies, so we try to estimate it based on multi-band photometry, i.e. photometric redshifts (photo-z)
Credit: Graham et al. arxiv:2004.07885
Why binning isn't trivial
Let's imagine a strategy where we first try to estimate photoz, and bin on these photoz
| total 3x2pt SNR | perfect bins | photoz bins |
|---|---|---|
| 2 bins | 916 | 896 |
Why it's even more complicated in DESC
- In LSST DESC, for the purpose of measuring the lensing signal with the metacalibration method, we need to define bins only using the few bands used for shape measurement.
- This means in practice, that we only have access to the photometry in (g)riz bands to define the bins
- Once the bins are defined, the actual n(z) for each bin can used all available bands/information
The
Challenge
The DESC Idealized Tomo Challenge
- What we give you:
- only 3 or 4 bands photometry (riz, griz)
- True redshift for each galaxy
-> This data comes from the DC2 Simulation made by DESC (see Korytov et al. )
- Your mission, should you choose to accept it:
- Timeline:
- Half-time leaderboard at the end of July
- Challenge closes at the end of August
Find the best possible way to split the galaxy sample in bins based on photometry, so that you maximize the cosmological information from a 3x2pt analysis
Metrics
- Total Signal-to-Noise
- Figure of Merit
- We are still open to other metrics! We will not judge the winning method strictly based on the numerical value of these two metrics.
m_{SNR} = \sqrt{\mu^t \mathbf{C}^{-1} \mu}
m_{FOM} = \frac{1}{\sqrt{\det(\mathbf{F}^{-1})_{\Omega_m \sigma_8}}} \quad where \quad \mathbf{F} = \frac{\partial \mu}{\partial \theta}^t \mathbf{C}^{-1} \frac{\partial \mu}{\partial \theta}
An example: Photometric Binning by
Random Forest
We propose a simple example as a baseline, feel free to take inspiration from it, but feel free to explore completely different ideas!
-
Step I: Define desired bins in true redshifts
=> For this, we simply split the true redshift distribution in bins of equal numbers of galaxies.
- Step II: Train a classifier to assign the bin value to a galaxy based on photometry
- Step III: Profit!
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier()
classifier.fit(training_photometry_data, training_bin)
| Results for 2 bins | SNR 3x2 | FOM 3x2 |
|---|---|---|
| With true redshifts | 915 | 24216 |
| With photometric classifier | 896 | 2548 |
=> It's working but we see a degradation in score, because bins are now overlaping
Get started rightaway on this example on Google Collaboratory
What is not perfect in this solution?
- At the lowest level, of course you might propose a better classifier than this stock Scikit-Learn Random Forest.
- Why did we choose to define bin boundaries in terms of true redshift?
- maybe we should define these boundaries in way that acknowledges the photometric degeneracies....
- maybe we should define these boundaries in way that acknowledges the photometric degeneracies....
- Think outside the box :-) At the end of the day, we don't care about photoz, we only care about our hability to constrain cosmology!
How to enter the challenge?
- Your first stop is the challenge github repo:
There you will find:- README, with instructions and FAQ
- Issues, where you can ask any question you want about the challenge
- Pull Requests, where you can see solutions entered in the challenge
- To install requirements:
- To download the data:
- To apply the baseline classifier method:
-> The results can be found in the examples/ folder and will look like this:
$ conda install -c conda-forge pyccl cosmosis-standalone camb firecrown
$ pip install sacc click progressbar scikit-learn$ python -m tomo_challenge.data$ python bin/challenge.py example/example.yaml$ more example/example_output.txt
RandomForest run_1 {'bins': 1} {'SNR_ww': 134.80948870306673, 'SNR_gg': 555.4535070472674, 'SNR_3x2': 562.3045275125236, 'FOM_3x2': 11406.381379130828}
RandomForest run_2 {'bins': 2} {'SNR_ww': 153.37996427859213, 'SNR_gg': 749.4259413373646, 'SNR_3x2': 752.8800006487635, 'FOM_3x2': 11420.79691061082}
RandomForest run_3 {'bins': 3} {'SNR_ww': 159.18538698343457, 'SNR_gg': 922.7346985760454, 'SNR_3x2': 925.4853956272517, 'FOM_3x2': 43768.68018337518} Implementing a new classifier
- Simply follow the example in tomo_challenge/classifiers/random_forest.py
- Add a configuration file for your method in tomo_challenge/example/ following the example in example.yaml
- Run the training/testing using the challenge engine:
from .base import Tomographer
class MyTomographer(Tomographer):
""" My awesome Tomographic method """
def __init__ (self, bands, options):
# ....
def train (self, training_data, training_z):
# Some magic happens here to train/fit the model
def apply (self, data):
# Attribute a bin to each galaxy
return tomo_bin(data)$ python bin/challenge.py example/my_tomographer.yamlSubmitting your solution
- Open a fork of the main challenge repo
- Add your code
- Open a Pull Request, documenting your method and your findings
- Here is an example
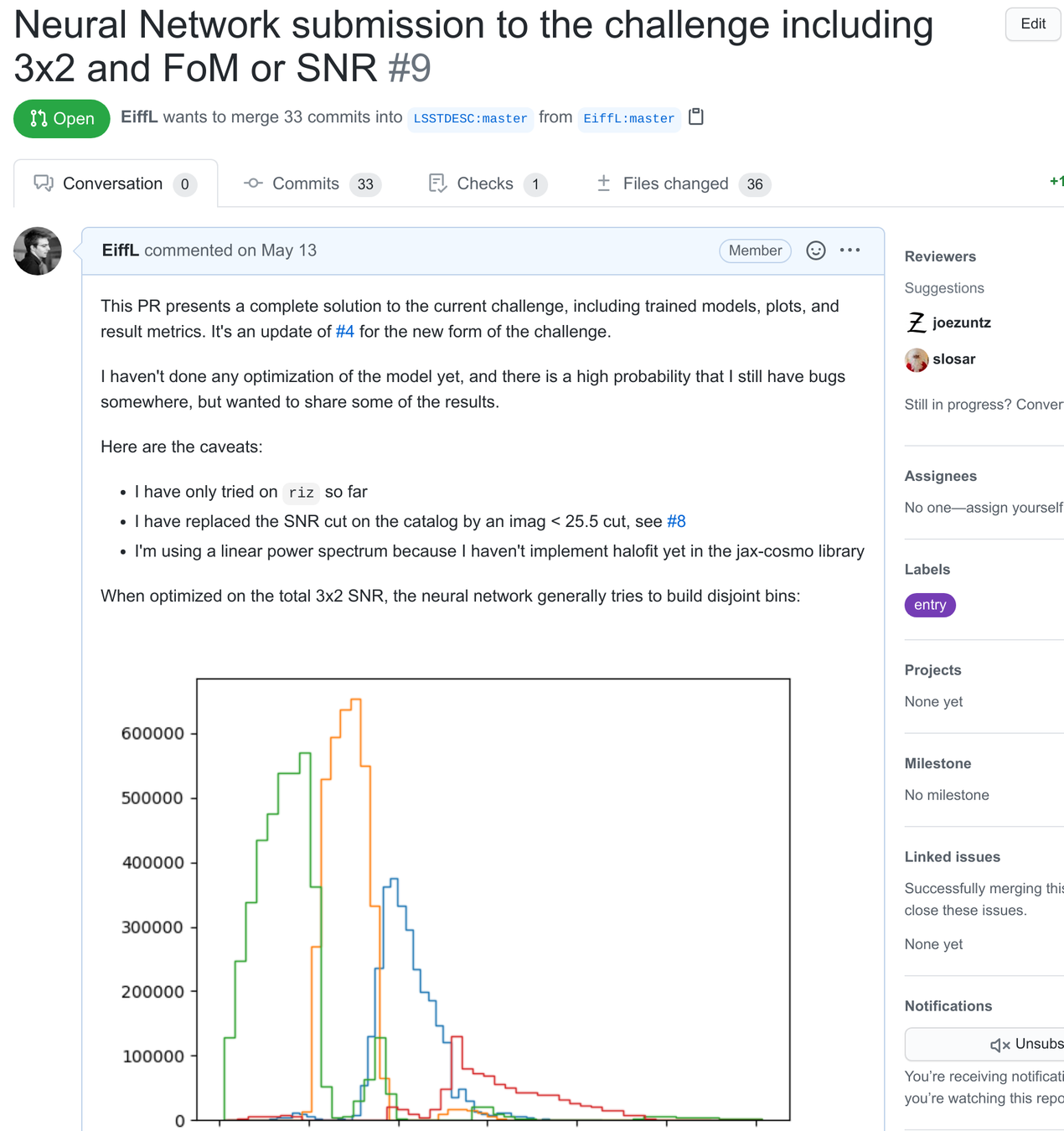
Conclusion
- The mission: Challenge the status-quo on tomographic 3x2pt, find a new way to define tomographic bins.
- Remember this is an idealized challenge, we are glossing over a lot of other issues.
- Challenge closes at the end of August, half-time leaderboard end of July
- For any questions/comments, don't hesitate to:
- Open an issue on the GitHub Repository
- Get in touch with us on the LSSTC Slack, in the #desc-3x2pt channel
- Thank you!
The DESC Tomo Challenge
By eiffl
The DESC Tomo Challenge
An introduction to the challenge
