Universidad Nacional Autónoma de México
Introducción a la Física Computacional
Implementación del Perfectly Matched Layer (PML) al código de FDTD
Autor: Lic. Favio Vázquez
Supervisor: Dr. Yevgeniy Kolokoltsev
14 de noviembre de 2016
Introducción teórica al
PML
Introducción teórica al PML
¿Qué es un PML?
En algunas situaciones necesitamos modelar un problema electrodinámico en el cual, entre comillas, no existan fronteras, es decir, un problema de fronteras abiertas.
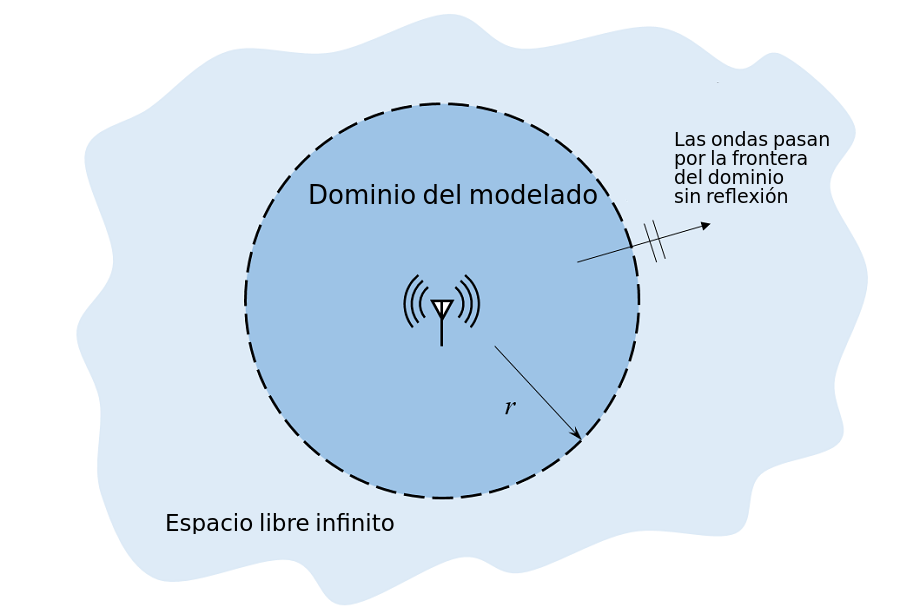
Para hacer esto comúnmente se utilizan técnicas y métodos que absorven las ondas en los bordes de una simulación FDTD.
Introducción teórica al PML
¿Qué es un PML?
El modo en que el PML resuelve este problema es introduciendo una capa de grosor finito a las fronteras del dominio de simulación, la cual absorve ondas a través de conductividades eléctricas y magnéticas, no físicas, causando un decaimiento exponencial de la amplitud del campo.
Las reflexiones adentro del espacio de simulación con PML se eliminan apareando perfectamente las impedancias de los dos medios, y calculando con cuidado las conductividades de PML.
Introducción teórica al PML
El primer modo efectivo de aplicar un PML fue introducido por J. P. Bérenger en 1994; el cual consistía en la reflexión y refracción de ondas planas en la interfaz entre un medio dieléctrico sin pérdidas y otro con pérdidas.
Para eso es necesario separar la onda plana en dos modos ortogonales, y encontrar la condición para la no reflexión, y luego lo único que queda es separar estas ecuaciones dentro de las ecuaciones de Maxwell.
H_z
Esta posibilidad fue encontrada por Bérenger en este artículo, y está sujeta a la introducción de dos conductancias independientes para el mismo vector de campo magnético, lo cual no es físico, ya que solo tiene una dirección, pero es un artificio numérico
Introducción teórica al PML
Ecuaciones relevantes (modo TM):
\epsilon_2 \frac{\partial E_x}{\partial t} + \sigma_y E_x = \frac{\partial H_z}{\partial y}
\epsilon_2 \frac{\partial E_y}{\partial t} + \sigma_x E_y = - \frac{\partial H_z}{\partial x}
\mu_2 \frac{\partial H_{z}}{\partial t} + \sigma_{m} H_{z} = \frac{\partial E_y}{\partial x} - \frac{\partial E_y}{\partial x}
Caso isotrópico
Caso anisotrópico
H_z = H_{zx} + H_{zy}
\epsilon_2 \frac{\partial E_x}{\partial t} + \sigma_y E_x = \frac{\partial H_z}{\partial y}
\epsilon_2 \frac{\partial E_y}{\partial t} + \sigma_x E_y = - \frac{\partial H_z}{\partial x}
\mu_2 \frac{\partial H_{zx}}{\partial t} + \sigma_{m,x} H_{zx} = - \frac{\partial E_y}{\partial x}
\mu_2 \frac{\partial H_{zy}}{\partial t} + \sigma_{m,y} H_{zy} = \frac{\partial E_x}{\partial y}
Introducción teórica al PML
Ecuaciones relevantes (modo TM):
H_z = H_{zx} + H_{zy}
\frac{\sigma_x}{\epsilon_1} = \frac{\sigma_{m,x}}{\mu_1}
H_z = H_0 (e^{-jk_{1_x}x+k_{1_y}y})(e^{\sigma_x x \eta_1 \cos{\theta_i}})
E_x = - H_0 \eta_1 \sin{\theta_i} (e^{-jk_{1_x}x+k_{1_y}y})(e^{\sigma_x x \eta_1 \cos{\theta_i}})
E_y = H_0 \eta_1 \cos{\theta_i} (e^{-jk_{1_x}x+k_{1_y}y})(e^{\sigma_x x \eta_1 \cos{\theta_i}})
Término de atenuación
\epsilon_2 \frac{\partial E_x}{\partial t} + \sigma_y E_x = \frac{\partial H_z}{\partial y}
\epsilon_2 \frac{\partial E_y}{\partial t} + \sigma_x E_y = - \frac{\partial H_z}{\partial x}
\mu_2 \frac{\partial H_{zx}}{\partial t} + \sigma_{m,x} H_{zx} = - \frac{\partial E_y}{\partial x}
\mu_2 \frac{\partial H_{zy}}{\partial t} + \sigma_{m,y} H_{zy} = \frac{\partial E_x}{\partial y}
Implementación
Implementación
Se creó una clase que hereda las funciones y estructuras de EMField pero que agrega las variables necesarias para dividir el campo. Para hacer esto se modificaron los archivos:
- emfield.h
- emfield.cpp
Utilizando DF se modificaron las ecuaciones de campo, para así implementar las ecuaciones mostradas.
- optics.h
- optics.cpp
Se creó la caja de cómputo, haciendo la geometría de la frontera en la cual se implementaría el PML.
- visual_field.cpp
Se modificó la forma en la cual se calcula la energía de los campos para que se tomara en cuenta la división del campo magnético.
Implementación
void EMFieldPML::eval_cell_E(int i, int j){
TECell& cij = field[i][j];
TECell& cij1 = c(i,j-1);
TECell& ci1j = c(i-1,j);
double Hij = cij.Hzx + cij.Hzy;
double Hij1 = cij1.Hzx + cij1.Hzy;
double Hi1j = ci1j.Hzx + ci1j.Hzy;
cij.Ex += (dt/dl*(1/epsilon))*( (Hij/cij.epsilon_mult -
Hij1/cij1.epsilon_mult) ) - cij.Ex*cij.sigmax*dt/(cij.epsilon_mult*epsilon);
cij.Ey += (dt/dl*(-1/epsilon))*( (Hij/cij.epsilon_mult -
Hi1j/ci1j.epsilon_mult) - cij.Ex*cij.sigmay*dt/cij.epsilon_mult*epsilon);
}void EMFieldPML::eval_cell_H(int i, int j){
TECell& cij = field[i][j];
TECell& cij1 = c(i,j+1);
TECell& ci1j = c(i+1,j);
cij.Hzx += (dt/dl*(1/mu))*( - (ci1j.Ey/ci1j.mu_mult -
cij.Ey/cij.mu_mult) - cij.Hzx*cij.sigmam_x*dt/cij.mu_mult*mu);
cij.Hzy += (dt/dl*(1/mu))*( (cij1.Ex/cij1.mu_mult -
cij.Ex/cij.mu_mult) - cij.Hzy*cij.sigmam_y*dt/cij.mu_mult*mu);
}Demo
Comentario: Matemáticamente hablando, el PML es simplemente un dominio que tiene una permitividad y permeabilidad anisotrópica y compleja. Aunque los PMLs son teóricamente no reflejantes, sí exhiben alguna reflexión debido a la discretización numérica: la malla. Para minimizar esta reflexión, se debe utilizar una malla en el PML que se ajuste (lo más perfecto posible) a las anisotropías en las propiedades del material.
PML
By Favio Vazquez
