Gradient Boosting

one tree at a time

Ferran Muiños @fmuinos

BBG-SBNB seminar (IRB Barcelona)

Thursday 20180712

Aim of the talk

"Demystify tree ensemble methods"

  • Quick overview of regression

  • Gentle intro to decision trees and tree ensembles

  • What does gradient boosting intend?

  • Practical usage

  • Some examples along the way

Regression

X \stackrel{\textrm{dependence}}{\longrightarrow} Y

covariates

response

Regression

X \stackrel{\textrm{dependence}}{\longrightarrow} Y

covariates

response

Problem statement:

Find a function     that gives a precise description of the dependence relationship between     and     :

 

 

f
X
Y
Y = f(X) + \varepsilon

Regression

Alternative problem statement:

Given a collection of samples

 

 

 

find a function     that provides:

  • Low-error approximations                       (good fit)
  • Expected good fit for any dataset of the same kind.
s_1 = \{x_1, y_1\}
\vdots
s_K = \{x_K, y_K\}
f
f(x_i) \sim y_i
X \stackrel{\textrm{dependence}}{\longrightarrow} Y

covariates

response

First example: cell culture

x
y

First example: cell culture

x
y

What patterns do we see?

First example: cell culture

x
y

Perfect fit!

But do not expect it to fit new data :(

First example: cell culture

f(x) = \frac{1}{k}\sum_{i \in \mathcal{N_k(x)}} y_i

Average Smoothing

f(x) = \frac{\sum_{i=1}^N K(x - x_i)y_i}{\sum_{i=1}^N K(x - x_i)}

Nadaraya-Watson

K(x)

: bell-shaped kernel

First example: cell culture

Linear

f(x) = ax + b
f(x) = ax^2 + bx + c

Quadratic

First example: cell culture

Parametric methods:

  • assume global shape 
  • very restricted overall
  • maybe inaccurate prediction
  • maybe easier to interpret

Smoothers:

  • agnostic shape 
  • shape is locally restricted       
  • useful for prediction
  • more difficult to interpret
f(x) = E(Y | X = x)

Whatever the strategy, we want some

f:\mathbb{R}^n \to \mathbb{R}

that satisfies

f(x) = E(Y | X = x)

Whatever the strategy, we want some

f:\mathbb{R}^n \to \mathbb{R}

that satisfies

Applicable to datasets with n covatiates

f(x) = E(Y | X = x)

Whatever the strategy, we want some

f:\mathbb{R}^n \to \mathbb{R}

that satisfies

This is the key!

How do we know what to expect after all?

Data subsets

Dataset

Training dataset

Test dataset

Fit the model

Test the model

Bagging

Bagging = Bootstrap + Aggregating

  • Pick several random subsets of samples:
  • Train a model with each subset:
  • Create a consensus model:
f_1, \ldots, f_K
\mathcal{S}_1, \ldots, \mathcal{S}_K
f = \mathcal{C}(f_1, \ldots, f_K)

"Averaging" is the typical way to reach consensus                                           

f(x) = \frac{1}{K}\sum_{i=1}^K{f_i(x)}

Bagging does a decent work even with weak models...

I am a small tree.

Learn weak, die hard.

Tree Ensembles

Trees (a.k.a. decision trees) are functions of a particular kind:

  • Have a root where the input goes         
  • Leaves are values
  • Inner nodes are if-else statements
  • If-else conditions are of the form
x_1 \leq 7
x_2 \leq 9
x = (x_1, \ldots, x_n)
1
2
4
x_i \leq a

Example

x \leq 15

yes

no

x \leq 10
15
7

yes

no

10

1st split

2nd split

What is the best least-squares fitting tree?

?

  • Root splits the data: 
  • Set leaf values:
S_1 \cup S_2
\mu_1 = \textrm{mean}\{y_j\;|\; j\in S_1\}
\mu_2 = \textrm{mean}\{y_j\;|\; j\in S_2\}

?

For which split do we get minimum RSS?

What is the best least-squares fitting tree?

?

  • Root splits the data: 
  • Set leaf values:
S_1 \cup S_2
\mu_1 = \textrm{mean}\{y_j\;|\; j\in S_1\}
\mu_2 = \textrm{mean}\{y_j\;|\; j\in S_2\}

YES!

For which split do we get minimum RSS?

Bagging with stumps...

Random Forests

from sklearn.ensemble import RandomForestRegressor

model = RandomForestRegressor(n_estimators=3, max_depth=1)
res = model.fit(temp, rate)

Random Forests

n_estimators=1000, 
max_depth=1
n_estimators=1000, 
max_depth=2

Gradient Boosting

Greedy cousin of the Random Forest:

  • Model = sum of trees
  • Trees are computed sequentially
+
+ \;\ldots

How it works

Fix a loss function:                 e.g.  

Initialize the model with an educated guess:

At each step      we find a new tree      :

 

 

The tree      is such that the following "loss" is small:

T_0

Training Samples:

s_1 = \{x_1, y_1\}
\vdots
s_K = \{x_K, y_K\}
L(y, \hat{y})
t_m
T \leftarrow T_{m-1} + \nu \cdot t_m
\frac{1}{2}\sum_{i=1}(y_i - \hat{y}_i)^2
t_m
\textrm{Loss}_m (\textbf{x}) = \sum_{i=1}^K L(y_i, T_{m-1}(x_i) + t_m(x_i)) + \Omega(t_m)
m

How it works

Using Taylor's expansion this can be re-written:

 

 

The tree      is such that the following objective is minimized:

t_m
\textrm{Obj}_m = \sum_{i=1}^K L(y_i, T_{m-1}(x_i)) + g_it_m(x_i) + h_it_m(x_i)^2 + \Omega(t_m)
\sum_{i=1}^K g_it_m(x_i) + h_it_m(x_i)^2 + \Omega(t_m)

How it works

 

The tree      is such that the following objective is minimized:

t_m
\sum_{i=1}^K g_it_m(x_i) + h_it_m(x_i)^2 + \Omega(t_m)

These pseudo-residuals are computed using the first derivative of the loss function L

These factors are computed using the second-derivative of the loss function L 

Regularization term

Tunning hyperparams

  • loss function
  • learning rate a.k.a. shrinkage:
  • number of estimators (trees)
  • maximum depth of trees
  • randomization rules:
    • subset of samples (size)
    • per-tree/per-split subset of covariates (ratio)
  • regularization parameters

We can introduce rules to constraint the search for each update. These rules define the "learning style" of the model.

T \leftarrow T_{m-1} + \nu \cdot t_m
\nu

Why Tree Ensembles?

Upsides:

  • Non-parametric (shape agnostic)               
  • Up to a variety of regression and classification tasks 
  • Modelling flexibility
  • Admit a large number of covariates
  • Good prediction accuracy
  • Good at capturing interactions between covariates by design
  • Interpretation is feasible: ranking variables, partial dependence
  • Efficient functions

Downsides:

  • Steeper learning curve for users                                                        

Why gradient boosting?

Upsides:

  • Same reasons why I like Random Forests, plus...
  • Very good accuracy with fewer learners (greedy).
  • Excellent XGBoost implementation (R, Python).
  • Many model design options at reach.

 

Downsides:

  • Sequential by design, hence intrinsically slower to train than other methods like RF.
  • Hyperparameter tuning.

Hands-on

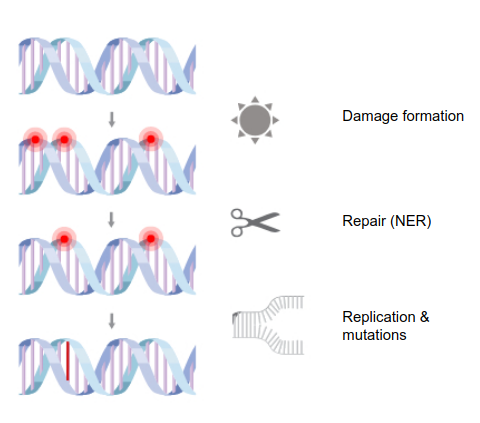
GB hands-on

Dataset: UV-induced CPD (cyclobutane pyrimidine dimer) in human skin fibroblasts

Samples: 1Mb chunks

Response: CPD counts per chunk

Covariates: Annotated coverage by chromatin-associated structures and enrichment of histone modifications enrichment.

GB hands-on

Challenges

Many covariates: from 20 to 1000+

Many interactions expected

Want accurate prediction without killing interpretation

Parameters

params = {

'objective': 'reg:linear',
'n_estimators':        15000,
'subsample':          0.5,
'colsample_bytree':          0.5,
'learning_rate':        0.001,
'max_depth':            4,

...             

}

Accuracy and CV

0.5 Fold

Accuracy

Partial model with single covariate (~ 0.3 Var Explained)

Full Model                                                (~ 0.9 Var Explained)

Feature Importance

Several choices in most frameworks

 

  • Number of splits each covariate contributes.
  • Gain: mean decrease of error every time a covariate is used in a split.
  • Permutation: how the error increases after "noising" a covariate.

  • Attribution: model the effect of each covariate in each sample.

Feature Importance

 

 

  • Number of splits each covariate contributes.
  • Gain: mean decrease of error every time a covariate is used in a split.
  • Permutation: how the error increases after "noising" a covariate.

  • Attribution models: model the effect of each covariate in each sample.

We use an attribution model based on

Shapley values (cooperative game theory)

"average effect of adding a feature to predict a given sample"

Feature Importance

Partial Dependence & Interaction

Example with H3K27ac

Kudos to...

  • Valiant (1984): PAC learning models 

  • Kearns and Valiant (1988): first to pose the question of whether a “weak” learning algorithm which performs just slightly better than random guessing [PAC] can be “boosted” into an arbitrarily accurate “strong” learning algorithm.

  • Schapire (1989): first provable polynomial-time boosting algorithm.

  • Freund (2000): improved efficiency and caveats.

  • Many others...

Kudos to...

References

  • Distributed Machine Learning Common Codebase https://xgboost.readthedocs.io/en/latest/model.html

  • Freund Y, Schapire R  A short introduction to boosting

  • Hastie T, Tibshirani R, Friedman J The Elements of Statistical Learning

  • Lundberg S, Lee S-I Consistent individualized feature attribution for tree ensembles

  • Natekin A, Knoll A Gradient boosting machines, a tutorial

Gradient boosting seminar at IRB

By Ferran Muiños

Made with Slides.com

Gradient boosting seminar at IRB

A gentle introduction to ensemble tree models and gradient boosting for regression. Presented at the BBG-SBNB joint seminar at IRB Barcelona.

  • 1,072

More from Ferran Muiños