Circuits 1
Current Direction

click here to move forward


click here for instructions
by Goncalo Martins
move backwards

Directions

move forward

don't use the blue arrows
(click me)

If you see a click me...
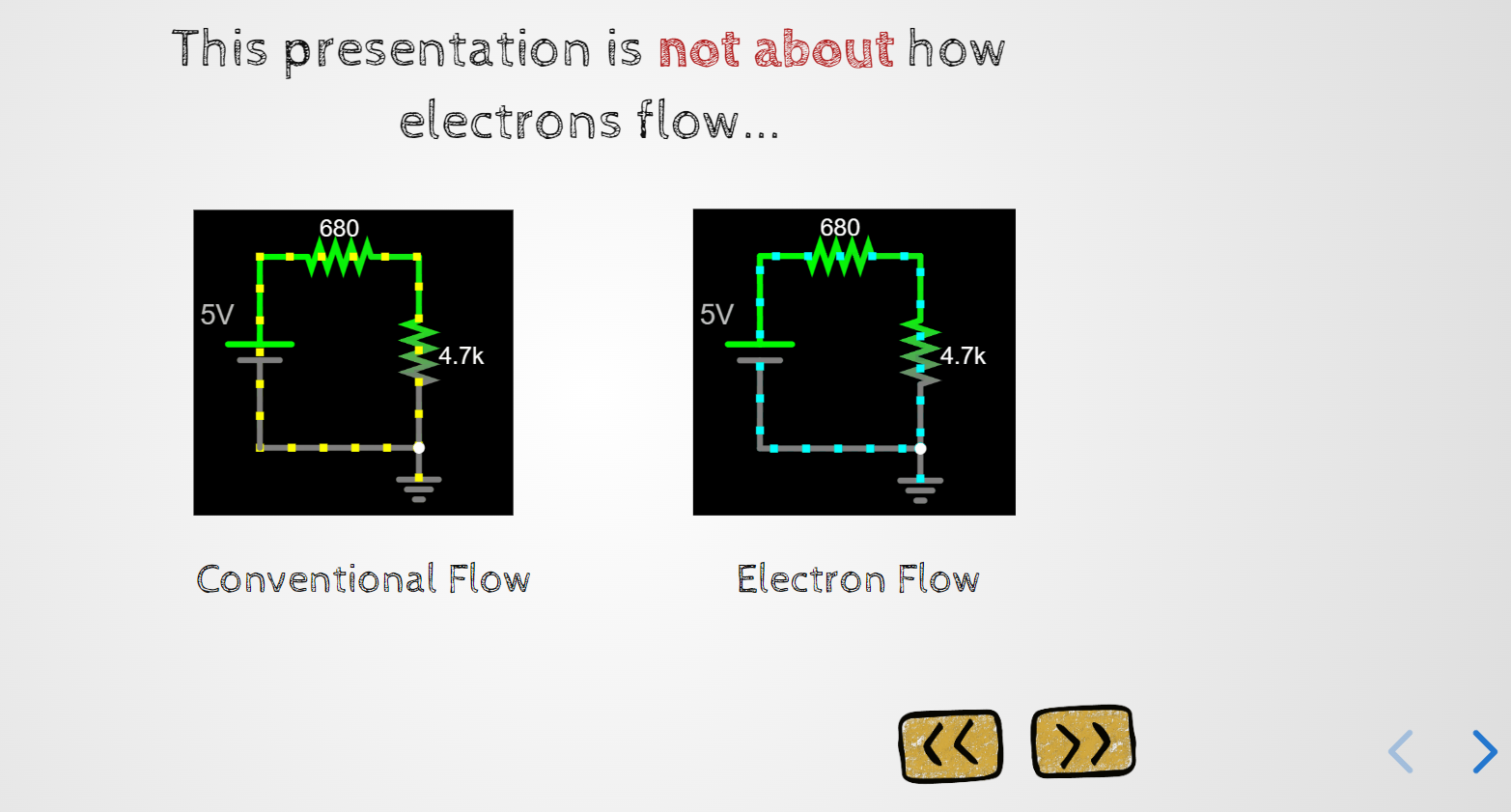
This presentation is not about how electrons flow...
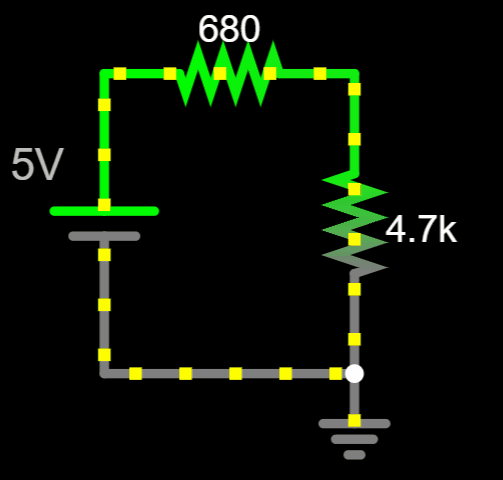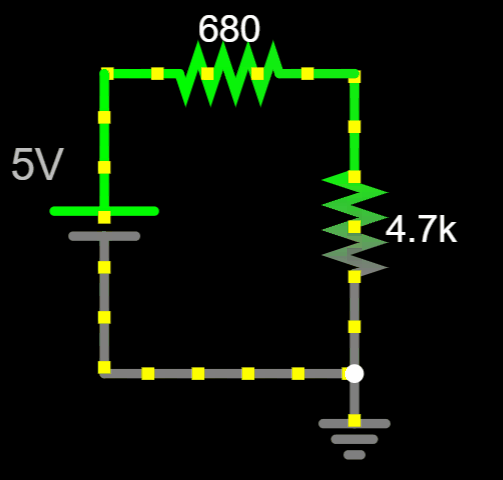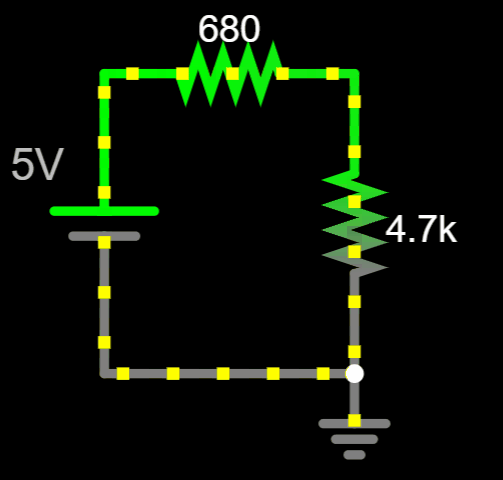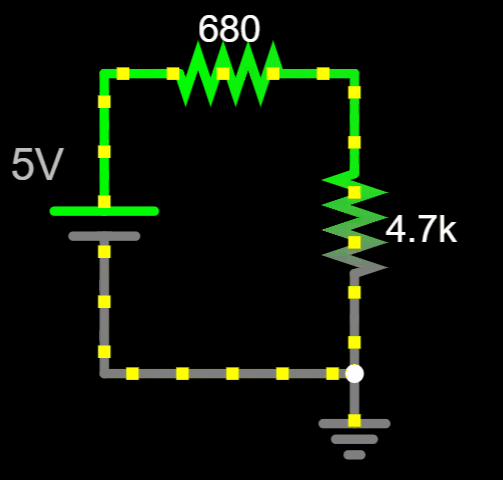
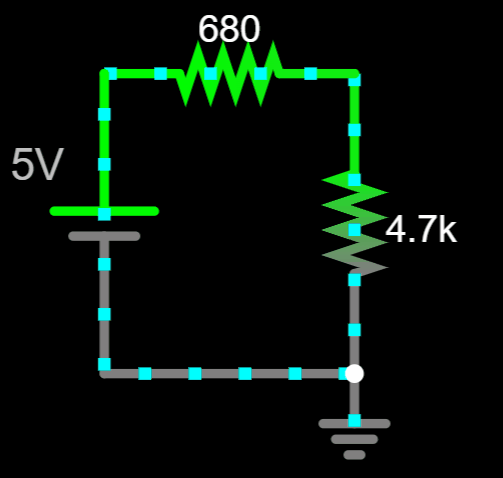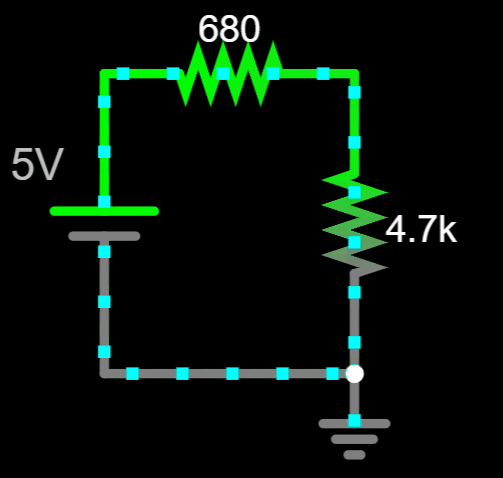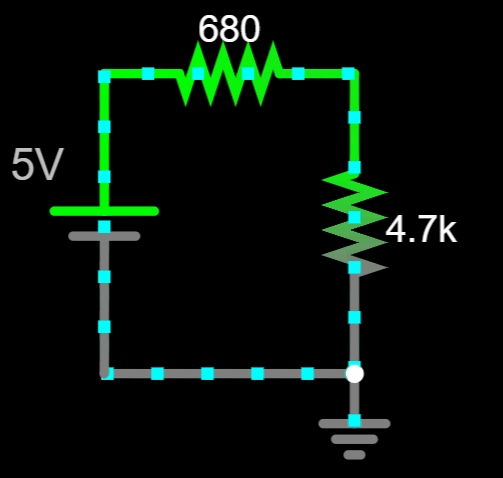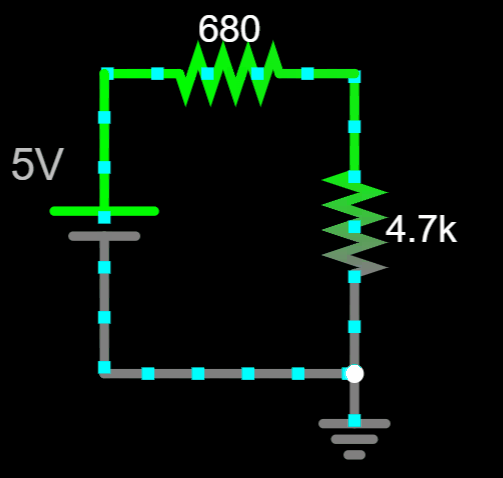
Conventional Flow
Electron Flow
This presentation is about understanding current
directions in a circuit while analyzing it.
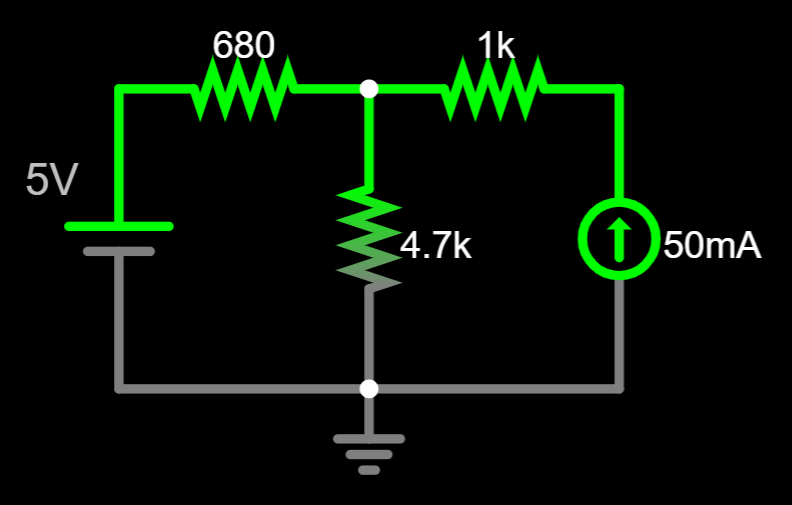



Which direction should we pick?
Before answering that question, let's review a couple of rules...
(click me)
(click me)


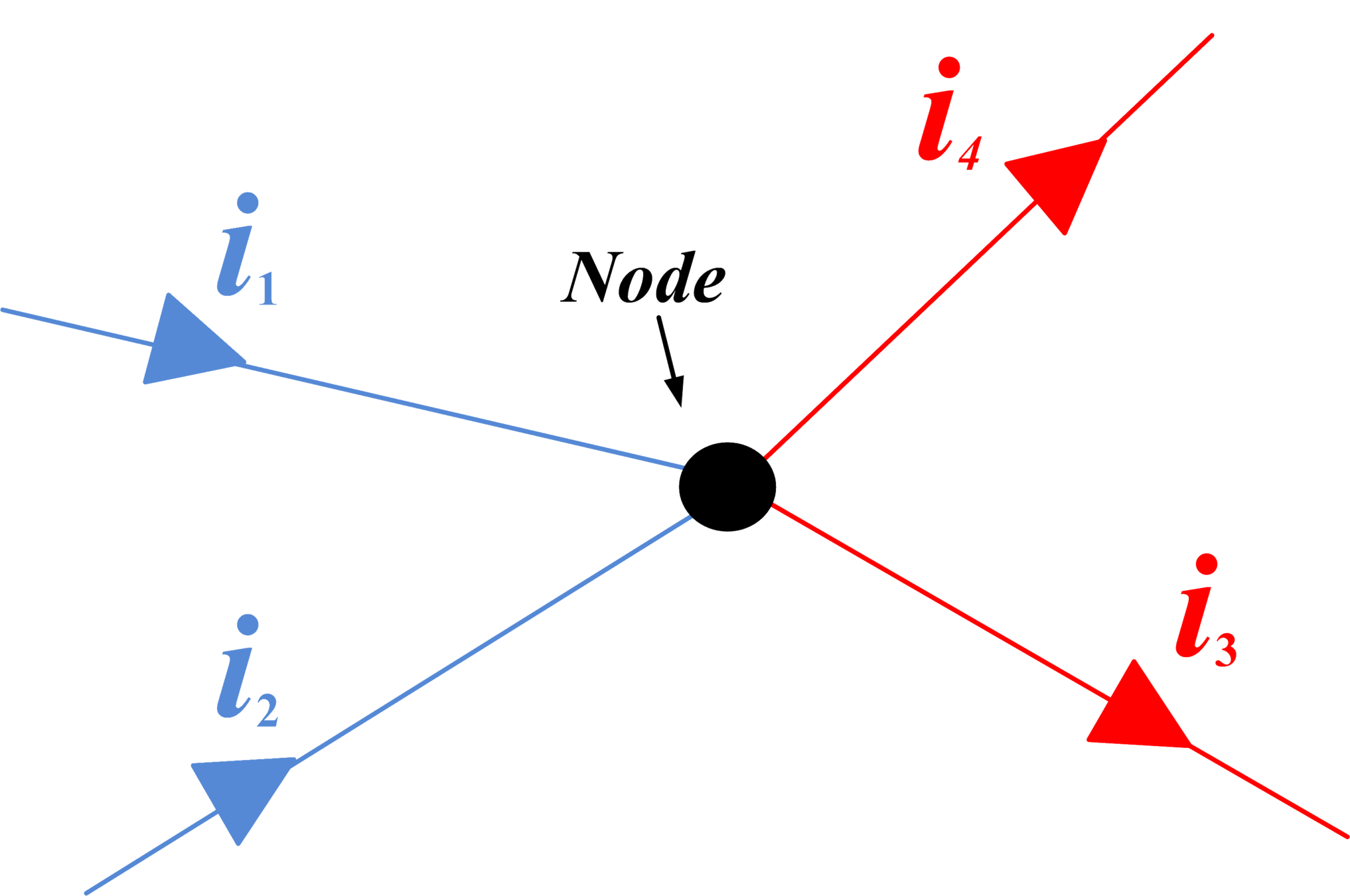
The sum of currents entering a node...
is equal to the sum of currents leaving the node.
Kirchhoff's Current Law
(KCL)
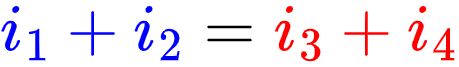
(click on the node)
Passive Sign Example...


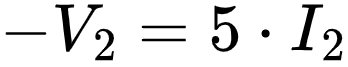
(click on the voltage drop)

KCL Example...
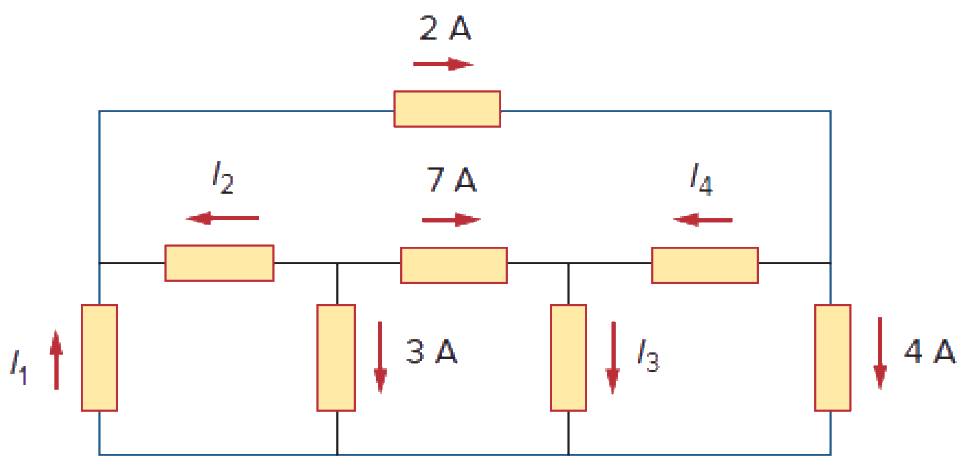
(click on the nodes)

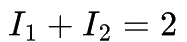
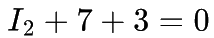
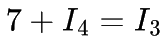


Passive Sign Convention
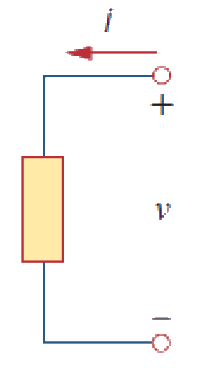
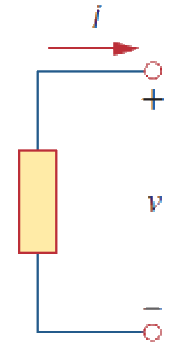
Current entering the positive terminal...
Current entering the negative terminal...
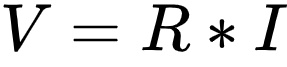
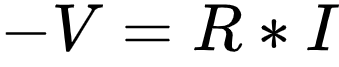
... has a positive voltage drop.
... has a negative voltage drop.
(click on the voltage drop)

Let's cover an example where all
these concepts are connected together...
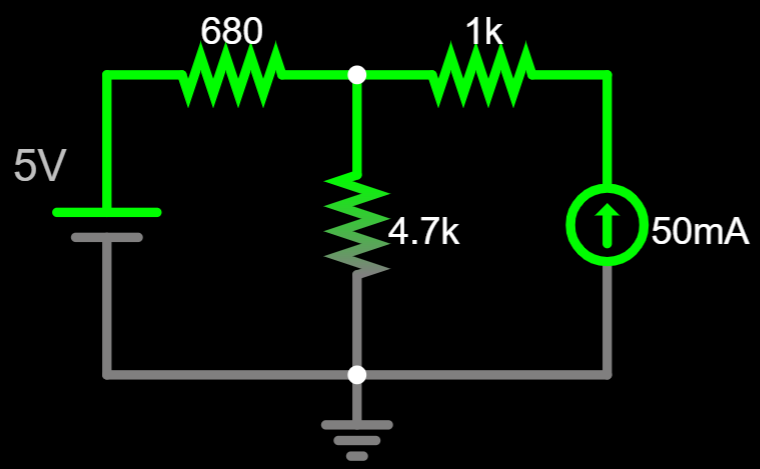
(circuit link)
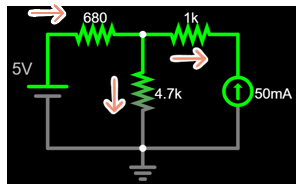
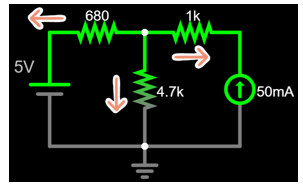
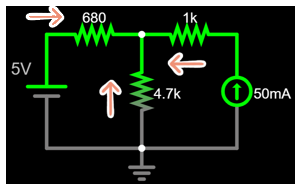
Notice there are no signs or currents
assigned in this circuit...

Start by choosing any direction of current that you want, and don't overthink...



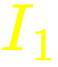
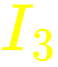

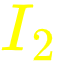
Assign + and - around the resistors.
Don't overthink here neither...




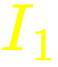
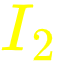
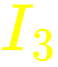



+
+
+
-
-
-
Hint: it makes it easier if you assign passive convention, but you don't need to.
From now on, apply KCL and passive sign to get the equations out of the circuit.




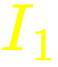
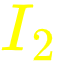
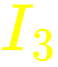



+
+
+
-
-
-
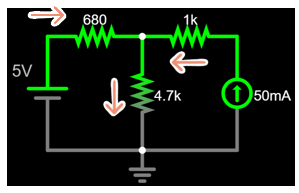
To make things less cluttered...
The analysis will be split into 2 schematics.


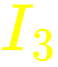



+
+
+
-
-
-



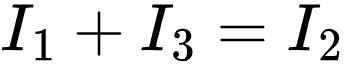
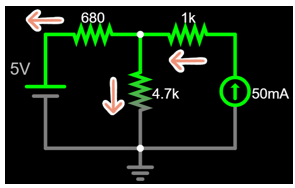
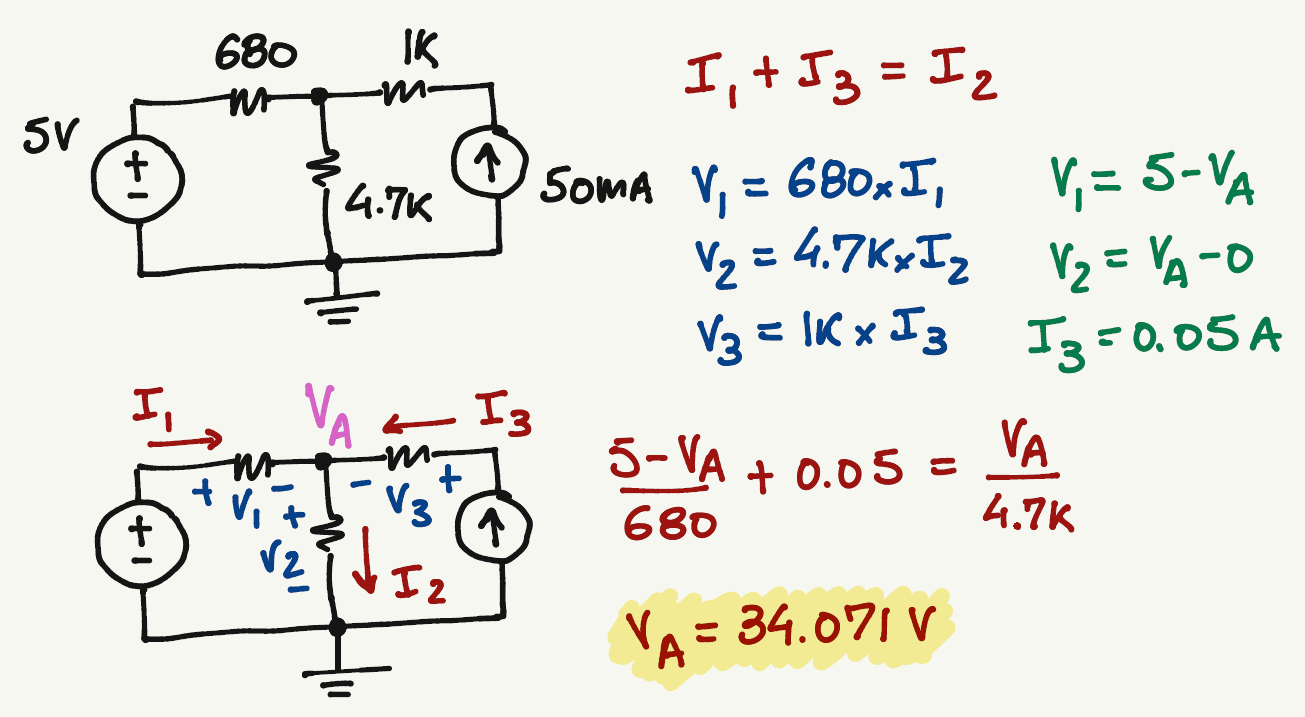
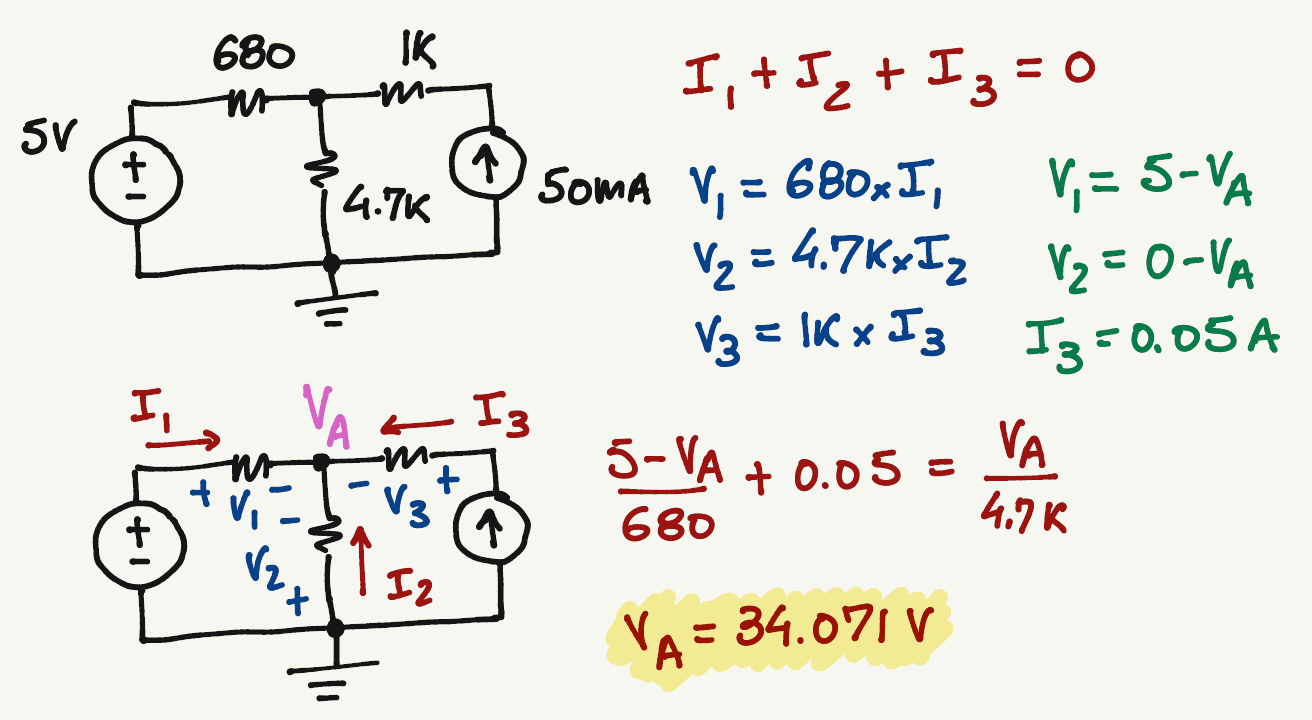
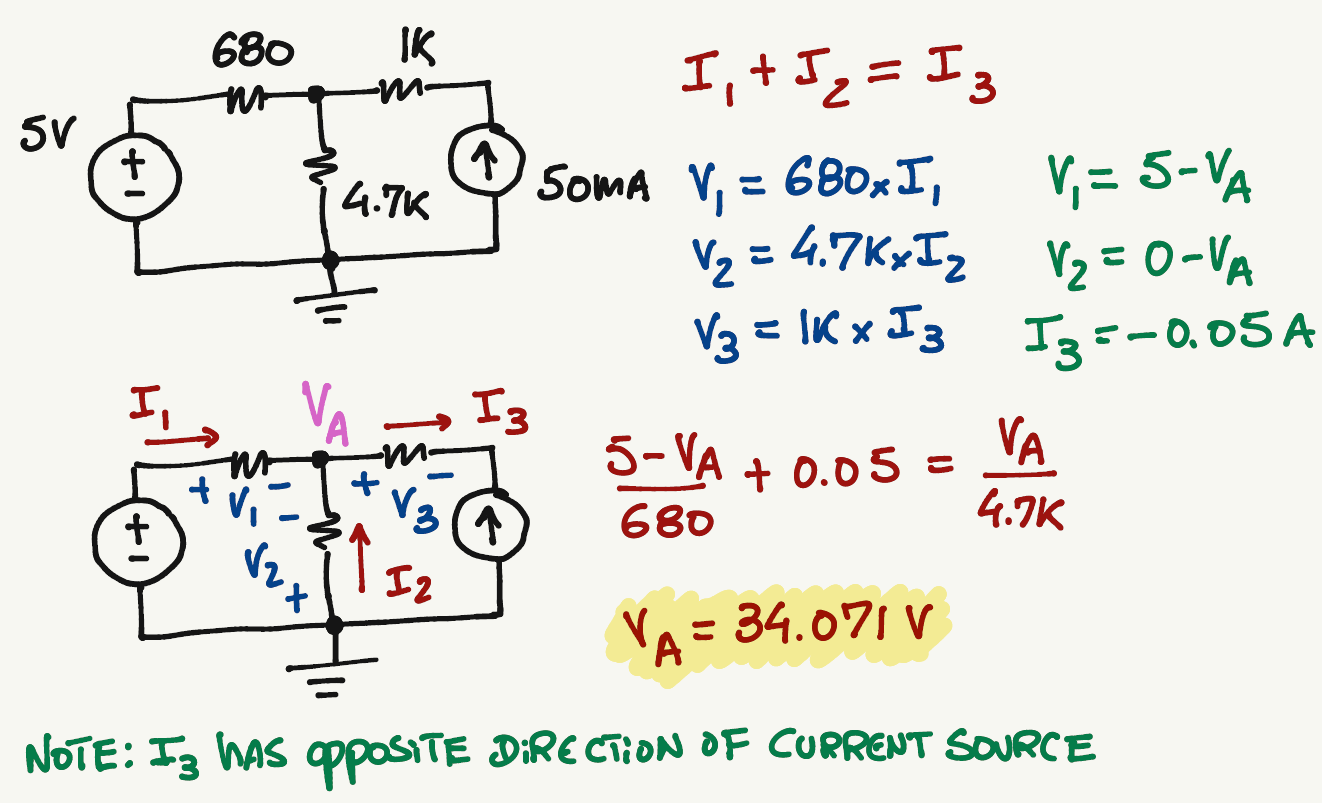
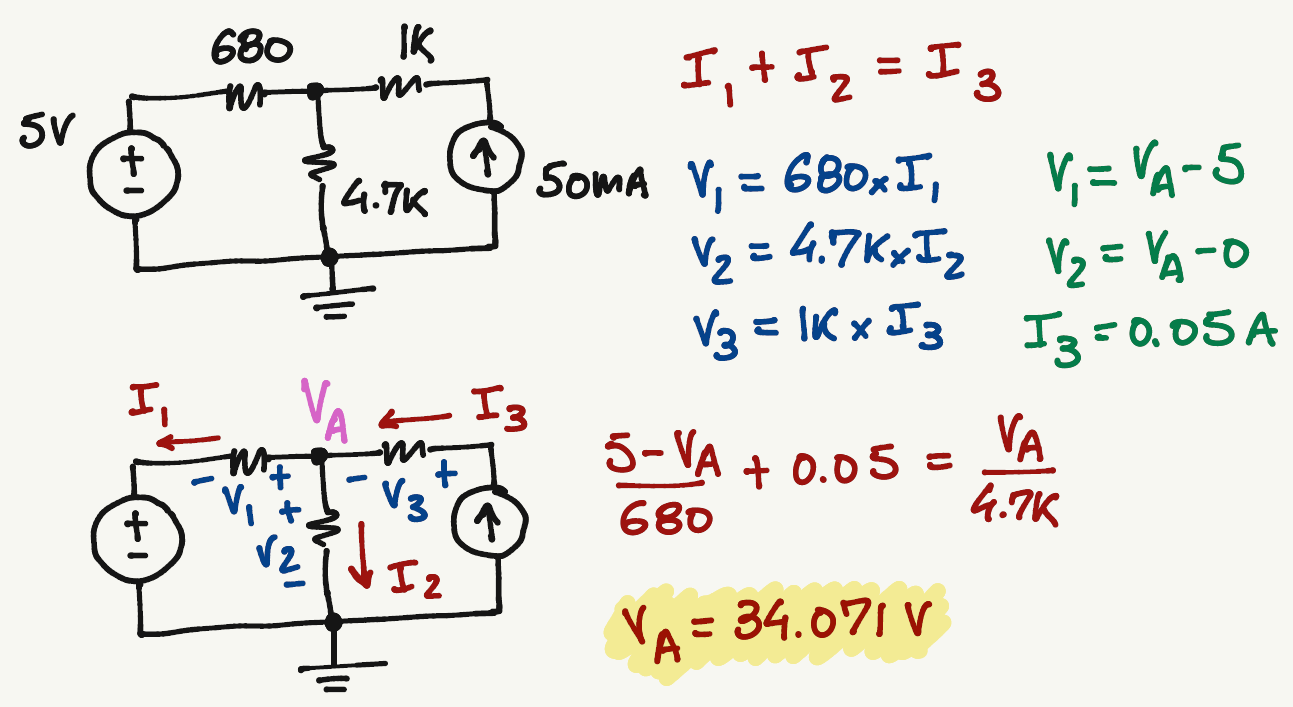
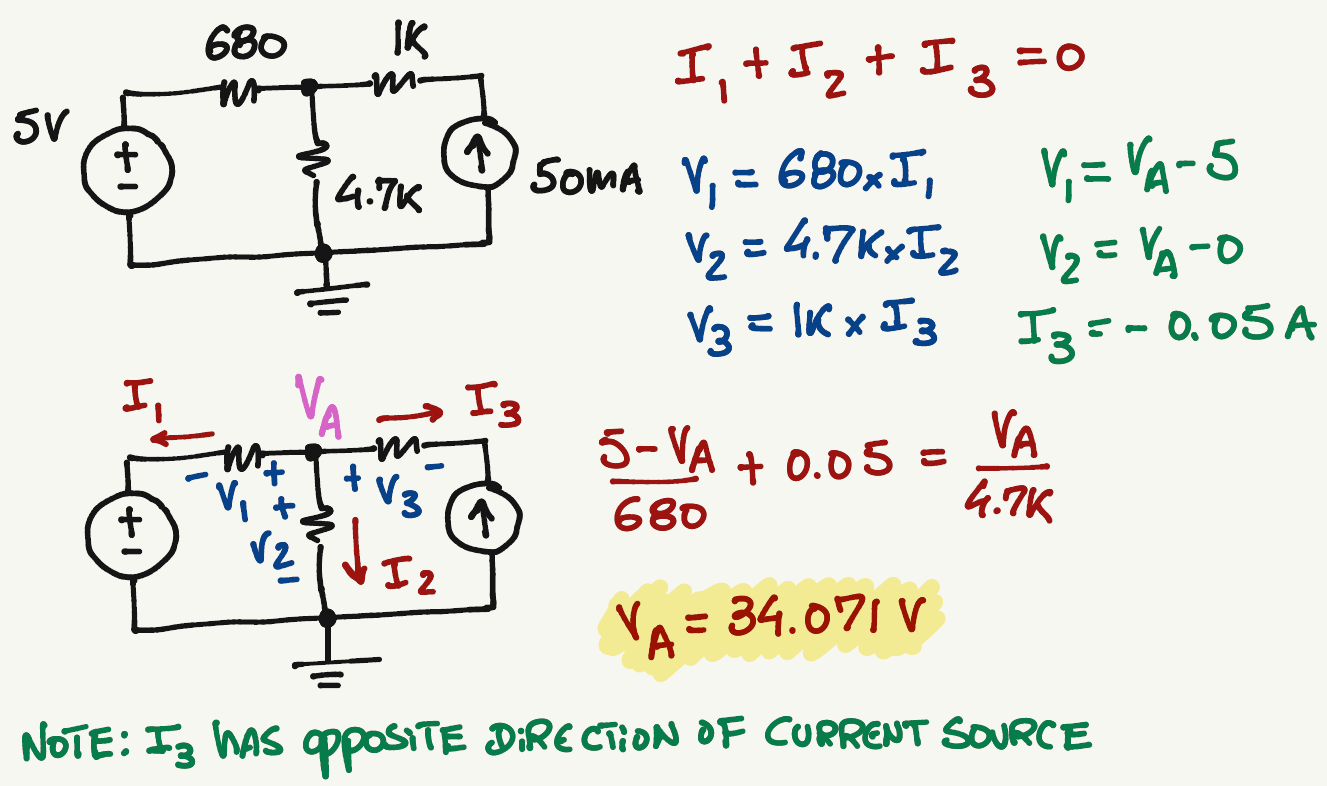
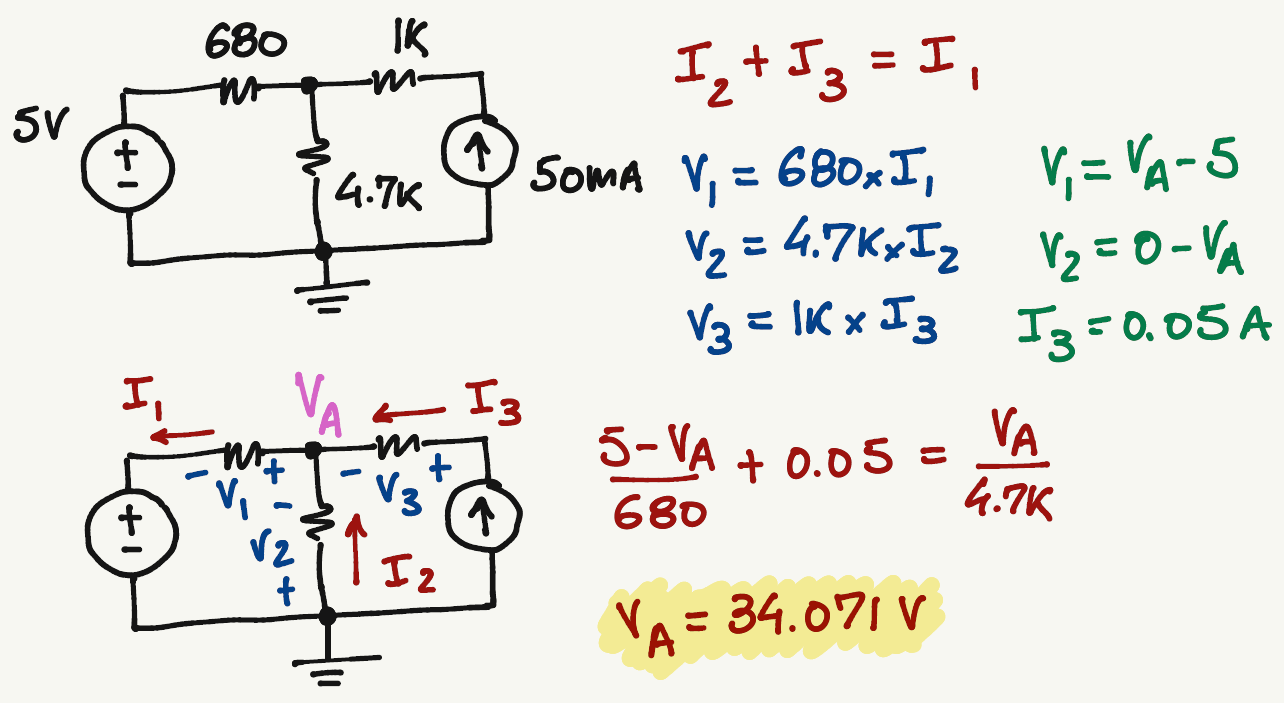
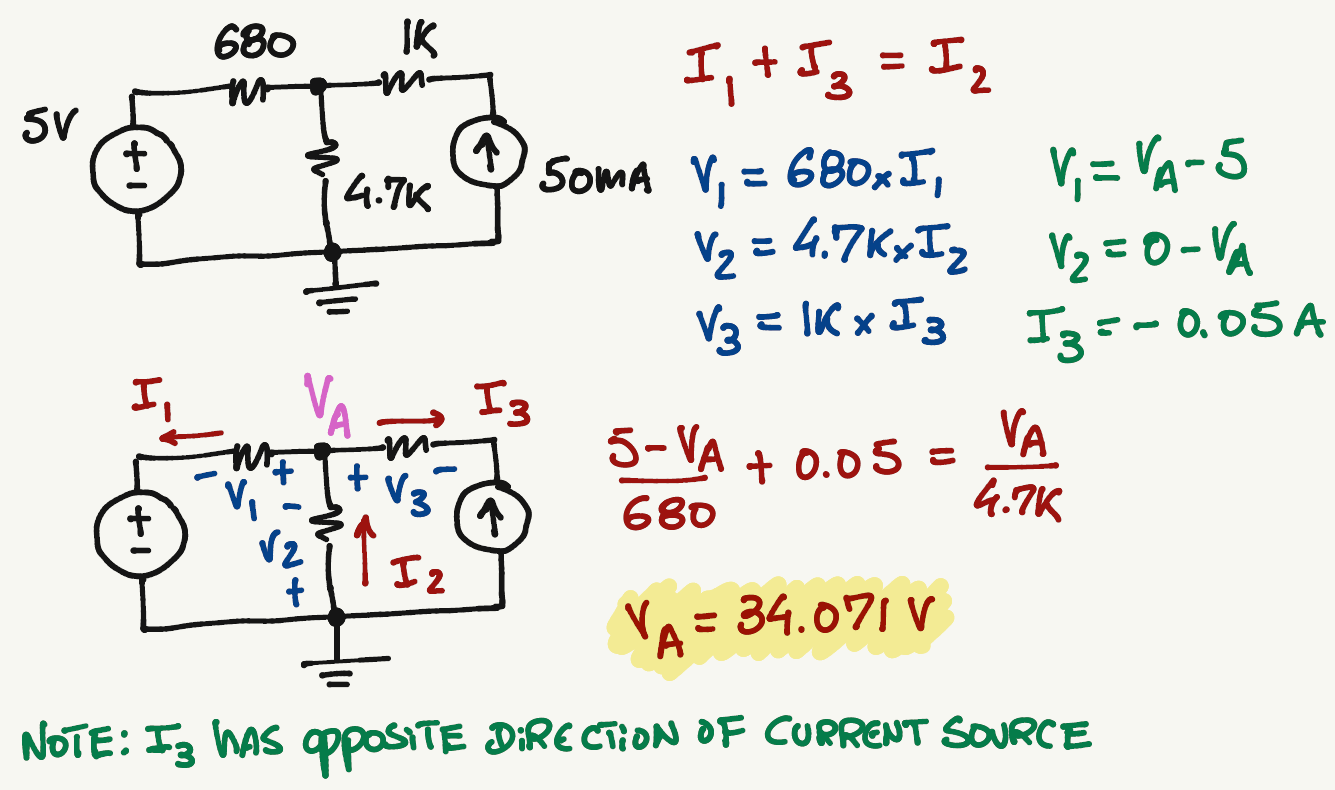
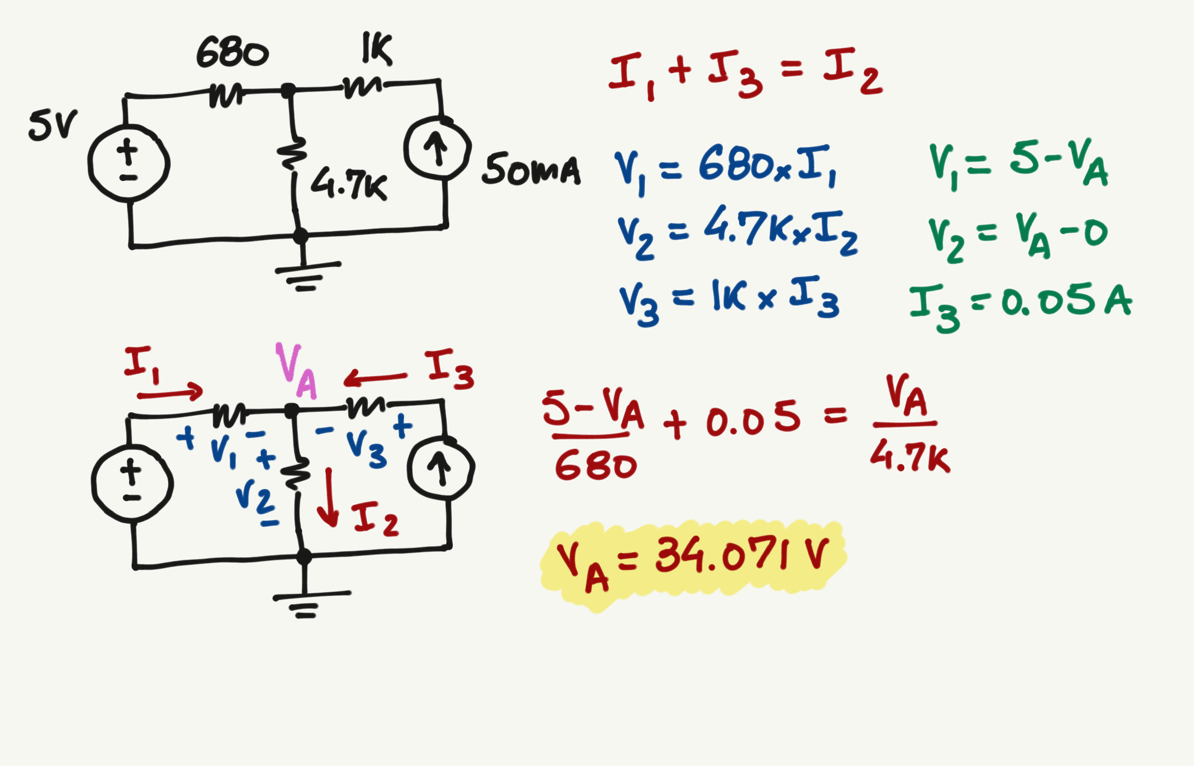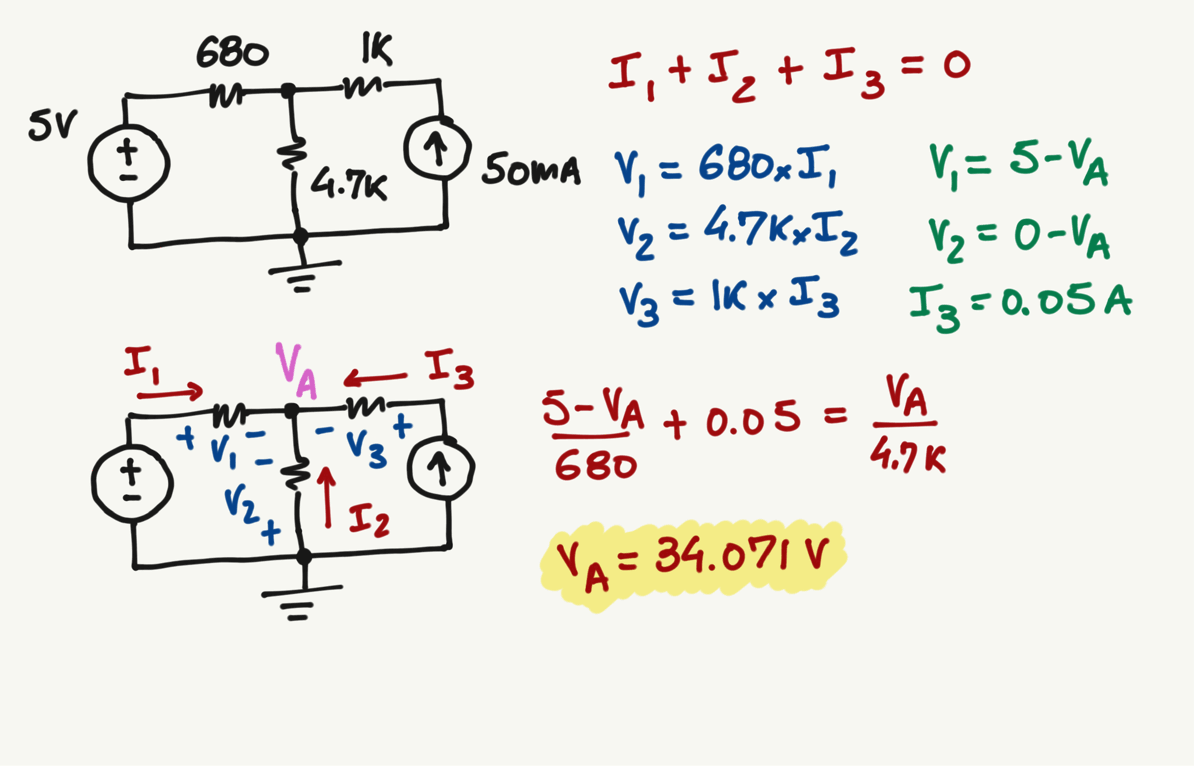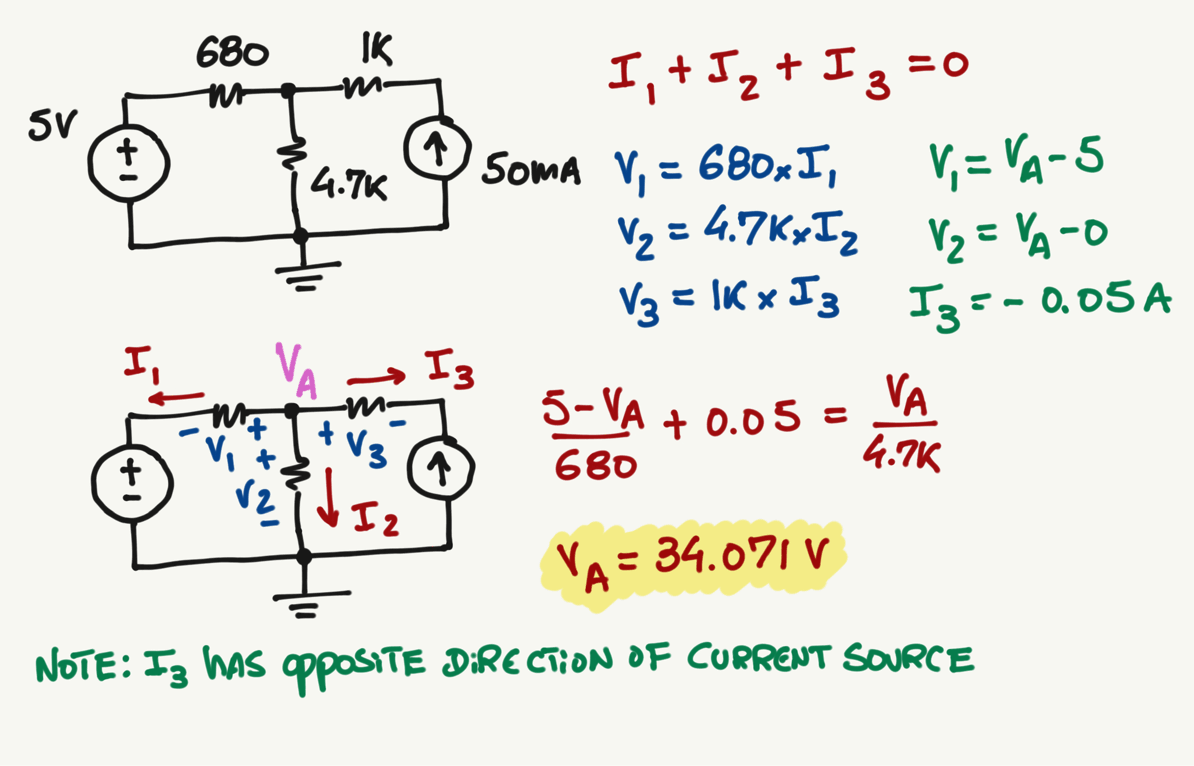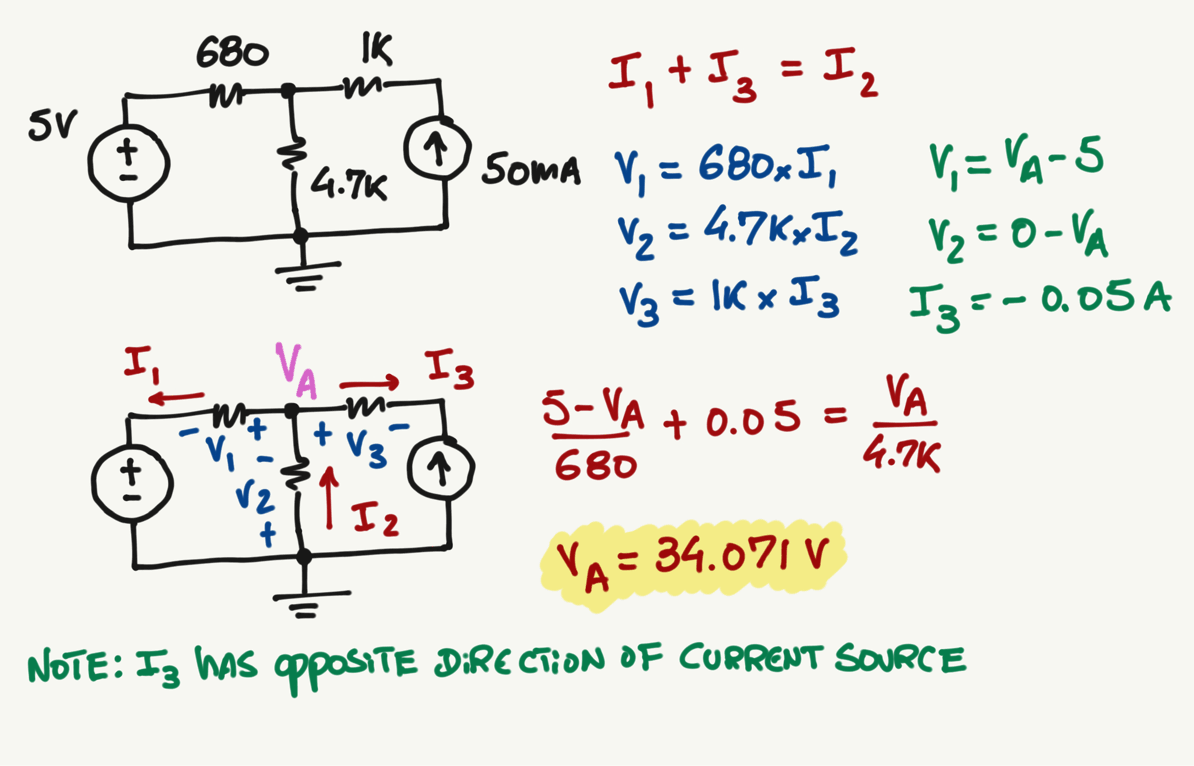
A
KCL at A:



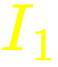
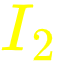



+
+
+
-
-
-



Passive Sign:
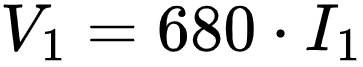
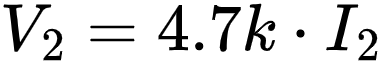
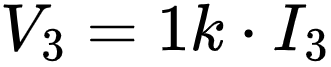
I_3=0.05 A

(click here)



+
+
+
-
-
-

Passive Sign:
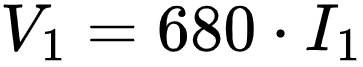
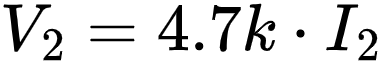
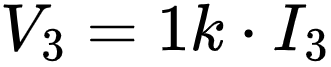
Voltage Differential:
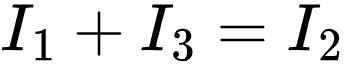
KCL at A:

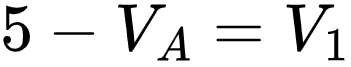
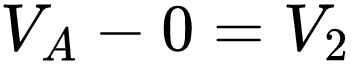
We can write \(V_1\) and \(V_2\) in terms of \(V_A\)
V_A

For this particular case, we don't need to worry about \(V_3\) since we already know the value of \(I_3\)
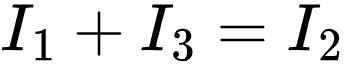
KCL at A:
Passive Sign:
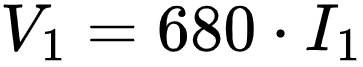
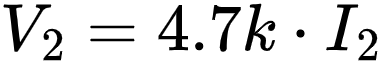
\frac{V_1}{680}+0.05=\frac{V_2}{4.7k}
Step 1:
Substitute EQs A into KCL
Step 2:
Substitute EQs B into Step 1


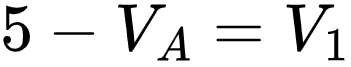
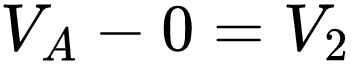
Voltage Differential:
\frac{5-V_A}{680}+0.05=\frac{V_A-0}{4.7k}
(EQs A)
(EQs B)
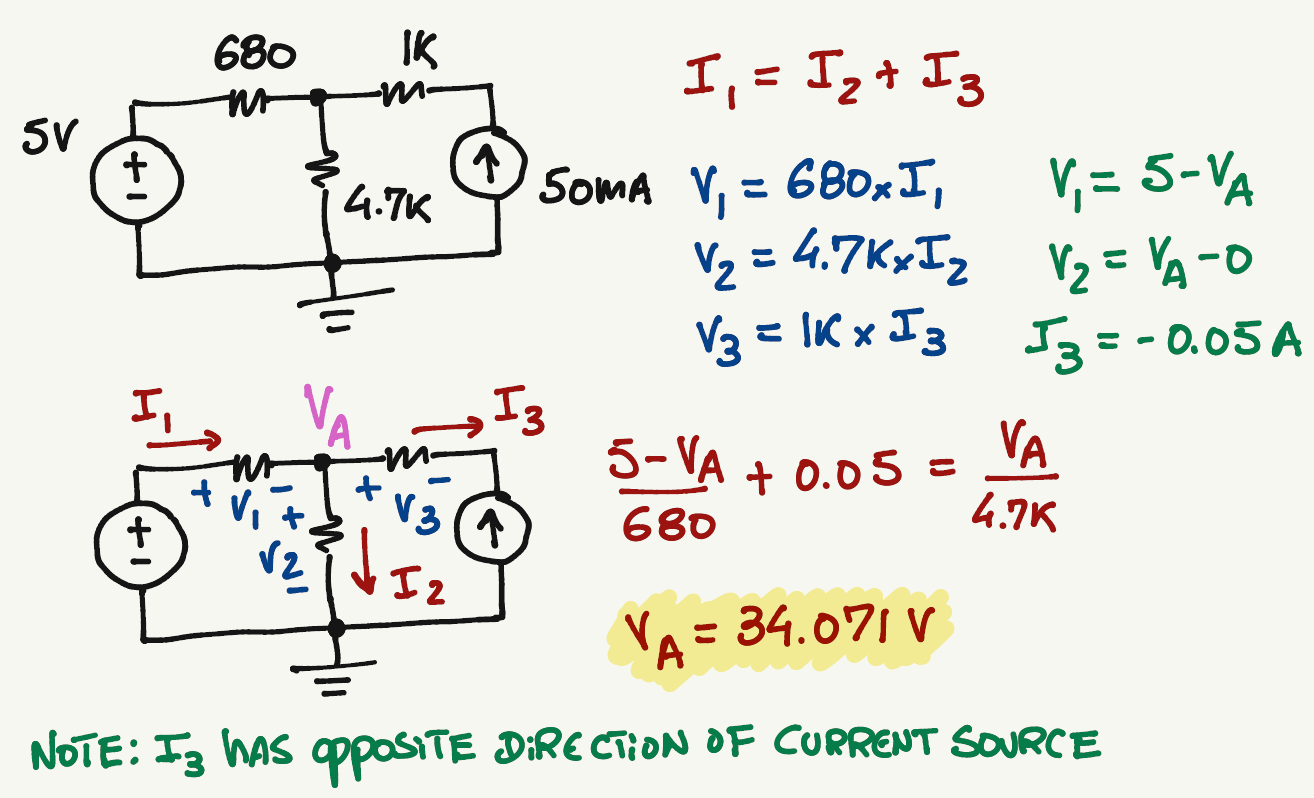
I_3=0.05 A
Step 3:

Solve for \(V_A\)
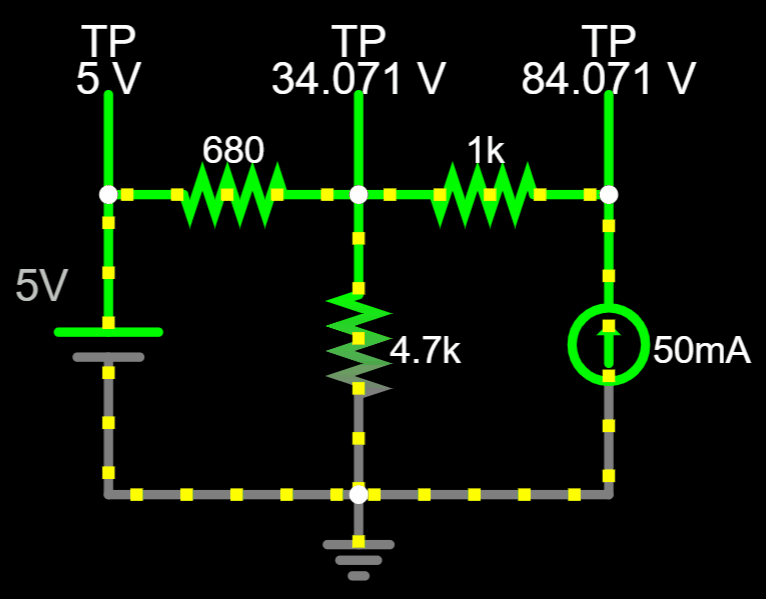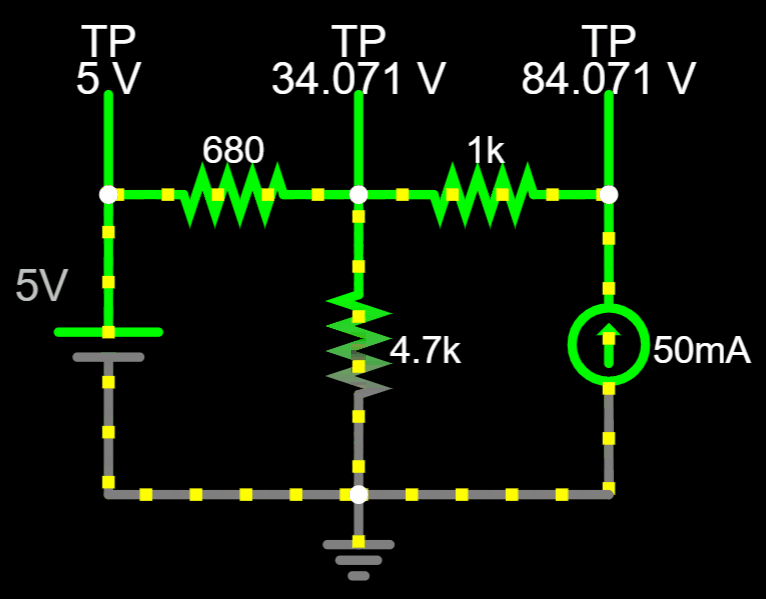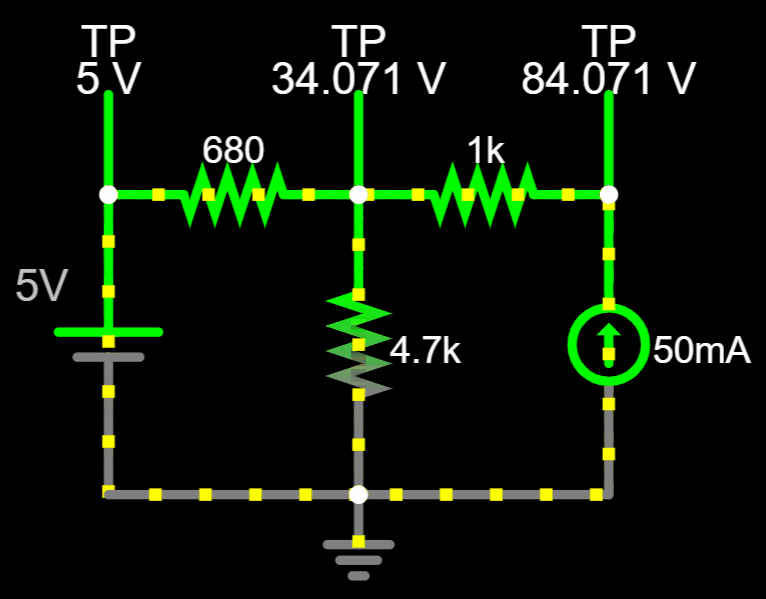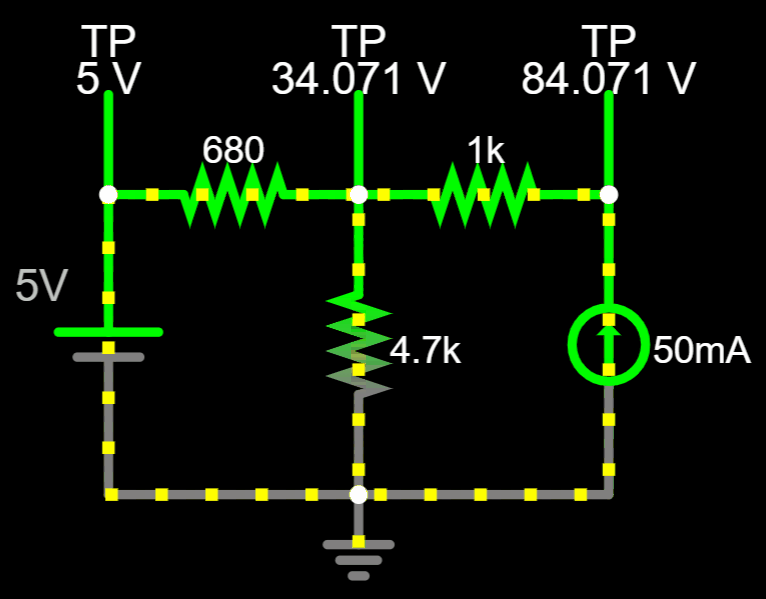
V_A=34.071 \> V
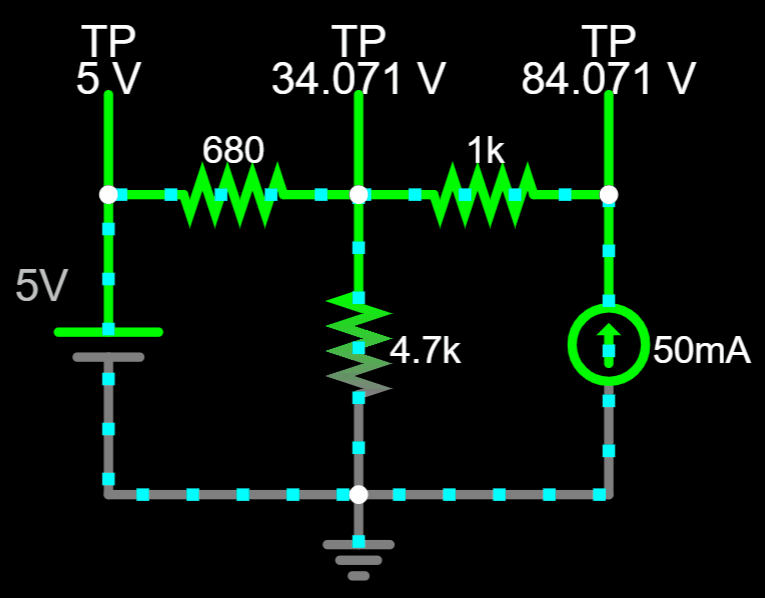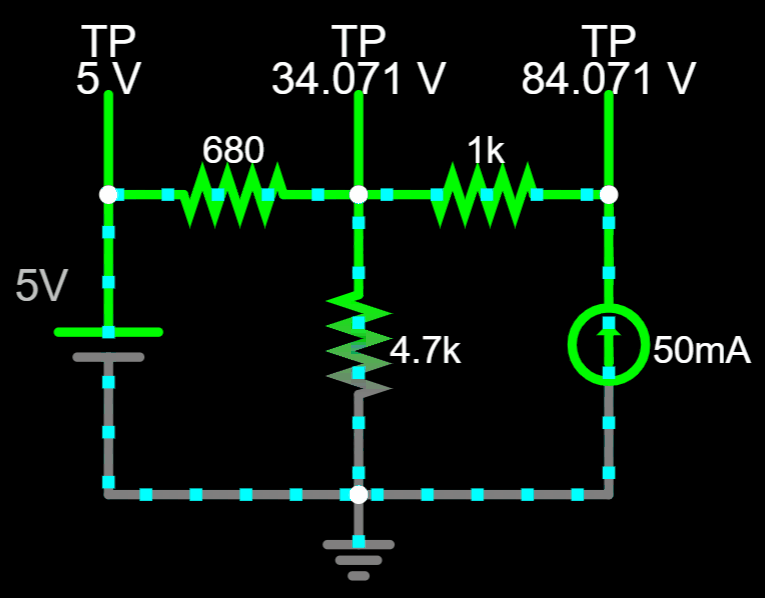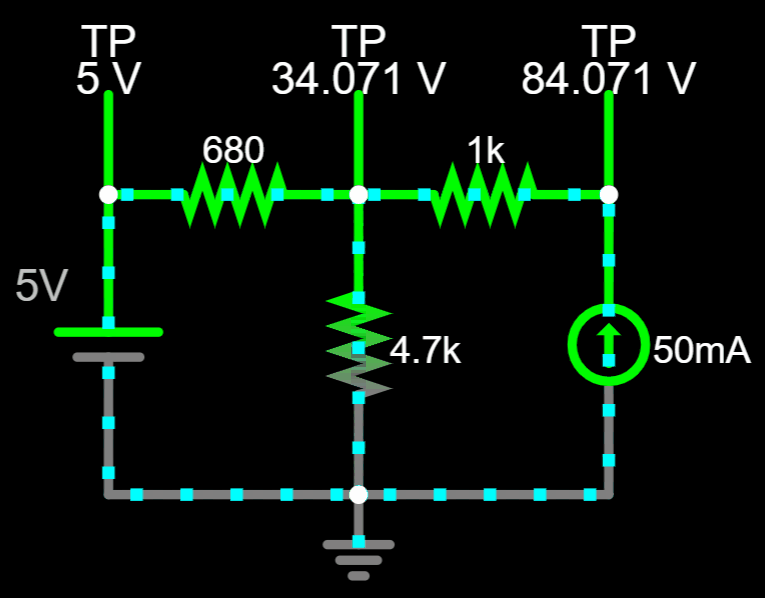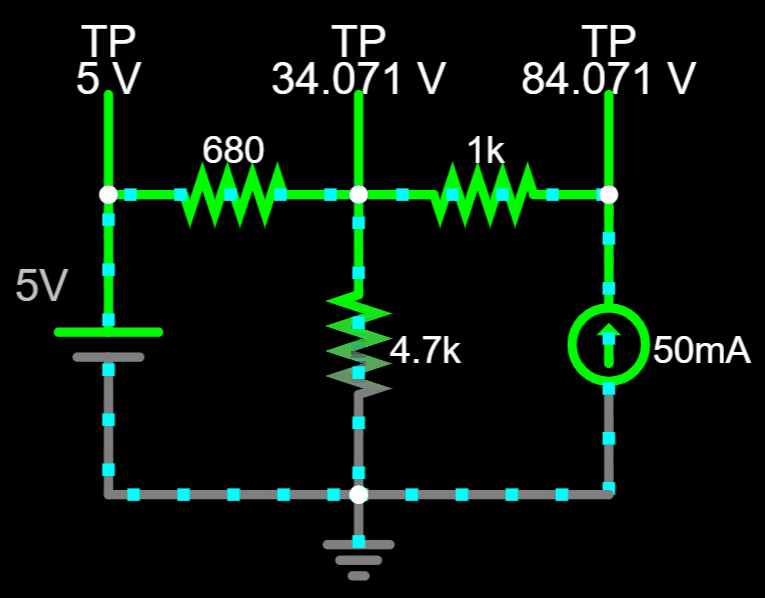
Now that we have \(V_A\)...
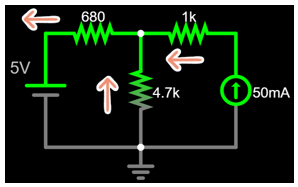
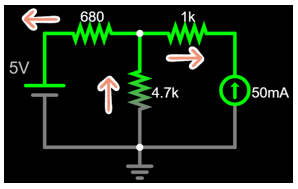
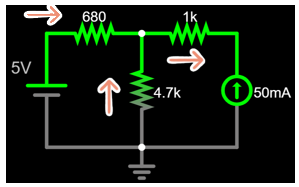
You can adjust and see the real direction of the currents.
Conventional Flow
Electron Flow






No matter which combination of currents you pick, the value of \(V_A\) will always be the same...
Summary
-
Adjust the direction of the currents accordingly.
-
Apply any direction of currents in your circuit.

(hover here)
-
Find all the voltages in your circuit.
(Don't Overthink)
current_direction
By Goncalo Martins
current_direction
- 619