MATERIALS AND PLATFORMS FOR AI
WHO AM I?
Giovanni Pellegrini
Associate Professor - Physics Department - University of Pavia
Research Interests
-
Computational Nanophotonics
-
Machine Learning and Optimization for Nanophotonics
-
Machine Learning for Image Reconstruction
-
Machine Learning for Signal Processing
Also interested in
-
Industrial Automation and Robotics
-
Deep Learning for Machine Vision
IMAGE RECONSTRUCTION: 1
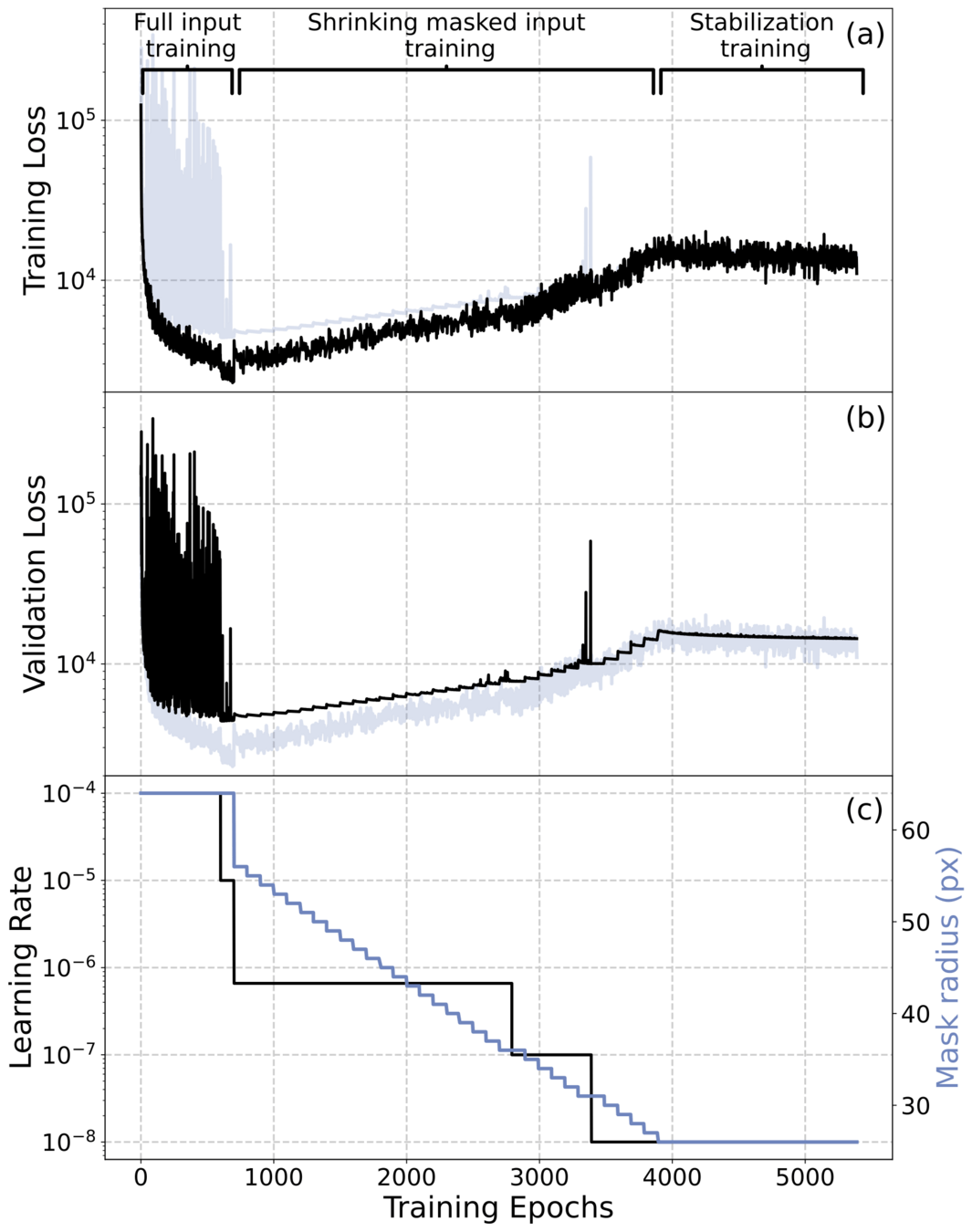

IMAGE RECONSTRUCTION: 2
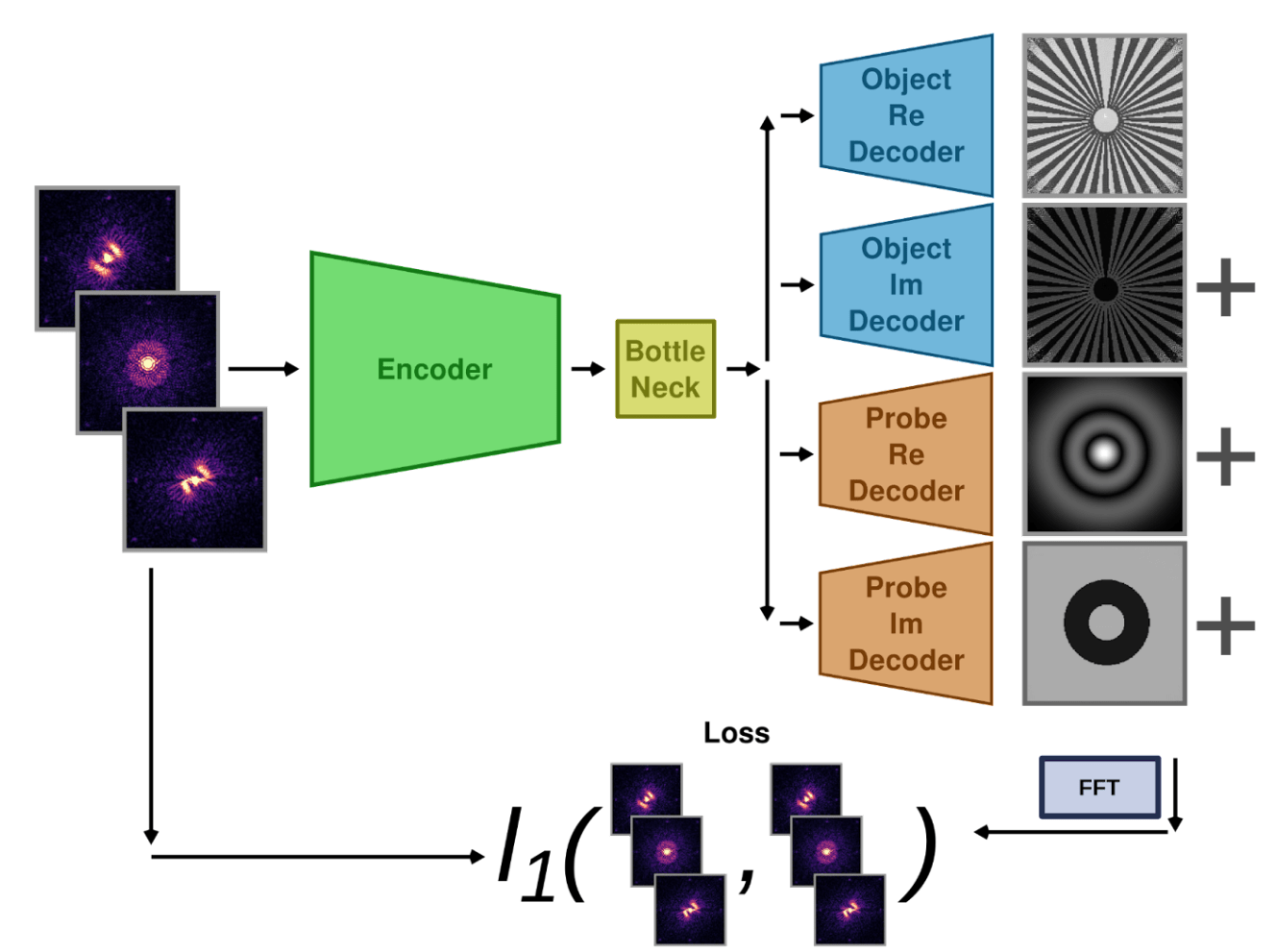
QUESTION 1: KNOWLEDGE
QUESTION 1: KNOWLEDGE
- physics-informed neural networks
- how AI is exploited for materials research
- how semiconductors are used in tech, from the physical point of view.
- I would like to understand more about hardware part of computer. In particular, I am interested in how cpu and gpu are made and if it is possible I am also interested in quantum computer
- Understand how chips are made and work, the properties of silicon. In general a more technical and engineering point of view of AI. Also maybe the impact of ai on the environment
- How modern computing devices are built
- Learn how different models perform on different hardware, why and how to optimize results for a given machine.
- I expect to understand thanks to which medium artificial intelligence propagates and how it is effectively applied to different fields, not only theoretically.
- Deeper knowledge of physical concepts and fundamentals of platforms and materials used for AI applications.
- I expect to be able to reconstruct images better than mathematics for imaging and signal processing course
- Learn how light and physical phenomena can be simulated with Deep learning and neural network. What are it's pros and cons
- Understanding of the basics of physical implementation of AI
- The integration part with AI
- Something related to the materials used by AI infrastructures
- Better understanding on how the machines receive and process informations. Which are the limits and the point of strength on which we should concentrate when we write a code
- I would be interested in knowing how sensors of ATLAS from CMS work, in particular i am curious about things like ECAL or HCAL.
QUESTION 2: SKILLS
QUESTION 2: SKILLS
- Solve differential equations computationally using neural networks
- I am interested in CUDA toolkit.
- algorithms and state of the art techniques about ML and DL relevant in the field.
- being able to approach coding solutions to physical problems
- better use of fourier transforms and other mathematical tools not just on the “mathematical side” but in programming
- More useful usage of fourier transform
- i expect to gain more physics knowledge applied to computer science. However, I expect to end the course with solid theoretical bases on the presented topics.
- Learn how to integrate our code in more practical situations and applications
- ability to recognize and encode the features of physics problems
- I am particularly interested in semiconductors. I am not sure if we will cover the physical chemistry aspect of the semiconductor elements but it is also a very interesting topic to me. I would like to see how these topics can be implemented in deep learning models.
- design of physical systems
- Ability to apply practically with neuroal networks the theoretical concepts
- Knowledge about how to use specific material for the porpoise of AI
QUESTION 3: LABS
NON-LINEARITIES & LOGIC GATES
x_{2}
x_{1}
NON-LINEARITIES & LOGIC GATES
x_{2}
x_{1}
x_{1} \; \mathrm{\mathbf{XNOR}} \; x_{2}
(x_{1}=1,x_{2}=1)
(x_{1}=1,x_{2}=0)
(x_{1}=0,x_{2}=0)
(x_{1}=0,x_{2}=1)
NON-LINEARITIES & LOGIC GATES

x_{1} \; \mathrm{\mathbf{AND}} \; x_{2}
x_{1}
x_{2}
1
h_{\Theta}(x)
x_{1}
x_{2}
h_{\Theta}(x)
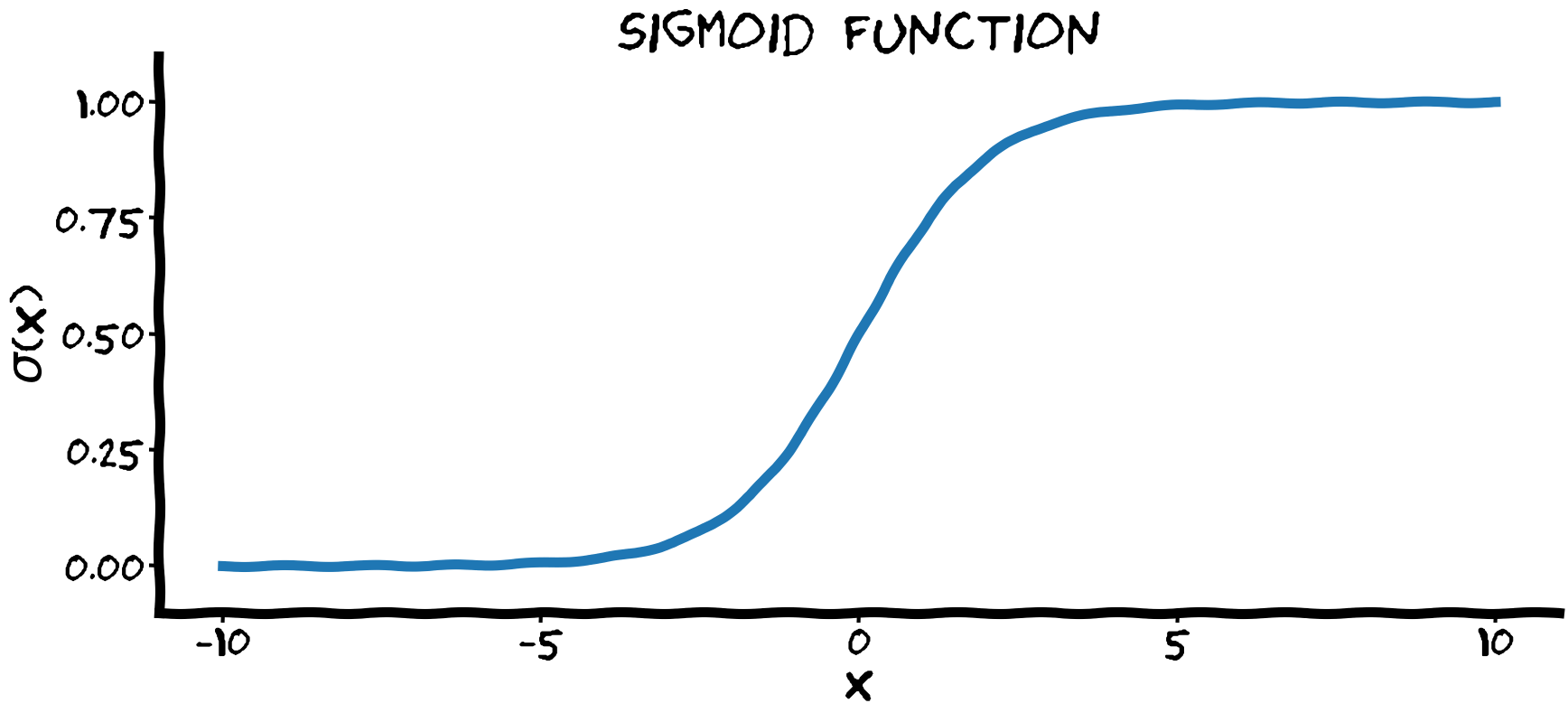
NON-LINEARITIES & LOGIC GATES

x_{1} \; \mathrm{\mathbf{OR}} \; x_{2}
x_{1}
x_{2}
1
h_{\Theta}(x)
x_{1}
x_{2}
h_{\Theta}(x)
NON-LINEARITIES & LOGIC GATES
\mathrm{\mathbf{NOT}}(x_{1})
x_{1}
1

h_{\Theta}(x)
x_{1}
h_{\Theta}(x)
NON-LINEARITIES & LOGIC GATES

\mathrm{\mathbf{NOT}}(x_{1}) \; \mathrm{\mathbf{AND}} \; \mathrm{\mathbf{NOT}}(x_{2})
x_{1}
x_{2}
1
h_{\Theta}(x)
x_{1}
x_{2}
h_{\Theta}(x)
NON-LINEARITIES & LOGIC GATES
x_{1} \; \mathrm{\mathbf{XNOR}} \; x_{2}
x_{1}
x_{2}
1

a^{(1)}_{1}
a^{(1)}_{2}
1
h_{\Theta}(x)
x_{1}
x_{2}
h_{\Theta}(x)
a^{(1)}_{1}
a^{(1)}_{2}
LINEAR CIRCUIT ELEMENTS


\( R_{tot} = R_{1} + R_{2} \)
\( V = I \, R_{tot} \)
\( V = I \, R_{tot} \)
R_{tot} = \frac{R_{1} \, R_{2}}{R_{1} + R_{2}}
LINEAR CIRCUIT ELEMENTS
\[ X_{R} = R \]
\[ V = I \, X_{R} \]
\[ X_{C} = \frac{1}{i \,\omega \, C} \]
\[ V = I \, X_{C} \]
\[ X_{L} = i \,\omega \, L \]
\[ V = I \, X_{L} \]



TOWARDS LOGIC GATES





MATERIALS AND PLATFORMS FOR AI

Semiconductors
MATERIALS AND PLATFORMS FOR AI



Si
7
28.085
Silicon
GROUP IV SEMICONDUCTORS
MATERIALS AND PLATFORMS FOR AI
III-V AND II-VI SEMICONDUCTORS

GaN

GaAs


II
VI
III
IV
V

CdSe

ZnS
III-V
II-VI
MATERIALS AND PLATFORMS FOR AI


GPU
-
80 billions transistors in a H100 Hopper GPU
-
76 billions in a RTX 4090 GPU
-
208 billions in a B200 GPU
TRANSISTORS
MATERIALS AND PLATFORMS FOR AI
MATERIALS AND PLATFORMS FOR AI
MATERIALS
PLATFORMS

Si
7
28.085
Silicon
From the physics of semiconductors to the properties of solid state devices such as diodes and transistors
The physics of semiconductors with particular focus on their electronic transport properties


MATERIALS AND PLATFORMS FOR AI: OUTLINE
-
REVISION
-
WAVE THEORY AND CONNECTIONS TO FOURIER TRANSFORM
-
NEWTONIAN MECHANICS
-
HAMILTONIAN MECHANICS
-
QUANTUM MECHANICS
-
-
ELECTRONIC PROPERTIES OF MATERIALS
-
SOLID STATE DEVICES
MATERIALS AND PLATFORMS FOR AI: RESOURCES
-
SLIDES (ANNOTATED)
-
LECTURES RECORDINGS
-
SUGGESTED BOOKS
-
Kittel, Charles, and Paul McEuen. Introduction to solid state physics. John Wiley & Sons, 2018.
-
Ashcroft, Neil W., and N. David Mermin. Solid state physics. Cengage Learning, 2022.
-
Pierret, Robert F. Semiconductor device fundamentals. Pearson Education India, 1996.
-
Streetman, Ben G., and Sanjay Banerjee. Solid state electronic devices. Pearson, 2014.
-
-
ONLINE MATERIALS
-
RECEIVING HOURS: FRIDAY FROM 14.30 TO 15.30 ON ZOOM
MATERIALS AND PLATFORMS FOR AI: EXAMS
-
Multiple choice questions
-
Some of the multiple choice questions will require the solution of simple problems
-
The written exam can be integrated with an oral exam at the discretion of the teacher
MATERIALS AND PLATFORMS FOR AI: PHILOSOPHY
-
MATHEMATICALLY INTENSIVE CLASS
-
FOCUS ON NUMERICAL COMPUTATIONS
-
Fast Fourier Transforms
-
Numerical Linear Algebra (eigenproblems, solution of linear systems, etc...)
-
Physics Informed Neural Networks
-
Finite element methods (maybe)
-
-
GOOGLE COLAB AS DEFAULT PLATFORM
-
TIGHT FEEDBACK LOOP
MATERIALS AND PLATFORMS FOR AI: EVALUATIONS
2
1
-
Insufficient preliminary knowledge
-
Too much material for 6 credits
-
Interest in the topic
2
Materials and Platforms for AI - Introduction
By Giovanni Pellegrini
Materials and Platforms for AI - Introduction
- 175



