WAVE THEORY
TRANSVERSE AND LONGITUDINAL WAVES
TRANSVERSE WAVES
LONGITUDINAL WAVES
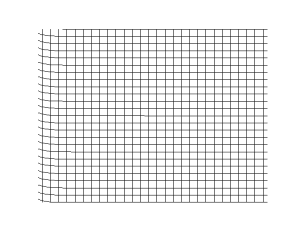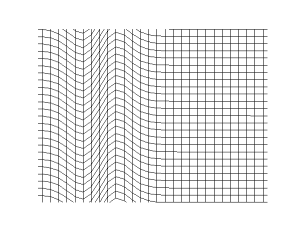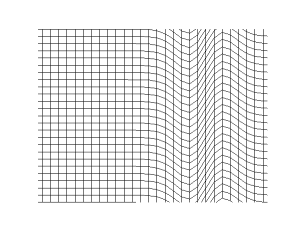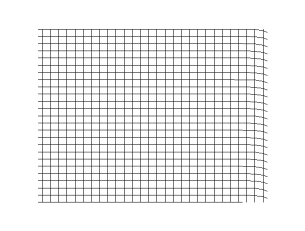
TRANSVERSE WAVES
TRANSVERSE WAVES: TIME DEPENDENCE
TIME DEPENDENCE
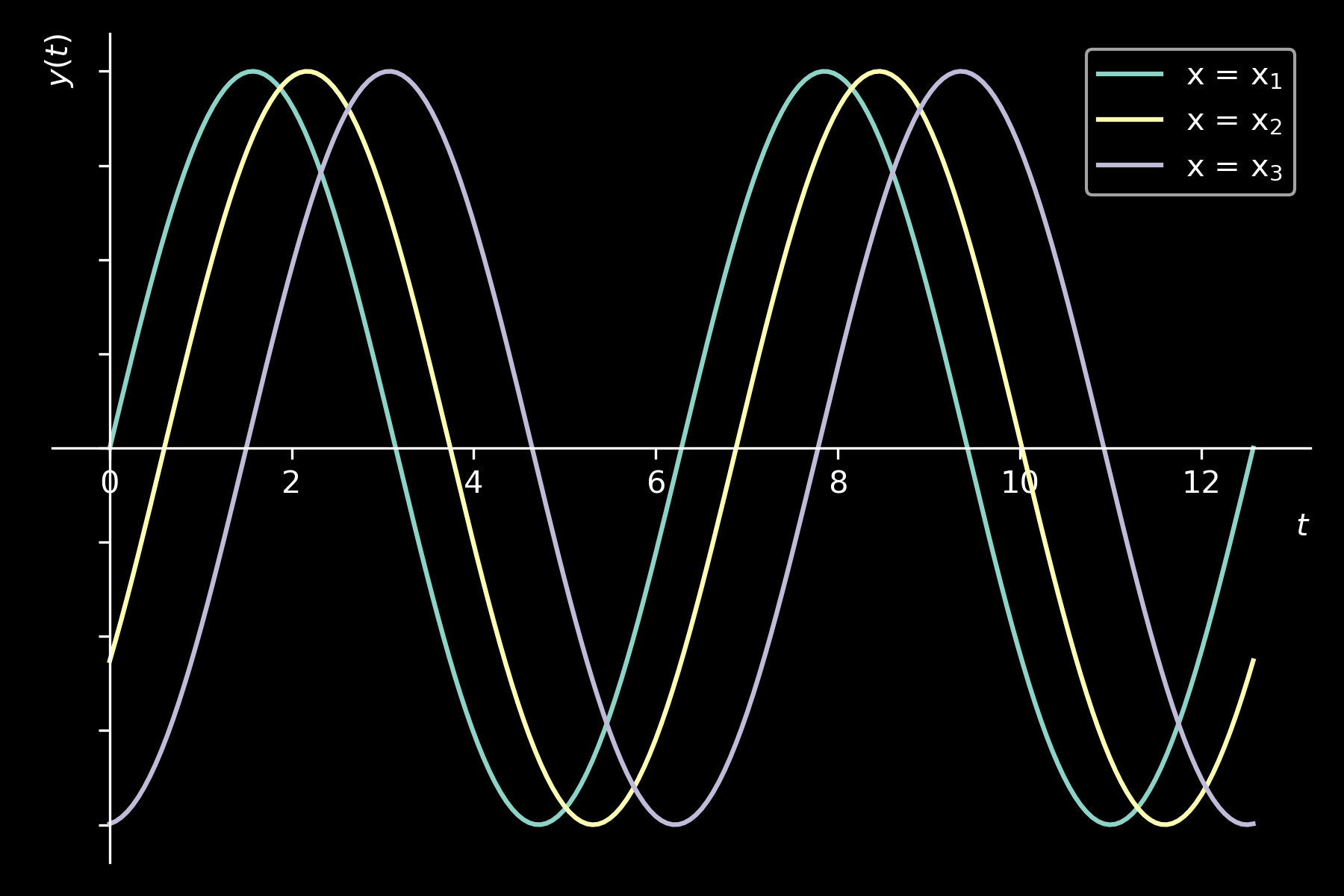
\( y(t) = y_{m} sin(\omega t + \phi_{x})\)
\( \omega=2 \pi \nu=\frac{2 \pi}{T} \)
\( \omega = angular \, frequency\)
\( T = period \)
\( \phi_{x} = spatial \, phase \)
TRANSVERSE WAVES: SPATIAL DEPENCENCE
SPATIAL DEPENDENCE
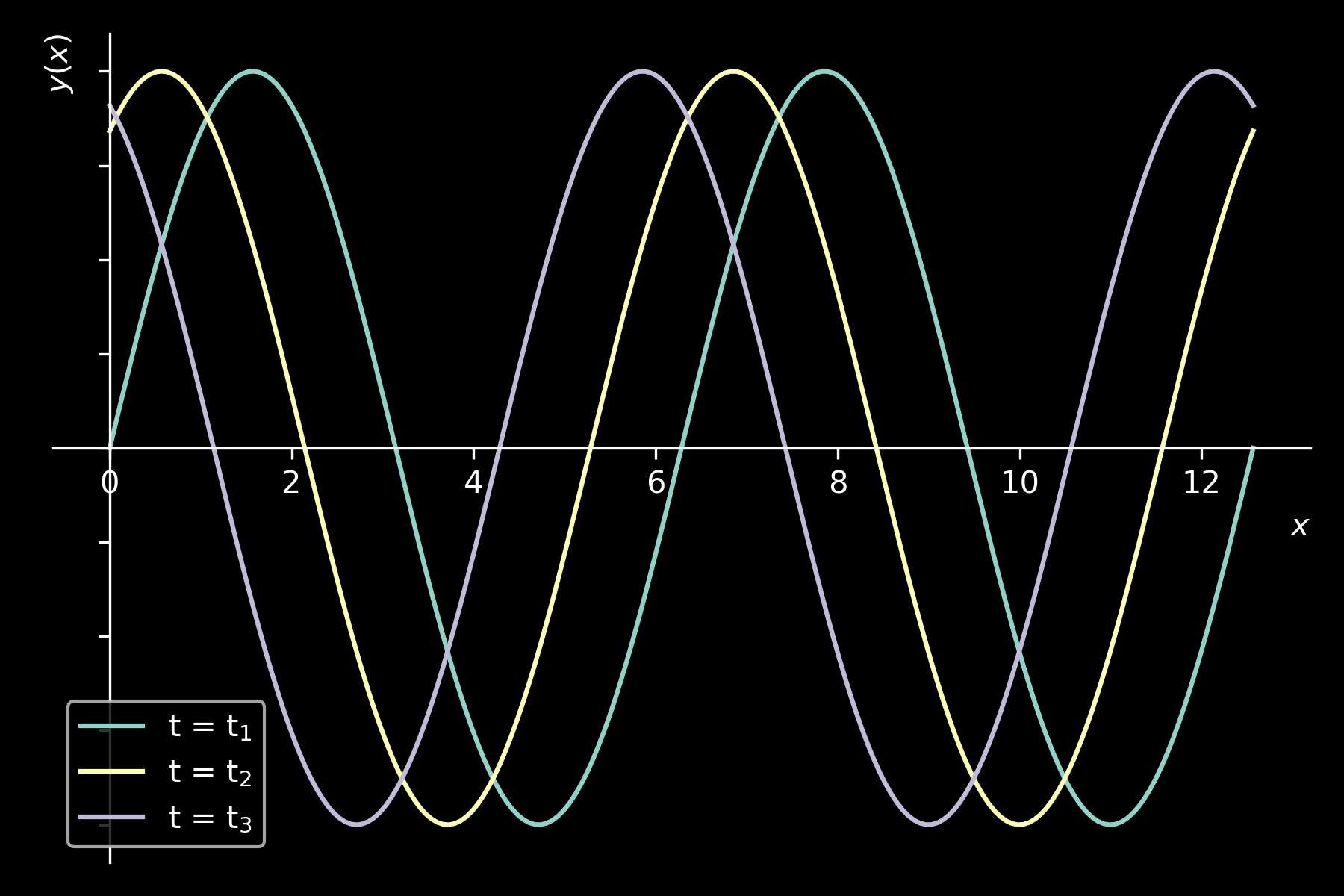
\( y(x) = y_{m} sin(k x + \phi_{t})\)
\( k = \frac{2 \pi}{\lambda}\)
\( k = wavenumber \)
\( \lambda = wavelength \, (spatial \, period) \)
\( \phi_{t} = temporal \, phase \)
TRANSVERSE SINUSOIDAL WAVE
\[ \phi_{x} = k x \]
\[ \phi_{t} = - \omega t \]
\[ y(x,t) = y_{m} sin (k x - \omega t + \phi) \]
\[ \phi = additional \, phase \]
PHASE SPEED OF A WAVE
\( k x - \omega t = \frac{\pi}{2} \)
\( x(t) = \frac{\pi}{2 k} + \frac{\omega}{k} t \)
\( x(t) = \frac{\lambda}{4} + \frac{\omega}{k} t = x_{0} + v_{phase} t \)
\( x_{0} = \frac{\lambda}{4}; \)
\[ \boxed{v_{phase} = \frac{\omega}{k} = \lambda \, \nu} \]
\[ \boxed{\omega =c \, k, \; c=\lambda \, \nu} \]
For Light
SUPERPOSITION PRINCIPLE FOR WAVES
"If two functions are a solution of the wave equations, then their sum is a valid solution"
\[ y_{1}(x,t); \; y_{2}(x,t) \Rightarrow y_{1}(x,t) + y_{2}(x,t) \]
\[ \frac{\partial^{2}[y(x,t)]}{\partial t^{2}} = v^{2}_{phase} \frac{\partial ^{2}[y(x,t)]}{\partial x^{2}} \]
INTERFERENCE BETWEEN SINUSOIDAL WAVES
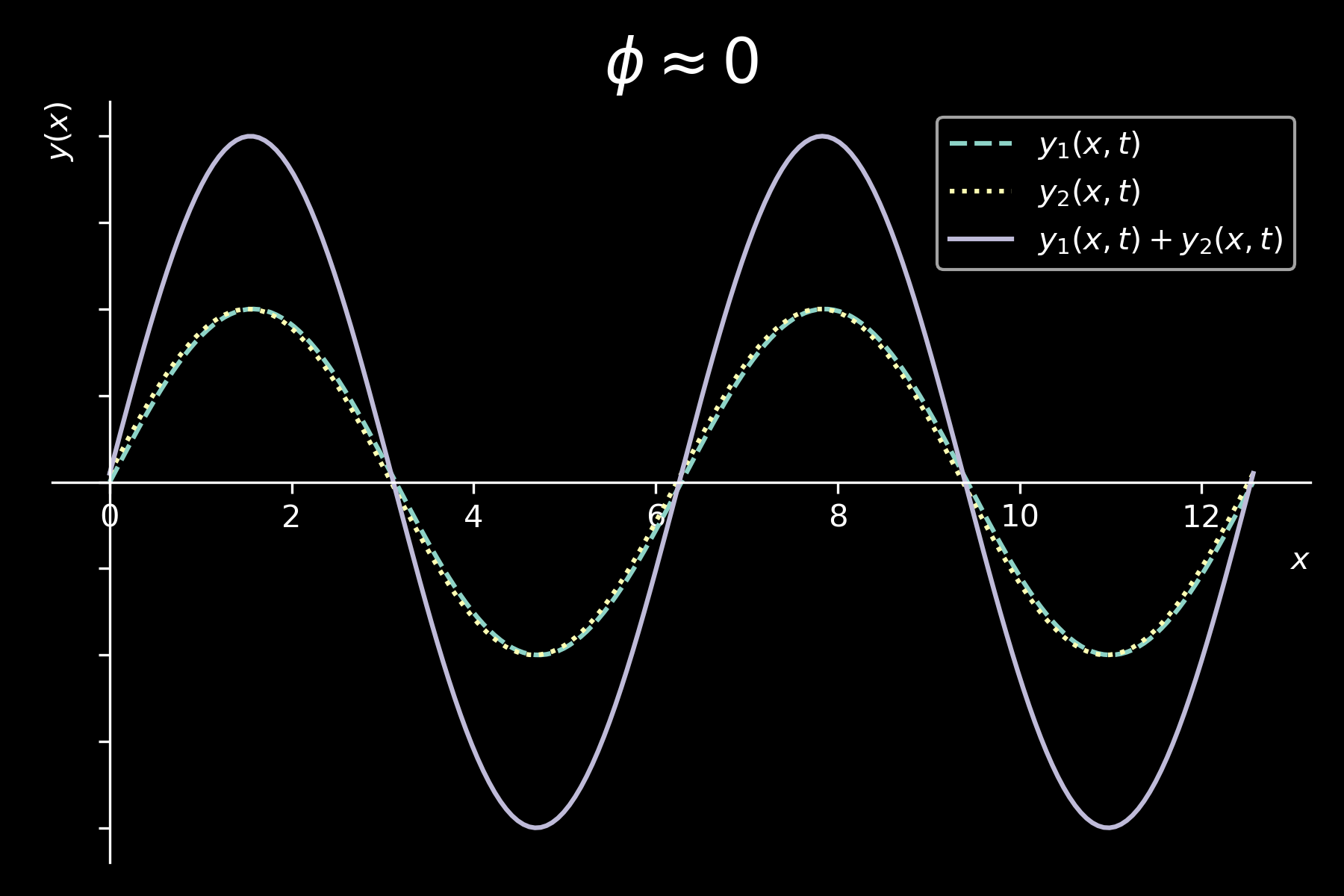
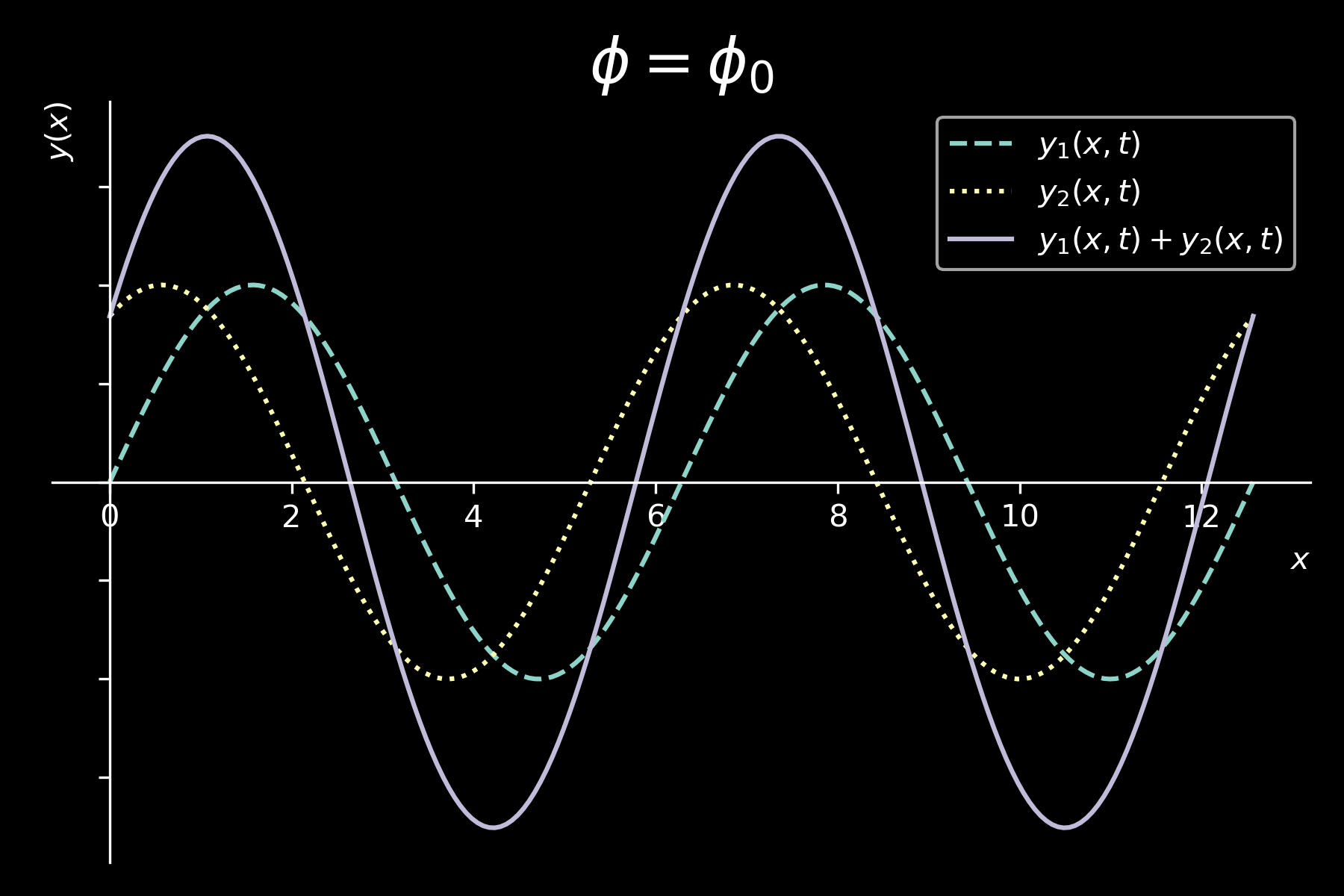
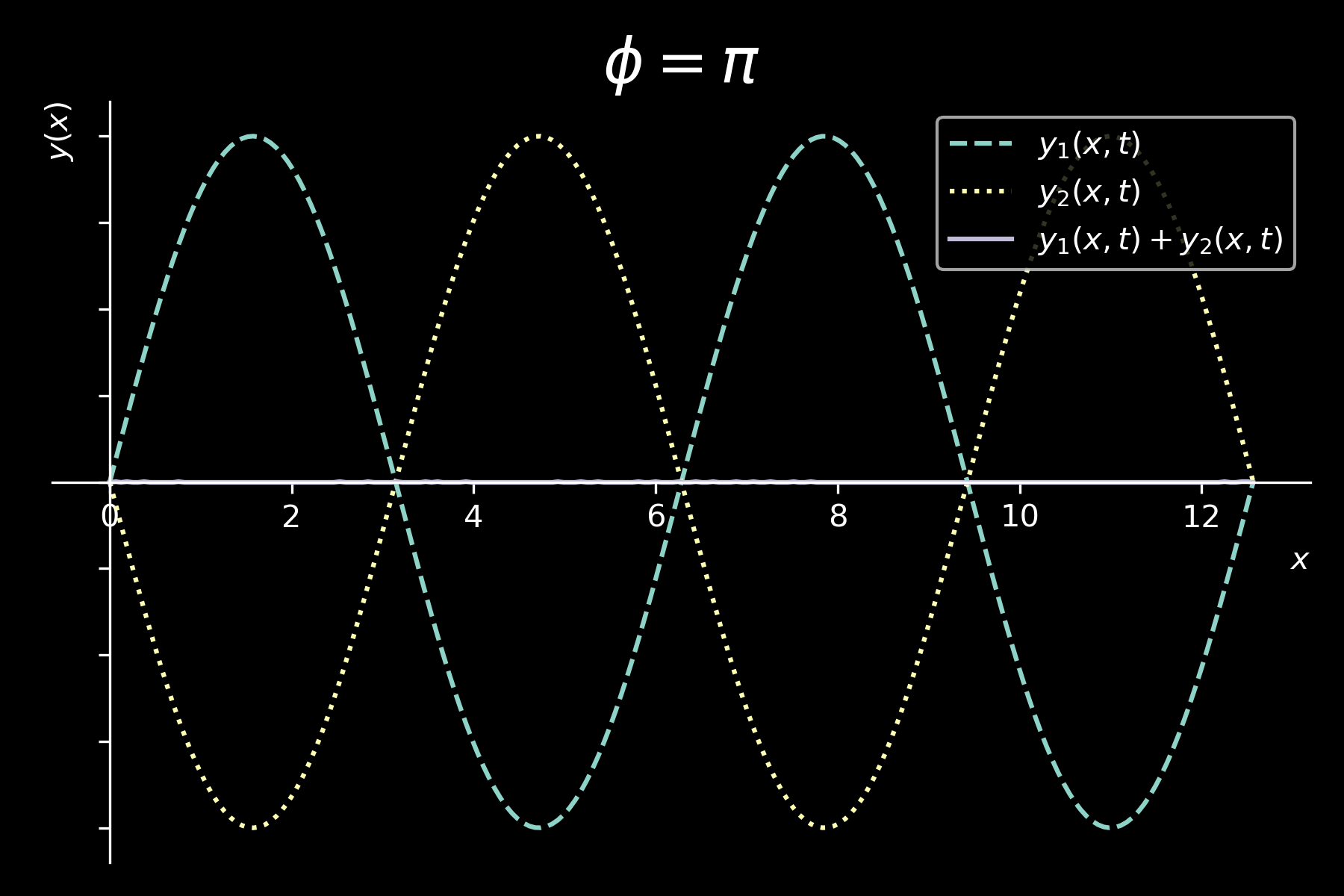
\( y_{1}(x,t) = y_{m} sin(kx - \omega t) \)
\( y_{2}(x,t) = y_{m} sin(kx - \omega t + \phi) \)
\[ \boxed{y(x,y) = y_{1}(x,t) + y_{2}(x,t) = 2 y_{m} cos \left( \frac{\phi}{2} \right) sin \left( kx - \omega t + \frac{\phi}{2} \right)} \]
INTERFERENCE, STATIONARY WAVES AND RESONANCES
\( y_{1}(x,t) = y_{m} sin(kx - \omega t) \)
\( y_{2}(x,t) = y_{m} sin(kx + \omega t) \)\( y(x,t) = y_{1}(x,t) + y_{2}(x,t) \)
\( \Downarrow \)
\[ \boxed{y(x,t) = [ 2 y_{m} sin(kx) ] cos( \omega t)} \]
\[ \boxed{ \lambda = \frac{2 L}{n}; \; n=1,2,3...} \]
INTERFERENCE, STATIONARY WAVES AND RESONANCES
WAVES: COMPLEX FORMALISM AND PLANE WAVES
\( y(x,t) = y_{m} cos(kx - \omega t + \phi) \)
\( \omega=2 \pi \nu=\frac{2 \pi}{T}\)
\( k = \frac{2 \pi}{\lambda}\)
\tilde{y}(x,t) = y_{m} cos(kx - \omega t + \phi) + i \, y_{m} sin(kx - \omega t + \phi)
e^{i \, \alpha} = cos(\alpha) + i \, sin(\alpha)
\tilde{y}(x,t) = \tilde{y}_{m} e^{i(kx - \omega t)}; \; \tilde{y}_{m}=y_{m} e^{i \phi}
\tilde{y}(x,t) = y_{m} e^{i(kx - \omega t + \phi)} = y_{m} e^{i \phi} e^{i(kx - \omega t)}
f(x)
is a well behaved function
\hat{f}(k) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} f(x) e^{-ikx}
is its Fourier transform
f(x) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} \hat{f}(k) e^{ikx}
is its inverse Fourier transform
k=\frac{2 \pi}{\lambda}
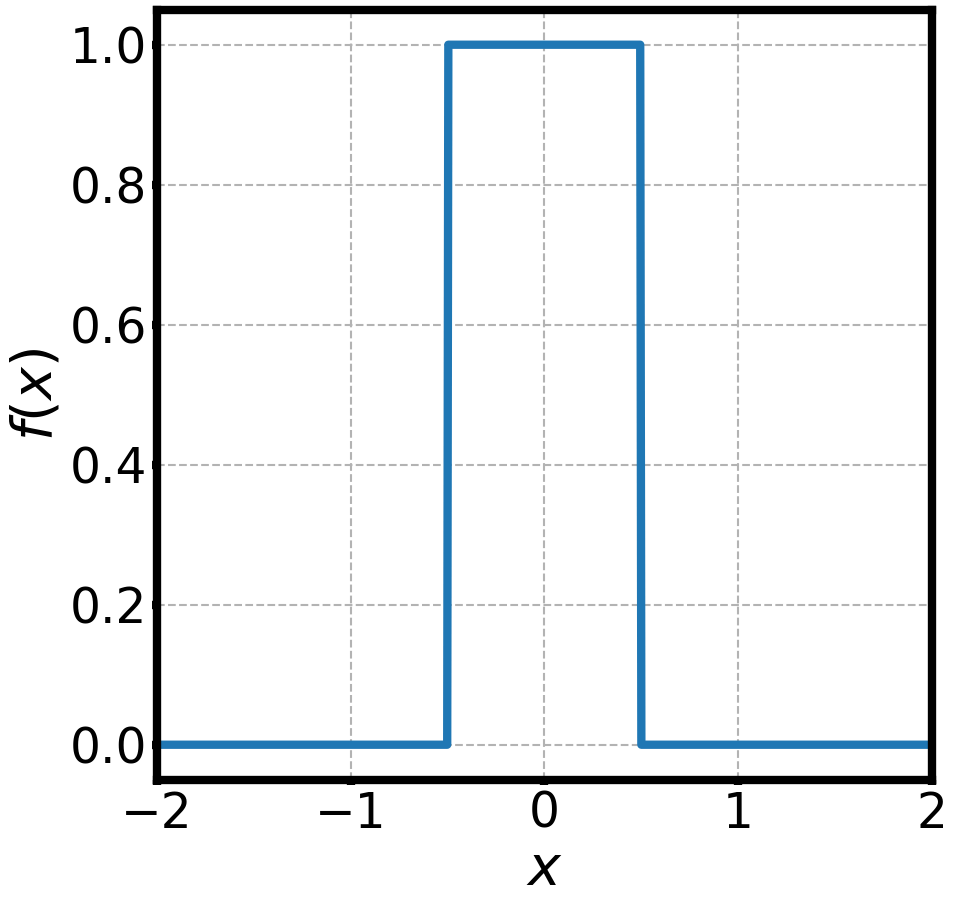
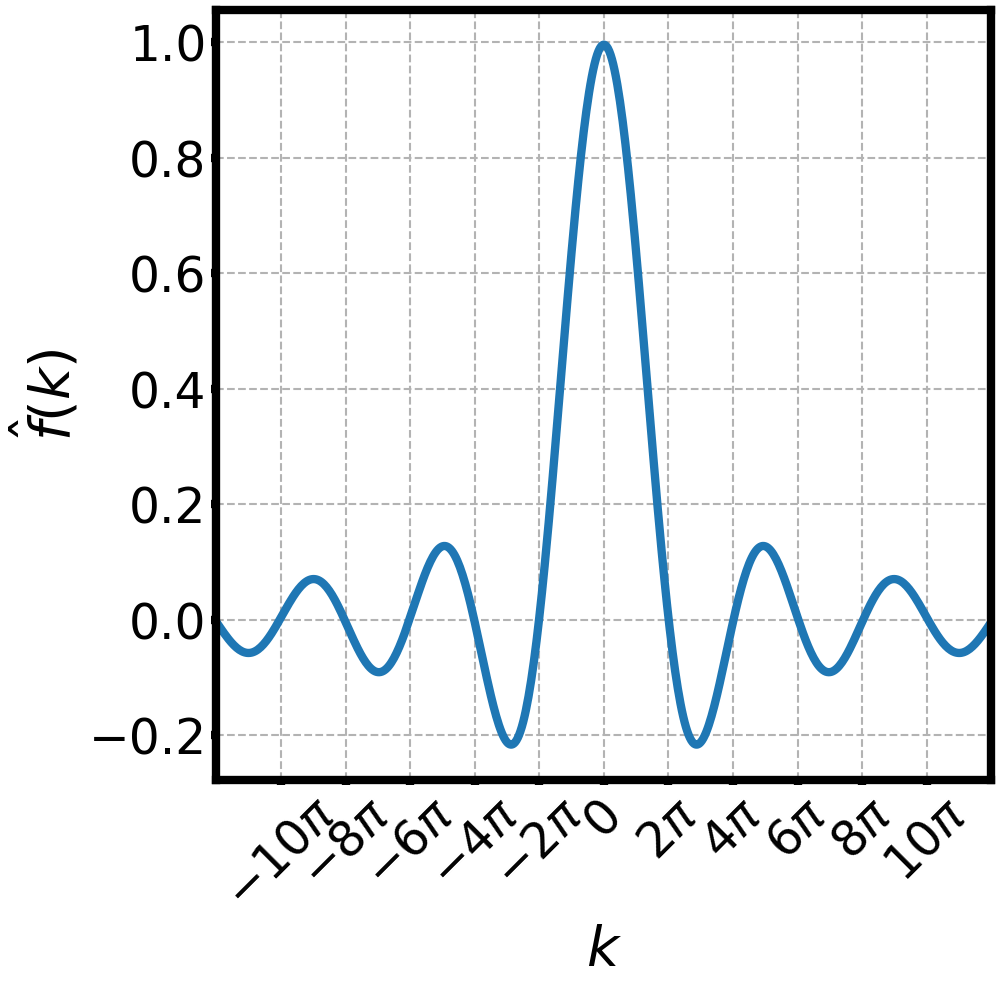
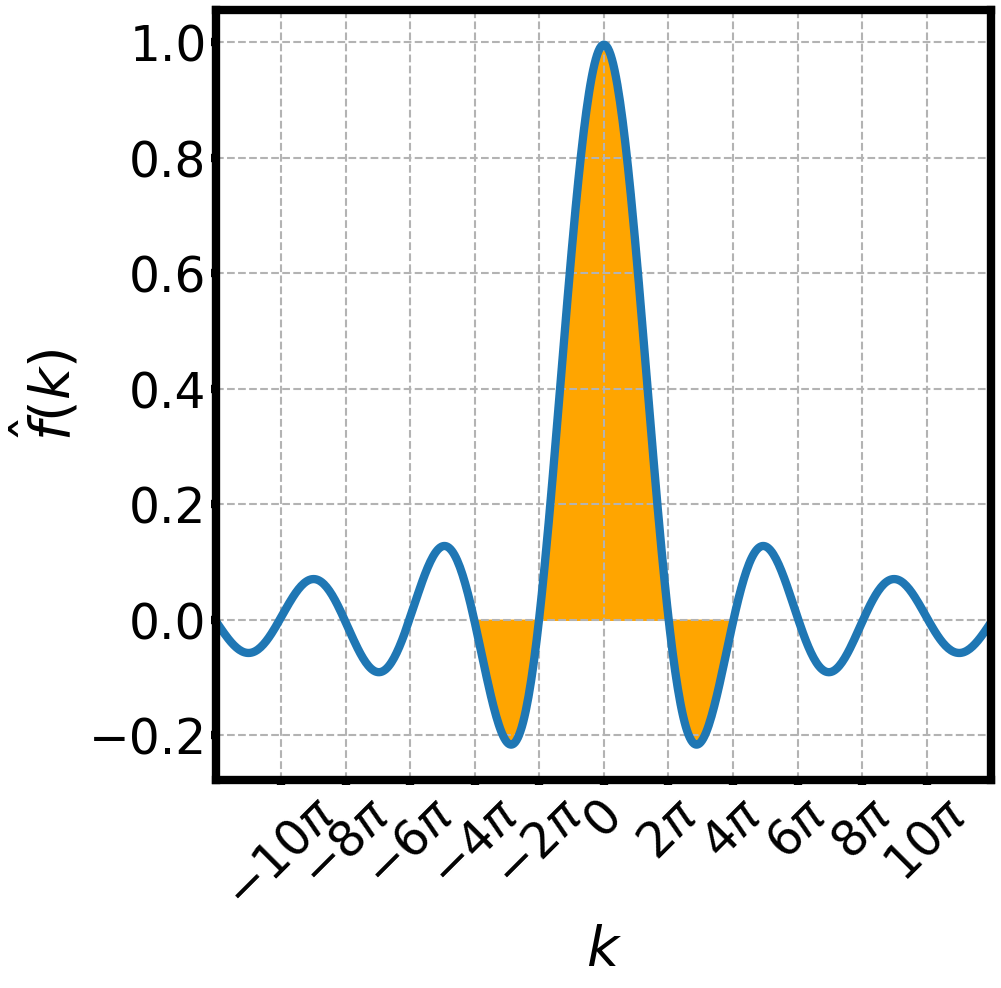
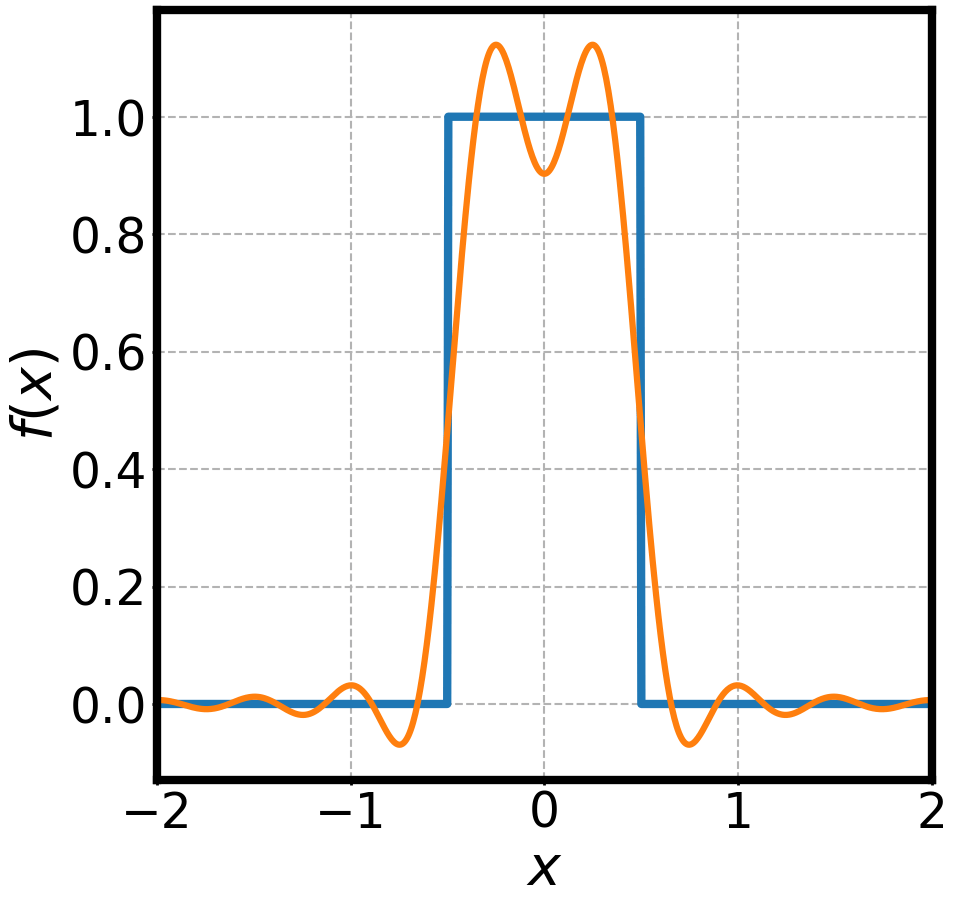
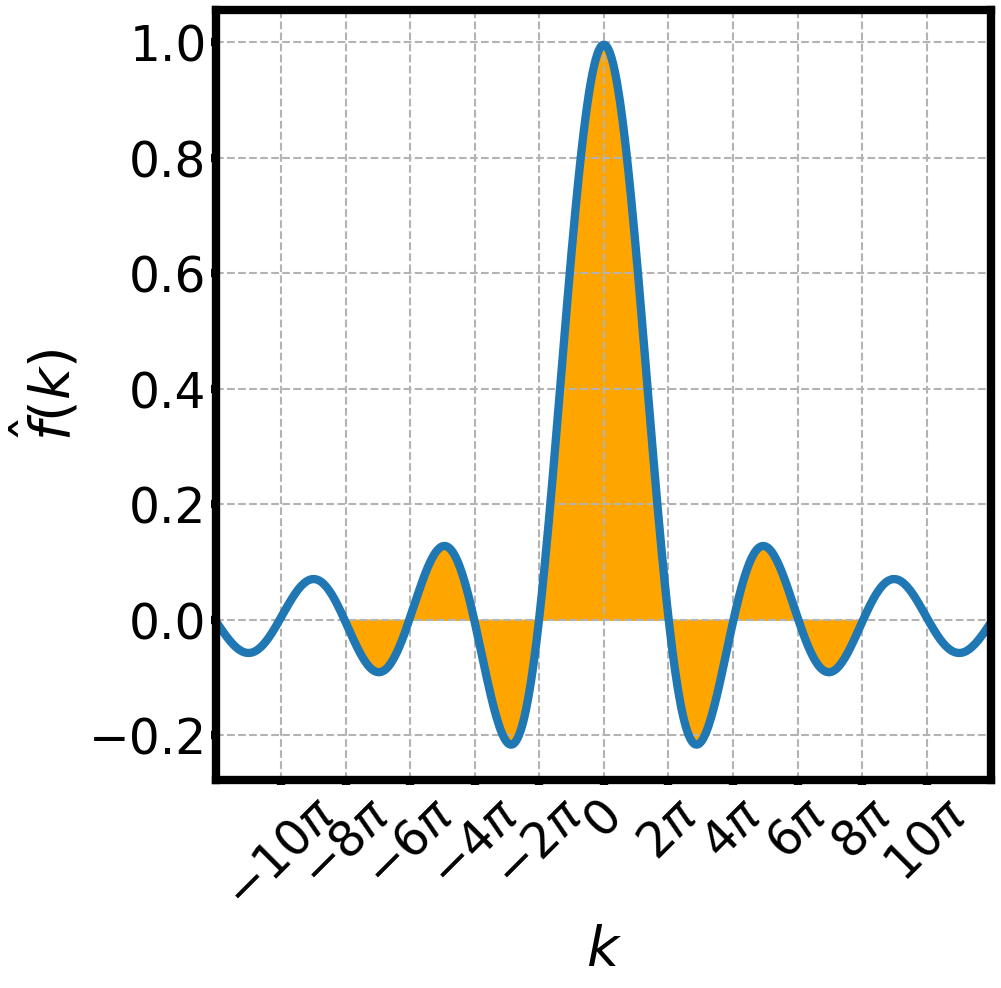
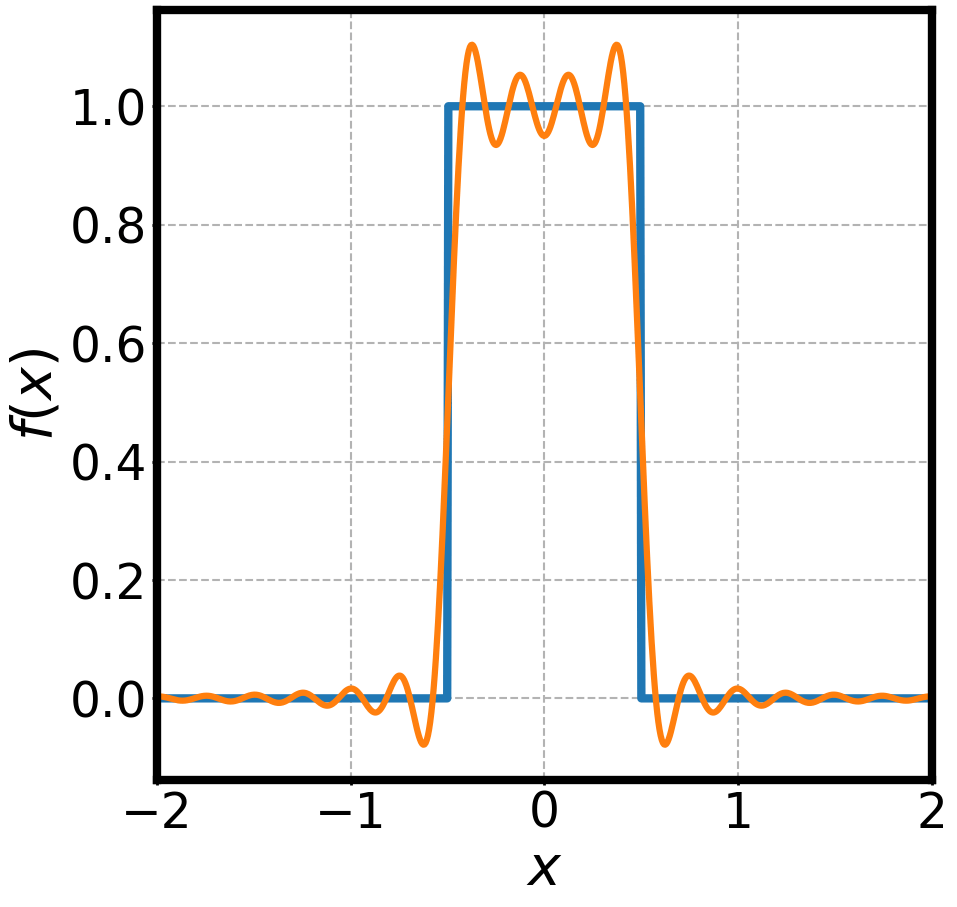
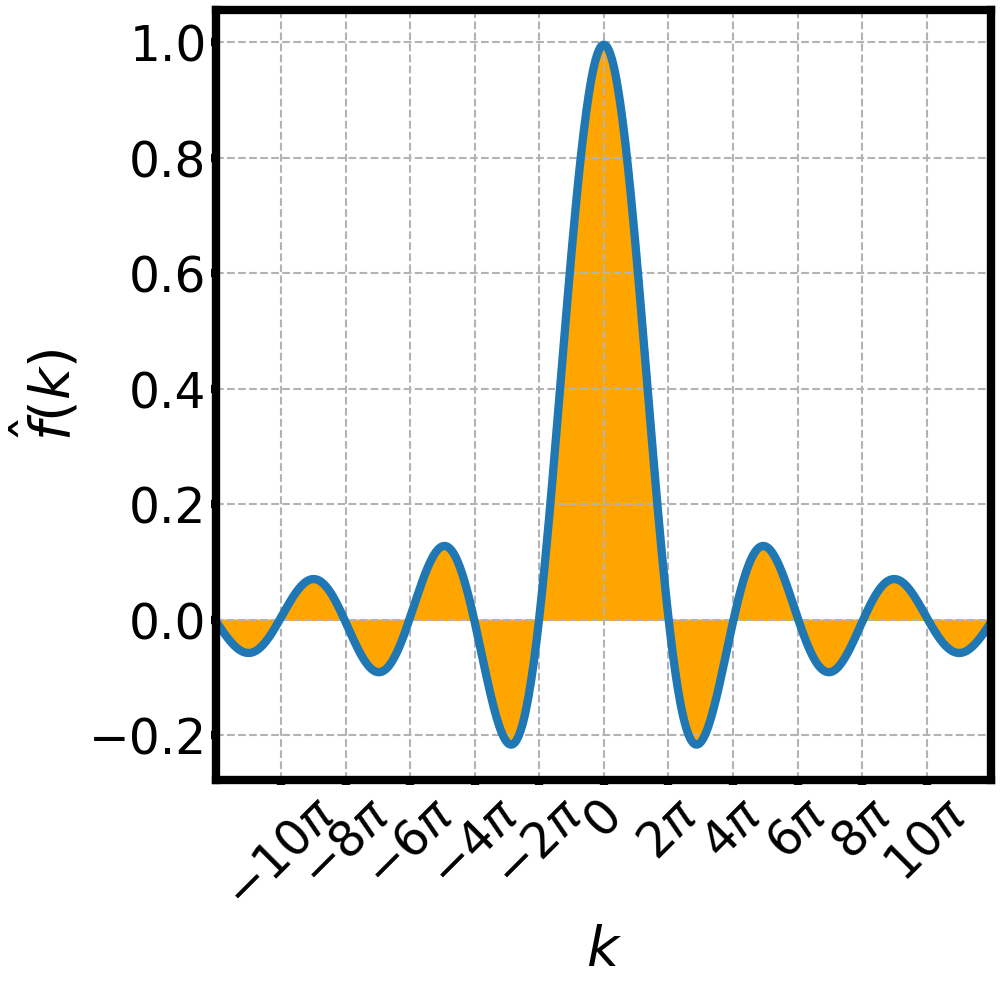
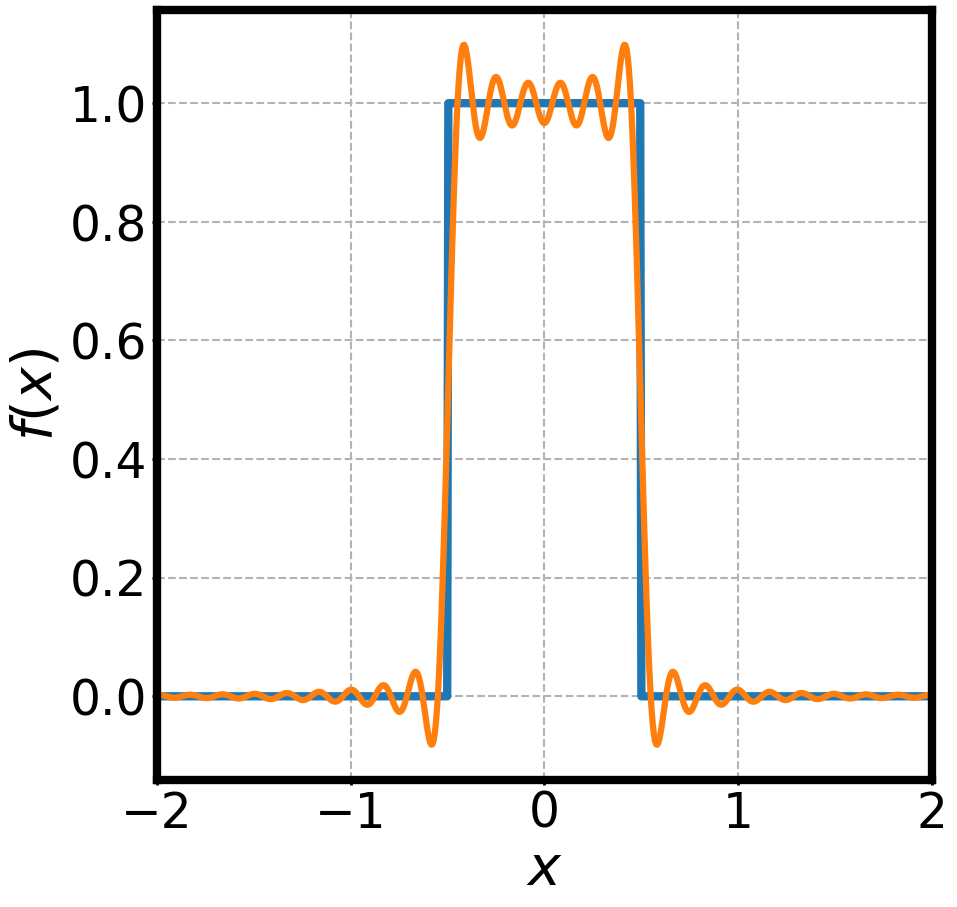
WAVES AND FOURIER TRANSFORMS
WAVES AND FOURIER TRANSFORMS
f(x)
is a well behaved function
\hat{f}(k) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} f(x) e^{-ikx}
is its Fourier transform
f(x) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} \hat{f}(k) e^{ikx}
is its inverse Fourier transform
k=\frac{2 \pi}{\lambda}
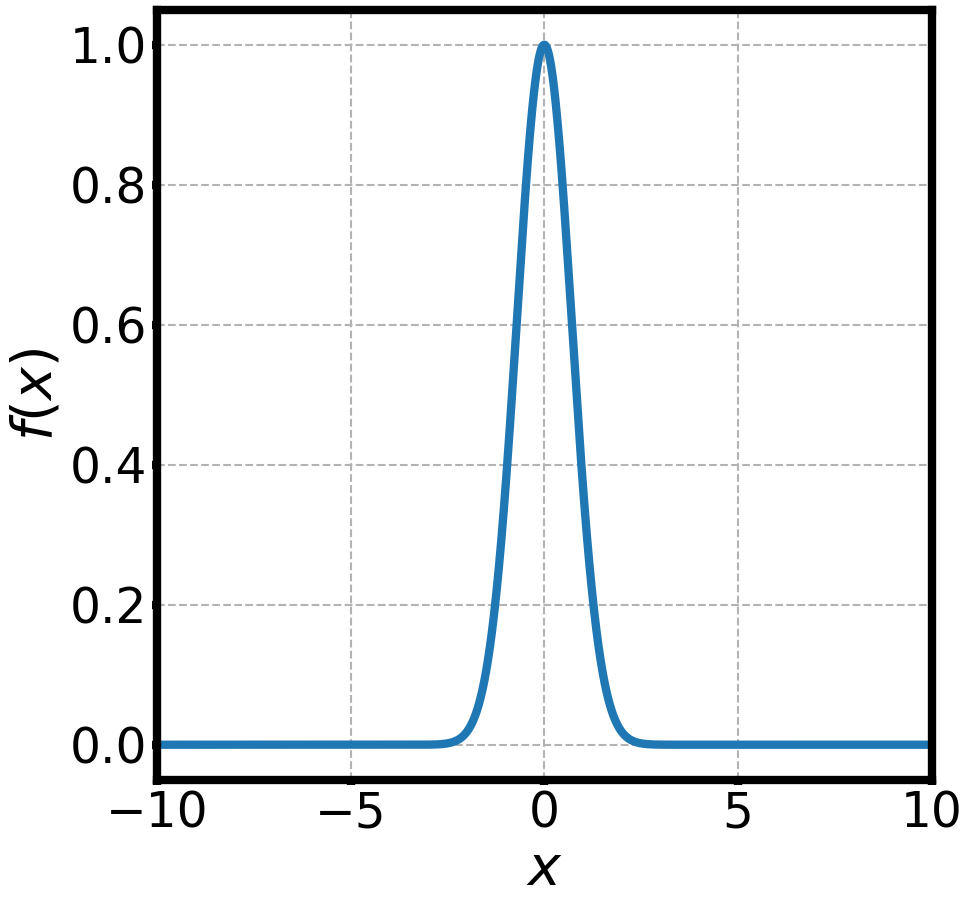
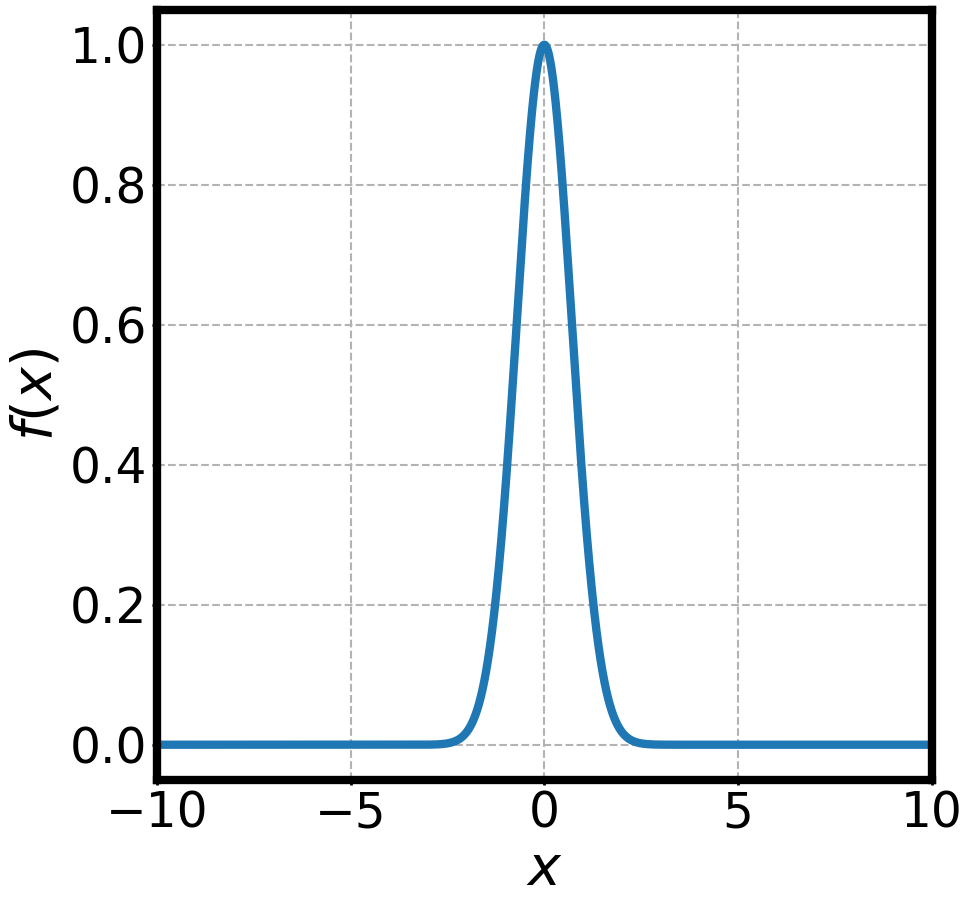
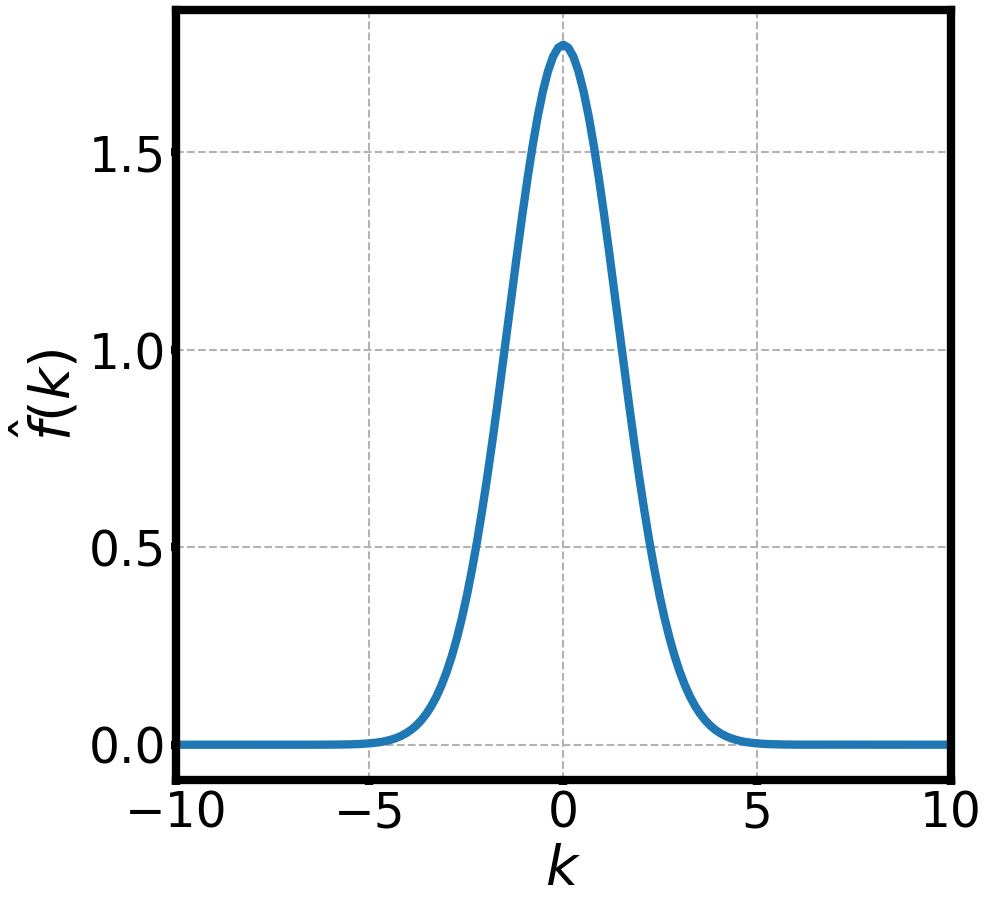
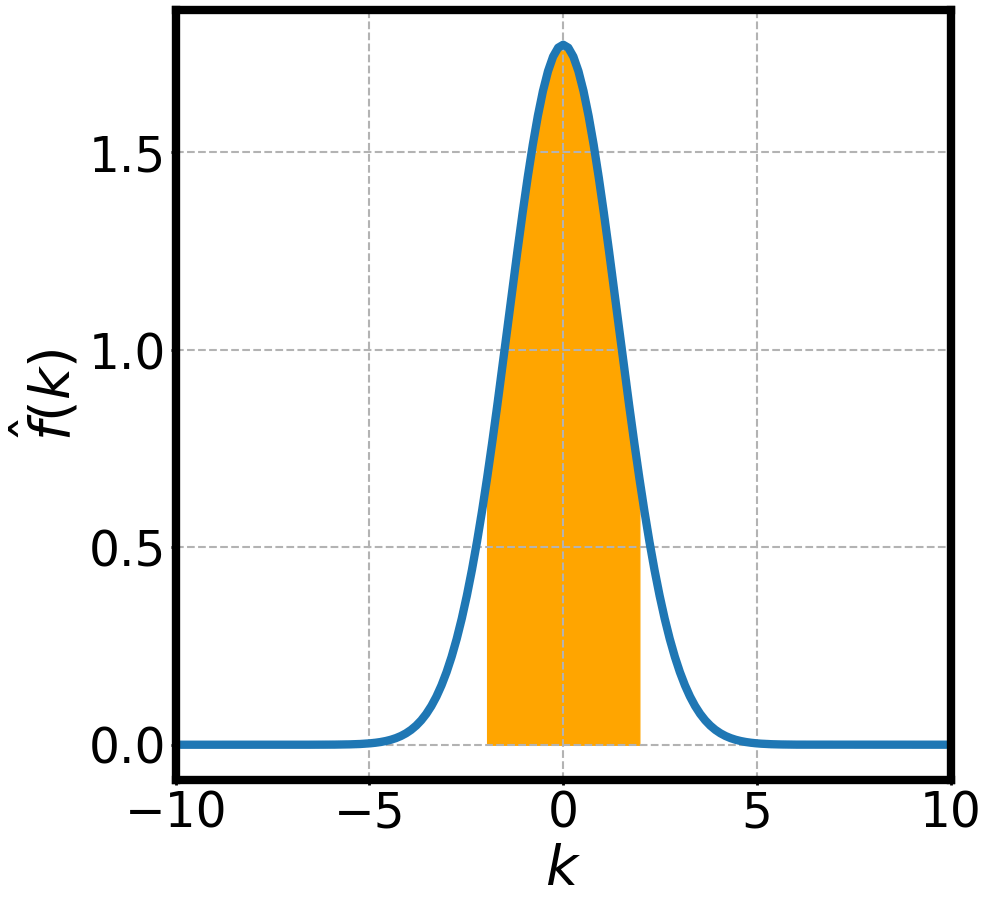
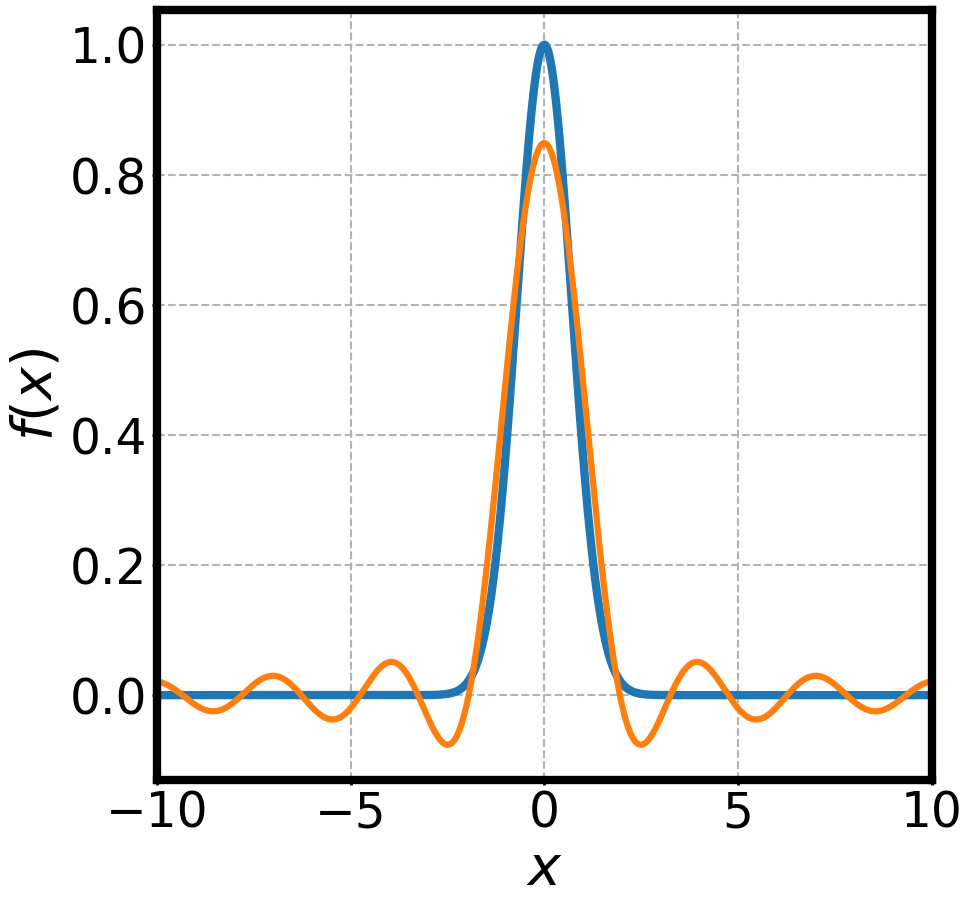
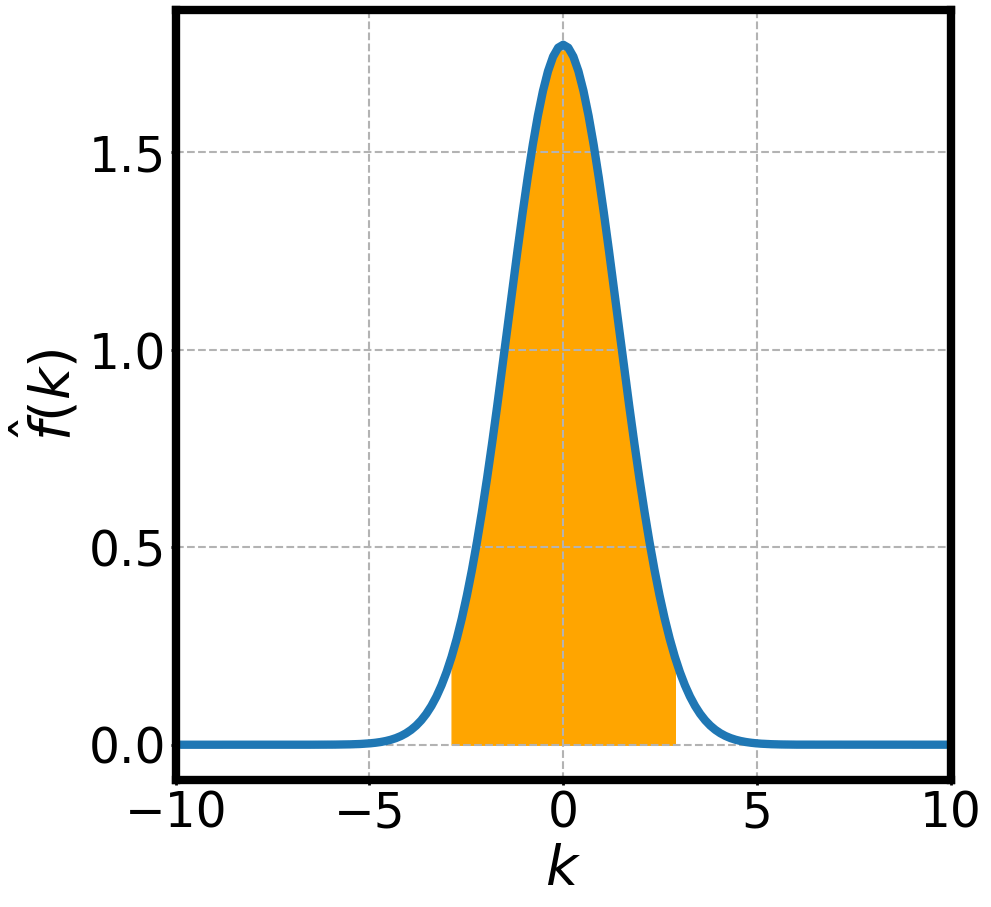
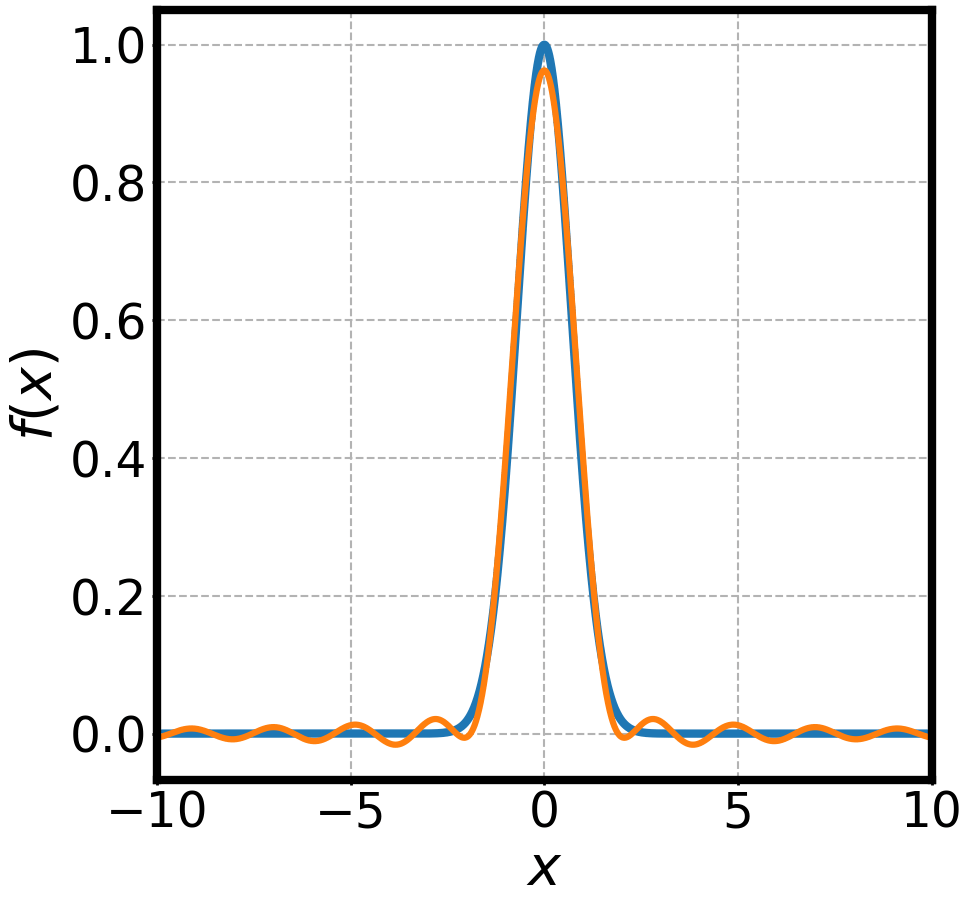
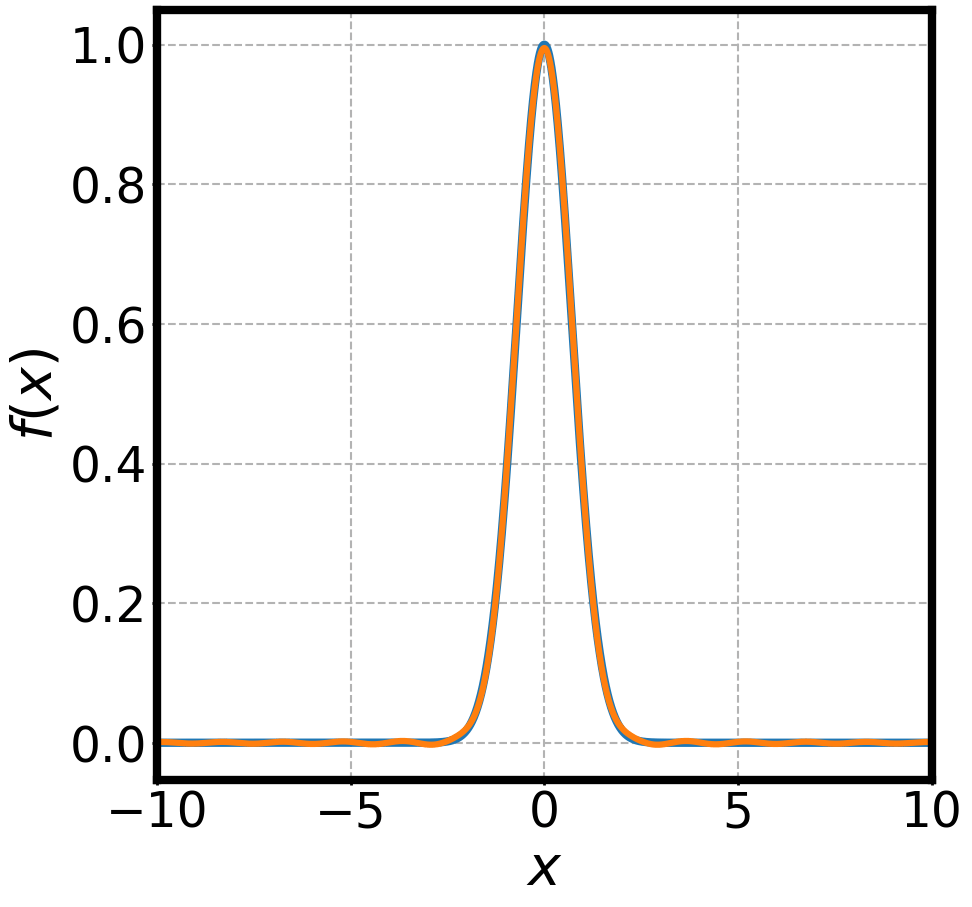
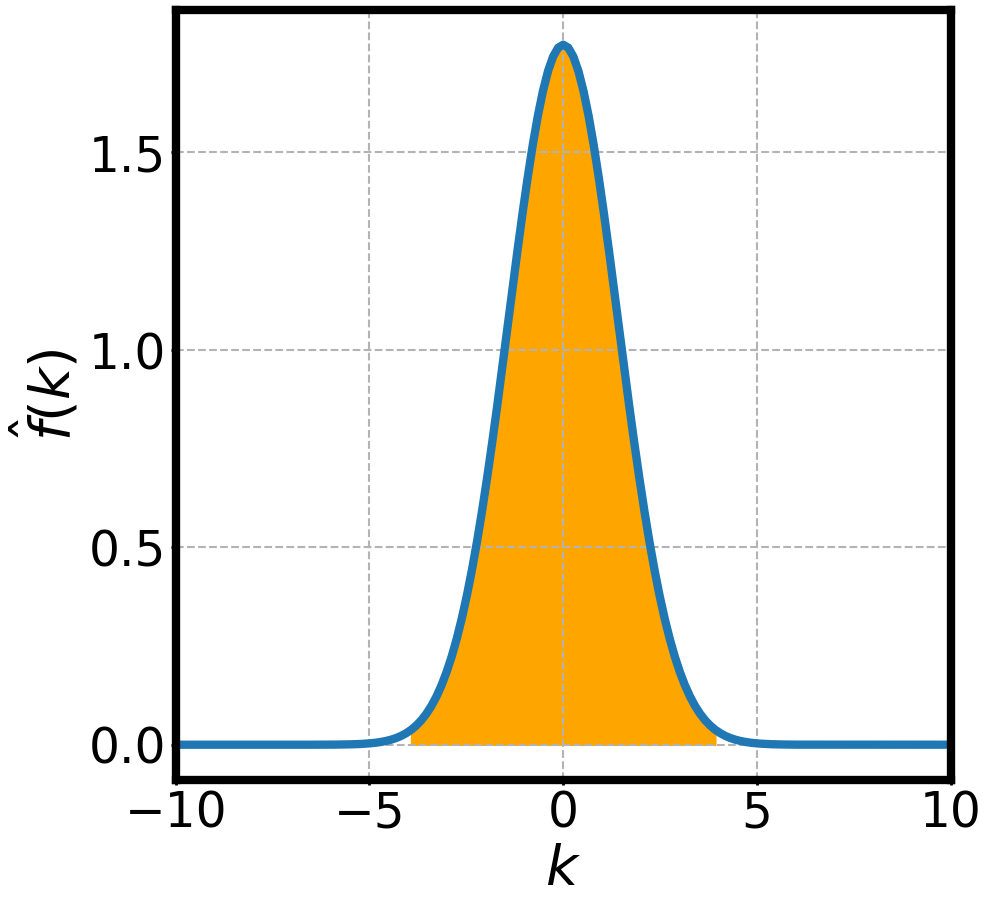
NON-DISPERSIVE WAVES PACKETS AND FOURIER TRANSFORMS
\hat{f}(k) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} f(x,0) e^{-ikx}
f(x,t) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} \hat{f}(k) e^{i(kx-\omega (k)t)}
v_g = \frac{d \omega (k)}{dk}
Group Velocity
NON-DISPERSIVE WAVES PACKETS AND FOURIER TRANSFORMS
v_{p} < v_{g}
v_{p} = v_{g}
v_{p} > v_{g}
DISPERSIVE WAVES PACKETS
\omega (k) = \frac{\hbar k^2}{2m}
v_{g} = \frac{\omega (k)}{dk}\bigg\rvert_{k=k_{0}} = \frac{\hbar k_{0}}{m}
v_{p} = \frac{\omega (k)}{k} = \frac{\hbar k}{2m}
Materials and Platforms for AI - Wave Theory
By Giovanni Pellegrini
