Dinamica: le forze e i loro effetti
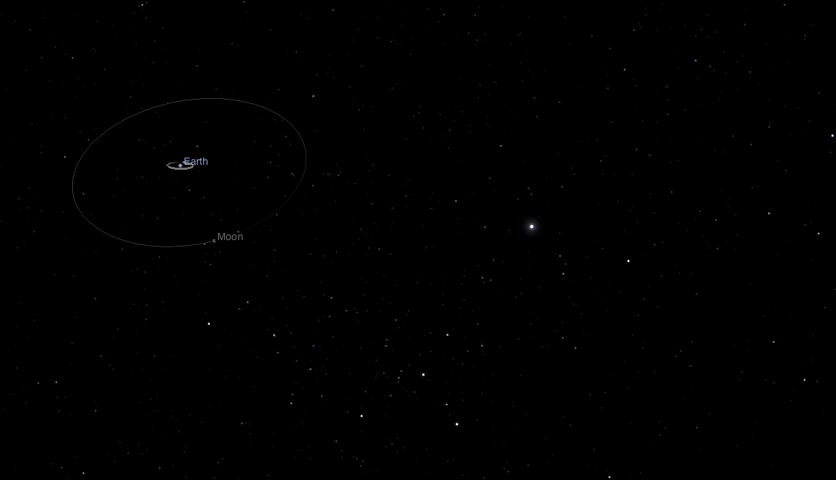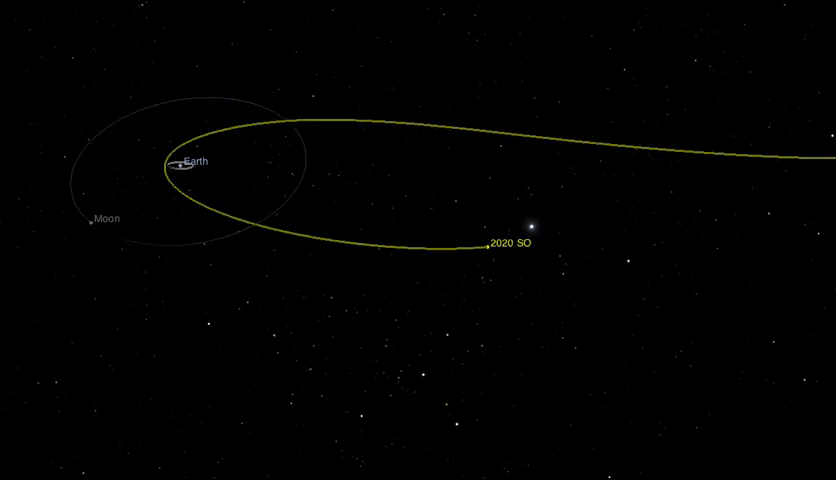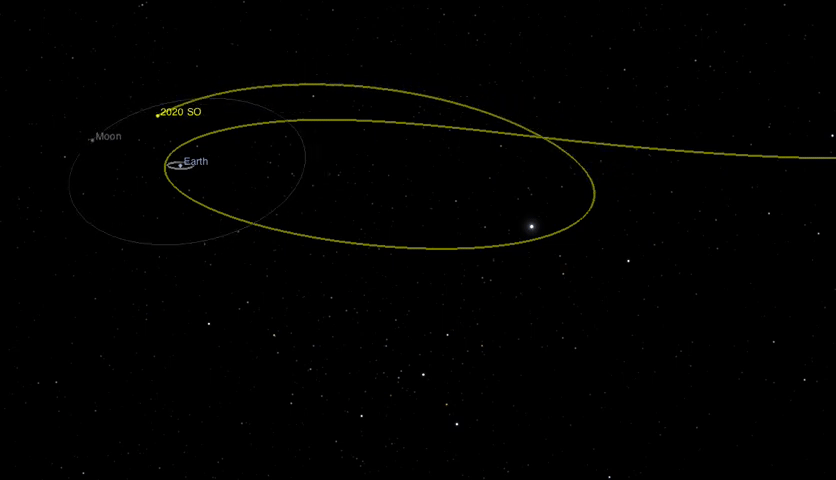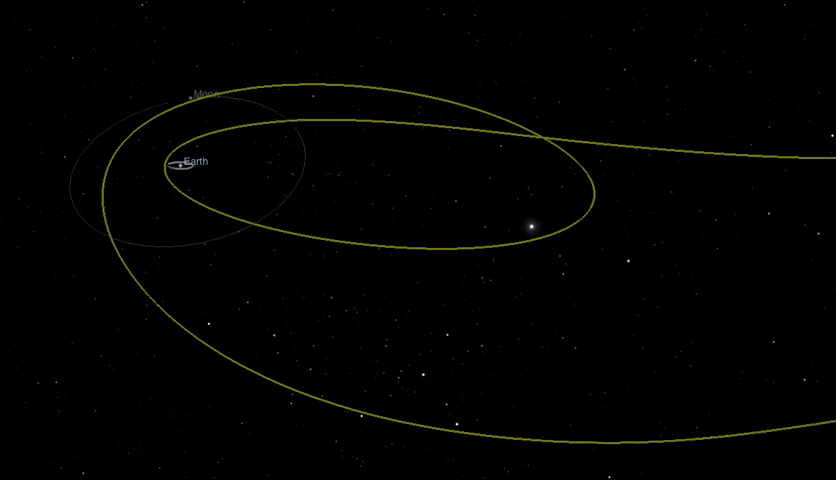
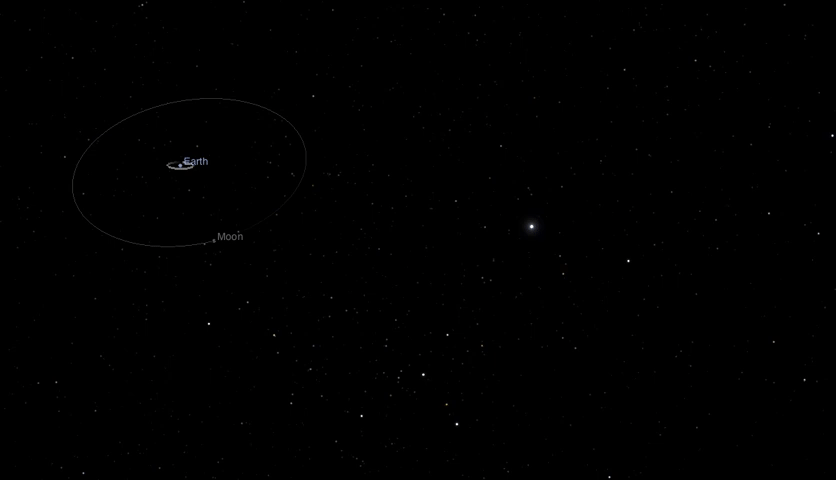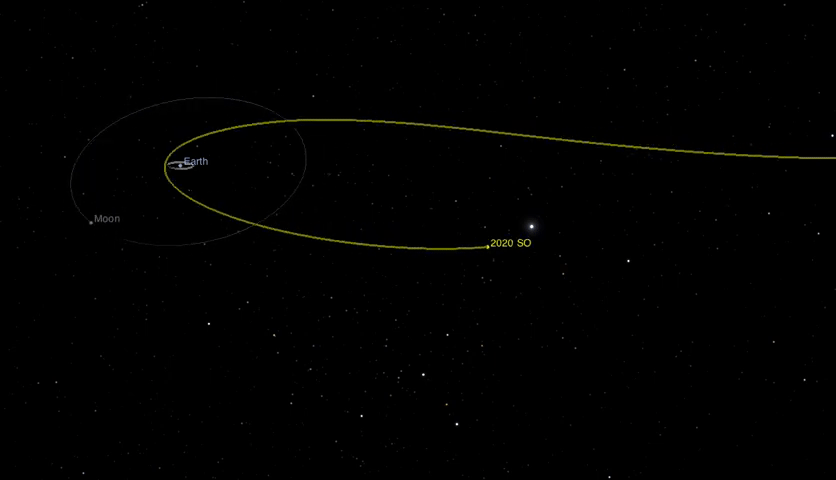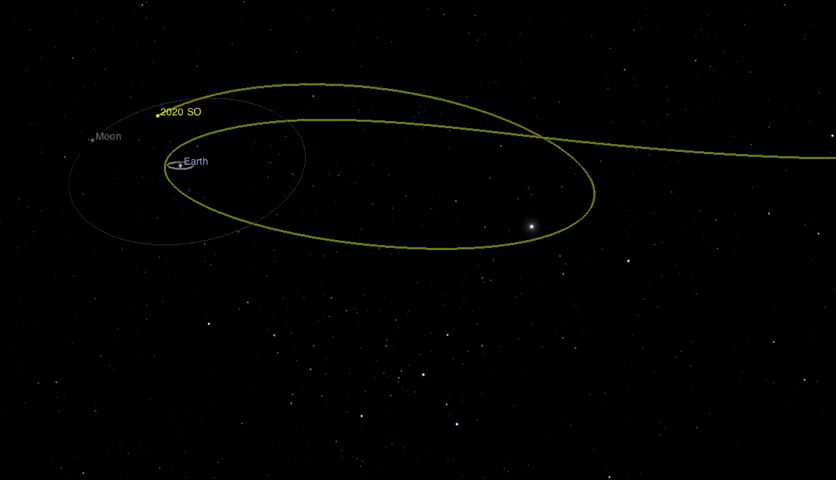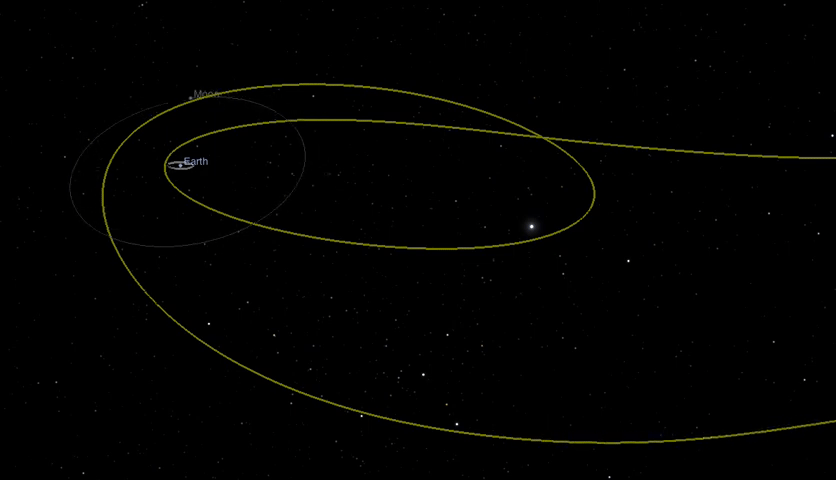
Dinamica: per muovere un oggetto...
- Occorre spingerlo o tirarlo
- Più forte è la spinta più rapido è lo spostamento
- Spinta e trazione possono essere in diverse direzioni
- Oggetti pesanti si spostano con più difficoltà

dinamica: formalizziamo l'intuizione
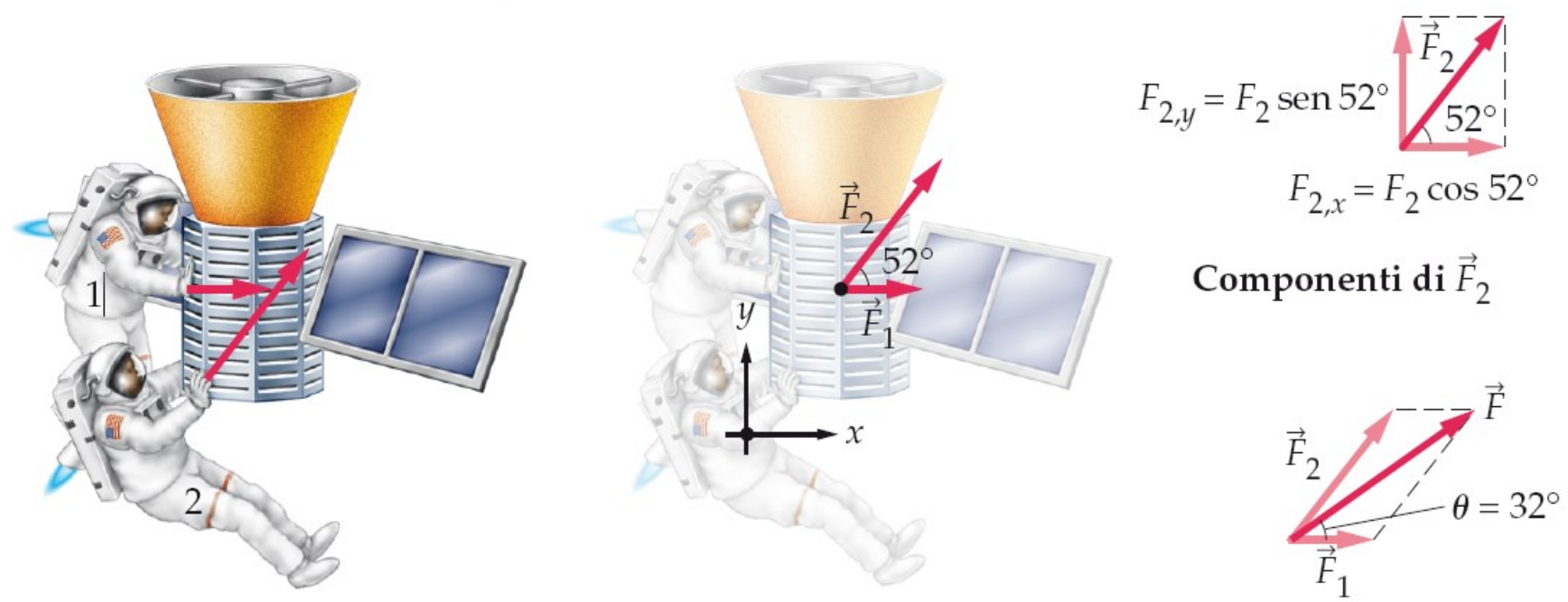
Spingere un oggetto ➡️ Esercitare una forza
La spinta ha intensità, direzione e verso ➡️ La forza è un vettore
Oggetti pesanti si spostano con più difficoltà ➡️ Massa inerziale: difficoltà nel cambiare velocità
prima legge di newton
principio d'inerzia
In assenza di forze esterne, un oggetto continuerà a muoversi di moto rettilineo uniforme, o resterà in quiete
si dice sistema di riferimento inerziale un sistema di riferimento in cui la prima legge di newton è valida.
sistemi di riferimento non inerziali: TRaslazioni
si dice sistema di riferimento non inerziale un sistema di riferimento in cui la prima legge di newton non è valida.
sistemi di riferimento non inerziali: rotazioni
si dice sistema di riferimento non inerziale un sistema di riferimento in cui la prima legge di newton non è valida.
seconda legge di newton
forza e accelerazione sono grandezze vettoriali direttamente proporzionali. Il loro rapporto è la massa, costante dipendente dal corpo in esame.
\, \vec{F}=m\vec{a} \,
equazione fondamentale della dinamica
[\mathrm{Kg \cdot m \cdot s^{-2}}]
[N]
Risultante delle forze: somme vettoriali![risultante]()
\vec{F} = \sum_{i} \vec{F}_{i}
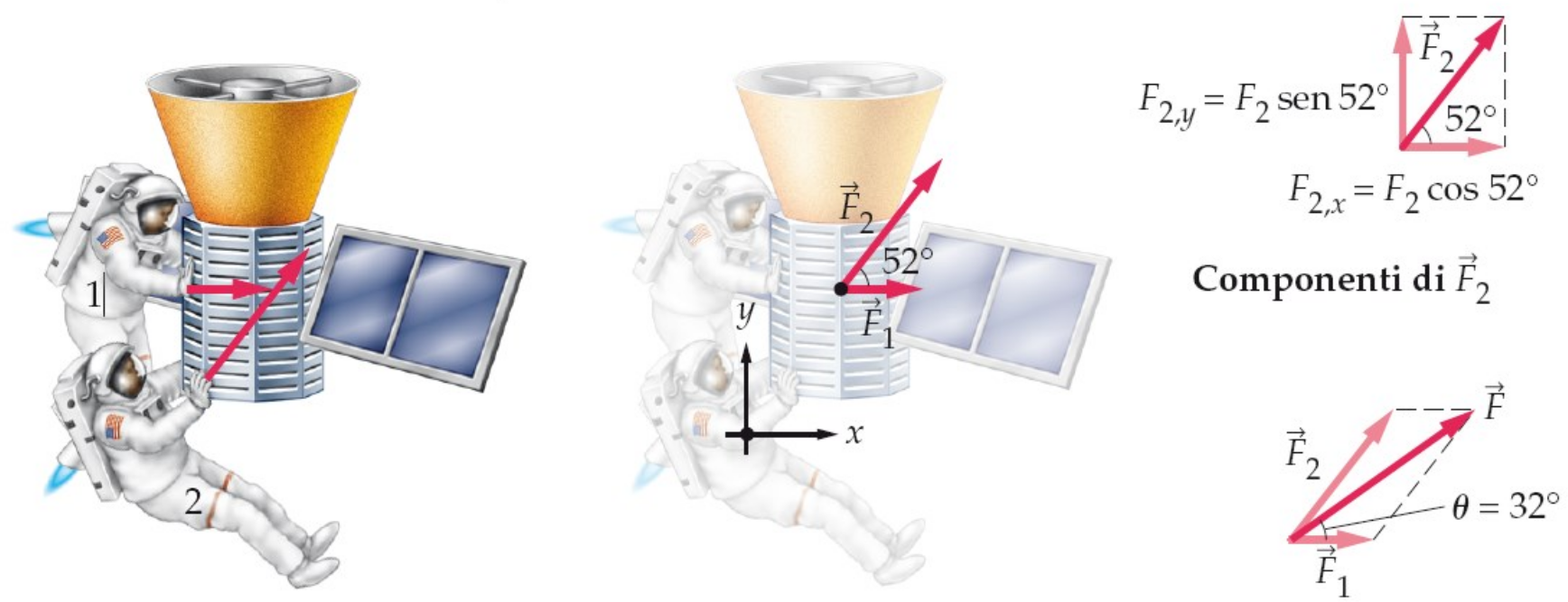
Rappresentazione delle forze
Diagramma di corpo libero
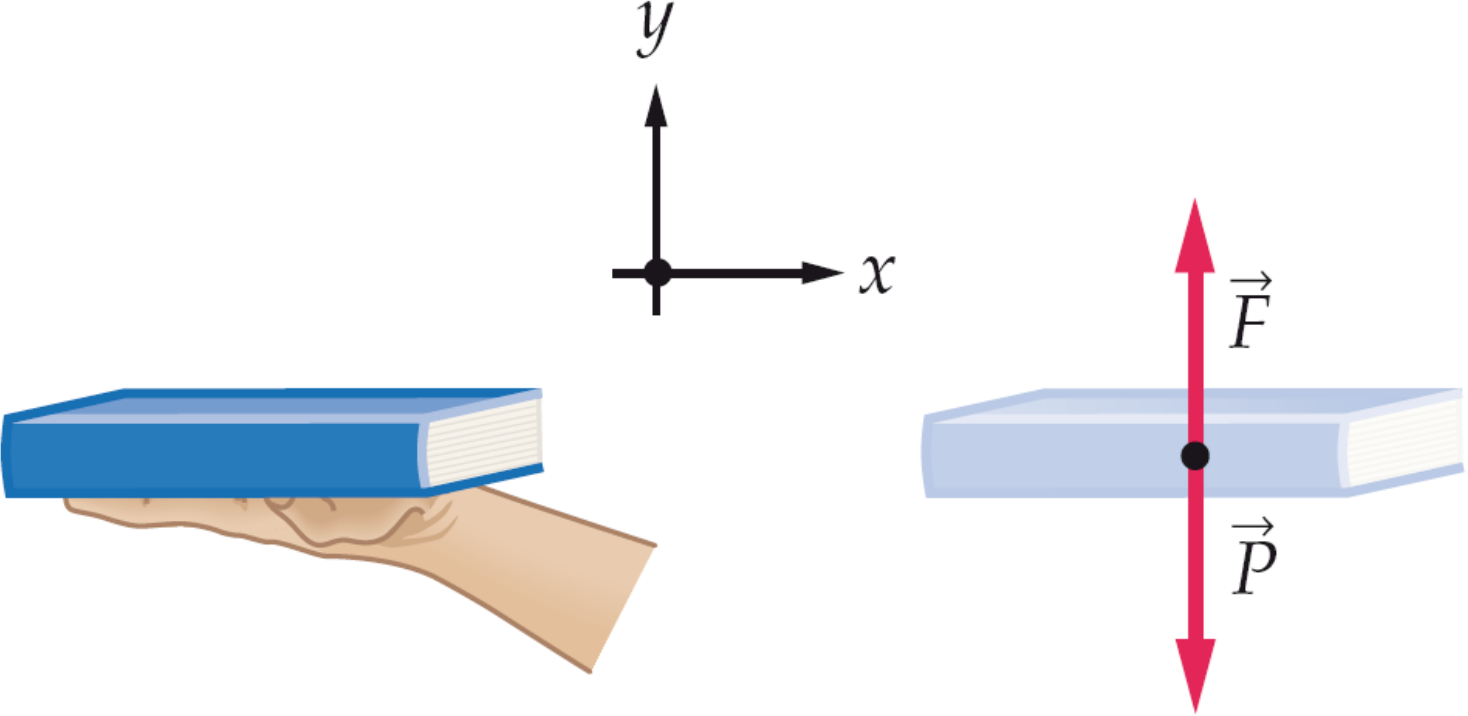
Terza legge di newton
Ad ogni azione corrisponde una reazione uguale e contraria: ossia le forze reciproche fra due corpi sono sempre uguali in module e dirette in versi opposti.
\, \vec{F_{12}}=-\vec{F_{21}} \,
principio di azione e reazione

Terza legge di newton
Love + death + robots: dare una mano
forze: forza gravitazionale
\, \vec{F} = -G \frac{m_{1}m_{2}}{r^{2}} \vec{u_{r}}
legge di gravitazione universale
G = 6.67 \cdot 10^{-11} [N \cdot m^{2} / Kg^{2}]
costante di gravitazione universale
r
\vec{u_{r}}
m_{1}
m_{2}
\vec{F}_{21}
\vec{F}_{12}
forze: forza peso
\, \vec{F} = -G \frac{m_{1}m_{2}}{r^{2}} \vec{u_{r}}
G = 6.67 \cdot 10^{-11} [N \cdot m^{2} / Kg^{2}]
\, M = 5.98 \cdot 10^{24} \, [Kg]
\, R = 6.38 \cdot 10^{6} \, [m]
\, \vec{g} = -G \frac{M}{R^{2}} \vec{u_{r}}
forze: reazione vincolare normale
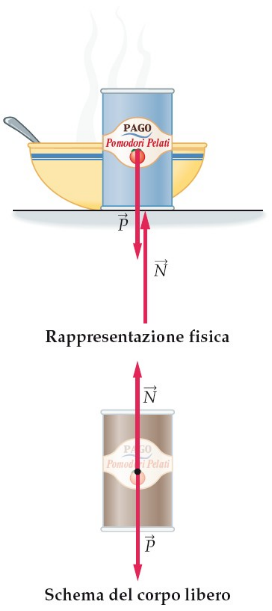
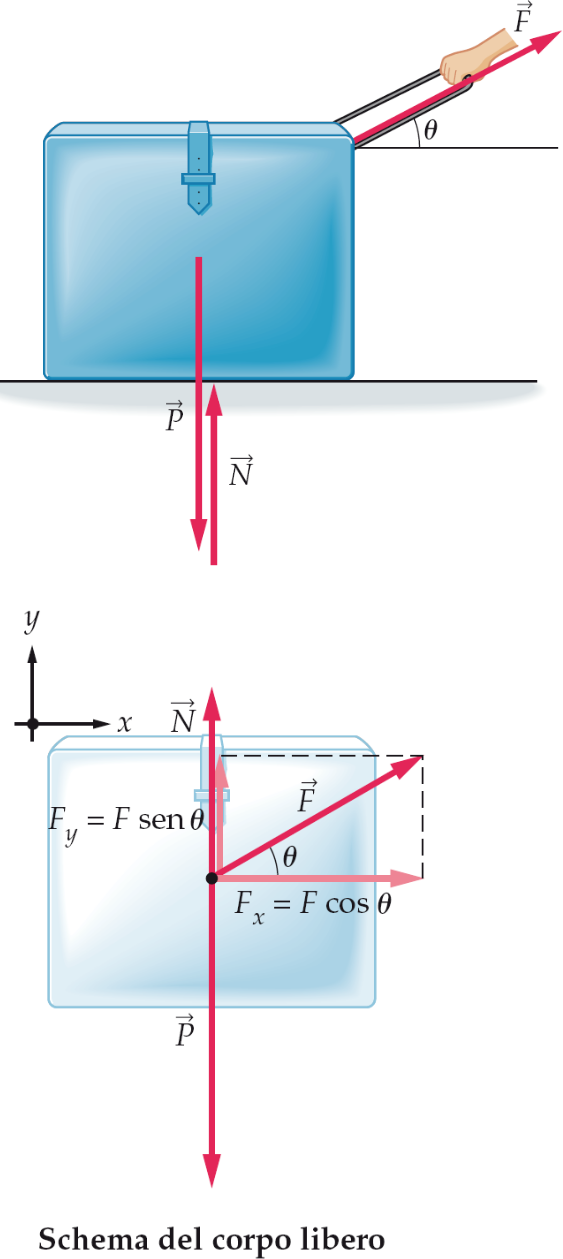
forze di attrito
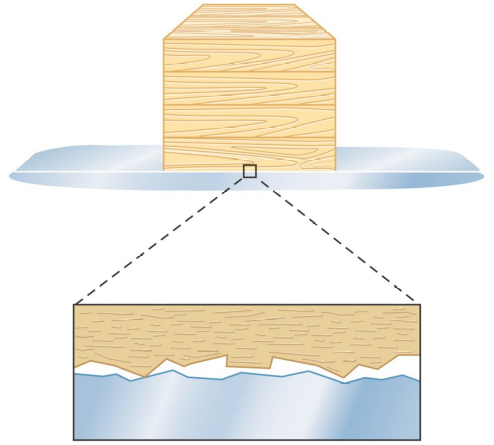
-
attrito statico: se proviamo a muovere un oggetto che è a contatto con una superficie, l’effetto della forza applicata non è immediato, perchè prima dobbiamo “smuoverlo”;
-
Attrito dinamico: quando l’oggetto si mette in moto, l’esperienza insegna che la forza da applicare per mantenere in moto l’oggetto è minore della forza necessaria per smuoverlo;
-
attrito e leggi di newton: se smettiamo di applicare la forza, l’oggetto si ferma. tali osservazioni sembrano contraddire il II principio della dinamica, ma non è così: questi effetti sono dovuti a forze, dette attriti, che si generano nel contatto tra l’oggetto e la superficie e si oppongono al moto.
attrito statico e dinamico:1
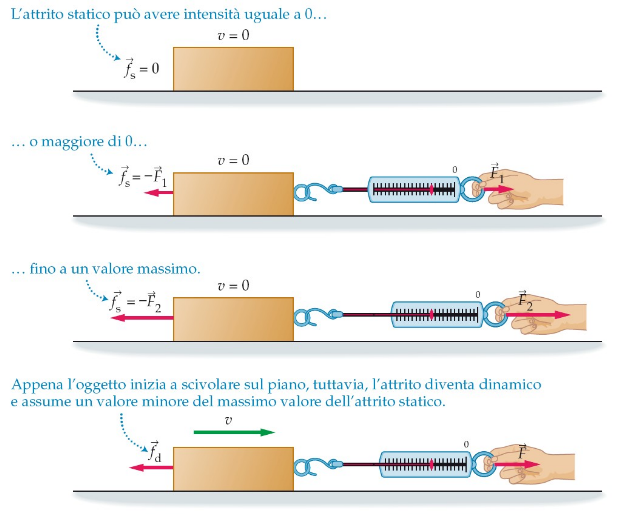
f_{s} \leq \mu_{s} \cdot N
attrito statico
f_{d} = \mu_{d} \cdot N
attrito dinamico
\mu_{s}, \, \mu_{d}
coefficienti di attrito
tensione in una fune
Tirando gli estremi di un pezzo di corda, la corda si tende; si dice che nella corda c’è una tensione.
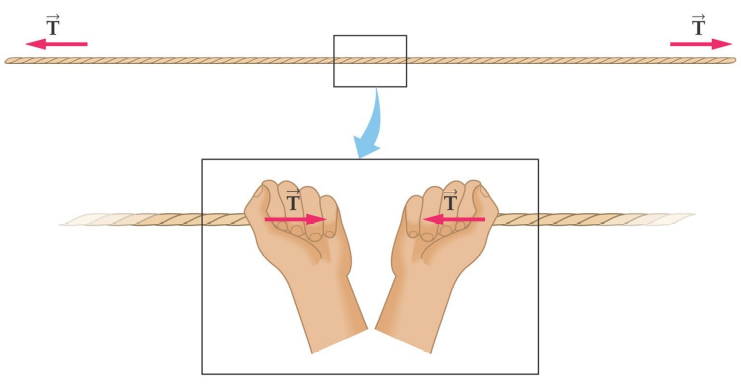
fune ideale
In una corda reale (dotata di massa), la tensione varia da un estremo all’altro a causa del peso della corda
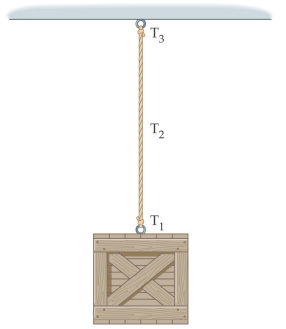
Nel seguito assumeremo che tutte le funi siano ideali, ossia prive di massa ed inestensibili
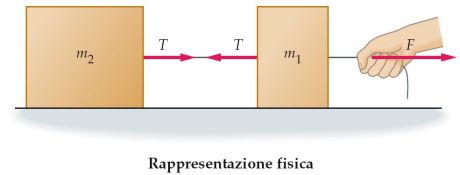
esercizio
carrucole
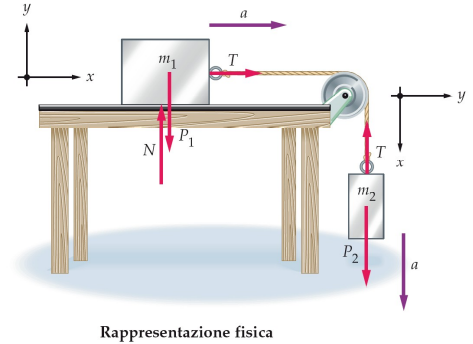
Una carrucola ideale cambia semplicemente la direzione della tensione, senza modificarne l’intensità.
forza elastica e moto armonico
\vec{F_{\mathrm{el}}}
x_{0}
\Delta x
k
m
Moto Circolare: 1
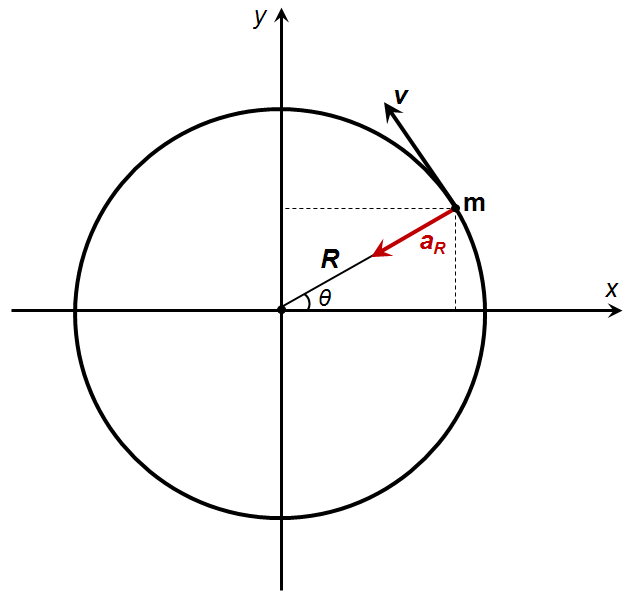
\bullet \; x(t) \, [m] \, \Rightarrow \, \theta(t) \, [rad] \;\;\;\;\;\;\;\;\;\; \\
\bullet \; v(t) \, [m/s] \, \Rightarrow \, \omega(t) \, [rad/s] \;\;\\
\bullet \; a(t) \, [m/s^{2}] \, \Rightarrow \, \alpha(t) \, [rad/s^{2}]
Moto Circolare: 1
\bullet \; x(t) \, [m] \, \Rightarrow \, \theta(t) \, [rad] \;\;\;\;\;\;\;\;\;\; \\
\bullet \; v(t) \, [m/s] \, \Rightarrow \, \omega(t) \, [rad/s] \;\;\\
\bullet \; a(t) \, [m/s^{2}] \, \Rightarrow \, \alpha(t) \, [rad/s^{2}]
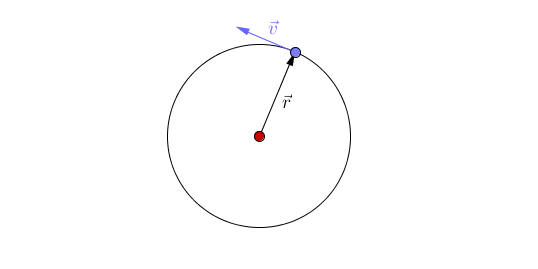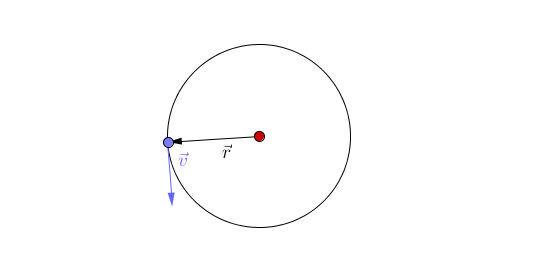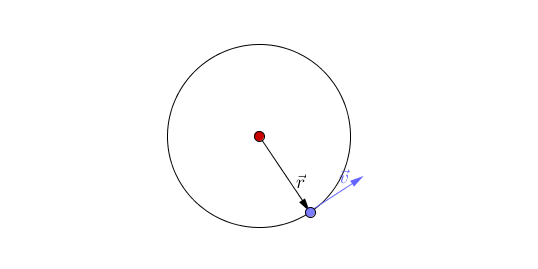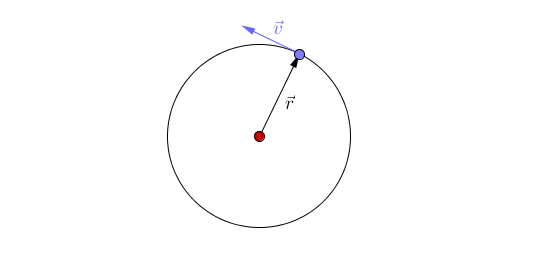
Moto Circolare: 2
derivazione dell'accelerazione centripeta
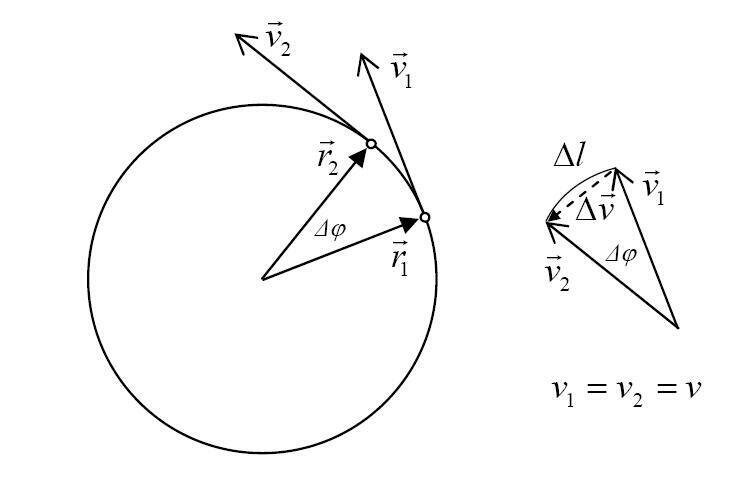
\frac{d \theta}{dt} = \omega = \frac{v}{r}
a_{c} = \omega^{2}r = \frac{v^{2}}{r}
forze e moto circolare
per il principio d'inerzia, un moto circolare non può avvenire in assenza di forze
\vec{v}
\vec{a_{\mathrm{N}}}
r
\vec{F}_{cp} = m \cdot \vec{a_{\mathrm{N}}}
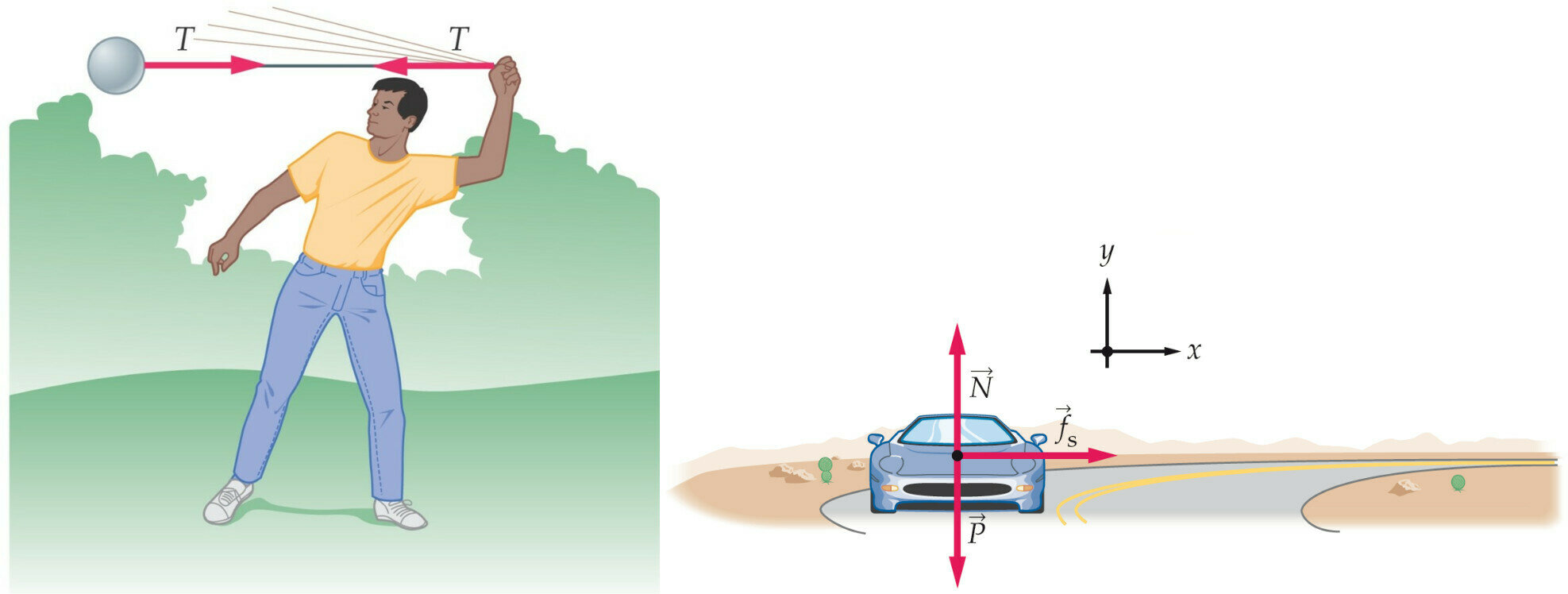
\vec{F}_{cp} = \vec{T}
\vec{F}_{cp} = \vec{f}_{s}
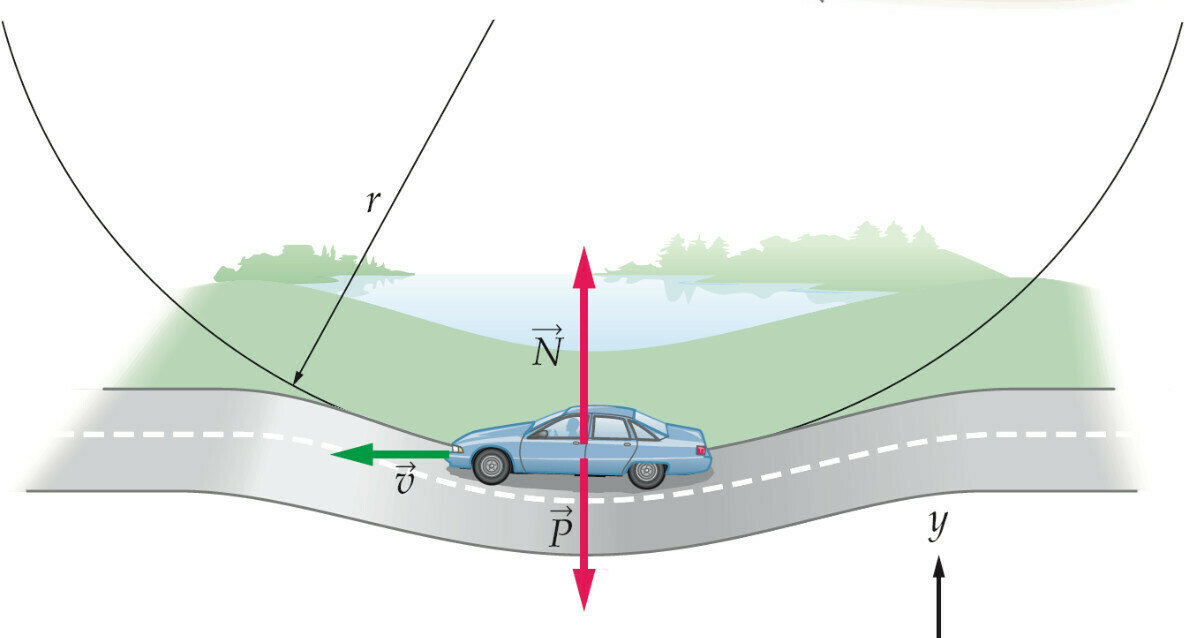
\vec{F}_{cp} = \vec{P}
forze e moto circolare
per il principio d'inerzia, un moto circolare non può avvenire in assenza di forze
\vec{F}_{cp} = m \cdot \vec{a_{\mathrm{N}}}
\vec{F}_{cp} = \vec{T}
\vec{F}_{cp} = \vec{f}_{s}
\vec{F}_{cp} = \vec{P}
forze e moto circolare
per il principio d'inerzia, un moto circolare non può avvenire in assenza di forze
\vec{F}_{cp} = m \cdot \vec{a_{\mathrm{N}}}
\vec{F}_{cp} = \vec{T}
\vec{F}_{cp} = \vec{f}_{s}
\vec{F}_{cp} = \vec{P}

moto circolare: 3
alcuni esempi
moto circolare: 4
moto circolare vs moto armonico
moto circolare: 5
moto circolare uniformemente accelerato
Musicologia: dinamica
By Giovanni Pellegrini
Musicologia: dinamica
- 61