BAND STRUCTURES
ELECTRONIC AND OPTICAL PROPERTIES
THE STARTING POINT: A 1D PERIODIC LATTICE OF ATOMS
a
-\frac{a}{2}
\frac{a}{2}
g = \frac{2 \pi}{a}
-\frac{g}{2}
\frac{g}{2}
x
k
Bravais Lattice: \(\{\vec{R}\}, \, \vec{R}=ma, \, m \in \mathbb{Z}\)
Reciprocal Lattice: \(\{\vec{G}\}, \, \vec{G}=lg, \, l \in \mathbb{Z}\)
Unit cell
Brillouin Zone
UNDERSTANDING THE BAND DIAGRAM
\begin{dcases}
\varphi_{nk}(x) = e^{ikx}\sum_{g_n}c_{k-g_n}e^{-g_n x} \\
f_{nk}(x) = \sum_{g_n}c_{k-g_n}e^{-g_n x}
\end{dcases}
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
AN EXAMPLE OF CENTRAL EQUATION
\bgroup
\def\arraystretch{2.0}
\left[
\begin{array}{ccccc}
\frac{\hbar^2}{2 m}(k-2 g)^2 & V_0 & 0 & 0 & 0 \\
V_0 & \frac{\hbar^2}{2 m}(k-g)^2 & V_0 & 0 & 0 \\
0 & V_0 & \frac{\hbar^2}{2 m} k^2 & V_0 & 0 \\
0 & 0 & V_0 & \frac{\hbar^2}{2 m}(k+g)^2 & V_0 \\
0 & 0 & 0 & V_0 & \frac{\hbar^2}{2 m}(k+2 g)^2
\end{array}\right]
\egroup
\left(\begin{array}{c}
c_{k-2 g} \\
c_{k-g} \\
c_k \\
c_{k+g} \\
c_{k+2 g}
\end{array}\right)=E_n\left(\begin{array}{c}
c_{k-2 g} \\
c_{k-g} \\
c_k \\
c_{k+g} \\
c_{k+2 g}
\end{array}\right)
ESTIMATING THE BAND GAP
V(x) = 2V_0 \cos(gx) = V_0e^{igx}+V_0e^{-igx}
\begin{gathered}
V_0 c_{k-g}+\left(\frac{\hbar^2}{2 m} k^2-E_n\right) c_k+V_0 c_{k+g}=0 \\
V_0 c_k+\left(\frac{\hbar^2}{2 m}(k+g)^2-E_n\right) c_{k+g}+V_0 c_{k+2 g}=0
\end{gathered}
\left(\begin{array}{cc}
\left(\frac{\hbar^2}{2 m} k^2-E_n\right) & V_0 \\
V_0 & \left(\frac{\hbar^2}{2 m}(k+g)^2-E_n\right)
\end{array}\right)\left(\begin{array}{c}
c_k \\
c_{k+g}
\end{array}\right)=\left(\begin{array}{l}
0 \\
0
\end{array}\right)
ESTIMATING THE BAND GAP
with \; k=-\frac{g}{2}
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
ESTIMATING THE BAND GAP
with \; k=-\frac{g}{2}
\left(\begin{array}{cc}
\left(\frac{\hbar^2}{2 m}\left(-\frac{g}{2}\right)^2-E_n\right) & V_0 \\
V_0 & \left(\frac{\hbar^2}{2 m}\left(\frac{g}{2}\right)^2-E_n\right)
\end{array}\right)\left(\begin{array}{l}
c_{-g / 2} \\
c_{g / 2}
\end{array}\right)=\left(\begin{array}{l}
0 \\
0
\end{array}\right)
An homogeneous system has a non-trivial solution only if the determinant of the coefficient matrix is zero
\left|\begin{array}{cc}
\frac{\hbar^2}{2 m}\left(\frac{g}{2}\right)^2-E_n & V_0 \\
V_0 & \frac{\hbar^2}{2 m}\left(-\frac{g}{2}\right)^2-E_n
\end{array}\right|=0
E_{\pm}=\frac{\hbar^2}{2 m}\left(\frac{g}{2}\right)^2 \pm V_0, \\[10pt]
E_{-}=E_{n}, \, E_{+}=E_{n+1}
E_g = E_{+}-E_{-} = 2V_0
FINDING THE EIGENFUNCTIONS
E_{+}=\frac{\hbar^2}{2 m}\left(\frac{g}{2}\right)^2 + V_0
\left(\begin{array}{cc}
-V_0 & V_0 \\
V_0 & -V_0
\end{array}\right)\left(\begin{array}{l}
c_{-g / 2} \\
c_{g / 2}
\end{array}\right)=\left(\begin{array}{l}
0 \\
0
\end{array}\right)
c_{-g / 2} = c_{g/2}
\varphi_{nk}(x) = e^{-i\frac{g}{2}x}(1+e^{igx})
\varphi_{nk}(x) \propto \cos \big(\frac{g}{2}x \big)
E_{-}=\frac{\hbar^2}{2 m}\left(\frac{g}{2}\right)^2 - V_0
\left(\begin{array}{cc}
V_0 & V_0 \\
V_0 & V_0
\end{array}\right)\left(\begin{array}{l}
c_{-g / 2} \\
c_{g / 2}
\end{array}\right)=\left(\begin{array}{l}
0 \\
0
\end{array}\right)
c_{-g / 2} = -c_{g/2}
\varphi_{nk}(x) = e^{-i\frac{g}{2}x}(1-e^{igx})
\varphi_{nk}(x) \propto \sin \big(\frac{g}{2}x \big)
Valence Band
Conduction Band
FINDING THE EIGENFUNCTIONS
\varphi_{nk}(x) \propto \cos \big(\frac{g}{2}x \big)
\varphi_{nk}(x) \propto \sin \big(\frac{g}{2}x \big)
Valence Band
Conduction Band
V(x) = 2V_0 \cos(gx) = V_0e^{igx}+V_0e^{-igx}
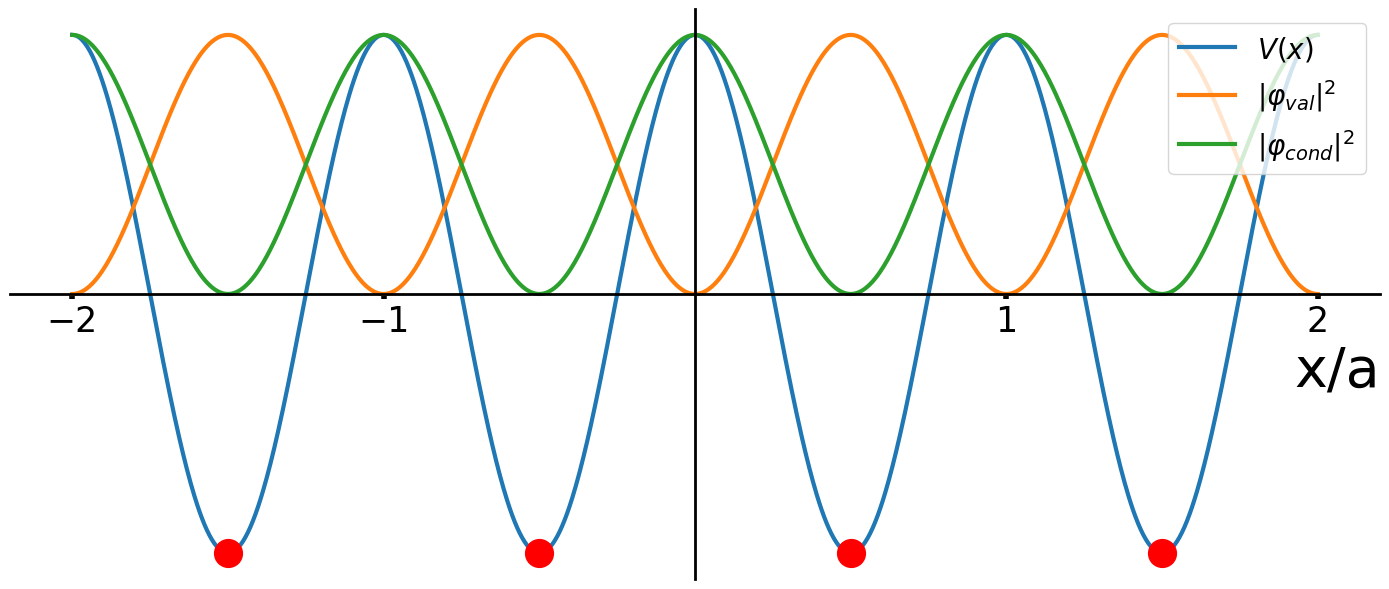
GENERAL SOLUTION
INTRODUCTION TO THE PARABOLIC APPROXIMATION
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
PARABOLIC APPROXIMATION: DIRECT BAND GAP
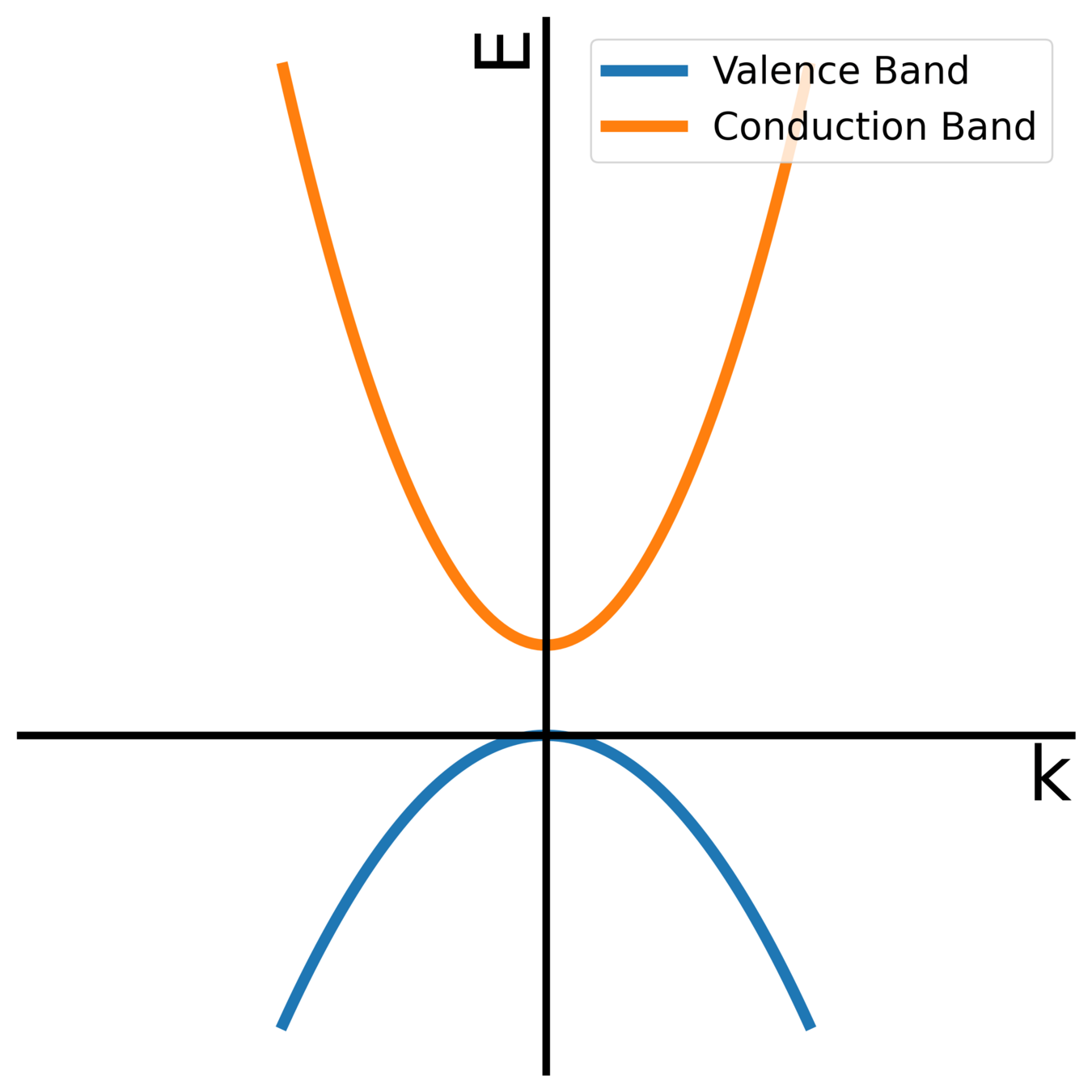

Electron in the valence band
Hole in the valence band
Electron in the conduction band
E_g
E_g
k = k - \frac{g}{2} \\
E = E - E_v
PARABOLIC APPROXIMATION: INDIRECT BAND GAP
Electron in the valence band
Hole in the valence band
Electron in the conduction band
E_g
E_g
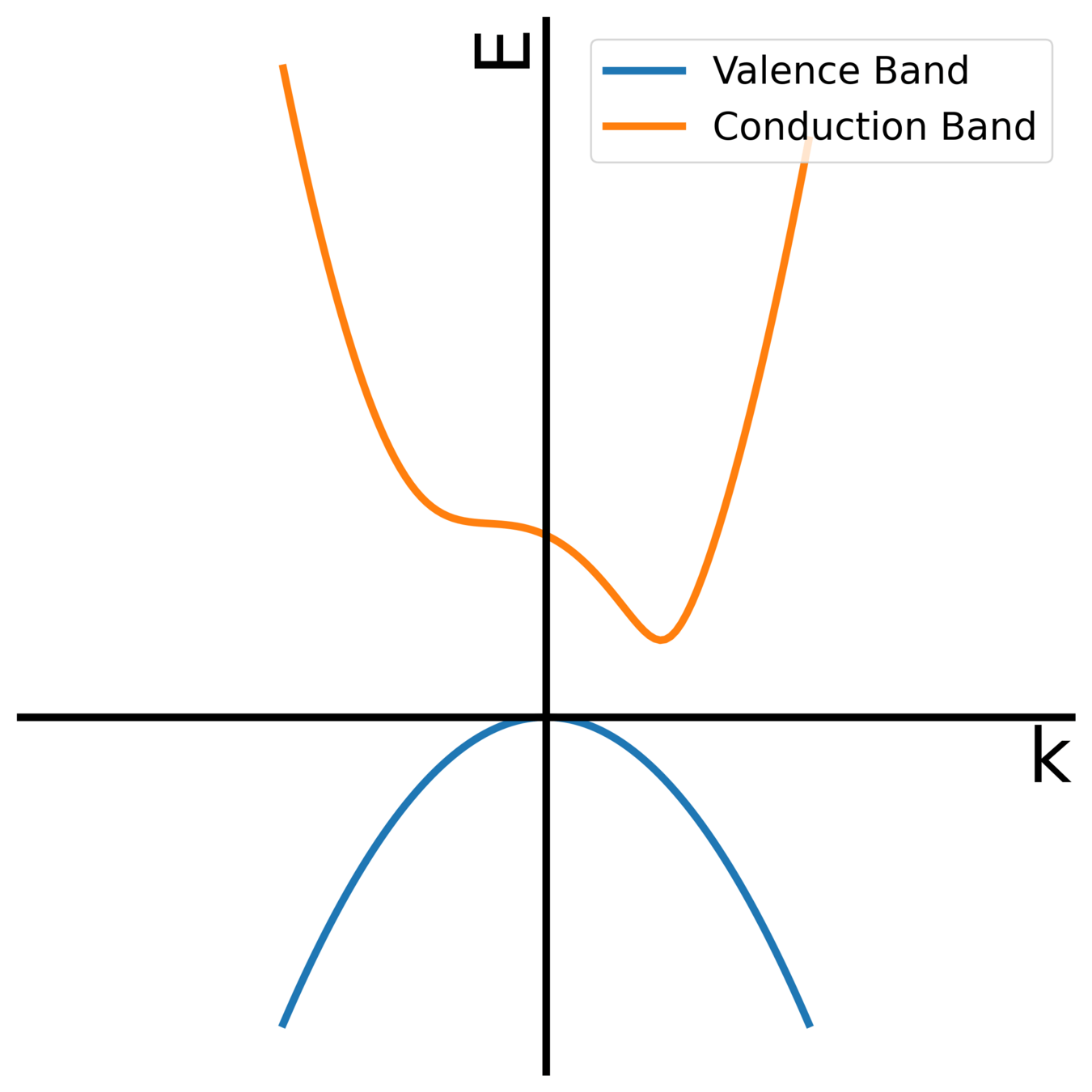

E_{vert}
k
PARABOLIC APPROXIMATION: INDIRECT BAND GAP
E_g

E_{vert}
k
Conservation of energy and momentum
\begin{dcases}
E = \hbar \Omega \\
p = \hbar k = \hbar \frac{\Omega}{v_{s}} \\
v_{s} = \frac{\Omega}{k} \\
\end{dcases}
Photon:
Lattice:
\begin{dcases}
E = \hbar \omega \\
p = \hbar k = \hbar \frac{\omega}{c} \\
c = \frac{\omega}{k} \\
\end{dcases}
BAND GAP IN MATERIALS
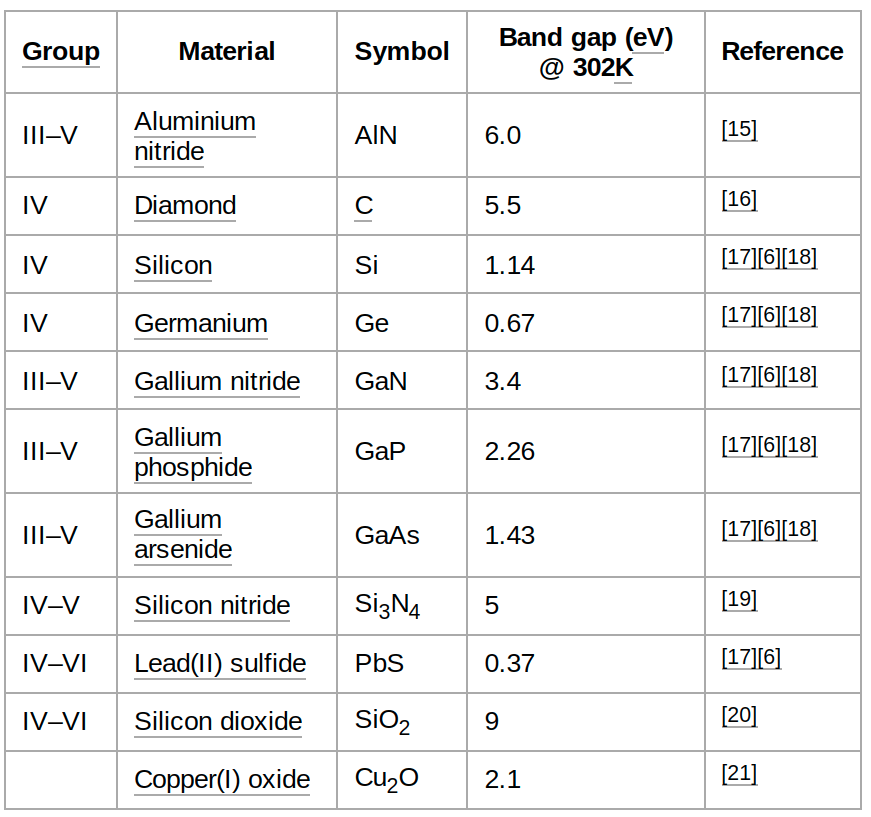
MOMENTUM OF THE ELECTRONS IN THE LATTICE
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
NON-DISPERSIVE WAVES PACKETS AND FOURIER TRANSFORMS
\hat{f}(k) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} f(x,0) e^{-ikx}
f(x,t) = \frac{1}{\sqrt{\pi}} \int^{-\infty}_{\infty} \hat{f}(k) e^{i(kx-\omega (k)t)}
v_g = \frac{d \omega (k)}{dk}
Group Velocity
NON-DISPERSIVE WAVES PACKETS AND FOURIER TRANSFORMS
v_{p} < v_{g}
v_{p} = v_{g}
v_{p} > v_{g}
MOMENTUM OF THE ELECTRONS IN THE LATTICE
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
\begin{cases}
v_g = \frac{d \omega (k)}{dk} \\
E = \hbar \omega
\end{cases}
\Rightarrow
v_g = \frac{1}{\hbar}\frac{d E (k)}{dk} \\
MOMENTUM EXPECTATION VALUE
\begin{dcases}
\varphi_{nk}(x) = e^{ikx}\sum_{g_n}c_{k-g_n}e^{-g_n x} \\
f_{nk}(x) = \sum_{g_n}c_{k-g_n}e^{-g_n x} \\
[\hat{p},\hat{H}] \neq 0
\end{dcases}
\Rightarrow
\begin{align*}
\left\langle p\right\rangle &= \left\langle \varphi_{nk}(x)|\hat{p}| \varphi_{nk}(x)\right\rangle \\[10pt]
& = \int_{-\infty}^{\infty} \varphi_{nk}^*(x)\left(-i \hbar \frac{\partial}{\partial x} \varphi_{nk}(x)\right) d x \\[10pt]
& = \sum_{g_{n}}\left|c_{k-g_{n}}\right|^2 \hbar(k-g_{n})
\end{align*}
\left\langle p\right\rangle = \left\langle \sin \big(\frac{g}{2}x\big)|\hat{p}| \sin\big(\frac{g}{2}x\big)\right\rangle
\left\langle p\right\rangle = \left\langle \cos \big(\frac{g}{2}x\big)|\hat{p}| \cos\big(\frac{g}{2}x\big)\right\rangle
Valence Band
Conduction Band
PARABOLIC BANDS: EFFECTIVE MASSES

\begin{dcases}
E_{v, c}(k) \approx E_{v, c}(0)+\frac{1}{1!} \frac{\partial E_{v, c}(0)}{\partial k} k+\frac{1}{2!} \frac{\partial^2 E_{v, c}(0)}{\partial k^2} k^2+\ldots \\
\frac{\partial E_{v, c}}{\partial k}(0)=0
\end{dcases}
\begin{dcases}
E_v(k)=\frac{1}{2} \frac{\partial^2 E_v}{\partial k^2}(0) k^2 \\
E_c(k)=E_g+\frac{1}{2} \frac{\partial^2 E_c}{\partial k^2}(0) k^2
\end{dcases}
\begin{dcases}
\frac{1}{m_{v}^*}=-\frac{1}{\hbar^2} \frac{\partial^2 E_{v}}{\partial k^2} \\
\frac{1}{m_{c}^*}=\frac{1}{\hbar^2} \frac{\partial^2 E_{c}}{\partial k^2}
\end{dcases}
EFFECTIVE MASS AND ELECTRONICS

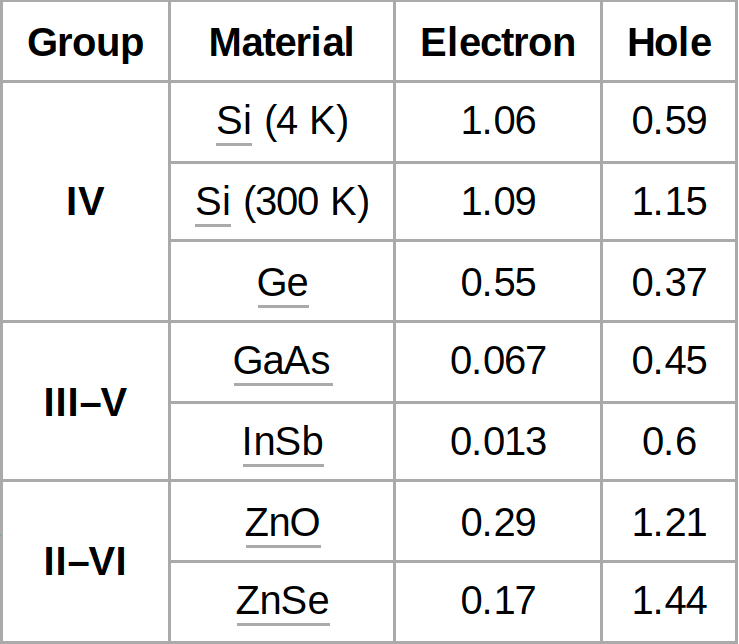
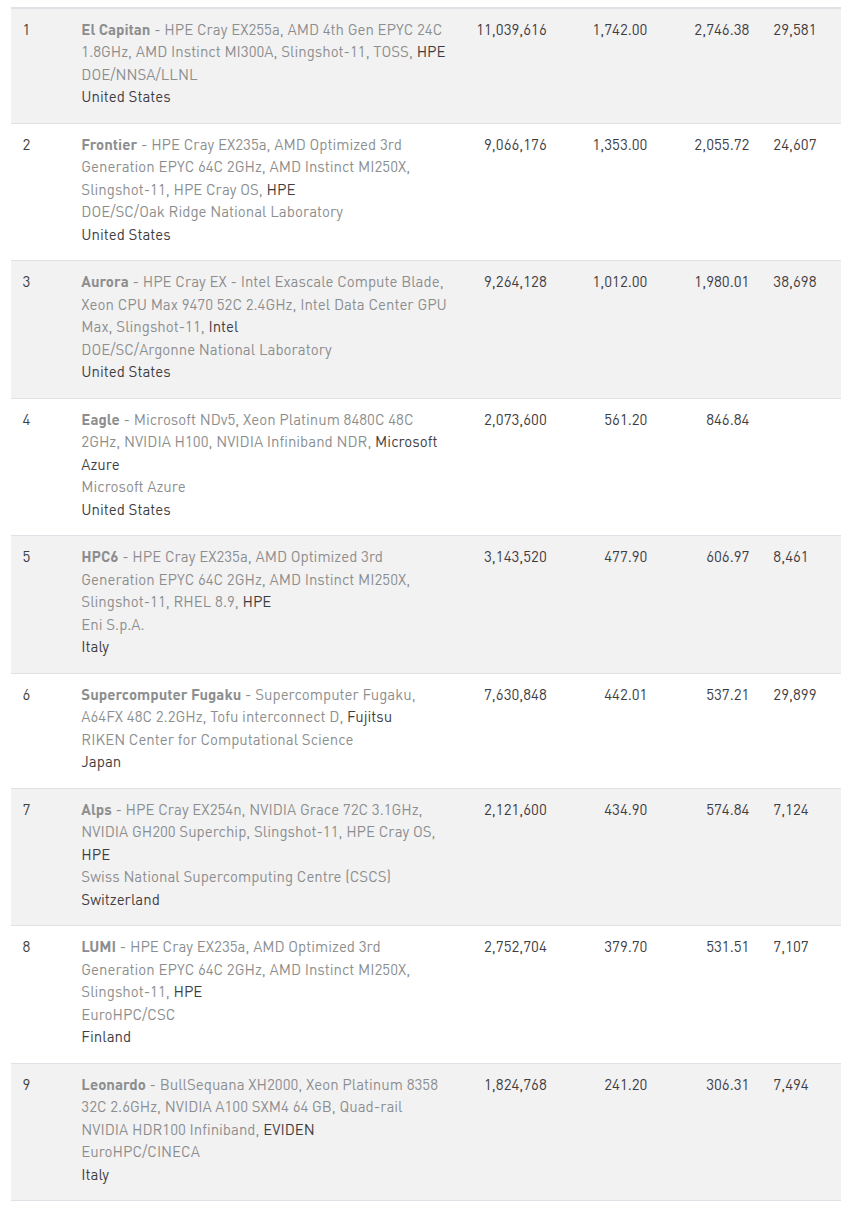
EFFECTIVE MASS: TOP500 AND CRAY

SEIMOUR CRAY AND THE CRAY-2


THE CRAY-3 RUNNING ON GaAs


Materials and Platforms for AI - Band Structure: Electronic and Optical Properties
By Giovanni Pellegrini
Materials and Platforms for AI - Band Structure: Electronic and Optical Properties
- 139



