QUANTUM MECHANICS
MEASUREMENTS AND SYMMETRIES
OBSERVABLES AND OPERATORS
All observables are associated to an Hermitian operator
a \rightarrow \hat{A}
A set of eigenvalues and eigenfunctions are associated to the operator
\hat{A} \phi_n = a_n \phi_n
The eigenfunctions for a complete orthonormal basis
\braket{\phi_m | \phi_n} = \delta_{mn}
OUTCOME OF A MEASUREMENT
3d Postulate of Q.M.
In any measurement of the observable associated with operator \(\hat{A}\) the only values that will ever be observed
are the eigenvalues \(a_n\) that satisfy the eigenvalue equation \(\hat{A} \phi_{n} = a_{n} \phi_{n}\), indepentently of the initial state of the system \(\psi(x,t)\)
A measurement of a quantum mechanical system perturbs it and leads to the so called "collapse of the wavefunction"
PROBABILISTIC NATURE OF A QUANTUM MEASUREMENT
When performing a measurement of the observable associated with operator \(\hat{A}\), given an initial quantum state:
\[\psi(x) = \sum_{n}c_n\phi_n\]
what is the probability of observing the eigenvalue \(a_n\) associated to the eigenfunction \(\phi_n\) as an outcome of the measurement?
MEASUREMENT EXAMPLES
Free Particle
Particle in a Box
\begin{dcases}
\phi_k(x) = e^{ikx} \\[10pt]
\hat{p} = -i \hbar \frac{d}{dx} \\[10pt]
p = \hbar k
\end{dcases}
\begin{dcases}
\phi_n(x) =
\begin{dcases}
\sqrt{\frac{2}{d}}cos(k_n x), \, n \, odd \\[10pt]
\sqrt{\frac{2}{d}}sin(k_n x), \, n \, even \\[10pt]
\end{dcases} \\[10pt]
\hat{H} = - \frac{\hbar^2}{2m} \frac{d^2}{dx^2} \\[10pt]
E = \frac{\hbar^2 k_n^2}{2m}, \, k_n = \frac{n \pi}{d}
\end{dcases}
\psi(x) = \frac{1}{2}e^{i k_0 x} + \frac{1}{2}e^{i 2 k_0 x} + \frac{\sqrt{2}}{2}e^{-i k_0 x}
\psi(x) = \frac{1}{3} \sqrt{\frac{2}{d}}cos \bigg(\frac{\pi x}{d}\bigg) +
\frac{2}{3} \sqrt{\frac{2}{d}}sin \bigg(\frac{2 \pi x}{d}\bigg) +
\frac{2}{3} \sqrt{\frac{2}{d}}sin \bigg(\frac{4 \pi x}{d}\bigg)
EXPECTATION VALUE OF A MEASUREMENT
\begin{dcases}
\psi(x) = \sum_n c_n \phi_n \\[10pt]
\hat{A}\phi_n = a_n \phi_n \\[10pt]
\langle A \rangle = \braket{\psi|\hat{A}|\psi} = \int \psi^*(x) \hat{A} \psi(x) dx = \sum_n a_n |c_n|^2
\end{dcases}
PRECISION OF A QUANTUM MEASUREMENT
[\hat{A},\hat{B}] = \hat{A}\hat{B}-\hat{B}\hat{A}
Fundamental Theorem of Algebra
If two operators \(\hat{A}\) and \(\hat{B}\) commute one can construct a basis of the state space with eigenfunctions common to \(\hat{A}\) and \(\hat{B}\), conversely if a basis set is found of eigenfunctions common to both \(\hat{A}\) and \(\hat{B}\) then \(\hat{A}\) and \(\hat{B}\) commute.
[\hat{H},\hat{p}] = 0
[\hat{x},\hat{p}] = i \hbar
HEISEMBERG'S UNCERTAINTY PRINCIPLE
\Delta A \cdot \Delta B \geq \frac{|[\hat{A},\hat{B}]|}{2}
\begin{dcases}
\Delta x \cdot \Delta p \geq \frac{|[\hat{x},\hat{p}]|}{2} = \frac{\hbar}{2} \\[10pt]
\Delta E \cdot \Delta t \geq \frac{|[\hat{E},\hat{t}]|}{2} = \frac{\hbar}{2}
\end{dcases}
\frac{d\langle \hat{A} \rangle}{dt} = \frac{1}{i \hbar} \langle [\hat{A},\hat{H}] \rangle + \bigg\langle \frac{\partial \hat{A} }{\partial t} \bigg \rangle
\frac{d\langle \hat{A} \rangle}{dt} = 0 \iff
\begin{dcases}
\frac{1}{i \hbar} \langle [\hat{A},\hat{H}] \rangle = 0 \\[10pt]
\bigg\langle \frac{\partial \hat{A} }{\partial t} \bigg \rangle = 0
\end{dcases}
CONSERVED QUANTITIES: EHRENFEST THEOREM
\frac{d\langle \hat{A} \rangle}{dt} = \frac{1}{i \hbar} \langle [\hat{A},\hat{H}] \rangle + \bigg\langle \frac{\partial \hat{A} }{\partial t} \bigg \rangle
\begin{dcases}
\hat{A} = \hat{H} \\[10pt]
\hat{A} = \hat{p}
\end{dcases}
Time independent Hamiltonian
Momentum for free particle
EXAMPLE OF CONSERVED QUANTITIES
Classical
Quantum
\vec{L}= \vec{r} \times \vec{p}=
\begin{vmatrix}
\vec{u}_x & \vec{u}_y & \vec{u}_z \\
x & y & z \\
p_x & p_y & p_z
\end{vmatrix}
\begin{dcases}
L_x = y p_z - z p_y \\[10pt]
L_y = z p_x - x p_z \\[10pt]
L_z = x p_y - y p_x \\[10pt]
\end{dcases}
\hat{L}= \vec{r} \times \hat{p}=
\begin{vmatrix}
\vec{u}_x & \vec{u}_y & \vec{u}_z \\
x & y & z \\
-i \hbar \frac{\partial}{\partial x} & -i \hbar \frac{\partial}{\partial y} & -i \hbar \frac{\partial}{\partial z}
\end{vmatrix}
\begin{dcases}
L_x = i \hbar (z \frac{\partial}{\partial y} - y \frac{\partial}{\partial z}) \\[10pt]
L_y = i \hbar (x \frac{\partial}{\partial z} - z \frac{\partial}{\partial x}) \\[10pt]
L_z = i \hbar (y \frac{\partial}{\partial x} - x \frac{\partial}{\partial y}) \\[10pt]
\end{dcases}
HYDROGEN ATOM: ANGULAR MOMENTUM
HYDROGEN ATOM: ANGULAR MOMENTUM
Cartesian
Spherical
\begin{dcases}
\hat{L}_x = i \hbar \left( \sin\phi \frac{\partial}{\partial \theta} + \frac{\cos\phi}{\tan\theta} \frac{\partial}{\partial \phi} \right) \\[10pt]
\hat{L}_y = i \hbar \left( -\cos\phi \frac{\partial}{\partial \theta} + \frac{\sin\phi}{\tan\theta} \frac{\partial}{\partial \phi} \right) \\[10pt]
\hat{L}_z = -i \hbar \frac{\partial}{\partial \phi}
\end{dcases}
\begin{dcases}
\hat{L}_x = i \hbar (z \frac{\partial}{\partial y} - y \frac{\partial}{\partial z}) \\[10pt]
\hat{L}_y = i \hbar (x \frac{\partial}{\partial z} - z \frac{\partial}{\partial x}) \\[10pt]
\hat{L}_z = i \hbar (y \frac{\partial}{\partial x} - x \frac{\partial}{\partial y}) \\[10pt]
\end{dcases}
\hat{L}^2 = \hat{L}_x^2 + \hat{L}_y^2 + \hat{L}_z^2
\hat{L}^2 = -\hbar^2 \bigg( \frac{\partial^2}{\partial \theta^2} + \frac{1}{\tan\theta}\frac{\partial}{\partial\theta} +
\frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\bigg)
HYDROGEN ATOM: MOMENTUM COMMUTATORS
[\hat{L}_x,\hat{L}_y]=i \hbar \hat{L}_{z} \\
[\hat{L}_y,\hat{L}_z]=i \hbar \hat{L}_{x} \\
[\hat{L}_z,\hat{L}_x]=i \hbar \hat{L}_{y} \\
[\hat{L}^2,\hat{L}_{x,y,z}]=0
HYDROGEN ATOM: SPHERICAL HARMONICS
EIGENFUNCTIONS OF THE MOMENTUM OPERATORS
\begin{dcases}
\hat{L}_z Y_l^m(\theta,\phi) = m \hbar Y_l^m(\theta,\phi) \\[10pt]
\hat{L}^2 Y_l^m(\theta,\phi) = \hbar^2 l (l+1) Y_l^m(\theta,\phi)
\end{dcases}
with \(l=0,1,2,3,...\)
and \( -l \le m \le l\)
Y_l^m(\theta,\phi) =
\begin{dcases}
(-1)^m \sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}P_l^m(\cos\theta)e^{im\phi}, \, m \geq 0 \\[20pt]
\sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}P_l^{-m}(\cos\theta)e^{im\phi}, \, m < 0
\end{dcases}
SPHERICAL HARMONICS PLOTS
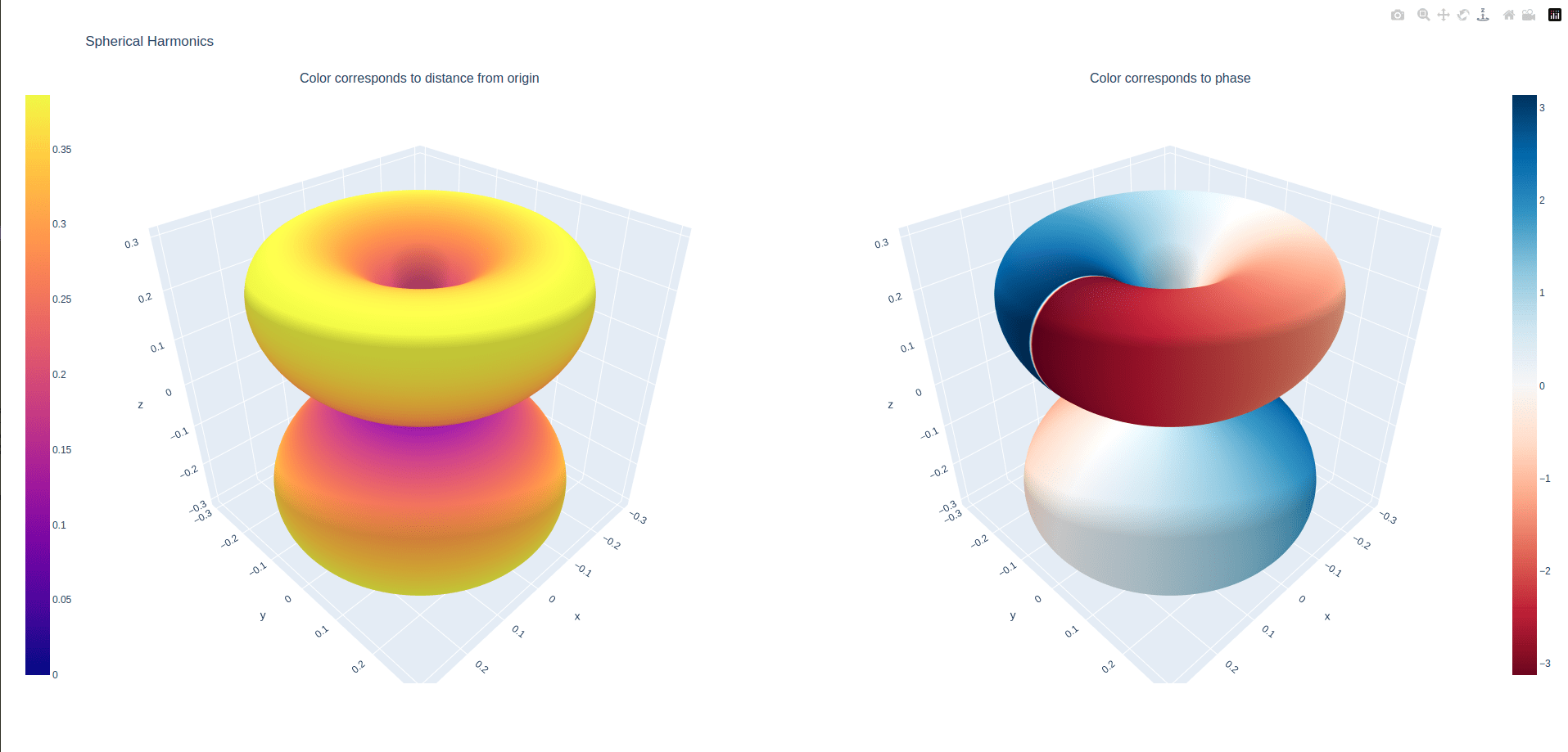
HYDROGEN ATOM: HAMILTONIANS
H(\vec{r}_e,\vec{r}_p,\vec{p}_e,\vec{p}_p) = \frac{p_p^2}{2m_p} + \frac{p_e^2}{2m_e} - \frac{1}{4 \pi \varepsilon_0} \frac{e^2}{|\vec{r}_e-\vec{r}_p|}
CM:
\begin{dcases}
M = m_p + m_e \\[10pt]
\vec{P}_{CM} = \vec{p}_p + \vec{p}_e \\[10pt]
\vec{R}_{CM} = \frac{m_p \vec{r}_p + m_e \vec{r}_e}{m_p+m_e}
\end{dcases}
Rel:
\begin{dcases}
\mu = \frac{m_p m_e}{m_p + m_e} \\[10pt]
\vec{p} = \frac{m_e \vec{p}_p - m_p \vec{p}_e}{m_e+m_p} \\[10pt]
\vec{r} = \vec{r}_e - \vec{r}_{p}
\end{dcases}
H(\vec{R}_{CM},\vec{r},\vec{P}_{CM},\vec{p}) = \frac{p_{CM}^2}{2M} + \frac{p^2}{2\mu} - \frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r}
\vec{r}_p
\vec{r}_e
\vec{r}_e-\vec{r}_p
+e
-e
HYDROGEN ATOM: BOHR'S MODEL
\begin{dcases}
H(\vec{r},\vec{p}) = \frac{p^2}{2\mu} - \frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r} \\[10pt]
|\vec{r} \times \vec{p}| = m r v_t \\[10pt]
\mu \frac{v_t^2}{r} = \frac{1}{4 \pi \varepsilon_0}\frac{e^2}{r^2} \\[10pt]
L = n \hbar \\[10pt]
\end{dcases}
\vec{v}_t
\vec{r}
+e
-e
\vec{F}_c
\vec{F}_{el}
r_n = n^2 a_0
E_n = -\frac{1}{n^2}\frac{1}{(4 \pi \varepsilon_0)^2}\frac{\mu e^4}{2 \hbar^2}
a_0 = \frac{4 \pi \varepsilon_0 \hbar^2}{\mu e^2}
Bohr's Radius
QUANTUM MECHANICAL HYDROGEN ATOM
\hat{H}(\hat{\vec{r}},\hat{\vec{P}}_{CM},\hat{\vec{p}}) = \frac{\hat{P}_{CM}^2}{2M} + \frac{\hat{p}^2}{2\mu} - \frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r} = \hat{H}_{CM} + \hat{H}_r
[\hat{H}_{CM},\hat{H}_r]=0 \Rightarrow \hat{H}_r = \frac{\hat{p}^2}{2\mu} - \frac{1}{4 \pi \varepsilon_0}
\hat{H}_r(\hat{\vec{r}},\hat{\vec{p}}) = -\frac{\hbar^2}{2 \mu}\bigg( \frac{1}{r}\frac{\partial^2}{\partial r^2}r +
\frac{1}{r^2} \bigg(\frac{\partial^2}{\partial\theta^2} + \frac{1}{\tan\theta}\frac{\partial}{\partial\theta}+
\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial\phi^2} \bigg) \bigg) - \frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r}
\hat{H}_r(\hat{\vec{r}},\hat{\vec{p}}) = -\frac{\hbar^2}{2 \mu} \frac{1}{r}\frac{\partial^2}{\partial r^2}r +
\frac{\hat{L}^2}{2 \mu r^2} - \frac{1}{4 \pi \varepsilon_0}\frac{e^2}{r}
QUANTUM MECHANICAL HYDROGEN ATOM
\begin{dcases}
[\hat{H}_r,\hat{L}^2]=0 \\[10pt]
[\hat{H}_r,\hat{L}_z]=0
\end{dcases}
\Rightarrow
\begin{dcases}
\hat{L}_z \psi(r,\theta,\phi) = m\hbar \psi(r,\theta,\phi) \\[10pt]
\hat{L}^2 \psi(r,\theta,\phi) = \hbar^2 l(l+1)\psi(r,\theta,\phi) \\[10pt]
\hat{H}_r \psi(r,\theta,\phi) = E\psi(r,\theta,\phi)
\end{dcases}
\psi_{nlm}(r,\theta,\phi) = R_{nl}(r)Y_l^m(\theta,\phi)
\bigg[ -\frac{\hbar^2}{2 \mu} \frac{1}{r}\frac{\partial^2}{\partial r^2}r +
\frac{\hbar^2 l(l+1)}{2 \mu r^2} - \frac{1}{4 \pi \varepsilon_0}\frac{e^2}{r} \bigg]R_{nl}(r) = E_{nl} R_{nl}(r)
RADIAL WAVEFUNCTIONS
\bigg[ -\frac{\hbar^2}{2 \mu} \frac{1}{r}\frac{\partial^2}{\partial r^2}r +
\frac{\hbar^2 l(l+1)}{2 \mu r^2} - \frac{1}{4 \pi \varepsilon_0}\frac{e^2}{r} \bigg]R_{nl}(r) = E_{n} R_{nl}(r)
R_{nl}(r) = \sqrt{\bigg(\frac{2}{n}\bigg)^3 \frac{(n-l-1)!}{2n(n+l)!}} \bigg(\frac{r}{n a_0}\bigg)^l e^{-\frac{r}{n a_0}} L_{n-l-1}^{2l+1}\bigg(\frac{2r}{n a_0}\bigg),
\, n>l, \, l \geq 0
\braket{nl|n'l} = \int_0^\infty R^*_{nl}(r)R_{n'l}(r)r^2dr = \delta_{nn'}
PLOT OF RADIAL WAVEFUNCTIONS
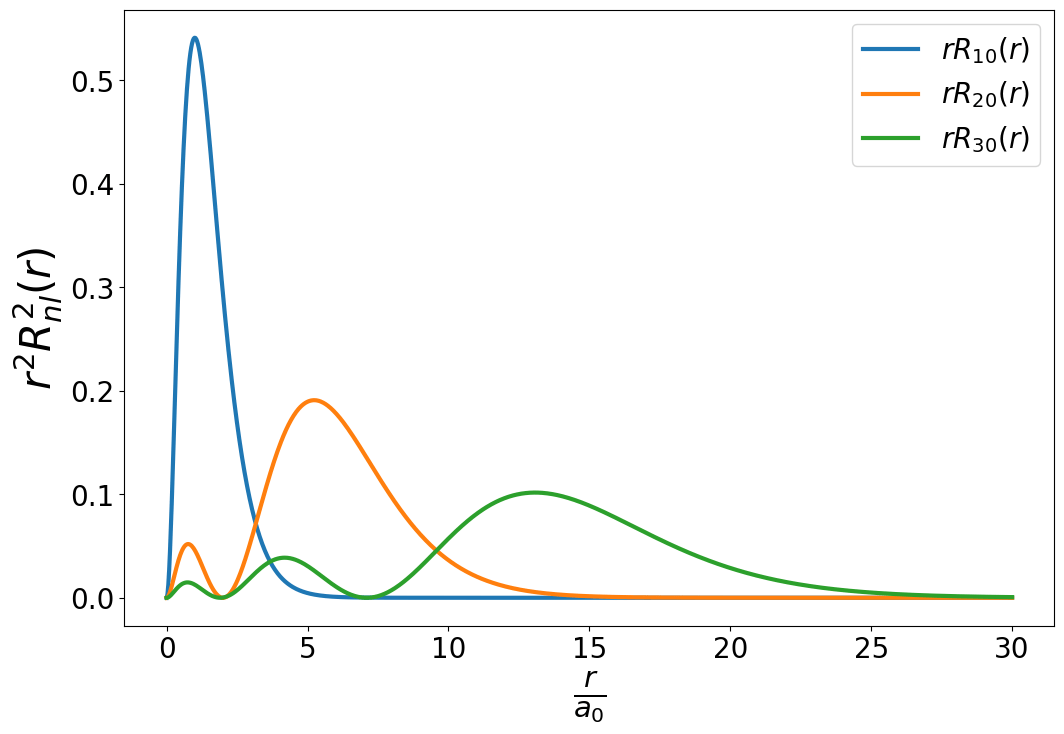
ATOMIC ORBITALS
Materials and Platforms for AI - Measurements and Symmetries
By Giovanni Pellegrini
Materials and Platforms for AI - Measurements and Symmetries
- 146



