NEWTONIAN AND HAMILTONIAN MECHANICS
MECHANICS
Study of the motion of a body and its causes
- Quantitative laws
- Dynamics of an ideal point
KINEMATICS
We just study the motion of a body, not its causes
Fundamental quantities: space - time - velocity - acceleration
Space ⮕ Velocity ⮕ Acceleration
v_{m} = \frac{\Delta S}{\Delta t};
v(t) = \lim\limits_{\Delta t\to 0} \frac{\Delta S}{\Delta t} = \frac{dS}{dt}
a(t) = \lim\limits_{\Delta t\to 0} \frac{\Delta v}{\Delta t} = \frac{dv}{dt}
a_{m} = \frac{\Delta v}{\Delta t};
\Delta S
S(t)
\frac{d}{dt}
\frac{d}{dt}
Average
Istantaneous
Acceleration ⮕ Velocity ⮕ Space
\Delta v = a_{m} \Delta t
v(t) = v_{0} + \int_{0}^{t} a(t') \,dt'
\Delta S = v_{m}{\Delta t}
a_{m}
a(t)
\int_{0}^{t} dt'
Average
Istanteneous
\int_{0}^{t} dt'
s(t) = s_{0} + \int_{0}^{t} v(t') \,dt'
Uniformly accelerated motion
a(t) = a_{0}
NEWTON'S LAWS
FIRST NEWTON'S LAW
The Principle of Inertia
Every object perseveres in its state of rest, or of uniform motion in a right line, except insofar as it is compelled to change that state by forces impressed thereon.
An inertial frame of reference is one in which the motion of a particle not subject to forces is in a straight line at constant speed.
NEWTON'S SECOND LAW
The change of motion of an object is proportional to the force impressed; and is made in the direction of the straight line in which the force is impressed.
\, \vec{F}=m\vec{a} = \frac{d\vec{p}}{dt} \,
Law of motion
[\mathrm{Kg \cdot m \cdot s^{-2}}]
[N]
NEWTON'S THIRD LAW
To every action, there is always opposed an equal reaction; or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts
\, \vec{F_{12}}=-\vec{F_{21}} \,
Law of action and reaction
WORK OF A CONSTANT FORCE
Along a straight line
\bullet \; L=\vec{F} \cdot \vec{s} = F \cdot x \cdot cos(\theta)
\bullet \; Joule \Rightarrow [Kg \cdot m^{2} \cdot s^{-2}]
WORK: GENERAL CASE
\bullet \; \Delta L_{1} = \vec{F}_{1} \cdot \Delta \vec{s}_{1}
\bullet \; \Delta L_{2} = \vec{F}_{2} \cdot \Delta \vec{s}_{2}
\bullet \; \ldots
\bullet \; \ldots
\bullet \; \Delta L_{n} = \vec{F}_{n} \cdot \Delta \vec{s}_{n}
L=\lim _{\Delta s \rightarrow 0} \sum_i \vec{F}_i \cdot \Delta \vec{s}_1=\int_1^2 \vec{F} \cdot d \vec{s}
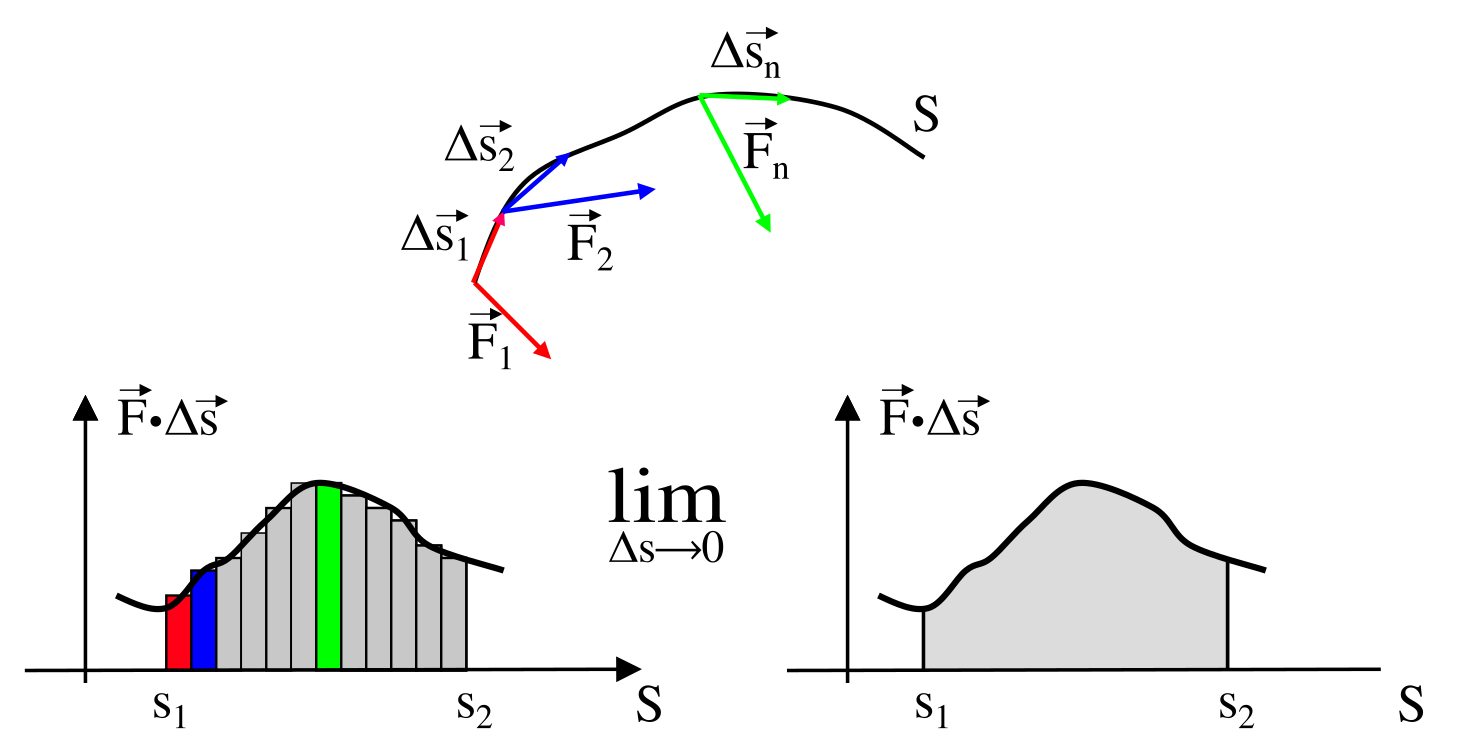
WORK: CONSERVATIVE FORCES
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(3)}
L_{A \rightarrow B}^{(2)}
=
=
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(n)} + L_{B \rightarrow A}^{(m)} = 0
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(3)}
L_{A \rightarrow B}^{(2)}
\neq
\neq
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(n)} + L_{B \rightarrow A}^{(m)} \neq 0
Conservative Forces
Non-Conservative Forces
A Conservative Force: the elestic Force
L_{A \rightarrow B}^{(n)} = L_{A \rightarrow B}^{(m)} = L_{A \rightarrow B}^{(l)}
L_{A \rightarrow B}^{(n)} = -\frac{1}{2}k(x^{2}_{B}-x^{2}_{A})
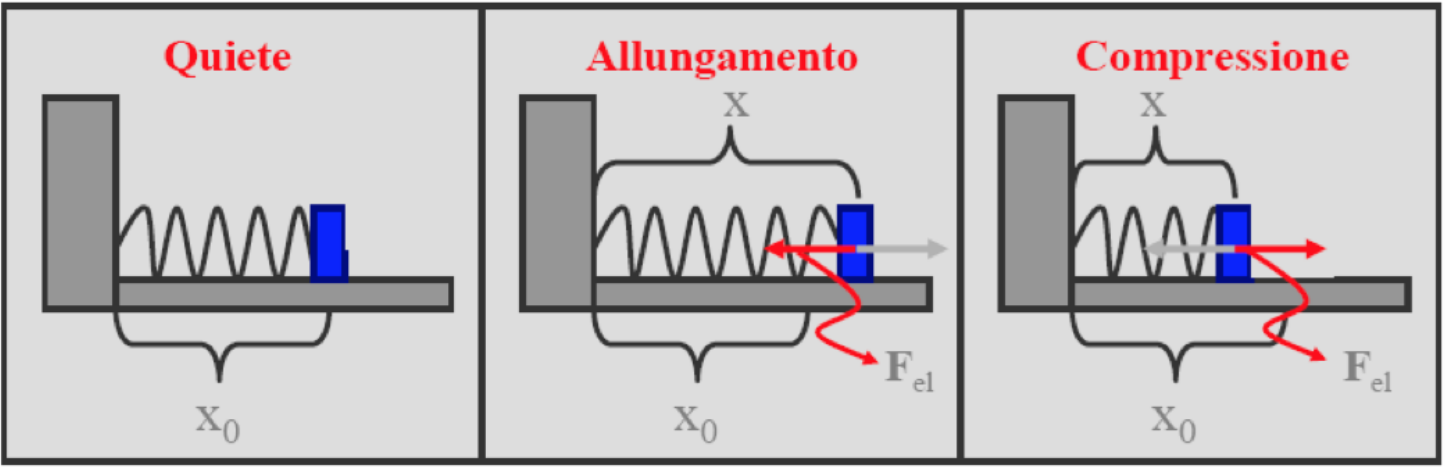
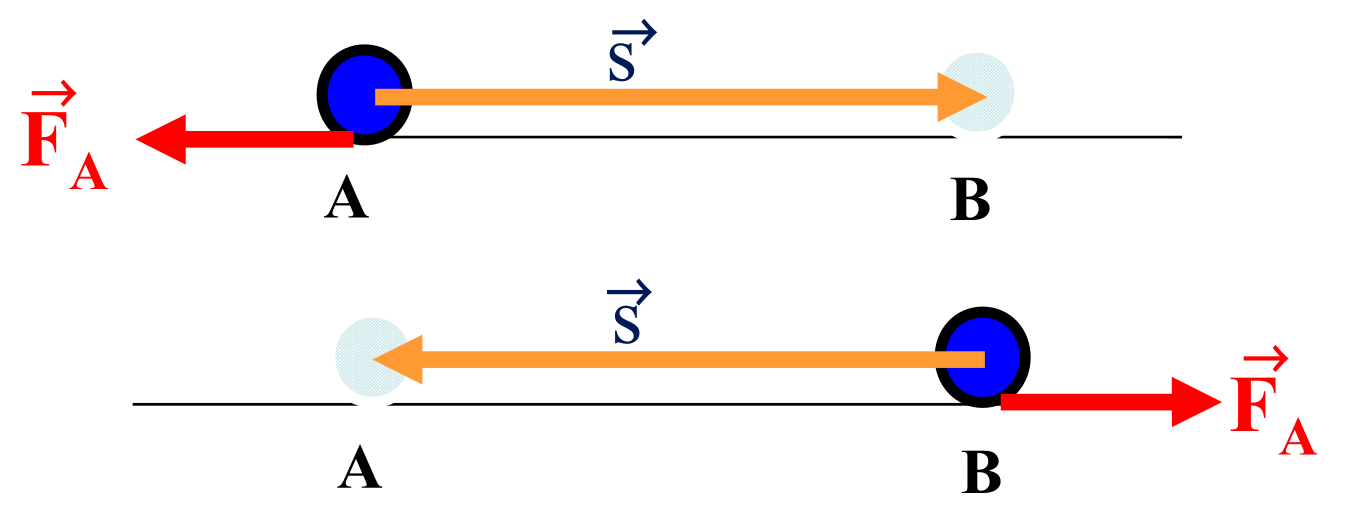
A non-conservative force: friction
L_{A \rightarrow B}^{(n)} + L_{B \rightarrow A}^{(m)} \neq 0
L_{A \rightarrow B} + L_{B \rightarrow A} = -2 \cdot F_{\mu_{d}} \cdot s
THE IDEA OF ENERGY
Energy, in physics, the capacity for doing work.
Forms of Energy
- Kinetic
- Gravitational
- Elastic
- Thermal
- Chemical
- Nuclear
THE PRINCIPLE OF CONSERVATION OF ENERGY
The total energy of an isolated system remains constant
If energy appears not to be conserved, the explanations lies in a source of dissipation that has not been accounted for
\Delta E_{tot}=0
E_{tot}=cost
KINETIC ENERGY
The kinetic energy of an object is the form of energy that it possesses due to its motion.
T = \frac{1}{2}mv^{2} = \frac{p^2}{2 m}
Work energy theorem
L = \Delta T = \frac{1}{2}m(v^{2}_{f}-v^{2}_{i})
CONSERVATIVE FORCES AND POTENTIAL ENERGY
Potential energy (U) is associated with forces that act on a body in a way that the total work done by these forces on the body depends only on the initial and final positions of the body in space. These forces, whose total work is path independent, are called conservative forces.
L_{A \rightarrow B}=f(A, B) \equiv f(B)-f(A) \equiv
\equiv-(U(B)-U(A))=-\Delta U
POTENTIAL ENERGY AND CONSERVATIVE FORCES
U(x)=\frac{1}{2} k x^2
F_x \Delta x=-\Delta U \Rightarrow F_x=-\frac{\Delta U}{\Delta x} \Rightarrow F_x=-\frac{d U}{d x}
F_x=-\frac{d V}{d x}=-k x
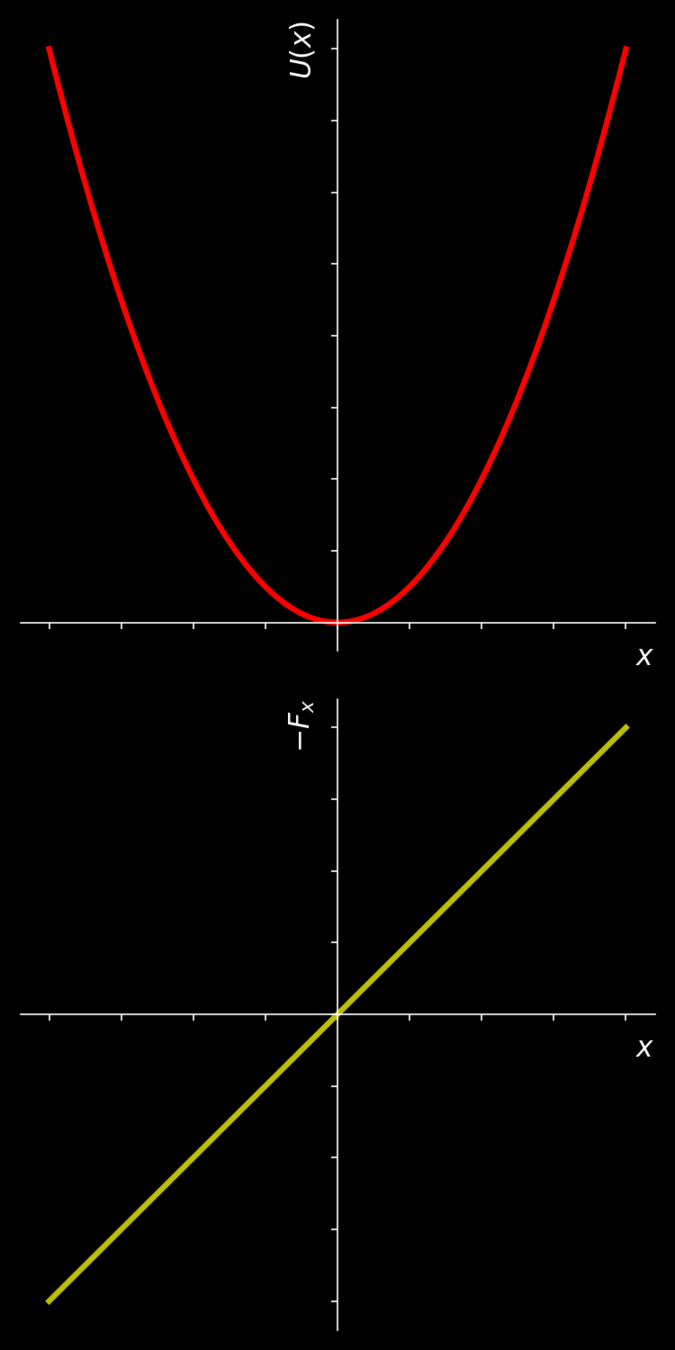
CONSERVATION OF MECHANICAL ENERGY
In presence of conservative forces, the total mechanical energy defined as E=T+U is conserved
L_{A \rightarrow B}=-\Delta U
L_{A \rightarrow B}=\Delta T
\Downarrow
\Delta T+\Delta U=0 \Rightarrow E=T+U=\text { Cost. }
HAMILTONIAN MECHANICS: WHY?
BECAUSE OF ARBITRARY REFERENCE FRAMES AND CONSTRAINTS!!!
HAMILTONIAN MECHANICS
THE HARMONIC OSCILLATOR
k_{s}
m
E = T + U
E = \frac{1}{2} m v^2 + \frac{1}{2}k_{s}(x-l)^2
H(p,x) = T(p) + U(x)
H(p,x) = \frac{p^2}{2m} + U(x)
HAMILTON'S EQUATIONS OF MOTION
HARMONIC OSCILLATOR
H(p,x) = \frac{p^2}{2m} + U(x)
\begin{cases}
\frac{\partial H}{\partial p} = \frac{dx}{dt} \\
\frac{\partial H}{\partial x} = -\frac{dp}{dt} \\
\end{cases}
k_{s}
m
HAMILTON'S EQUATIONS OF MOTION
DIATOMIC MOLECULE
H(p,x) = \frac{p_1^2}{2m} - \frac{p_2^2}{2m} + \frac{k_s}{2}(x_2-x_1-l)
\begin{cases}
\frac{\partial H}{\partial p_1} = \frac{dx_1}{dt}, \, \frac{\partial H}{\partial x_1} = -\frac{dp_1}{dt} \\
\frac{\partial H}{\partial p_2} = \frac{dx_2}{dt}, \, \frac{\partial H}{\partial x_2} = -\frac{dp_2}{dt} \\
\end{cases}
k_{s}
m
m
m
m
k_{s}
l
2l
Materials and Platforms for AI - Newtonian and Hamiltonian Mechanics
By Giovanni Pellegrini
