PHYSICS INFORMED NEURAL NETWORKS FOR TIME-INDEPENDENT QUANTUM EIGENPROBLEMS
THE PAPER

THE NETWORK
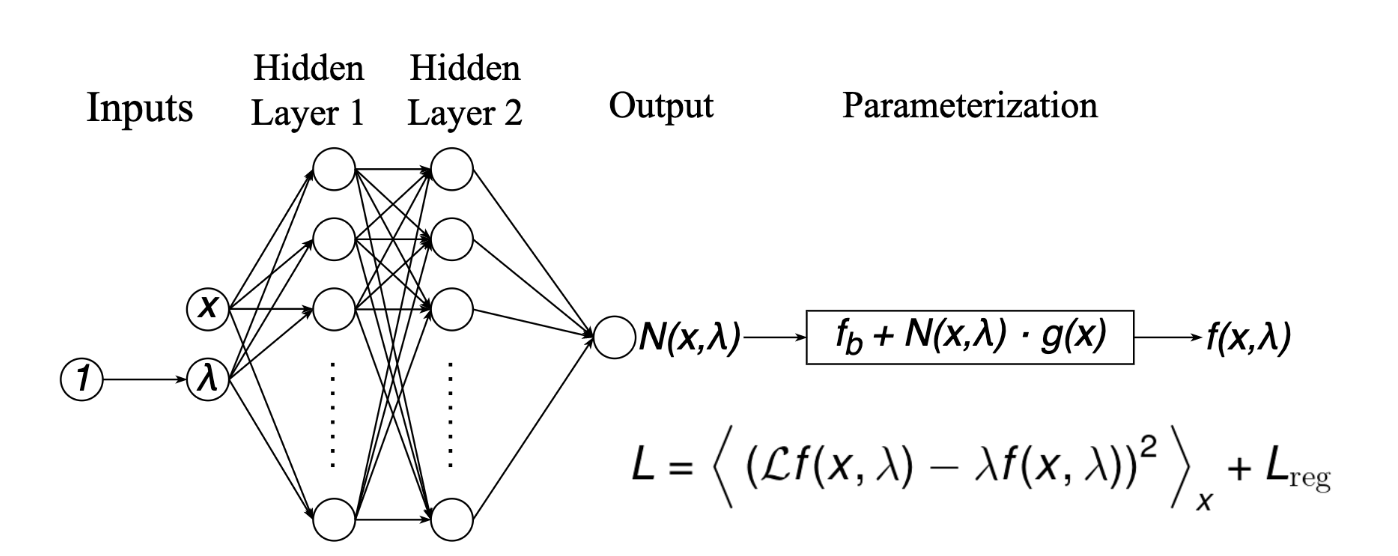
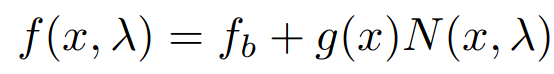
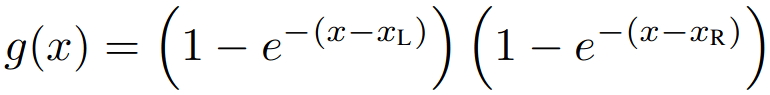
THE LOSSES
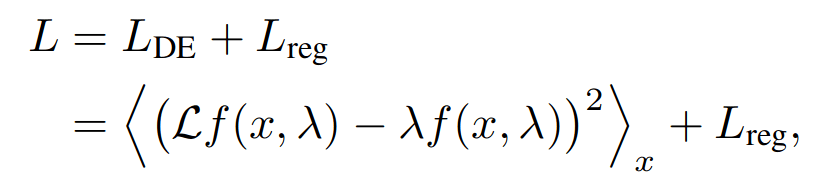
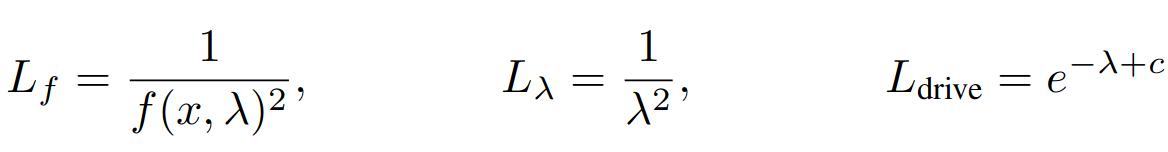
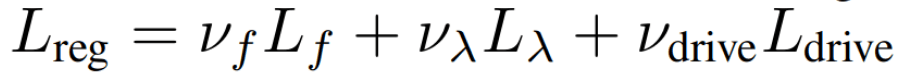
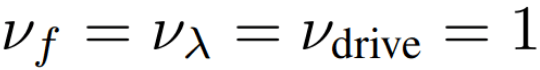
THE PROBLEM
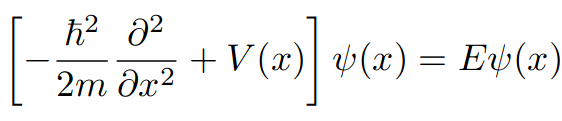
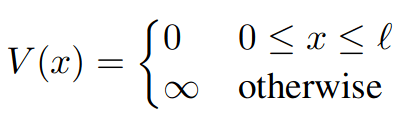
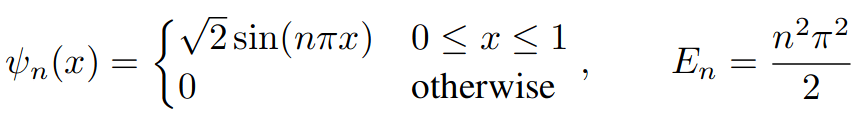
THE SOLUTION
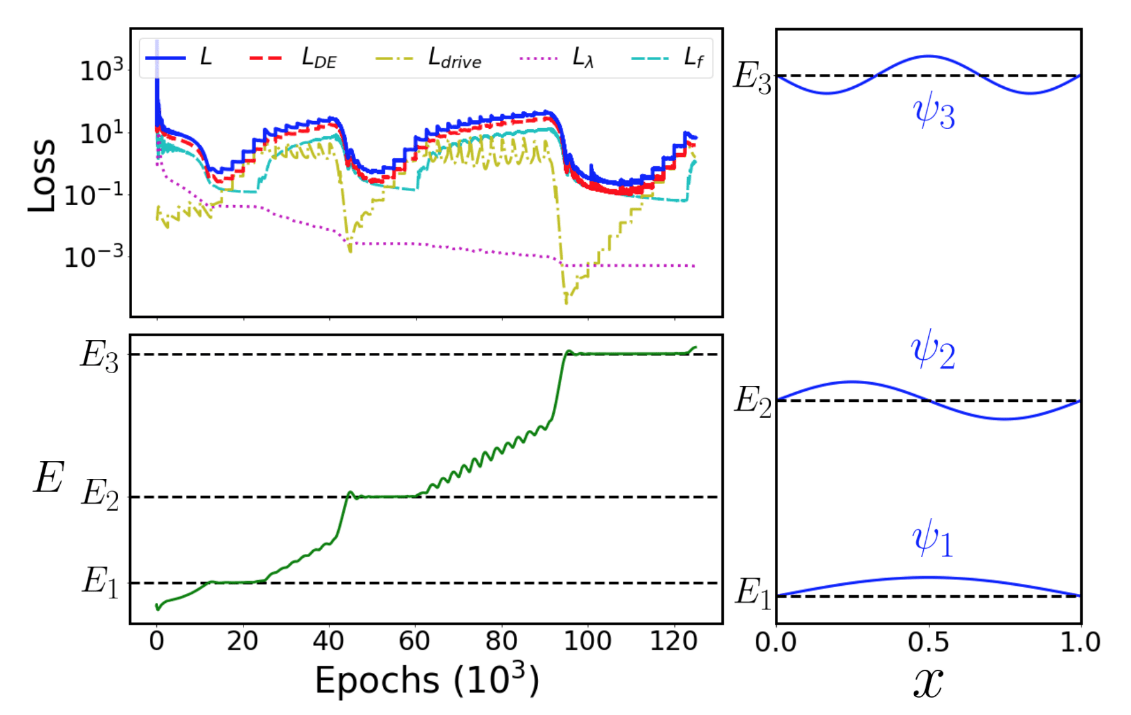
PINN 2.0 - ABOUT THE UNPHYSICAL LOSSES
L_{E_n} = \frac{1}{E_n^2}
L_{f} = \frac{1}{f(x,E_n)^2}
L_{drive} = e^{-E_n + c}
Unphysical
Promotes eigenfunctions that are not identically zero
Unphysical
Promotes eigenvalues that are not identically zero
Unphysical
Drives the discovery of new eigenvalues around \(c\)
L_{DE} = \langle \mathcal{L}f(x,E_n) - E_n f(x,E_n) \rangle
Physical
Promotes the solution of schroedinger equation
NORMALIZATION LOSS
\int_{\mathcal{All \, Space}} |\psi(x)|^2 dx = 1
L_{norm} = \bigg( \sum_{i=1}^{n_{batch}} \big[ f^*(x_i,E_n) f(x_i,E_n) \big] - \frac{n_{batch}}{x_R - x_L} \bigg)^2
def loss_norm(psi,n_batch,x_min,x_max):
"""
Calculates the normalization loss value.
Args:
psi (torch.Tensor): A tensor representing the psi values.
n_batch (int): The number of samples in the batch.
x_min (float): The minimum value in the data range.
x_max (float): The maximum value in the data range.
Returns:
torch.Tensor: The normalized loss value.
"""
# loss
loss = (torch.dot(psi.squeeze(),psi.squeeze())/n_batch - 1.0/(x_max-x_min)).pow(2)
return loss# dataset range, number of points, and points per batch
x_min, x_max, n_train = 0.0, 1.0, 50
x_tensor = torch.linspace(x_min, x_max, n_train).reshape(-1,1)
x_tensor.requires_grad = True
delta_x = x_tensor[1]-x_tensor[0]
# create dataset and dataloader
dataset = AugmentedTensorDataset(x_tensor)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=n_train, pin_memory=True, shuffle=True)
# training parameters
n_sampling = 1 # sampling metrics every n_sampling batches
# list of previous checkpoints
checkpoint_list = []
m_psi = orth_builder(checkpoint_list,x_tensor)ORTHOGONAL LOSS
\begin{dcases}
\hat{H}\psi_n = E_n \psi_n \\
\braket{\psi_n|\psi_m} = \int_{\mathcal{All \, Space}} \psi^*_n(x)\psi_m(x) dx = \delta_{mn}
\end{dcases}
\begin{dcases}
\ket{\psi_{orth}} = \sum_{n=1}^{N-1} \ket{\psi_n} \\
\braket{\psi_{orth}|\psi_N} = \sum_{n=1}^{N-1} \braket{\psi_{n}|\psi_N} = \sum_{n=1}^{N-1} \delta_{nN} = 0
\end{dcases}
L_{orth} = \braket{\psi_{orth}|\psi_N}
ORTHOGONAL LOSS
# dataset range, number of points, and points per batch
x_min, x_max, n_train = 0.0, 1.0, 50
x_tensor = torch.linspace(x_min, x_max, n_train).reshape(-1,1)
x_tensor.requires_grad = True
delta_x = x_tensor[1]-x_tensor[0]
# create dataset and dataloader
dataset = AugmentedTensorDataset(x_tensor)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=n_train, pin_memory=True, shuffle=True)
# training parameters
n_sampling = 1 # sampling metrics every n_sampling batches
# list of previous checkpoints
checkpoint_list = ['./checkpoints/best_model_E1.pt','./checkpoints/best_model_E2.pt','./checkpoints/best_model_E3.pt']
m_psi = orth_builder(checkpoint_list,x_tensor)def orth_builder(checkpoint_list,x_tensor):
"""
Builds a tensor of orthogonal psi eigenfunctions from multiple model checkpoints.
Args:
checkpoint_list (list of str): A list of paths to model checkpoints.
x_tensor (torch.Tensor): A tensor containing the input data.
Returns:
torch.Tensor: A tensor with shape (x_tensor.shape[0], len(checkpoint_list)), where each column contains the psi values for a corresponding checkpoint.
"""
if len(checkpoint_list) == 0:
m_psi = torch.zeros(x_tensor.shape[0],1)
else:
# create storage tensor
m_psi = torch.ones(x_tensor.shape[0],len(checkpoint_list))
# looping over checkpoints
for i_c, checkpoint in enumerate(checkpoint_list):
# load checkpoint
checkpoint = torch.load(checkpoint)
model.load_state_dict(checkpoint['model_state_dict'])
# evaluate model
model.eval();
out = model(x_tensor.detach())
N_x = out[0].detach()
m_psi[:,i_c] = f_x_param(x_tensor.detach(),N_x,x_min,x_max,0.0).squeeze()
return m_psiL_{orth} = \braket{\psi_{orth}|\psi_N}
# create dataset and dataloader
dataset = AugmentedTensorDataset(x_tensor)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=n_train, pin_memory=True, shuffle=True)ORTHOGONAL LOSS
def loss_orth(psi,m_psi):
"""
Calculates the orthogonal loss between a reference vector (psi) and a set of basis vectors (m_psi).
Args:
psi (torch.Tensor): A tensor of shape (batch_size, 1) representing the reference vector.
m_psi (torch.Tensor): A tensor of shape (batch_size, num_basis) representing the set of basis vectors.
Returns:
torch.Tensor: The orthogonal loss between psi and m_psi, normalized by the number of basis vectors.
"""
loss = 0.0
n_batch = m_psi.shape[0]
n_orth = m_psi.shape[1]
for i_psi in range(n_orth):
loss += torch.dot(m_psi[:,i_psi].squeeze(),psi.squeeze())/n_batch
return torch.abs(loss)/n_orthL_{orth} = \braket{\psi_{orth}|\psi_N}
FULL LOSS
# Compute the loss and its gradients
r_loss_de = loss_de(f_x,x_input,E_n)
r_loss_norm = loss_norm(f_x,n_train,x_min,x_max)
r_loss_orth = loss_orth(f_x,m_psi)
loss = r_loss_de + r_loss_norm + 0.1*r_loss_orth
loss.backward()\mathcal{Loss} = L_{DE} + L_{norm} + L_{orth}
A DIFFERENT (HARMONIC) POTENTIAL
def loss_de(psi,x,U,E_n):
"""
Computes the loss function for a differential equation.
This function calculates the loss based on the second derivative and
the energy term of a solution (`psi`) to a differential
equation. It assumes ℏ (reduced Planck constant) to be 1 and mass (m) to be 1.
Args:
psi (torch.Tensor): The solution tensor of shape (batch_size, ...).
x (torch.Tensor): The independent variable tensor of shape (batch_size, ...).
U (torch.Tensor): The potential energy term tensor of shape (batch_size, ...).
E_n (torch.Tensor): The energy term tensor of shape (batch_size, ...).
Returns:
torch.Tensor: The loss value as a scalar, representing the mean squared
error of the calculated loss across the batch.
"""
# compute the second derivative of the solution
dpsi_dx = df_dx(psi,x)
d2psi_dx2 = df_dx(dpsi_dx,x)
# compute the loss for ℏ=1 and m=1
loss = (d2psi_dx2/2 + (E_n-U)*psi)/E_n
loss = (loss.pow(2)).mean();
return lossdef harmonic_potential(x_tensor,k=4):
"""
Calculates the harmonic potential energy for a given tensor.
Args:
x_tensor (torch.Tensor): A tensor representing the position(s) in the potential.
k (float, optional): The force constant of the harmonic potential. Defaults to 4.0.
Returns:
torch.Tensor: The harmonic potential energy for the given positions.
"""
U = 0.5*k*x_tensor.pow(2)
return U\begin{dcases}
U(x) = \frac{1}{2} k x^2 \\[8pt]
\psi_n(x) = \frac{1}{\sqrt{2^n n!}} \frac{e^{-\frac{x^2}{2}}}{\pi^{1/4}} H_{n}(x) \\[8pt]
E_n = n+\frac{1}{2}
\end{dcases}
A DIFFERENT (HARMONIC) POTENTIAL
# enumerating through the dataloader
for i, x_input in enumerate(dataloader):
# Zero your gradients for every batch!
optimizer.zero_grad()
# Make predictions for this batch
N_x, E_n = model(x_input)
# parametrizing the solution
f_x = f_x_param(x_input, N_x, x_min, x_max, 0.0)
# compute the potential
U = harmonic_potential(x_input)
# Compute the loss and its gradients
r_loss_de = loss_de(f_x,x_input,U,E_n)
r_loss_norm = loss_norm(f_x,n_train,x_min,x_max)
r_loss_orth = loss_orth(f_x,m_psi)
loss = r_loss_de + r_loss_norm + 0.1*r_loss_orth
loss.backward()# dataset range, number of points, and points per batch
x_min, x_max, n_train = -6, 6, 50
x_tensor = torch.linspace(x_min, x_max, n_train).reshape(-1,1)
x_tensor.requires_grad = True
delta_x = x_tensor[1]-x_tensor[0]Boundary Conditions
\( \psi(-6) = \psi(6) = 0 \)
Modified training step
Materials and Platforms for AI - Physics Informed Neural Networks for Quantum Eigenproblems
By Giovanni Pellegrini
Materials and Platforms for AI - Physics Informed Neural Networks for Quantum Eigenproblems
- 168



