elettricità
cariche, campi, potenziale e corrente
L'AMBRA E L'IDEA DI CARICA ELETTRICA
- Osserviamo un'interazione a distanza, senza necessità di contatto
- L'interazione può essere sia attrattiva sia repulsiva
- La stessa azione su oggetti diversi genera effetti diversi
l'elettroscopio di volta
cariche, isolanti e conduttori
conduttori ed isolanti


conduttori
isolanti
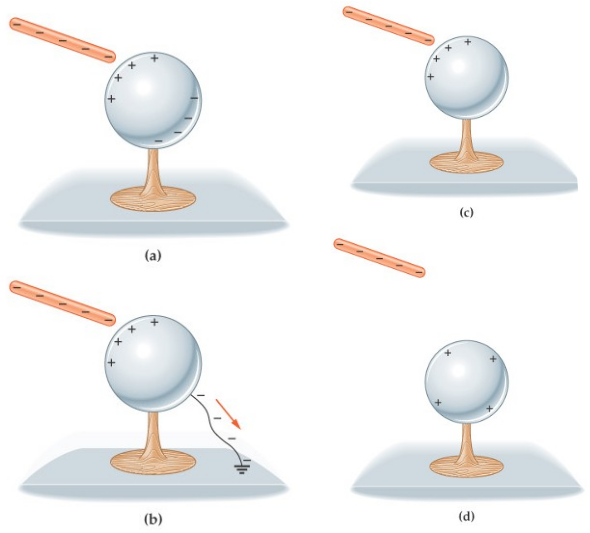
carica per induzione di un conduttore
LEGGE DI COULOMB
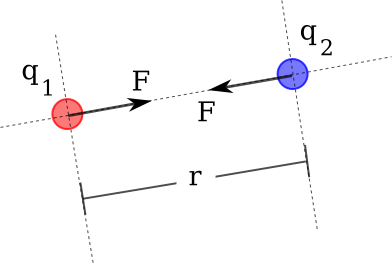
\[ F_{\mathrm{el}} = k \frac{q_{1}q_{2}}{r^{2}}; \; k = \frac{1}{4 \pi \varepsilon_{0}} \]
\[ F_{\mathrm{el}} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1}q_{2}}{r^{2}} \]
\[ q \Rightarrow Coulomb \, [C] \]
\[ e = 1.6 \cdot 10^{-19} (C) \]
campo elettrico

\[ \vec{F}_{\mathrm{el}} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{0}q}{r^{2}} \vec{u}_{r} \]
\[ \vec{E} = \frac{\vec{F}_{\mathrm{el}}}{q_{0}} = \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{r^{2}} \vec{u}_{r} \]
linee di forza del campo elettrico: 1
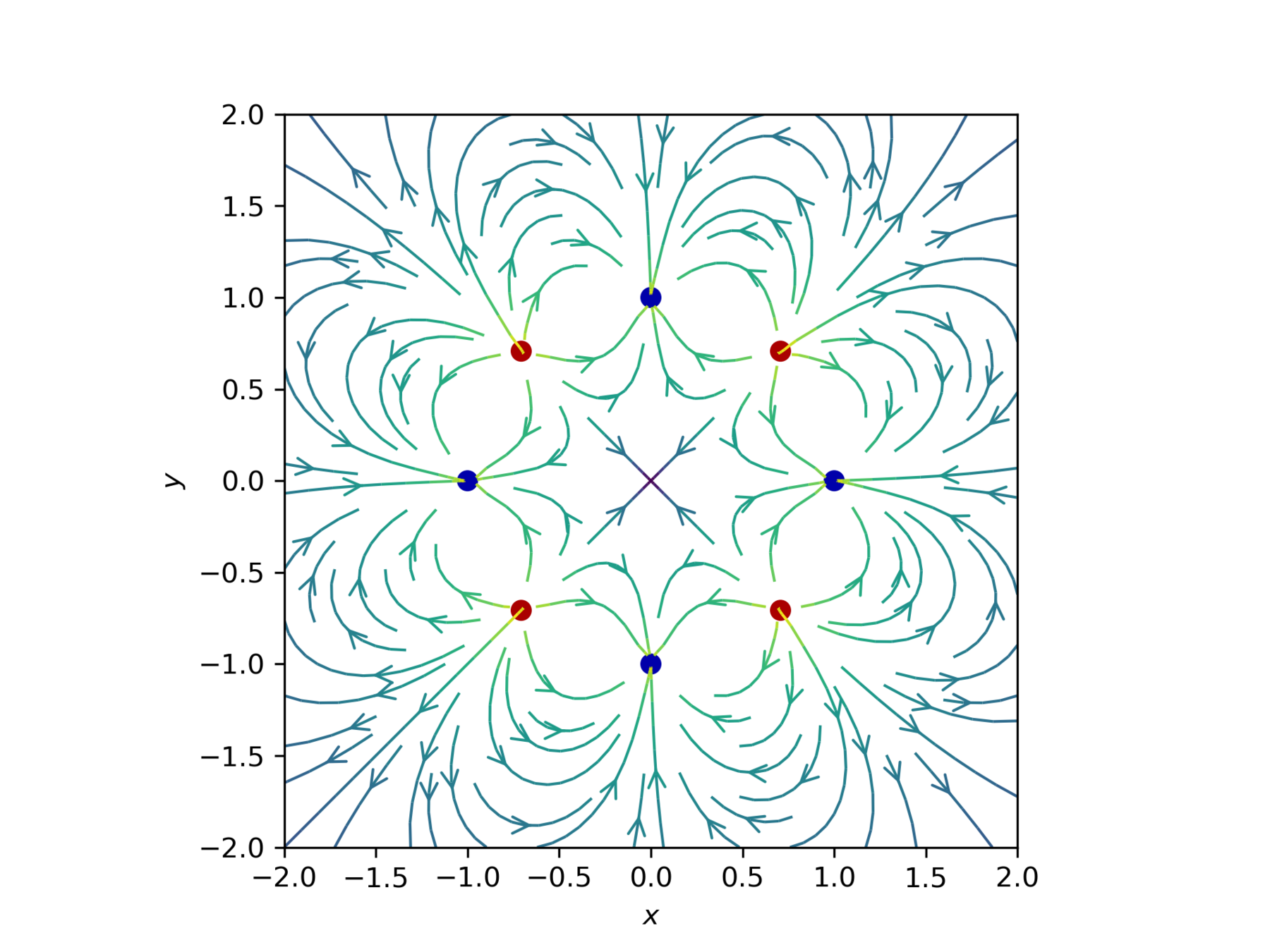
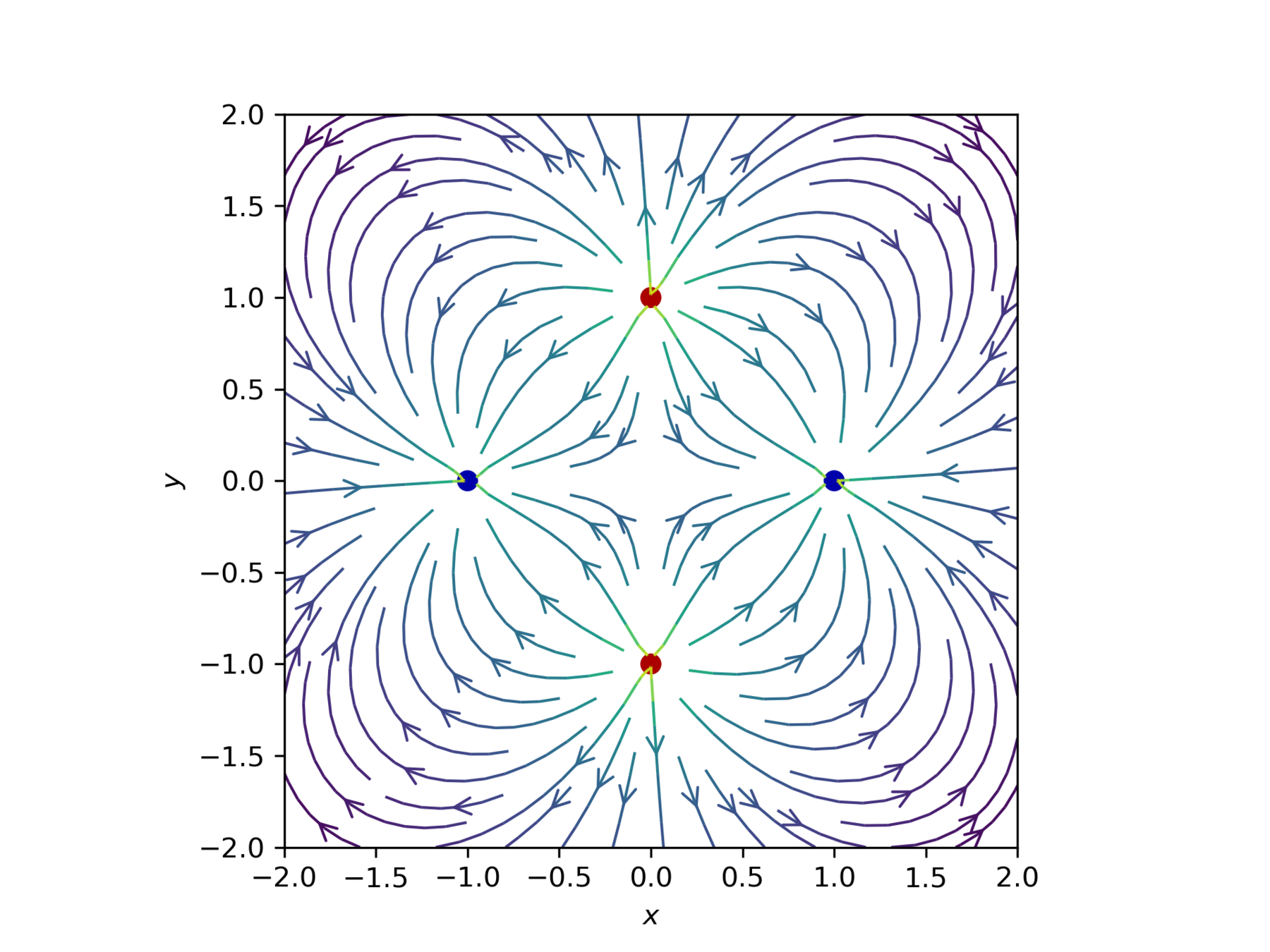
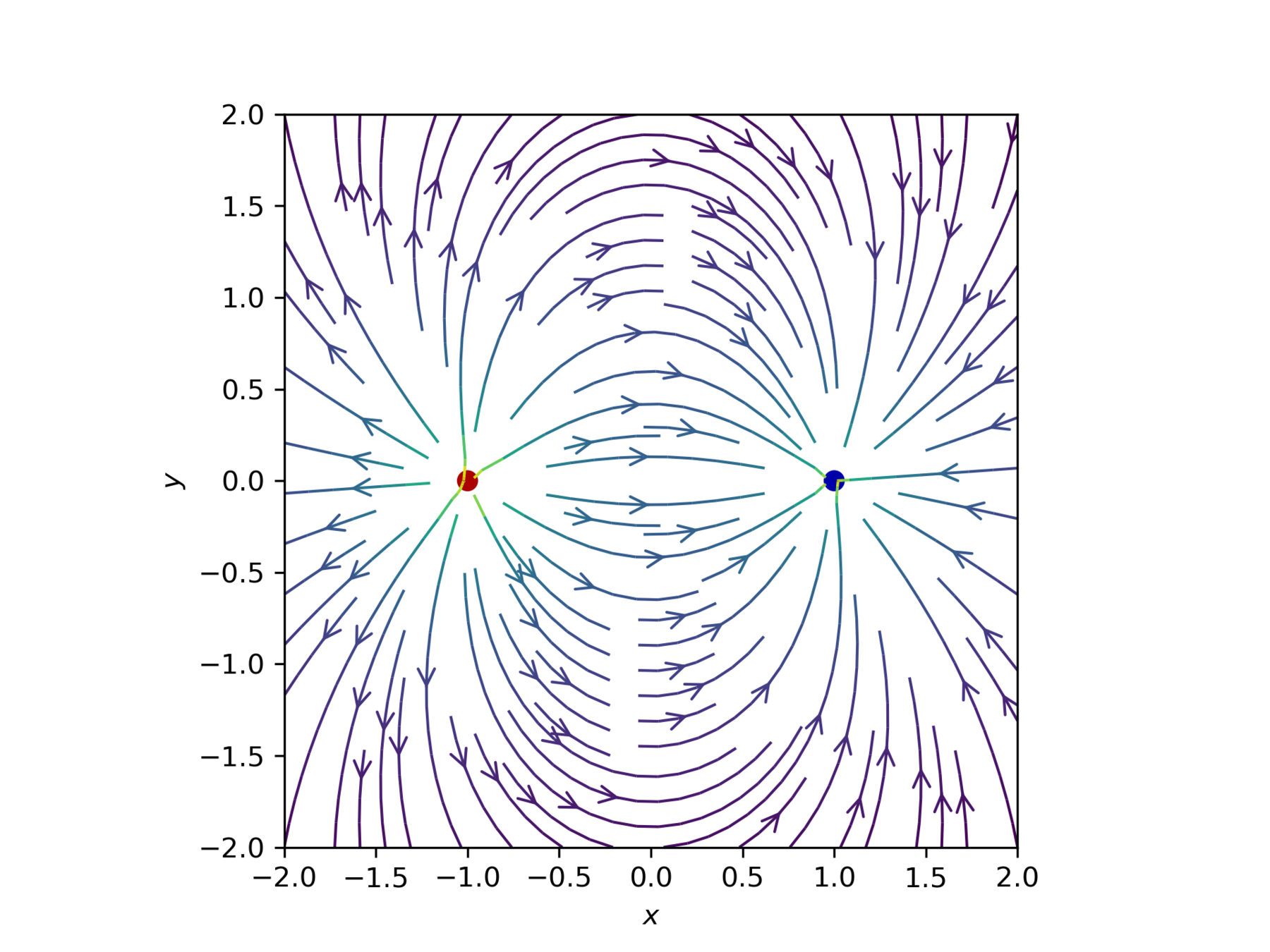
dipolo elettrico
quadrupolo elettrico
ottupolo elettrico
linee di forza del campo elettrico: 2
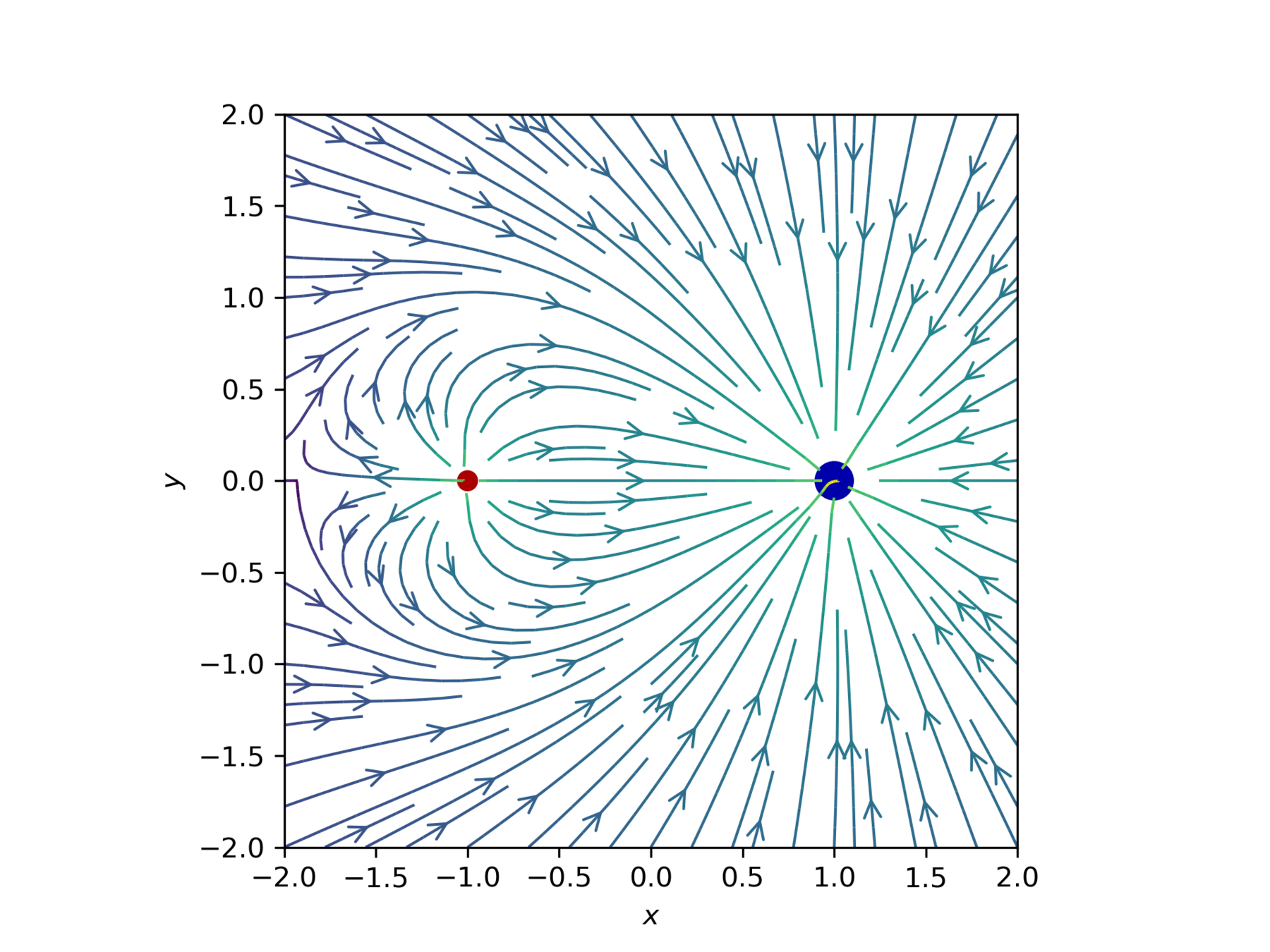

dipolo simmetrico
dipolo asimmetrico
linee di forza del campo elettrico: 3


piano carico
sfere cariche
moto in un campo elettrico tra due armature cariche

\[ | \vec{E} | \approx costante \]
\[ \vec{a} = \frac{\vec{F}}{m} = \frac{q \vec{E}}{m} \]
dipolo elettrico
dipolo elettrico
moto in un campo elettrico tra due armature cariche
flusso di un campo vettoriale
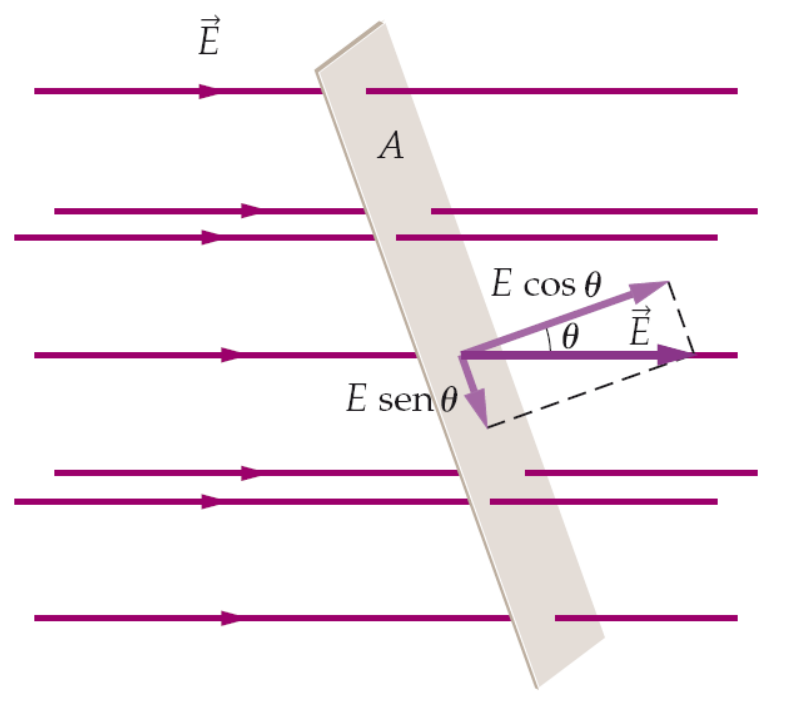
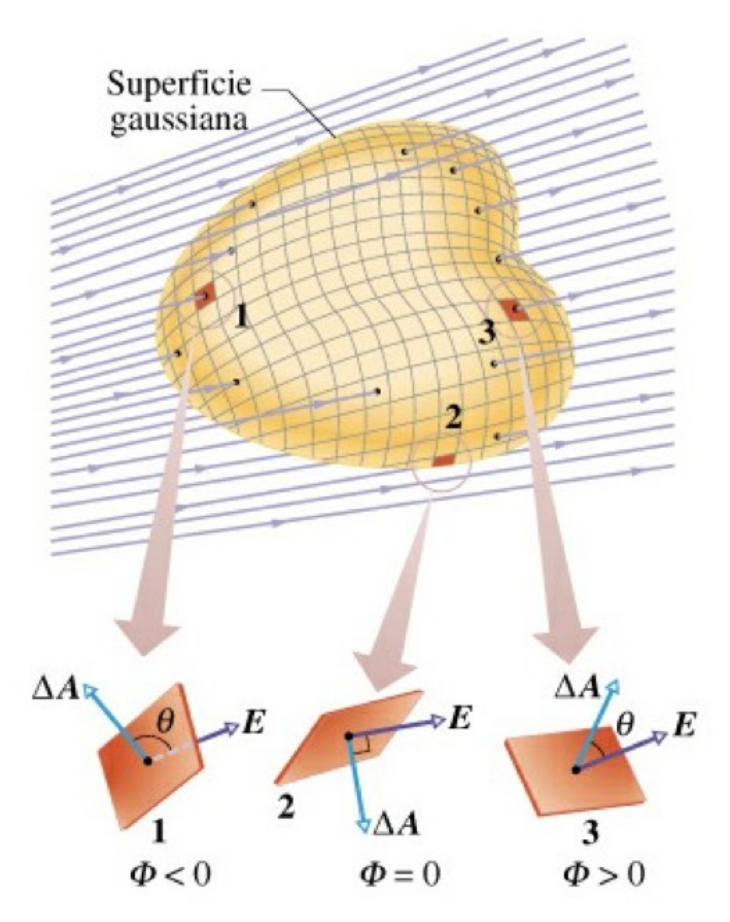
\[ \Phi = \vec{E} \cdot \vec{A} = E \, A \, cos(\theta) \]
\[ \Phi = \sum_{i} \vec{E}_{i} \cdot \Delta \vec{A}_{i} \Rightarrow \Phi = \int_{A} \vec{E} \cdot d\vec{A} \]
teorema di gauss

"Il flusso del campo elettrico attraverso una superficie chiusa è proporzionale alla carica racchiusa al suo interno"
\[ \Phi_{E} = \int_{A} \vec{E} \cdot d\vec{A} = \frac{q_{tot}}{\varepsilon_{0}} \]
esempi di utilizzo del teorema di gauss



energia potenziale e potenziale elettrostatico
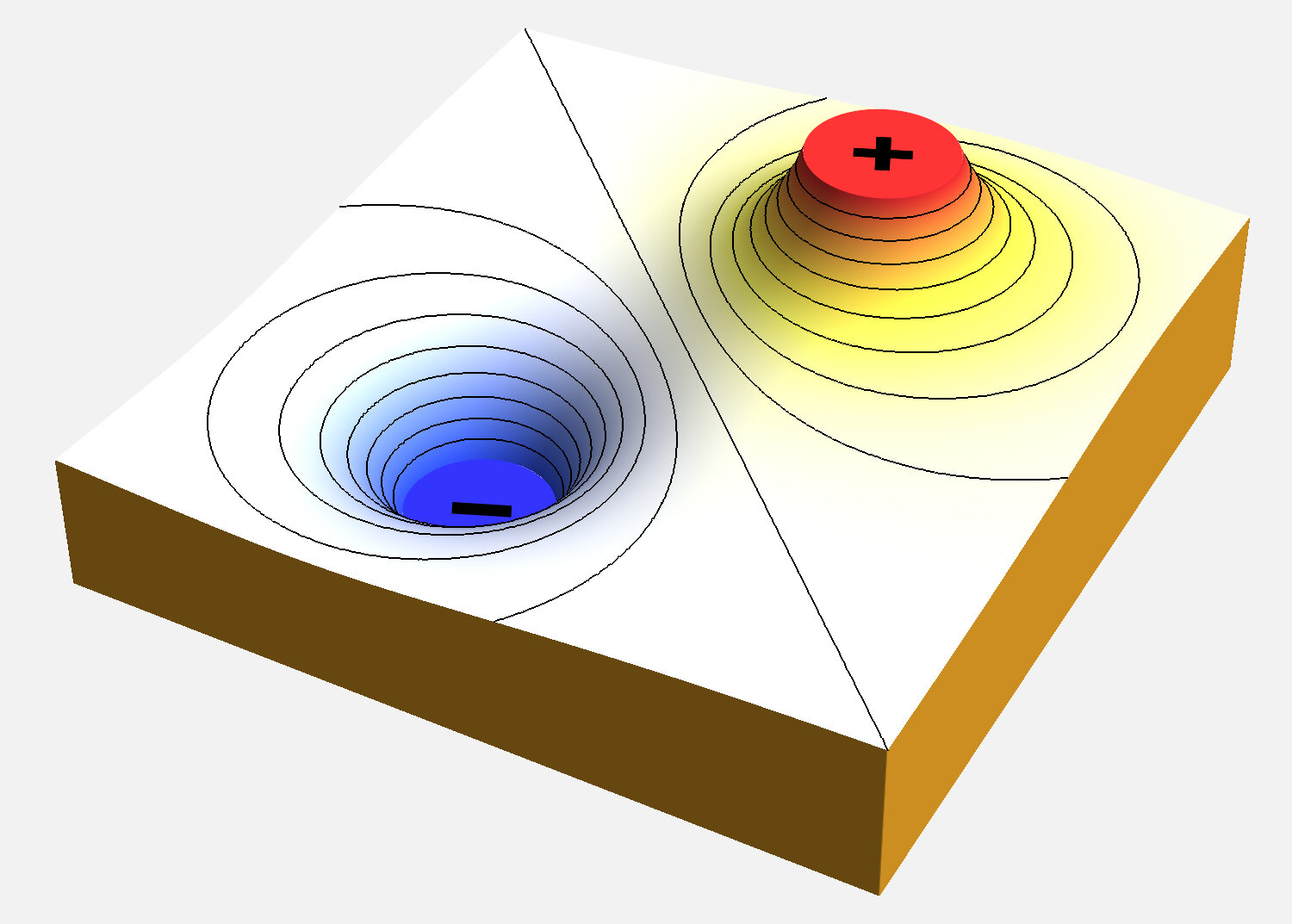
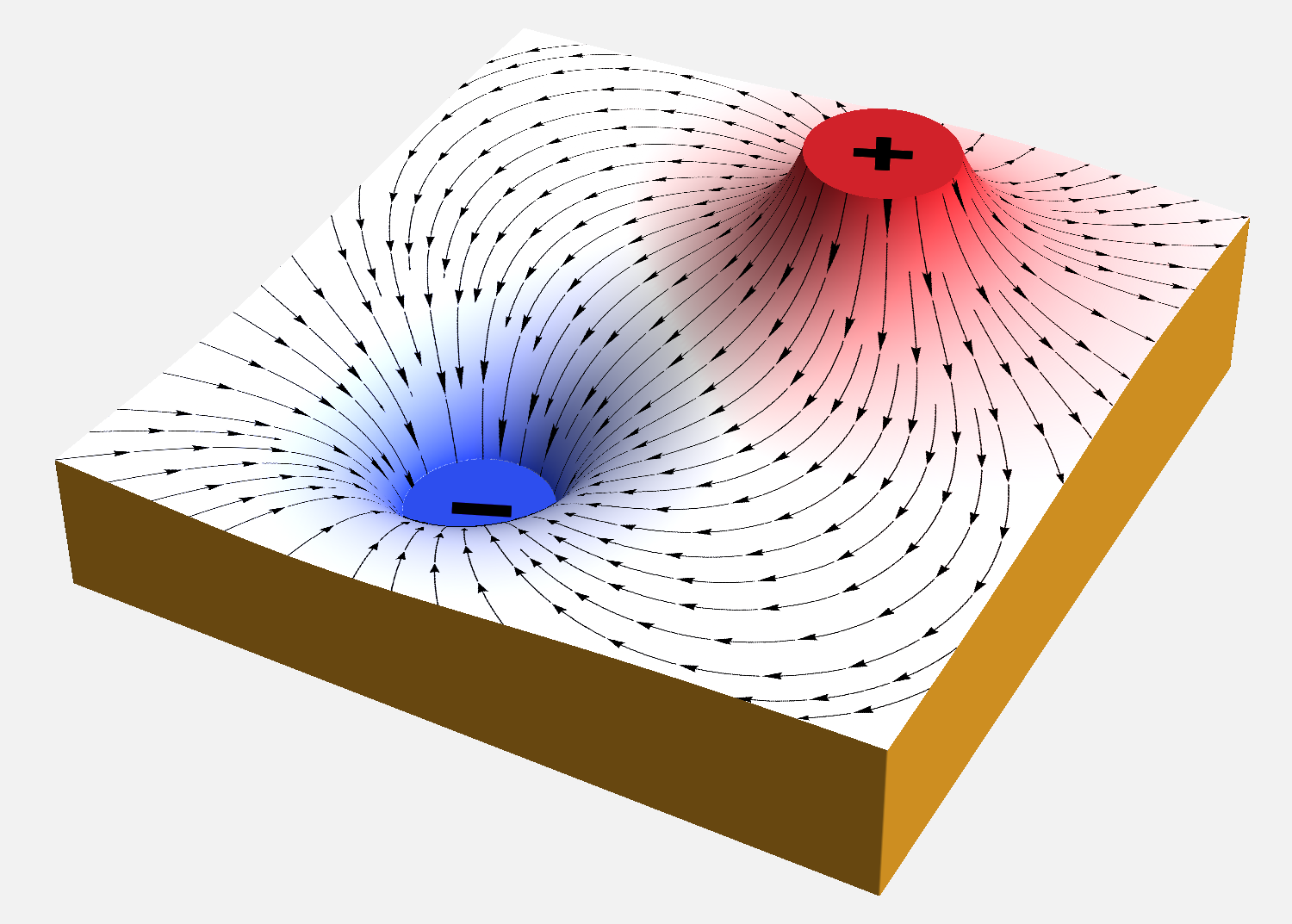
"La forza elettrostatica è una forza conservativa, quindi il suo lavoro può essere espresso tramite una variazione di energia potenziale"
\[ L^{el}_{A \to B} = \int_{A}^{B} \vec{F}_{el} \cdot d \vec{s} = -(U_{e}(B) - U_{e}(A)) = - \Delta U_{e} \]
\[ \frac{L^{el}_{A \to B}}{q} = \int_{A}^{B}\vec{E}_{el} \cdot d \vec{s} = -(V(B) - V(A)) = - \Delta V \]
\[ \Delta U_{e}= q \Delta V \]
\[ U_{e} \to [J] \; \Rightarrow \; V \to \left[ \frac{J}{C} \right] ;\; [Volt] \]
potenziale di una carica positiva
potenziale di una carica negativa
POTENZIALE DI UNA DISTRIBUZIONE DI CARICHE
proprietà dei conduttori carichi

"All'equilibrio, il campo elettrico all'interno di un conduttore carico è nullo. Di conseguenza l'eccesso di cariche presenti è confinato alla superficie."
"All'equilibrio un conduttore è una superficie equipotenziale"
proprietà dei conduttori carichi
"La capacità mette in relazione la carica accumulata su un conduttore in relazione al suo potenziale"

\[ C = \frac{Q}{V} \; \; \; [F] \]
\[ U_{e} = \frac{1}{2} \frac{Q^{2}}{C} = \frac{1}{2} Q V \]
CONDENSATORI IN SERIE ED IN PARALLELO

corrente elettrica
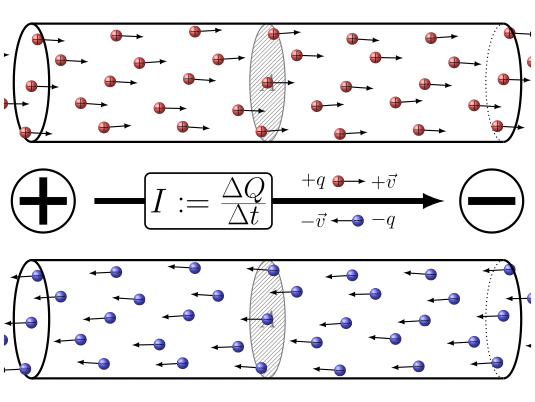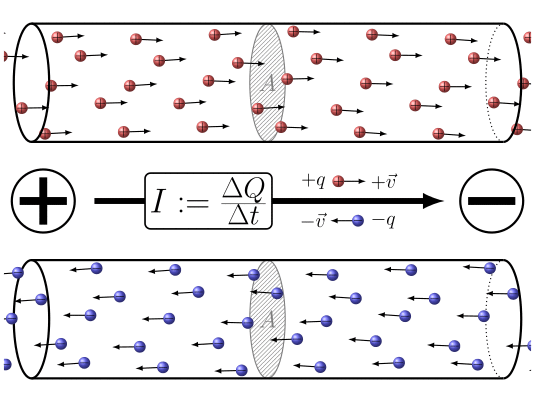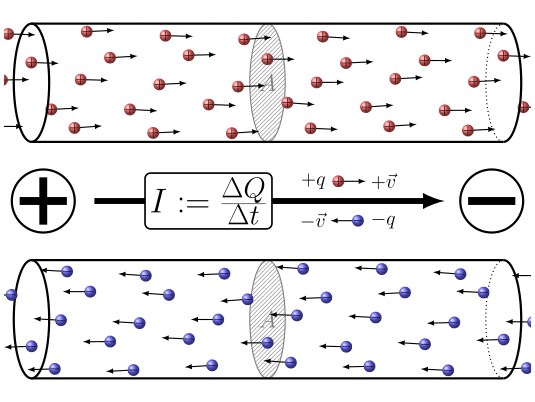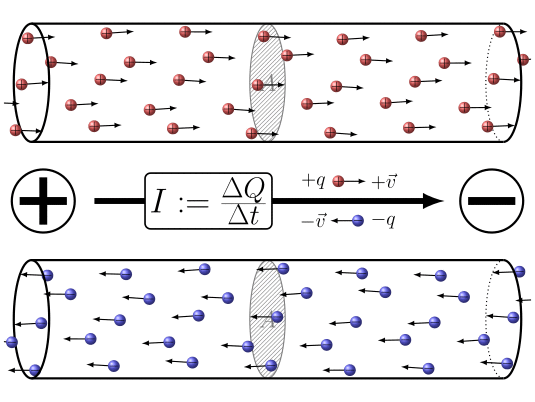
"La corrente elettrica è un moto ordinato di cariche elettriche"
\[ I = \lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t} = \frac{dq}{dt} = Corrente \]
\[ Ampere \, [A] \Rightarrow \left[ \frac{C}{s} \right] \]
corrente elettrica: interpretazione microscopica

\[ I = q \,n \, A \, v_{d} \]
- \( q = carica \, del \, portatore \, [C] \)
- \( n = cariche \, libere \, per \, unità \, di \, volume \, [m^{-3}] \)
- \( A = sezione \, del \, conduttore \, [m^{2}] \)
- \( v_{d} = velocità \, di \, deriva \, [m/s]; \, v_{d} \propto \Delta V \)
\[ J = \frac{I}{A} = q \, n \, v_{d} = Densit \grave{a} \, di \, corrente \]
resistenza, resistività e legge di ohm

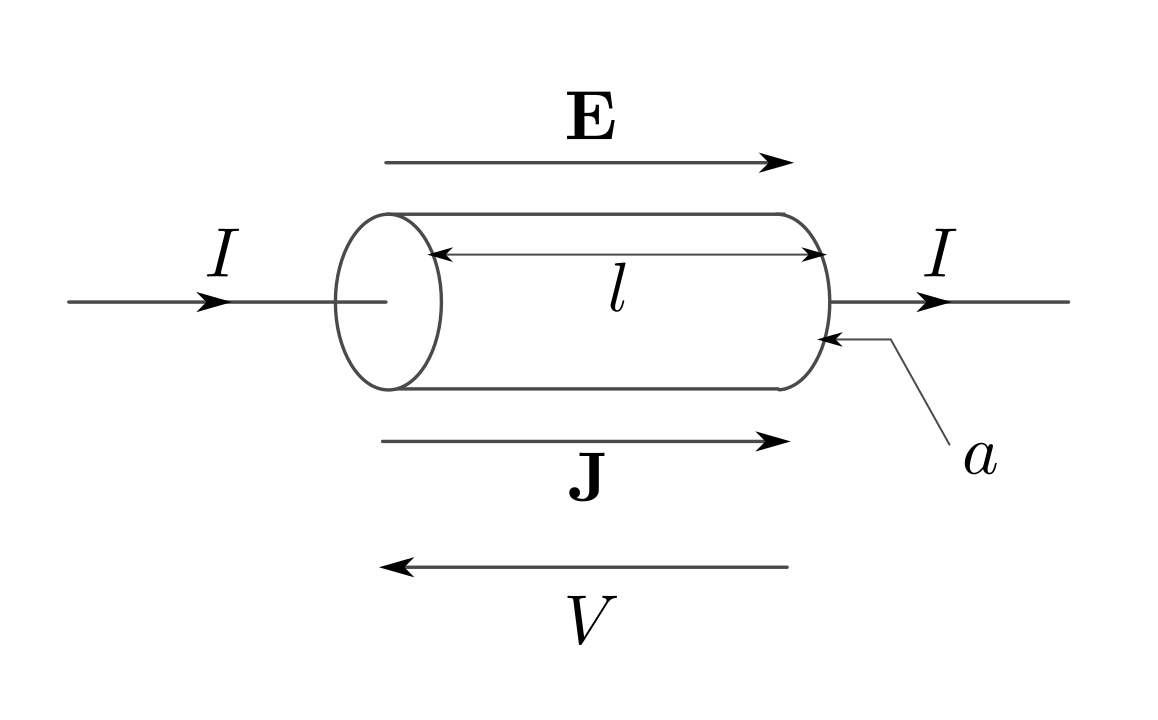
\[ V = I \, R \]
\[ R = \rho \frac{L}{A} \]
\( R = resistenza \Rightarrow Ohm \, [\Omega] = \left[ \frac{V}{A} \right] \)
\( \rho = resistività \Rightarrow \left[ \frac{\Omega}{m} \right] \)
resistenze in parallelo
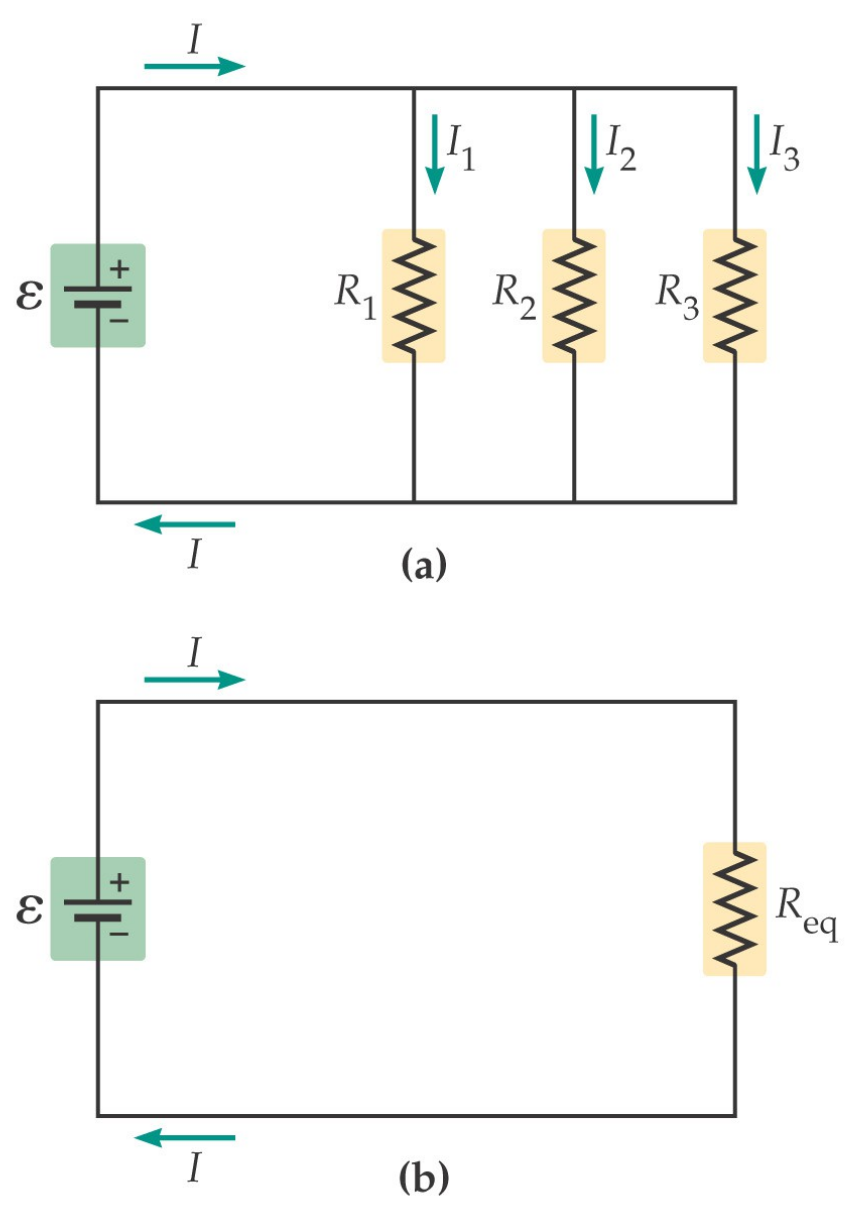
\[ \frac{1}{R_{eq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \]
\[ R_{eq}<R_{1} \]
\[ R_{eq}<R_{2} \]
\[ R_{eq}<R_{3} \]
resistenze in serie
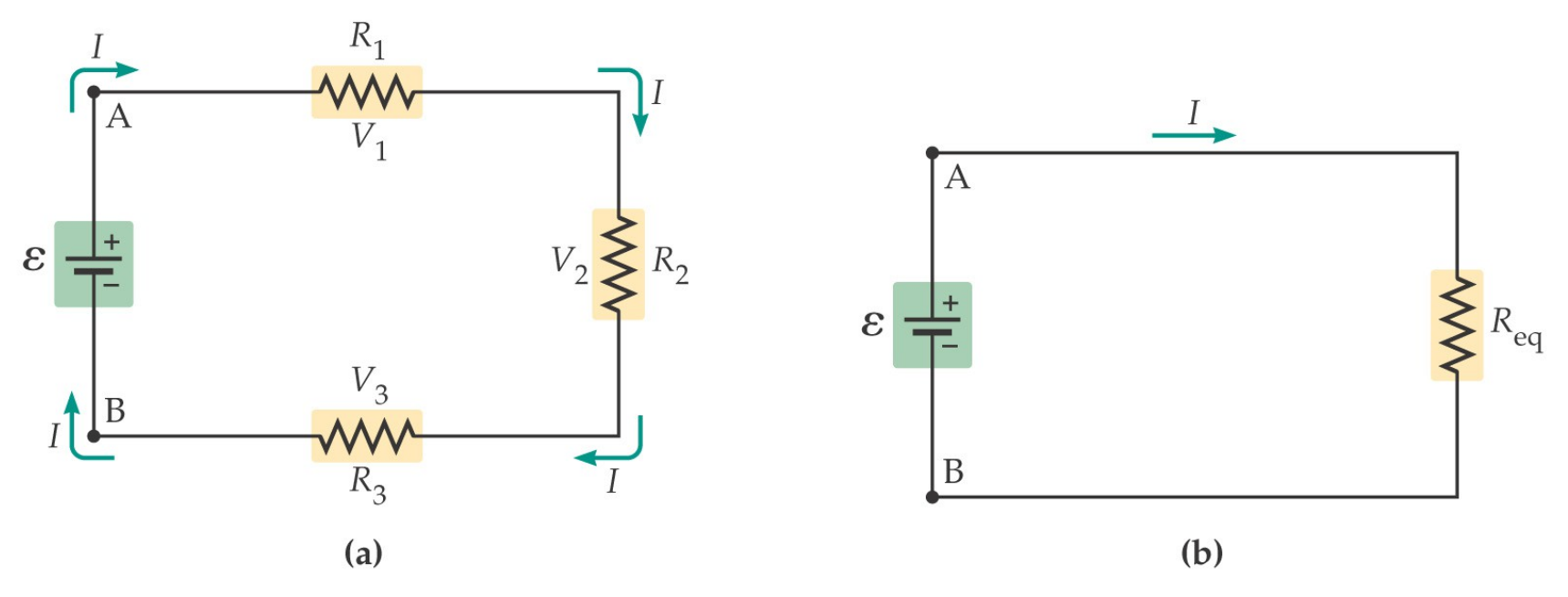
\[ R_{eq} = R_{1} + R_{2} + R_{3} \]
Musicologia: elettricità
By Giovanni Pellegrini
Musicologia: elettricità
- 66



