lavoro ed energia
lavoro di una forza costante
lungo un percorso rettilineo
\bullet \; L=\vec{F} \cdot \vec{s} = F \cdot x \cdot cos(\theta)
\bullet \; Joule \Rightarrow [Kg \cdot m^{2} \cdot s^{-2}]
lavoro: caso generale
\bullet \; \Delta L_{1} = \vec{F}_{1} \cdot \Delta \vec{s}_{1}
\bullet \; \Delta L_{2} = \vec{F}_{2} \cdot \Delta \vec{s}_{2}
\bullet \; \ldots
\bullet \; \ldots
\bullet \; \Delta L_{n} = \vec{F}_{n} \cdot \Delta \vec{s}_{n}
L=\lim _{\Delta s \rightarrow 0} \sum_i \vec{F}_i \cdot \Delta \vec{s}_1=\int_1^2 \vec{F} \cdot d \vec{s}
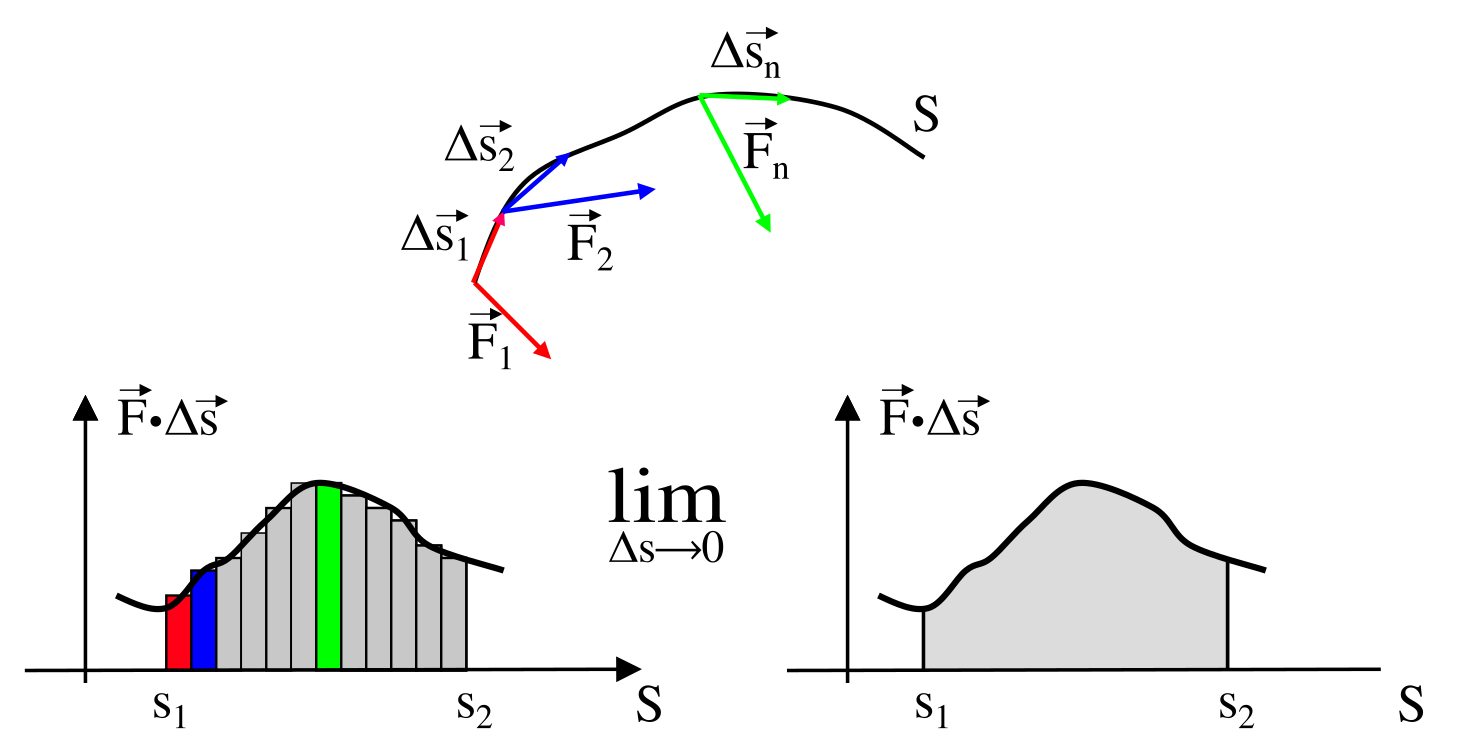
lavoro: forze conservative
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(3)}
L_{A \rightarrow B}^{(2)}
=
=
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(n)} + L_{B \rightarrow A}^{(m)} = 0
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(3)}
L_{A \rightarrow B}^{(2)}
\neq
\neq
L_{A \rightarrow B}^{(1)}
L_{A \rightarrow B}^{(n)} + L_{B \rightarrow A}^{(m)} \neq 0
Forze conservative
Forze non conservative
forze conservative: forza elastica
L_{A \rightarrow B}^{(n)} = L_{A \rightarrow B}^{(m)} = L_{A \rightarrow B}^{(l)}
L_{A \rightarrow B}^{(n)} = -\frac{1}{2}k(x^{2}_{B}-x^{2}_{A})
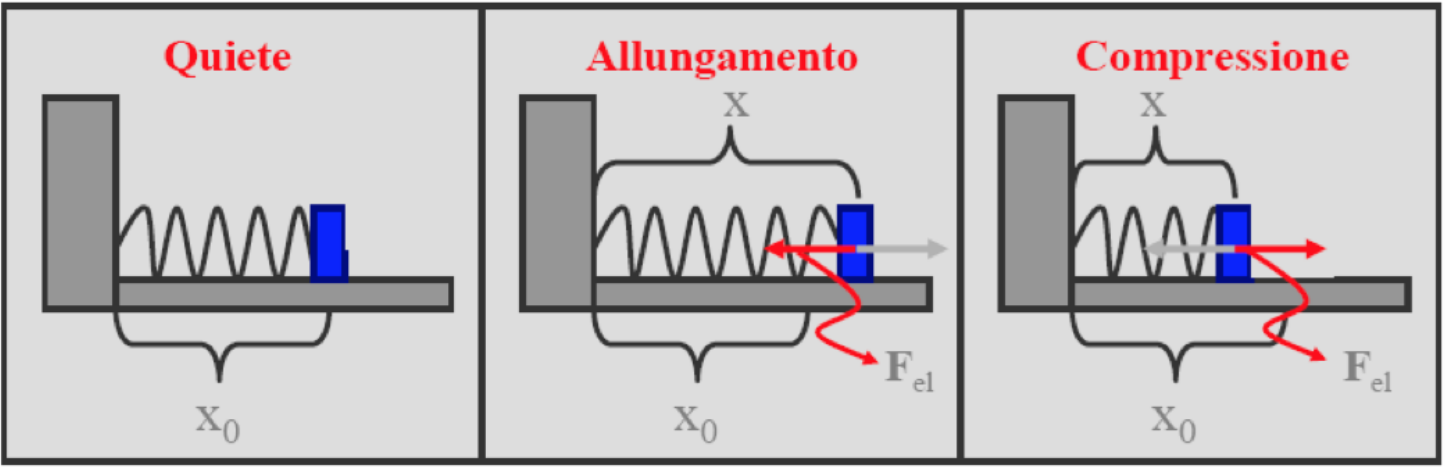
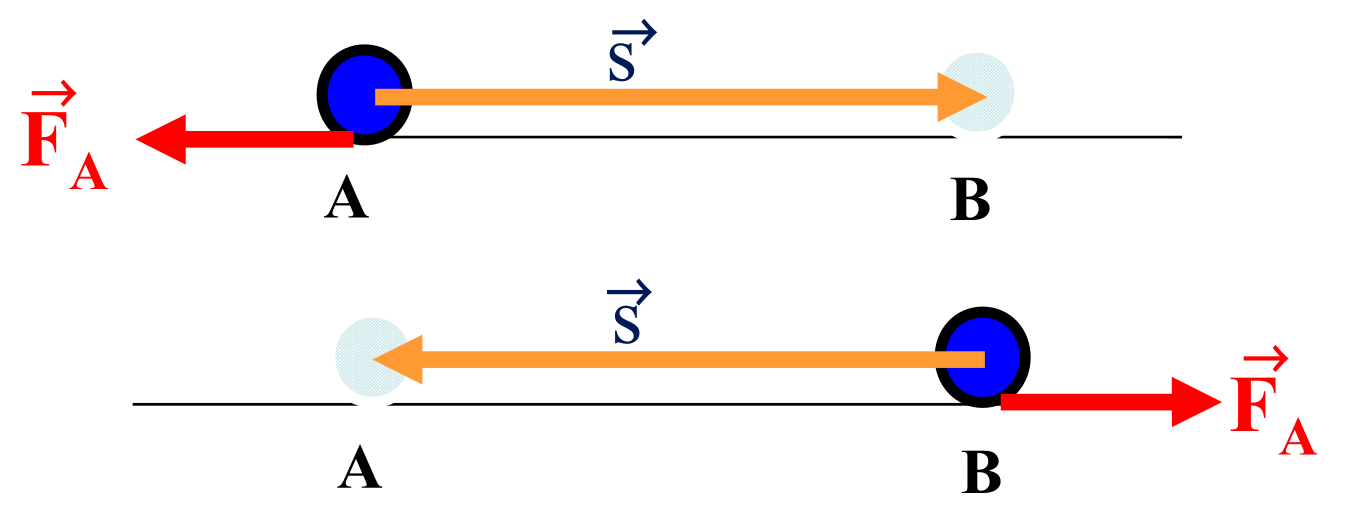
forze non conservative
attrito dinamico
L_{A \rightarrow B}^{(n)} + L_{B \rightarrow A}^{(m)} \neq 0
L_{A \rightarrow B} + L_{B \rightarrow A} = -2 \cdot F_{\mu_{d}} \cdot s
il concetto di energia
L'energia è la capacità (potenziale) di compiere lavoro, e con esso condivide la stessa unità di misura (J)
Forme di energia
- Cinetica
- Potenziale gravitazionale
- Potenziale elastica
- Potenziale elettrica
- Termica
- Chimica
- Nucleare
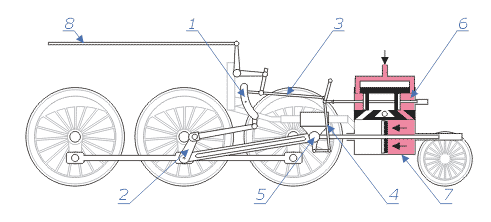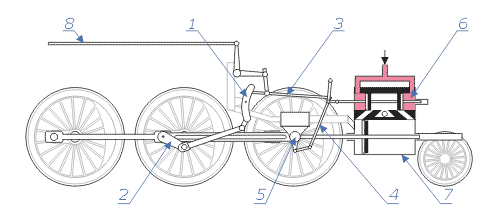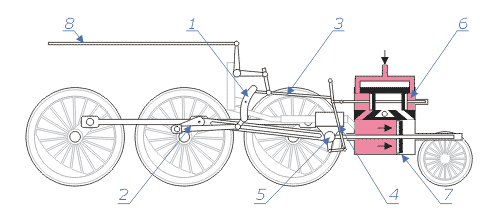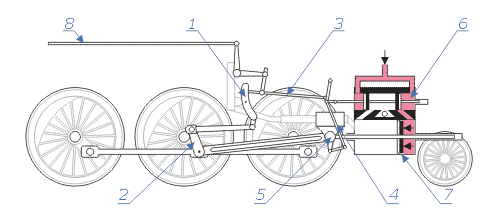
principio di conservazione dell'energia
La variazione della quantità totale di energia in un sistema isolato è nulla
Se in un sistema l'energia sembra non conservarsi, ciò è spesso dovuto alla presenza di una forza dissipativa (ad esempio l'attrito), ed in tal caso l'energia viene convertita in calore.
\Delta E_{tot}=0
E_{tot}=cost
energia cinetica
L'energia cinetica di un corpo è associata al suo stato di movimento, ossia alla sua velocità
T = \frac{1}{2}mv^{2}
Teorema dell'energia cinetica
L = \Delta T = \frac{1}{2}m(v^{2}_{f}-v^{2}_{i})
energia potenziale
Per forze conservative, il lavoro è unicamente funzione dei punti di partenza e di arrivo, e pertanto può essere espresso tramite la funzione energia potenziale U
L_{A \rightarrow B}=f(A, B) \equiv f(B)-f(A) \equiv
\equiv-(U(B)-U(A))=-\Delta U
ENERGIA POTENZIALE VS FORZE CONSERVATIVE
U(x)=\frac{1}{2} k x^2
F_x \Delta x=-\Delta U \Rightarrow F_x=-\frac{\Delta U}{\Delta x} \Rightarrow F_x=-\frac{d U}{d x}
F_x=-\frac{d U}{d x}=-k x
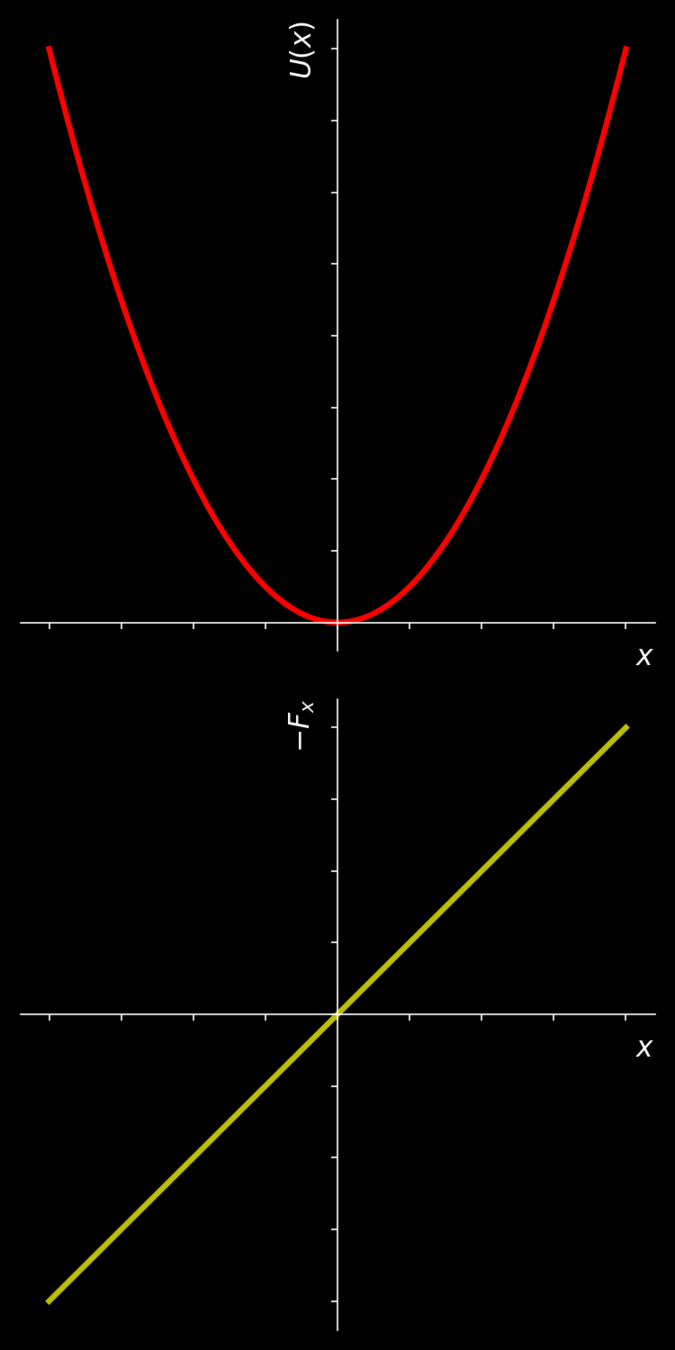
conservazione dell'energia meccanica
Se tutte le forze che agiscono su un corpo sono conservative, allora la sua energia meccanica definita come E=T+U si conserva
L_{A \rightarrow B}=-\Delta U \\
L_{A \rightarrow B}=\Delta T
\Downarrow
\Delta T+\Delta U=0 \Rightarrow E=T+U=\text { Cost. }
potenza e potenza meccanica
W_m=\frac{\Delta L}{\Delta t} \Rightarrow W=\lim _{\Delta t \rightarrow 0} \frac{\Delta L}{\Delta t}=\frac{d L}{d t} \; (W a t t, J / s)
W=\frac{dL}{d t} = \frac{d[\vec{F} \cdot \vec{s}]}{dt}= \vec{F} \cdot \frac{d\vec{s}}{dt} = \vec{F} \cdot \vec{v}
potenza media e istantanea
potenza meccanica
Musicologia: lavoro ed energia
By Giovanni Pellegrini
