Seminar kognitive Modellierung:
Parameterschätzung I
Jan Göttmann, M.Sc.
Fahrplan
| Datum | Thema |
|---|---|
| 25.10.2023 | Organisation und Ablauf |
| 08.11.2023 | Einführung: Grundlagen der Modellierung |
| 15.11.2023 | Einführung II: Grundlagen der Modellierung |
| 22.11.2023 | Parameterschätzung I: Diskrepanzfunktionen & Schätzalgorithmen |
| 29.11.2023 | Parameterschätzung II: Maximum Likelihood & Beyond |
| 06.12.2023 | Parameterschätzung III: Hands On in R Parameter Estimation |
| 13.12.2023 | Multinomial Processing Tree Models (Theorie) |
| 20.12.2023 | Anwendung von MPT Modellen (R-Sitzung) |
| 10.01.2024 | Drift Diffusion Models (Theorie) |
| 17.01.2024 | Drift Diffusion Models (Anwendung) |
| 24.01.2023 | Mixture Models (Theorie) |
| 31.01.2024 | Mixture Models (Anwendung) |
| 07.02.2024 | Puffersitzung |
Einführung II: Recap
-
Parameter sind interne Modellvariablen, die das Verhalten eines Modells beeinflussen (Tuning Knobs)
-
Freie Parameter die werden auf Grundlage der beobachteten Daten geschätzt
-
Fixe Parameter skalieren die Schätzung der freien Parameter. Freie Parameter können fixiert werden, um das Modell sparsamer zu machen.
-
Parameter können in die gleiche psychologische Bedeutung in unterschiedlichen Modellarchitekturen haben – sie bestimmen nicht die Architektur, sondern das Modellverhalten !
Einführung II: Recap
-
… werden aus den Daten geschätzt, um die Modellpassung zu maximieren (Tuning Knobs)
-
…bestimmen (zum Teil) die Sparsamkeit des Modells
-
…erhöhen die Flexibilität (und Komplexität) des Modells
Freie Parameter..
-
… werden nicht geschätzt
-
…haben wenig Einfluss auf die Sparsamkeit des Modells (außer ein freier Parameter wird „fixiert“)
Fixierte Parameter..
Parameterschätzung I: Einführung
Experiment
Mensch
Daten
Modell
Vorhersagen
Parameter
Diskrepanzfunktion
Parameterschätzung I: Einführung
Experiment
Mensch
Daten
Modell
Vorhersagen
Diskrepanzfunktion durch
anpassen der freien Parameter „minimieren“
Parameterschätzung I: Einführung
Diskrepanzfunktionen (Cost Functions, Error Functions)
\mathcal{L}_{\text{ML}}(\theta) = -\frac{1}{N} \sum_{i=1}^{N} \log P(y_i | x_i, \theta)
\mathcal{L}_{\text{MSE}}(\theta) = \frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i, \theta))^2
\mathcal{L}_{\text{RMSE}}(\theta) = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i, \theta))^2}
\mathcal{L}_{\text{MAE}}(\theta) = \frac{1}{N} \sum_{i=1}^{N} |y_i - f(x_i, \theta)|
\mathcal{L}_{\text{CE}}(\theta) = -\frac{1}{N} \sum_{i=1}^{N} y_i \log(f(x_i, \theta)) + \\ (1-y_i) \log(1 - f(x_i, \theta))
Parameterschätzung I: Einführung
-
Der Fit zwischen den empirischen Daten und den Vorhersagen eines Modells wird durch eine Diskrepanzfunktion ermittelt
-
Es gibt viele verschiedene Diskrepanzfunktionen mit unterschiedlichen statistischen Vor- und Nachteilen!
-
Diskrepanzfunktionen drücken den Fit eines Modells in der Abweichung der Vorhersagen von den empirischen Daten aus
-
Die Diskrepanzfunktion wird in der Parameterschätzung schrittweise minimiert, bis die beste „Lösung“ - also die minimalste Abweichung gefunden ist
Diskrepanzfunktionen (Cost Functions, Error Functions)
\mathcal{L}_{\text{ML}}(\theta) = -\frac{1}{N} \sum_{i=1}^{N} \log P(y_i | x_i, \theta)
\mathcal{L}_{\text{MSE}}(\theta) = \frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i, \theta))^2
\mathcal{L}_{\text{RMSE}}(\theta) = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - f(y_i, \theta))^2}
\mathcal{L}_{\text{MAE}}(\theta) = \frac{1}{N} \sum_{i=1}^{N} |y_i - f(x_i, \theta)|
\mathcal{L}_{\text{CE}}(\theta) = -\frac{1}{N} \sum_{i=1}^{N} y_i \log(f(x_i, \theta)) + \\ (1-y_i) \log(1 - f(x_i, \theta))
Parameterschätzung I: Einführung
Diskrepanzfunktionen (Cost Functions, Error Functions)
\mathcal{L}_{\text{RMSE}}(\theta) = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - f(y_i, \theta))^2}
-
In einer Diskrepanzfunktion werden Daten und Vorhersagen gematched und die Abweichung wird berechnet
-
Diskrepanzfunktionen drücken diese Abweichung ein einer einzelnen, kontinuierlichen Zahl aus
-
Eine der bekanntesten Diskrepanzfunktion ist die „Root Mean Squared Deviation“ – RMSD:
Parameterschätzung I: Einführung
Diskrepanzfunktionen (Cost Functions, Error Functions)
-
In einer Diskrepanzfunktion werden Daten und Vorhersagen gematched und die Abweichung wird berechnet
-
Diskrepanzfunktionen drücken diese Abweichung ein einer einzelnen, kontinuierlichen Zahl aus
-
Eine der bekanntesten Diskrepanzfunktion ist die „Root Mean Squared Deviation“ – RMSD:
\mathcal{L}_{\text{RMSE}}(\theta) = \sqrt\frac{{\sum_{i=1}^{N} (y_i - f(x_i, \theta))^2}}{N}
Die mittleren Abweichungsquadrate werden berechnet!
Parameterschätzung I: Einführung
Diskrepanzfunktionen (Cost Functions, Error Functions)
-
In einer Diskrepanzfunktion werden Daten und Vorhersagen gematched und die Abweichung wird berechnet
-
Diskrepanzfunktionen drücken diese Abweichung ein einer einzelnen, kontinuierlichen Zahl aus
-
Eine der bekanntesten Diskrepanzfunktion ist die „Root Mean Squared Deviation“ – RMSD:
\mathcal{L}_{\text{RMSE}}(\theta) = \sqrt\frac{{\sum_{i=1}^{N} (y_i - f(x_i, \theta(\alpha, \beta))^2}}{N}
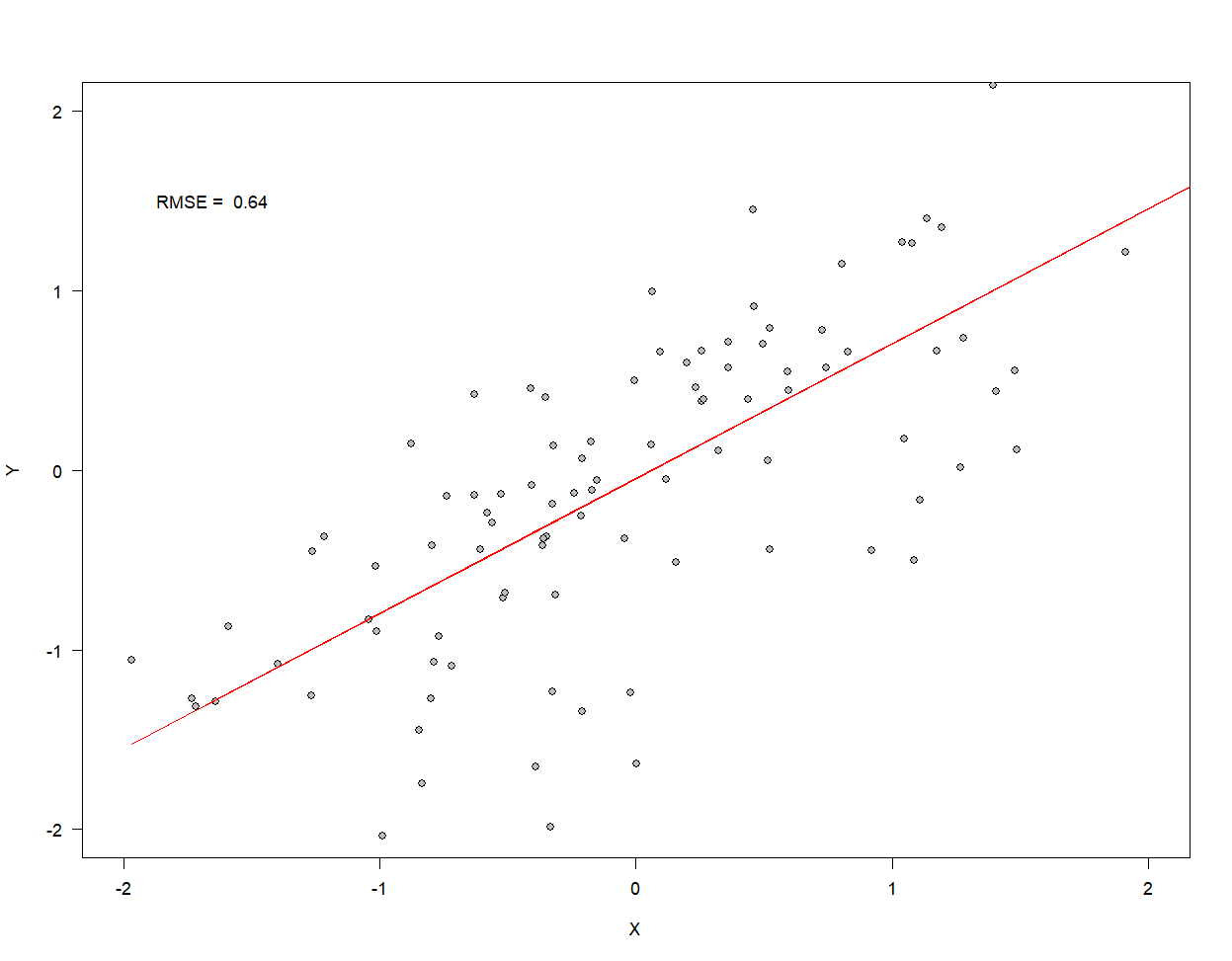
Beispiel: Einfache lineare
Regression
Parameterschätzung I: Einführung
Diskrepanzfunktionen (Cost Functions, Error Functions)
-
Die Wahl der Diskrepanzfunktion ist unabhängig von der Schätzmethode
-
Die gezeigte Regressionslinie ist jene lineare Funktion, deren Slope und Intercept die Daten nach der RMSE am besten beschreibt
-
Aber der RMSE hat keine statistischen Eigenschaften
-
… man kann keine Aussagen über die relative Evidenz von einem Modell über ein anderes Treffen
-
…Keine Annahmen von Verteilungen – gut für erste Versuche
-
Keine Basis für Modellvergleiche, Konfidenzintervalle etc.
-
Maximum Likelihood Schätzer haben alle diese Eigenschaften!
Parameterschätzung I: Einführung
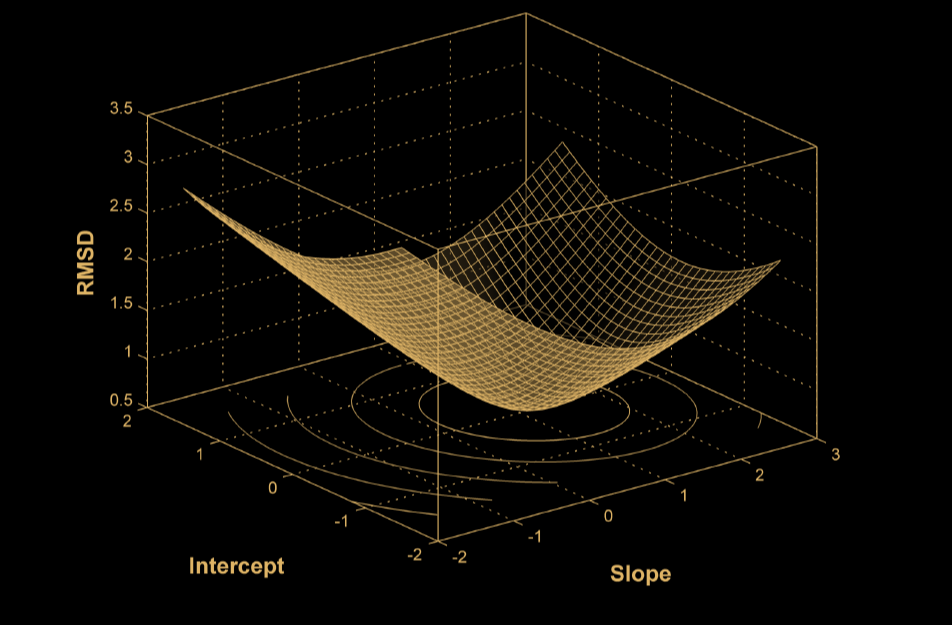
Parameter Space
Error Surface
Parameterschätzung I: Einführung
- Schrittweise Bewegung durch Parameter-Space
- Entlang des Error-Surfaces
- Bis ein (oder das) Minimum erreicht ist !
Parameter Schätzung
Aber: Wie findet man
dieses Minimum?
Parameterschätzung I: Einführung
Parameterschätzung I: Einführung
- Mit Hilfe von Schätz-Algorithmen können globale Minima – also das Gesamtminimum der gewählten Diskrepanzfunktion geschätzt werden
- Viele Algorithmen verfügbar, wir konzentrieren uns auf Simplex (Nelder-Mead-Algorithmus)
- Simplex ist ein geometrischer Algorithmus, dessen Prinzipien aber sehr einfach zu verstehen sind !
Mit Hilfe von Schätzalgorhitmen !
Parameterschätzung I: Einführung
- Ein Simplex ist eine geometrische Figur aus d+1 -Punkten, wobei d für die Dimensionalität steht:
- 2D = 3 Punkte = Dreieck
- 3D = 4 Punkte = Pyramide
- 4D = 5 Punkte = Pentachoron
- Die Dimensionalität in SIMPLEX entspricht in der Parameterschätzung der Anzahl der Parameter
SIMPLEX
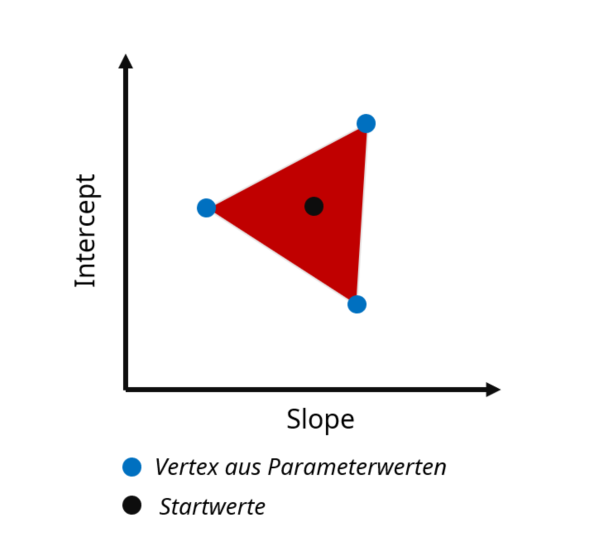
Im Beispiel unserer Linearen Regression mit 2 Parametern also ein Simplex mit 3 Dimensionen = Dreieck !
Parameterschätzung I: Einführung
- Der erste Simplex wird mit drei Parameter-Sets um einen Startpunkt herum gebildet – Diskrepanzfunktion wird initial evaluiert
- Nun „taumelt“ das Simplex den Error-Surface hinunter
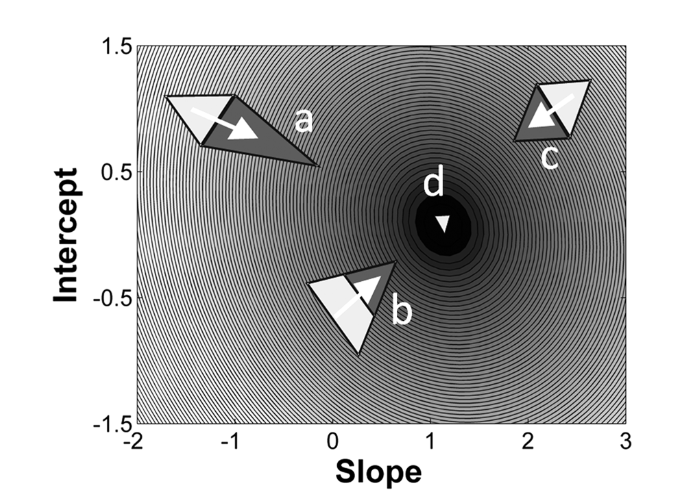
- Purzelbäume hin zum Vertex mit dem besten Fit („Reflection“) - c
- Wenn der Fit sich dadurch stark verbessert kann das auch mit einer Ausweitung („Expansion“) einhergehen ! - a
- Punkte mit dem schlechtesten Fit bewegen sich mehr Richtung Zentrum des Simplex („contraction“) - b
SIMPLEX für 2-Parameter Slope & Intercept Modell
Parameterschätzung I: Einführung
SIMPLEX für 2-Parameter Slope & Intercept Modell
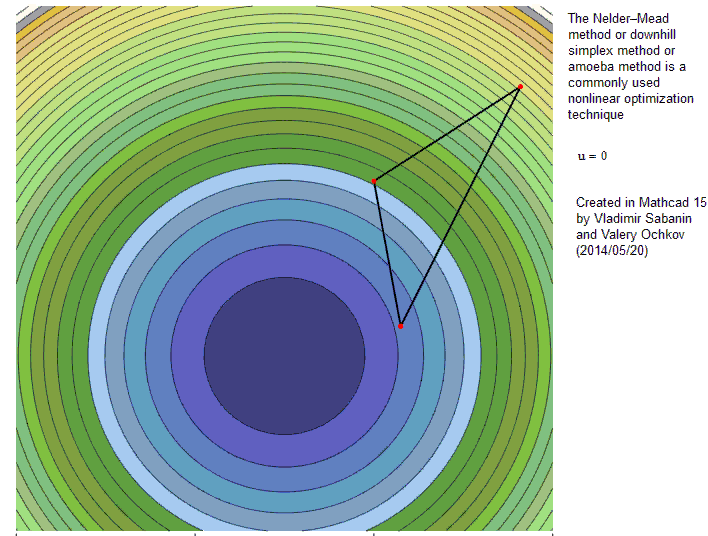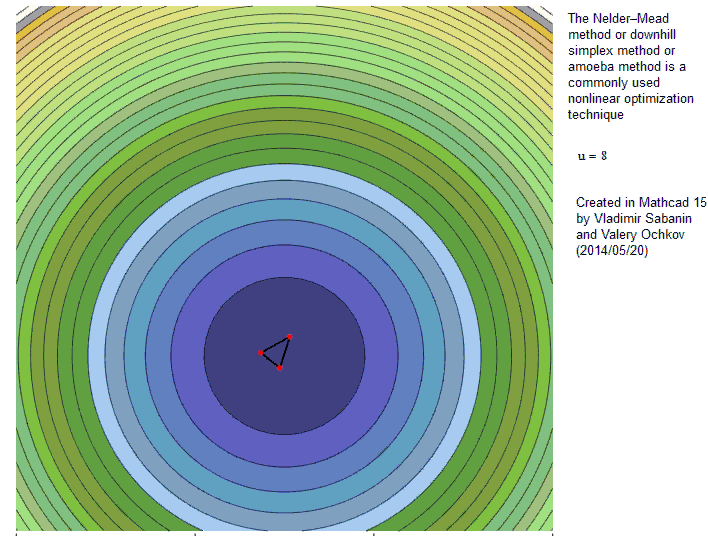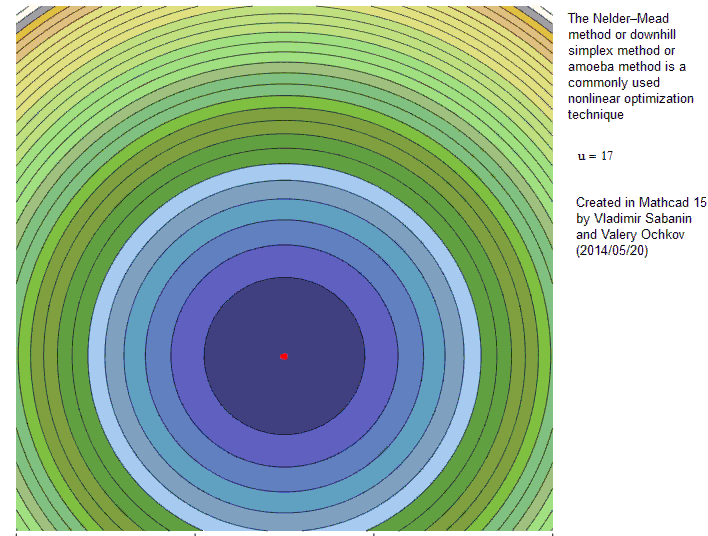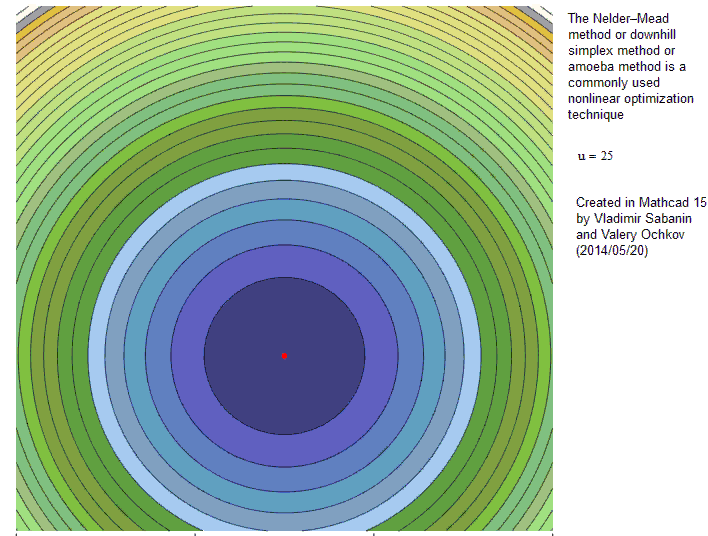
- Der erste Simplex wird mit drei Parameter-Sets um einen Startpunkt herum gebildet – Diskrepanzfunktion wird initial evaluiert
- Nun „taumelt“ das Simplex den Error-Surface hinunter
- Purzelbäume hin zum Vertex mit dem besten Fit („Reflection“) - c
- Wenn der Fit sich dadurch stark verbessert kann das auch mit einer Ausweitung („Expansion“) einhergehen ! - a
- Punkte mit dem schlechtesten Fit bewegen sich mehr Richtung Zentrum des Simplex („contraction“) - b
Parameterschätzung I: Einführung
-
Sollte nicht bei mehr als 5 Parametern genutzt werden !
-
Die Diskrepanzfunktion muss deterministisch auf die Parameterwerte bezogen sein
-
SIMPLEX (und andere verwandte Techniken) können nur „downhill“ gehen
-
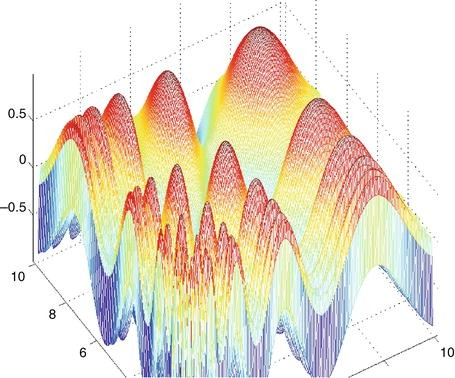
SIMPLEX ist blind für lokale Minima, das ist problematisch wenn der Error-Surface eine schwierige Form hat:
- Gräben
- Bergrücken
- Plateaus
SIMPLEX: Limitationen
-
Multiple Startwerte
- Konvergenz zu denselben bestmöglichen Parametern deutet auf ein globales Minimum hin
- vor allem, bei breiter Range der Startwerte
-
Simulated Annealing Algorithm
- „Shaking“ SIMPLEX auf Steroiden
- kann aus lokalen Minima herausspringen
SIMPLEX: Lösungen
Parameterschätzung I: Einführung
Thank you for Your Attention!
github.com/jgman86
jan.goettmann@uni-mainz.de
Lecture 3: Parameter Estimation I
By Jan Göttmann
