Seminar kognitive Modellierung:

Drift Diffusion Models

Jan Göttmann, M.Sc.

Datum Thema
25.10.2023 Organisation und Ablauf
08.11.2023 Einführung I + II : Grundlagen der Modellierung
15.11.2023 Parameterschätzung I: Diskrepanzfunktionen & Schätzalgorithmen
22.11.2023 Parameterschätzung II: Maximum Likelihood & Beyond
29.11.2023 Parameterschätzung III: Hands On in R Parameter Estimation
06.12.2023 Drift Diffusion Models (Theorie)
13.12.2023 Drift Diffusion Models (Anwendung)
20.12.2023 Advanced R (Asynchron)
10.01.2024 Multinomial Processing Tree Models  (Theorie)​
17.01.2024 Anwendung von MPT Modellen (R-Sitzung)​
24.01.2023 Mixture Models (Theorie)
31.01.2024 Mixture Models (Anwendung)
07.02.2024 Puffersitzung

Fahrplan

Einführung: Sequential

Sampling Models

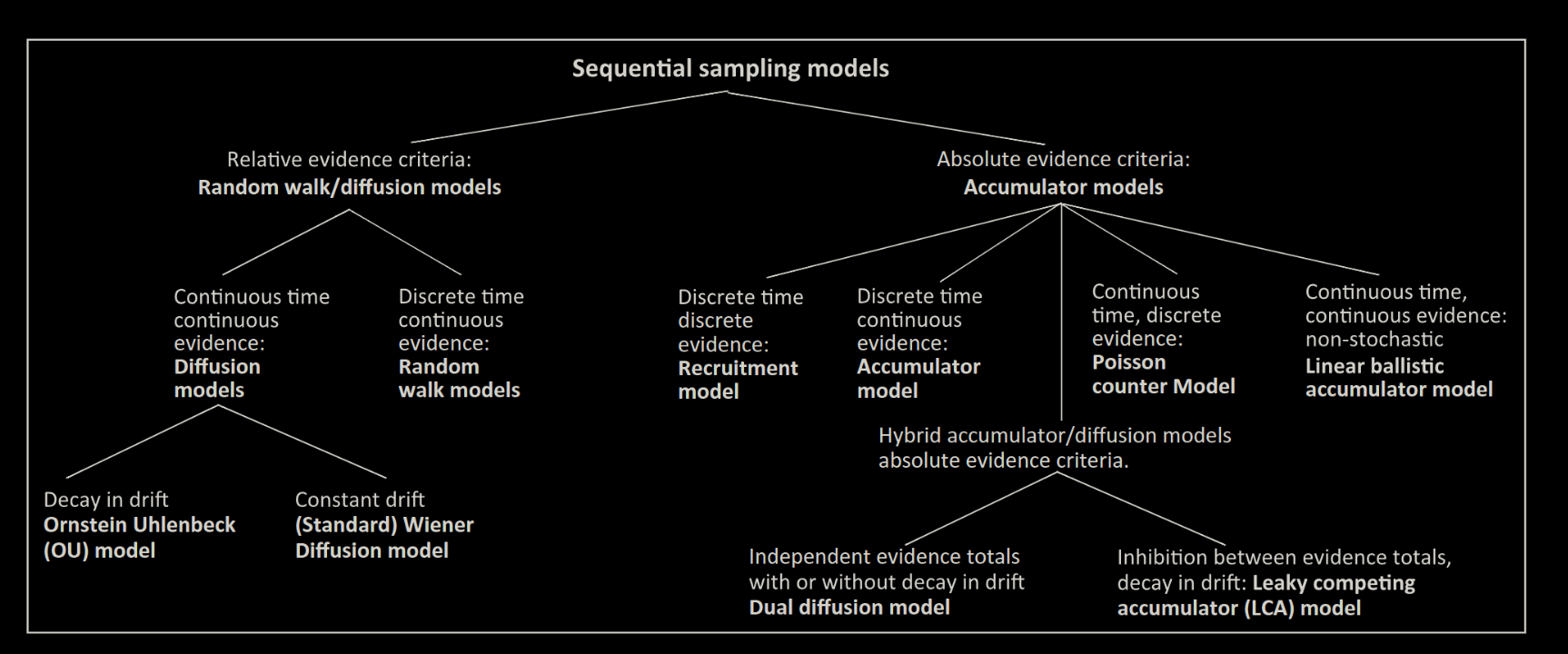
  • Erstmals 1978 publiziert (Ratcliff, 1978)
     
  • Anwendung aber schwierig, da Modell immer selbst auf den jeweiligen Anwendungsfall programmiert werden musste.
     
  • Ab 2007 / 2008 wurden verschiedene Tools veröffentlicht, die die Anwendungen stark vereinfachten:
    • EZ-diffusion Model (Grasman, Wagenmakers & van der Maas, 2009)
    • Diffusion Model Analysis Toolbox (DMAT; Vanderkerckhove & Tuerlinckx, 2007a, 2008)
    • fast-dm (Voss & Voss, 2008)

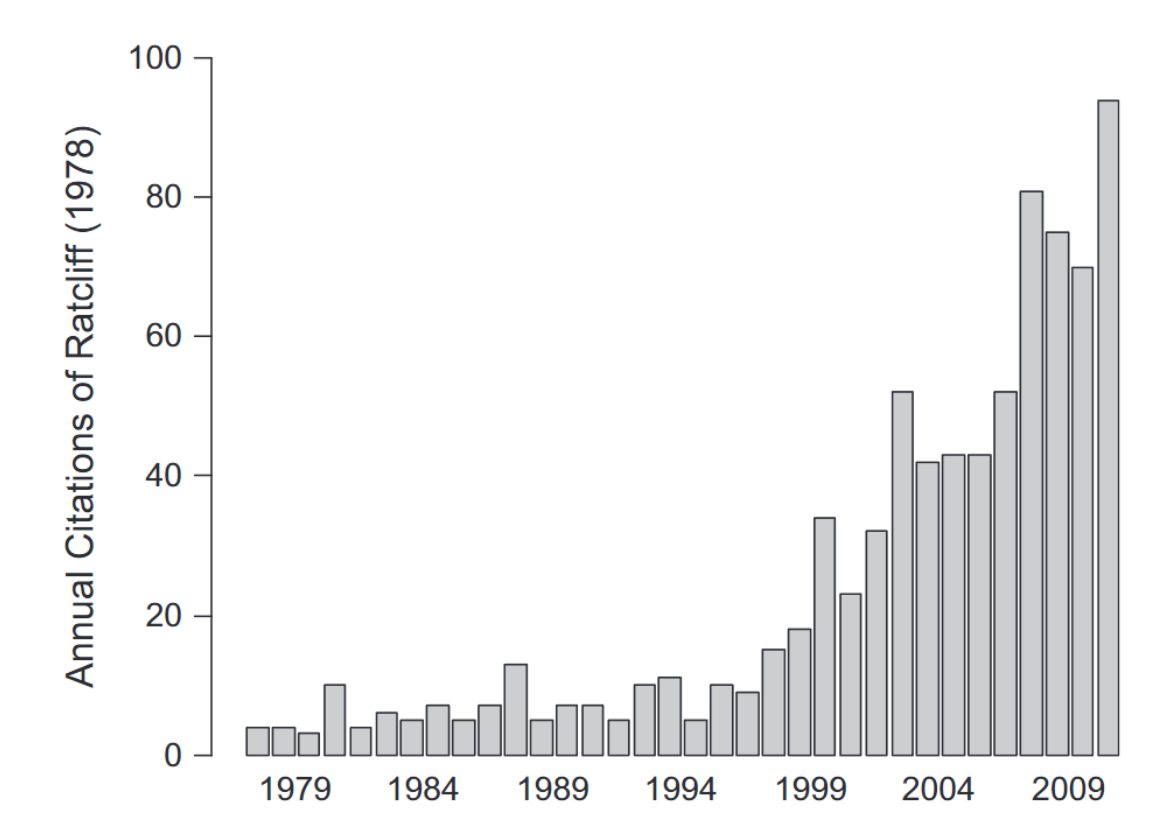
Das DDM ist ein sehr populäres Modell das in vielen Bereichen der Psychologie eingesetzt wird 

Anwendung in vielen Disziplinen der Psychologie

  • Implizte Einstellungen / Stereotype (Implicit Association Task)  (Klauer, Voss, Schmitz, & Teige Mocigemba, 2007)
  • First-Person-Shooter Task (Correll et al., 2015, Pleskac et al., 2017, Frenken et al., 2022)
  • Individual Differences in Intelligence 
    (Lerche et al., 2020, Schubert, Hagemann & Frischkorn,2017, 2016, van Ravenzwaaj, Brown & Wagenmakers, 2011)

Voss et al., 2013

Einführung: Sequential

Sampling Models

Einführung: Wiener Verteilung  

  • Positiver Bias

  • Right-Skewed

  • Modellierung durch Exponential-, Gamma-, Weibull, Lognormalverteilung oder Wiener Verteilung

Reaktionszeitverteilung

Wiener Verteilung (oder First Passage Time Distribution) als zu Grunde liegende Dichteverteilung des Diffusionsmodelles

\mu = 0.300 \\ \sigma^2 = 0.28
\text{Wiener}(rt|a, z, v) = \frac{a}{\sqrt{2\pi rt^3}} \exp \left( -\frac{(z-vrt)^2}{2rt} \right)

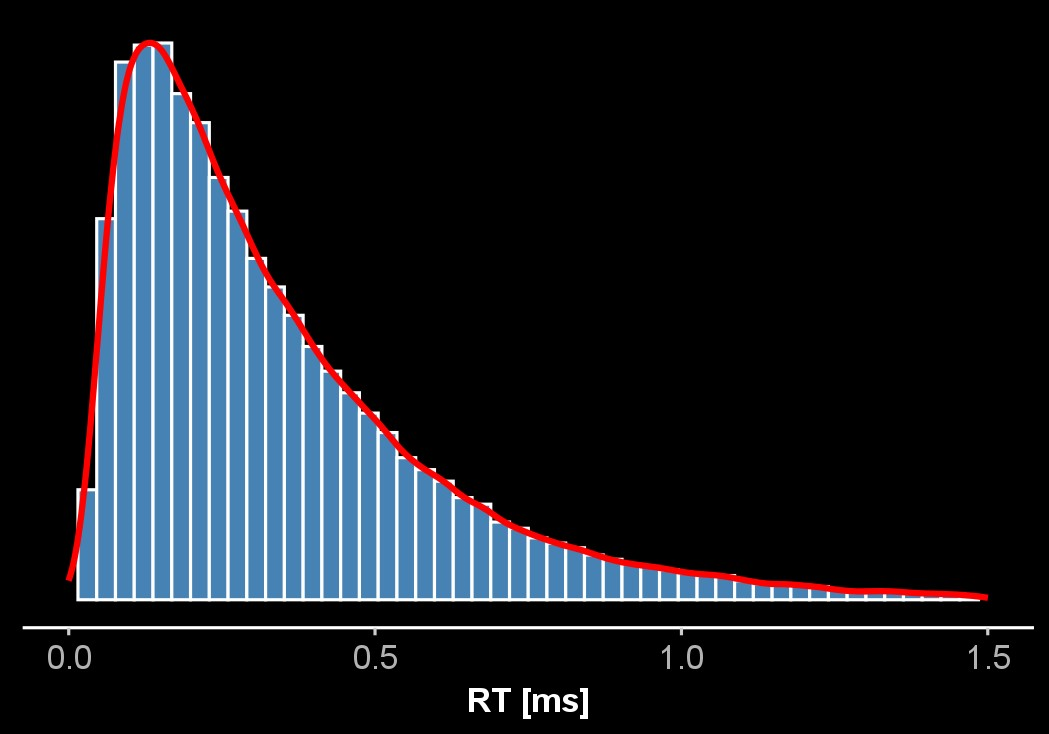
Wiener Verteilung Basismodell

Parameter der Wiener Verteilung bestimmen die Form der Reaktionszeitverteilung !

  • Modell zur Vorhersage von Reaktionszeitverteilungen und Entscheidungen in binären Entscheidungsaufgaben

  • Zerlegt den Reaktionsprozess vier unterschiedliche psychologische Parameter, nicht entscheidungsrelevante Prozesse \(t_0\) (Motorreaktion, Enkodierung etc.) werden als Konstante behandelt.

\text{RT} = rt + t_0

Einführung: Wiener Verteilung  

Grundannahmen DDM

\text{Wiener}(rt|a, z, v) = \frac{a}{\sqrt{2\pi rt^3}} \exp \left( -\frac{(z-vrt)^2}{2rt} \right)

  • Informationen für Entscheidung A oder B werden kontinuierlich über die Zeit t akkumuliert - kontinuierlicher Prozess
    ​

  • Die Veränderung der Informationsmenge für Entscheidung A oder B über die Zeit t wird als Diffusionsprozess bezeichnet ​
    ​

  • Dieser Prozess verläuft zwischen zwei Schwellen - für Entscheidung A oder B. Ist genug Information für entweder Entscheidung A oder B gesammelt, also die Schwelle erreicht, wird die Entscheidung getroffen.

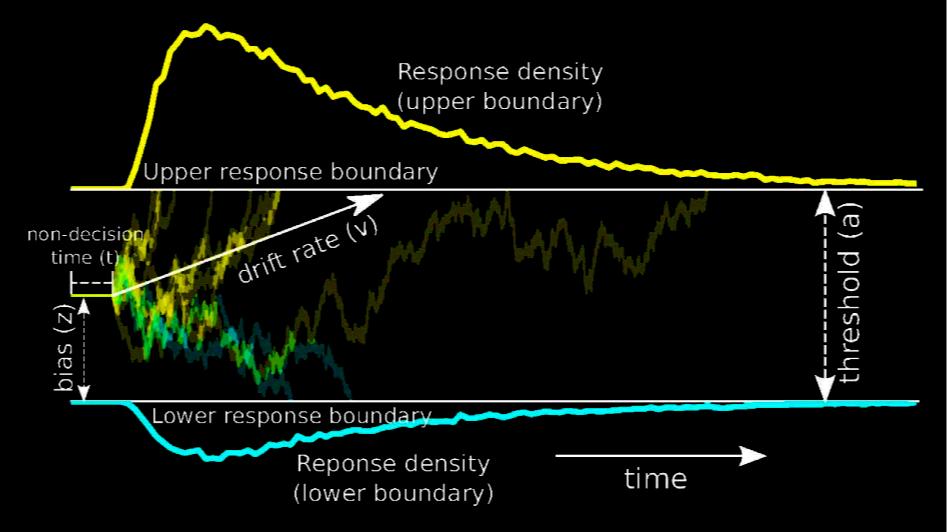
Einführung: Drift Diffusion Models  

Parameter des DDM

\text{Wiener}(rt|a, z, v) = \frac{a}{\sqrt{2\pi rt^3}} \exp \left( -\frac{(z-vrt)^2}{2rt} \right)

  1. Drift Rate (v): The speed and direction of evidence accumulation.

  2. Boundary Separation (a): The threshold of evidence needed to make a decision.

  3. Starting Point (z): Initial bias in evidence at the start of the decision process.

  4. Non-decision Time (t0): Time consumed by non-decision processes, like stimulus encoding and response execution.

Einführung: Drift Diffusion Models  

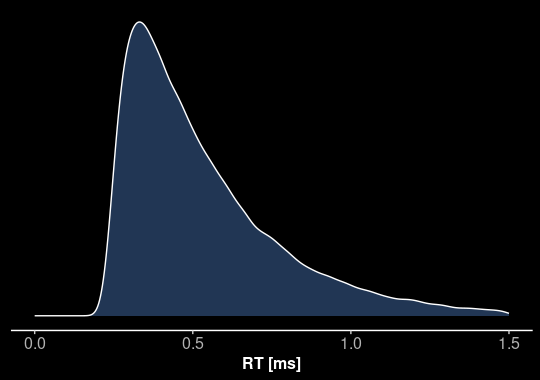
  • Jeder Parameter beeinflusst die vorhergesagten Reaktionszeitverteilungen – die gleiche Verteilung, kann durch unterschiedliche Prozesse erklärt werden!
     
  • Großer Vorteil bei der gezielten Manipulation von Prozessen im Experiment
\text{Wiener}(rt|a, z, v) = \frac{a}{\sqrt{2\pi rt^3}} \exp \left( -\frac{(z-vrt)^2}{2rt} \right)

Parameter des DDM

Beeinflusst die Verteilungen für korrekte und inkorrekte Antworten gleichermaßen!

v = 0.75 \\
a = 1.2 \\
z = 0.5 \\
t_0 = 0.2 \\

Einführung: Drift Diffusion Models  

\text{Wiener}(rt|a, z, v) = \frac{a}{\sqrt{2\pi rt^3}} \exp \left( -\frac{(z-vrt)^2}{2rt} \right)
v = 0.75 \\
a = 0.8 \\
z = 0.5 \\
t_0 = 0.2 \\
v = 2.00 \\
a = 0.8 \\
z = 0.5 \\
t_0 = 0.2 \\
v = 0.75 \\
a = 1.2 \\
z = 0.5 \\
t_0 = 0.4 \\
v = 0.75 \\
a = 1.2 \\
z = 0.8 \\
t_0 = 0.2 \\

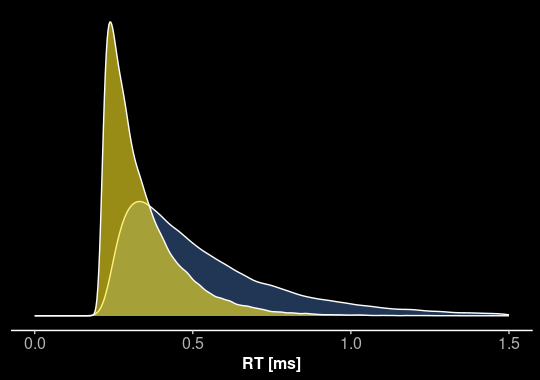
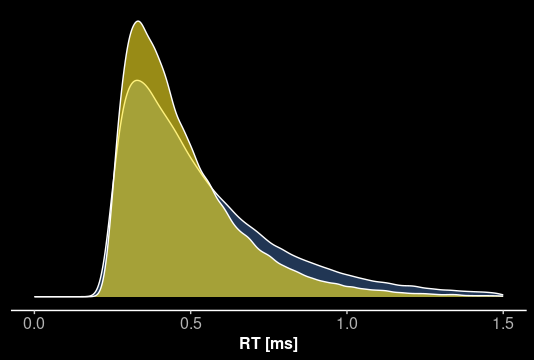
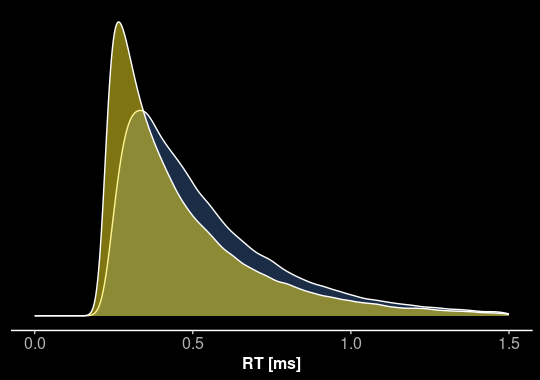
Einführung: Drift Diffusion Models  

Vorteile des DDM

  • Das DDM kann die gleichen Reaktionszeit- und Fehlerverteilungen durch unterschiedliche Kombinationen von Parametern erklären – Trennbar durch DDM!
  • Höhere statistische Power, da validere Maße für spezifische kognitive Prozesse (z.B. nicht-sign. Effekte auf Reaktionszeiten / Accuracies, aber auf die Driftrate ! )
  • Trennung sich überlagernder Prozesse – auffinden von Effekten die sonst nicht sichtbar sind: z.B. höhere Driftrate (v), aber motorisch langsamer(t0) und vorsichtiger (a)

Nachteile des DDM

  • Nur Anwendung für binäre Entscheidungsaufgaben (es existieren aber ähnliche Modelle für n-AFC Tasks)
  • Relativ hohe Anzahl von Trials notwendig für valide Schätzung
  • Parameterschätzung anfällig für „fast outliers“
  • Nur für schnelle Reaktionszeiten konzipiert ~ 1000 ms (neuere Studien belegen aber Validität auch für langsamere Reaktionszeiten)

 

Vorteile des DDM

Einführung: Drift Diffusion Models  

DDM: Anwendung

  • Evidenz für Zusammenhang zwischen allgemeiner Intelligenz und Driftrate; kein konsistenter Zusammenhang mit anderen DM-Parametern (z.B., McKoon & Ratcliff, 2012; Ratcliff, Thapar, & McKoon, 2011; Schmiedek, Oberauer, Wilhelm, Süß, & Wittmann, 2007)
  • Latente Korrelationen zwischen Drift-Rate-Faktor und allgemeiner Intelligenz r = .45, bei langsamen Aufgaben
    r =.68 (Lerche et al.,2020)
  • Auch Zusammenhänge von Domänenspezifische Driftfaktoren, die mit jeweiliger Intelligenztestskala zusammenhängen r = .50 – r = .90 (Lerche et al.,2020)

 

Intelligenz

 

Typischer Befund: Ältere Teilnehmer haben längere Reaktionszeiten, kein Unterschied in Fehlerraten

  • Klares Ergebnismuster:
    • Schwellenabstand: höher bei Älteren (z.B. Ratcliff, Thapar, & McKoon, 2001; Schuch, 2016)
    • Non-decision time: höher bei Älteren (z.B. Ratcliff, Thapar,& McKoon, 2001; Ratcliff, Thapar, & McKoon, 2004)
    • Driftrate
      • Gedächtnisaufgaben und perzeptuelle Aufgaben: Jüngere sind Älteren überlegen
      • Lexikalische Aufgaben: Ältere sind Jüngeren überlegen
      • Perzeptuelle und lexikalische Aufgaben: Ältere profitieren von erhöhter Aufgabenschwierigkeit (Theisen, Lerche, v. Krause, & Voss, 2020)

 

 

Altern

ADHS-Patienten vs. gesunder Kontrollgruppe: Vergleich der DM-Parameter​

  • konsistent: kein Effekt im Schwellenabstand​
  • konsistent: Driftrate geringer als bei KG ​(Karalunas & Huang-Pollock, 2013; Metin, Roeyers, Wiersema, van der Meere, Thompson, & Sonuga- Barke, 2013; Weigard & Huang-Pollock, 2014).​

  • Häufig geringere non-decision time als Kontrollgruppe (aber Karalunas, Huang-Pollock, & Nigg, 2012).​

Klinische Psychologie

DDM: Anwendung

Shooter Bias (Payne, 2001; Unkelbach et al., 2008)​

  • Typische Befunde: Schnellere Reaktionszeiten bei Stereotype-Consistent Stimuli & geringere Fehlerraten
  • Aber welche Prozesse sind beteiligt ? Lösung DDM Modellierung !

 

 

 

  • Stereotype (z.B. Bedrohlichkeit) können erlernt werden und zeigen sich als verschobener Bias im DDM (Startpunkt)
  • Replikation bisheriger Befunde: Schnellere Reaktionszeiten in Stererotyp-Cosistent Trials (z.B. Schwarz  +  Waffe schneller als Schwarz + Werkzeug)
  • Aber: Schneller Reaktionszeiten werden durch unterschiede in der non-decision time vermittelt, nicht durch die Driftrate oder einen a priori bias ! 

Frenken et al., 2022

DDM: Anwendung

Shooter Bias (Payne, 2001; Unkelbach et al., 2008)​

  • Typische Befunde: Schnellere Reaktionszeiten bei Stereotype-Consistent Stimuli & geringere Fehlerraten
  • Aber welche Prozesse sind beteiligt ? Lösung DDM Modellierung !

 

 

 

  • Stereotype (z.B. Bedrohlichkeit) können erlernt werden und zeigen sich als verschobener Bias im DDM (Startpunkt)
  • Replikation bisheriger Befunde: Schnellere Reaktionszeiten in Stererotyp-Cosistent Trials (z.B. Schwarz  +  Waffe schneller als Schwarz + Werkzeug)
  • Aber: Schneller Reaktionszeiten werden durch unterschiede in der non-decision time vermittelt, nicht durch die Driftrate oder einen a priori bias ! 

Frenken et al., 2022

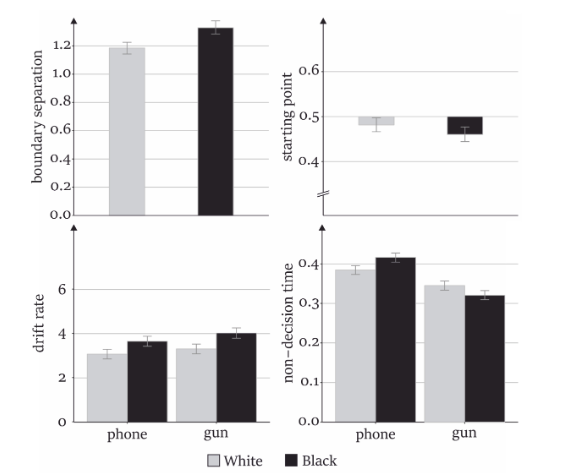
Frenken et al., 2022

DDM: Anwendung

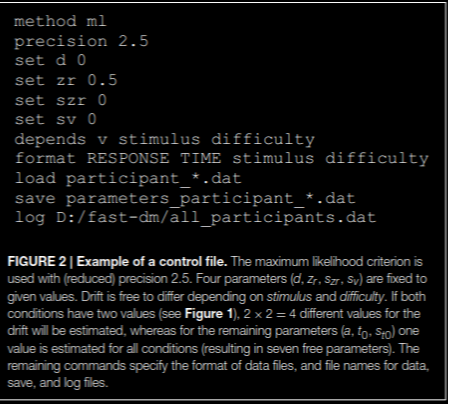
Schätzprogramme

  1. fast-dm30.2 (Voss & Voss, 2003)
  • Schätzung mit verschiedenen Diskrepanzfunktionen
    • Maximum Likelihood
    • Kolmogorov-Smirnoff
    • Chi-Square
  • Schätzunge von erweiterten Modellen möglich (variabilität von Parametern)
  • Sehr flexibel und anpassbar auf experimentelle Bedingungen.

Pro

Contra

  • Bediehnung für Laien schwierig
  • nur command line Interface
  • Keine systematischen Recovery Studien

DDM: Anwendung

Schätzprogramme

2. EZDiffusion Model (Wagenmakers, van Der Maas, Grasman,2007)

  • Vereinfachun des Diffusionsmodelles, Parameter sind "berechenbar" durch drei einfache Gleichungen
  • Sehr wenig Daten notwendig
  • Einfach Anwendung in R ohne zusätzliche Software

Pro

Contra

  • Nur Approximierung der Parameter
  • Keine Schätzung von erweiterten DDMs möglich (Parametervariabilität)
  • Keine systematischen Recovery Studien

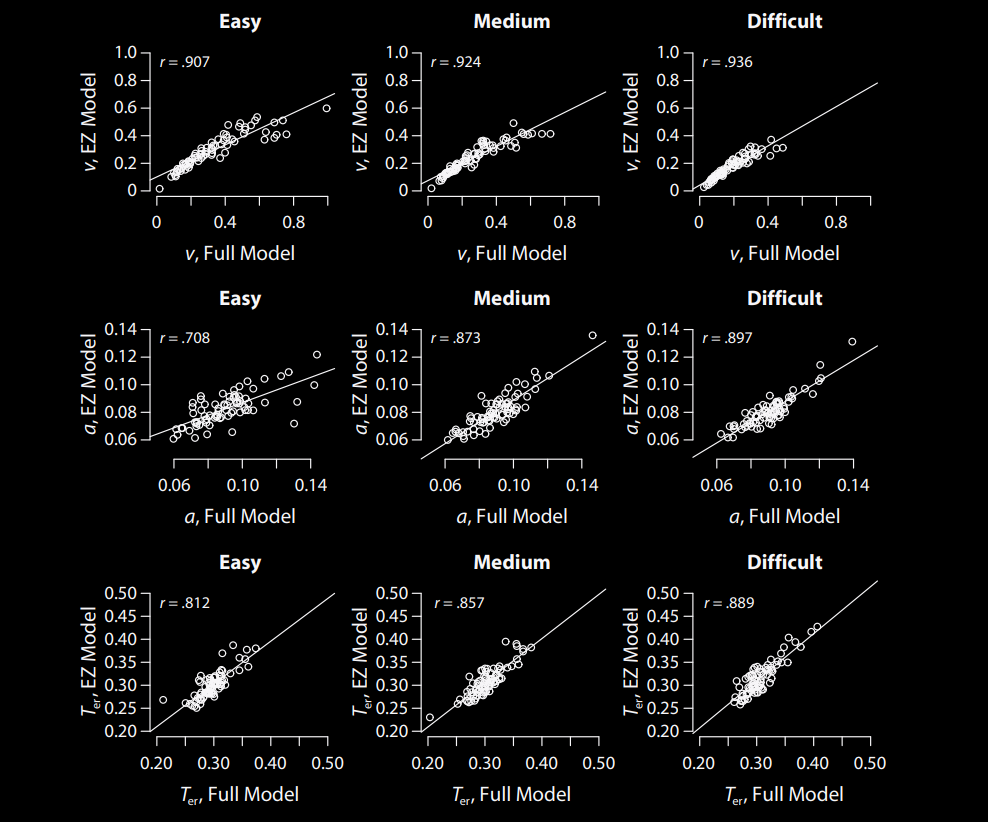
Wagenmakers et al.,2007)

DDM: Anwendung

Thank you for Your Attention!

github.com/jgman86

jan.goettmann@uni-mainz.de

AMD-Lab@Uni-Mainz

Lecture 8: Drift Diffusion Models

By Jan Göttmann

Made with Slides.com

Lecture 8: Drift Diffusion Models

  • 167

More from Jan Göttmann