Deep Generative models (VAEs) for ODEs with knows and unknowns
Harshavardhan Kamarthi
Data Seminar
Variational Auto-Encoder
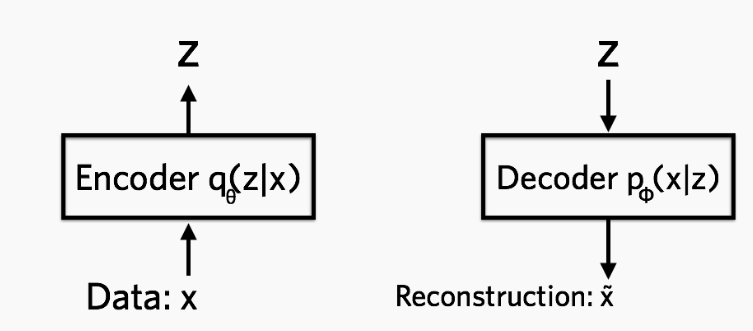
- Goal: Learn distribution p(X)
- Encode x towards a known distribution on latent variable z. Decode z to x
Variational Auto-Encoder
Encoder
Prior on latent variable . Usually set as standard Gaussian.
Decoder
Variational ELBO Loss
q(z∣x)
q(z|x)
p(z)
p(z)
p(x∣z)
p(x|z)
−Eq(z∣x)[logp(x∣z)]+KL[q(z∣x)∣∣p(z)]
-E_{q(z|x)}[\log p(x|z)] + KL[q(z|x)||p(z)]
Physics based VAEs
- Model data from complex ODEs
- Learn low-dimensional latent representations from data
- Learn relation between observed state and latent state where latent states are governed by ODE
- Learn parameters of the latent ODE
ODE2VAE: Deep generative second order ODEs with Bayesian neural networks
z1
z_1
z2
z_2
z3
z_3
…
\dots
…
\dots
zN
z_N
x1
x_1
x2
x_2
x3
x_3
…
\dots
…
\dots
xN
x_N
Yidiz et al (NIPS '19)
ODE2VAE: Deep generative second order ODEs with Bayesian neural networks
No information about the functional form
Goals:
- Learn low lank representations from sequential data
- Extrapolate/forecast
Z
Z
{xN+1,xN+2,…}
\{x_{N+1}, x_{N+2}, \dots\}
Second-order Bayesian ODE
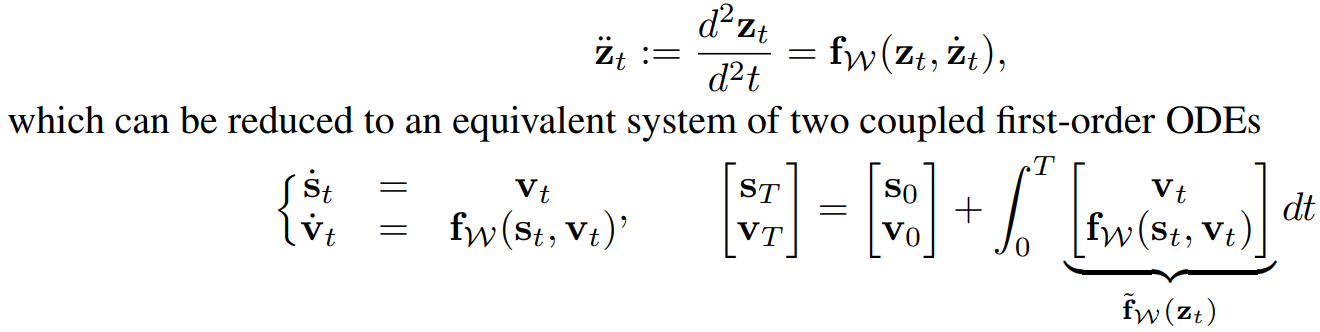
- Second-order: to model higher-order dynamics
- is a Bayesian Neural network with prior
- To capture uncertainty
fW
f_{\mathcal{W}}
p(W)
p(\mathcal{W})
ODE2VAE Model
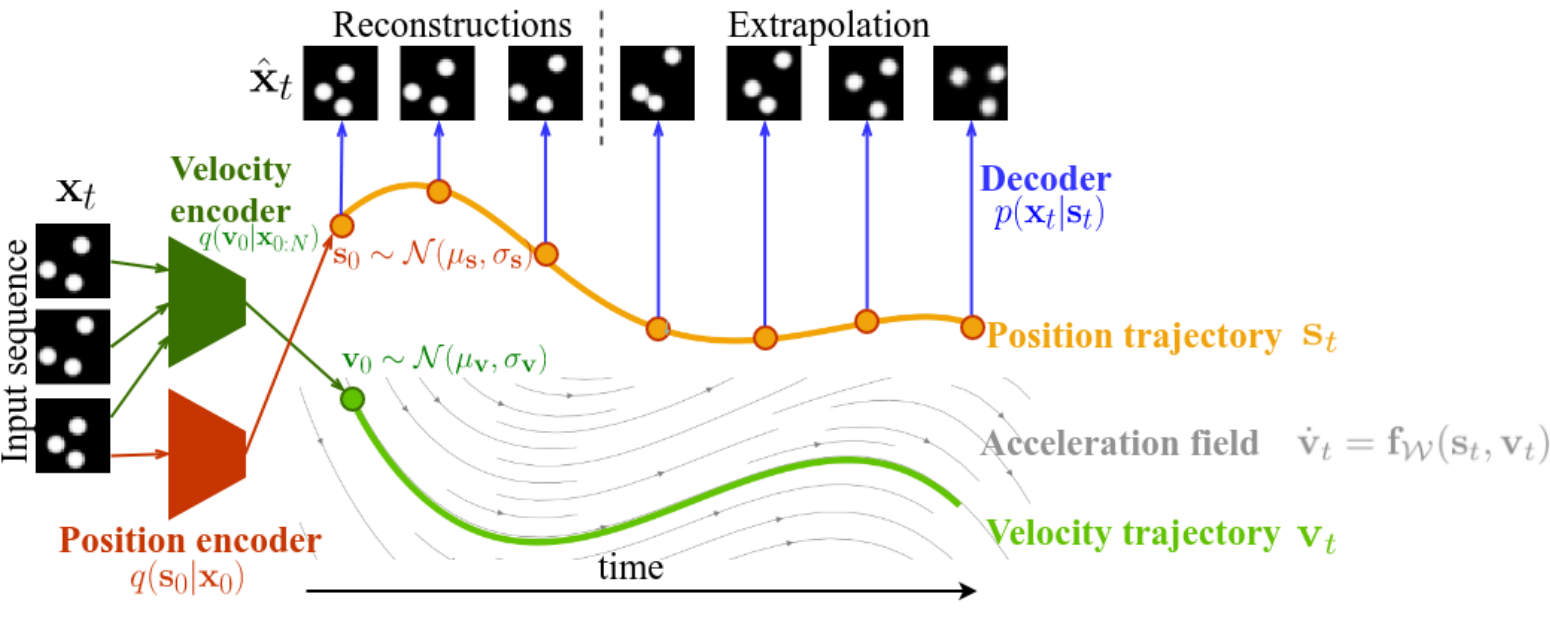
ODE2VAE Encoder
q(W,Z∣X)=q(W)qenc(z0∣X)qode(Z[1:N]∣X,z0,W)qenc(z0∣X)=N((μs(x0),μv(X[0:M])),diag(σs(x0),σv(X[0:M])))logq(zT∣W)=logq(z0∣W)−∫0TTr(∂vt∂fW(st,vt))
q(\mathcal{W}, Z|X) = q(\mathcal{W})q_{enc}(z_0|X)q_{ode}(Z[1:N]|X,z_0,\mathcal{W})\\
q_{enc}(z_0|X) = \mathcal{N}((\mu_s(x_0), \mu_{v}(X[0:M])), diag(\sigma_s(x_0), \sigma_v(X[0:M])))\\
\log q(z_T|\mathcal{W}) = \log q(z_0|\mathcal{W}) - \int_{0}^{T} Tr\left( \frac{\partial f_{\mathcal{W}(s_t, v_t)}}{\partial v_t} \right)
Note:
- Transition function is stochastic
- 3rd equation derived by "Change of variable" theorem (approximated by Runge-Kutta method)
ODE2VAE Decoder
p(xt∣zt)
p(x_t|z_t)
is deterministic NN decoder
ODE2VAE Learning
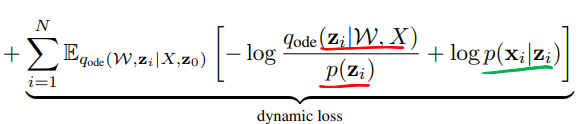
ODE2VAE Learning
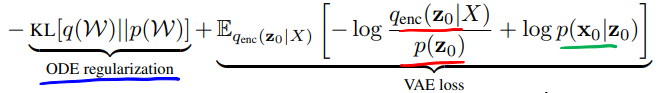
- Dynamic loss dominates VAE loss due to long trajectories
- Data may underfit to encoder distribution
- Add regularizer to make ode and encoder distribution similar
−γEq(W)[KL[qode(Z∣X)∣∣qenc(Z∣W,Z)]]
-\gamma E_{q(\mathcal{W})}[KL[q_{ode}(Z|X) || q_{enc}(Z|\mathcal{W},Z)]]
Extrapolation Results
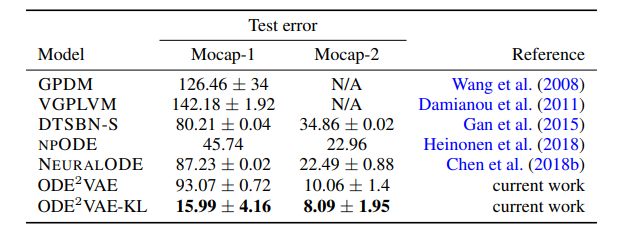
CMU-Walking data (Extrapolate last 1/3 rd trajectory)
Rotating MNIST
Bouncing Ball
Generative ODE Modelling with Known and Unknowns
z1
z_1
z2
z_2
z3
z_3
…
\dots
…
\dots
zN
z_N
x1
x_1
x2
x_2
x3
x_3
…
\dots
…
\dots
xN
x_N
(ω1,ω˙1)
(\omega_1, \dot{\omega}_1)
(ω2,ω˙2)
(\omega_2, \dot{\omega}_2)
(ω3,ω˙3)
(\omega_3, \dot{\omega}_3)
(ωN,ω˙N)
(\omega_N, \dot{\omega}_N)
Linial et al (CHIL '21)
Generative ODE Modelling with Known and Unknowns
Given the functional form:
dtdzi=fθ(zi)
\frac{dz_i}{dt} = f_{\theta}(z_i)
Estimate
1. Parameters
2. Extrapolate
θ
\theta
{xN+1,xN+2,…}
\{x_{N+1}, x_{N+2}, \dots\}
Encoder
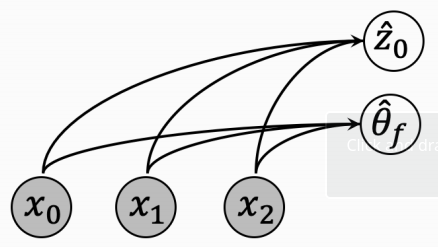
Use RNNs to encode latent variables and then transform to "physics grounded form"
[μz~0,σz~0]=RNNz~0(X)q(z0~∣X)=N(μz~0,σz~0)p(z0~)=N(0,I)z0=hz(z0~)
[\mu_{\tilde{z}_0}, \sigma_{\tilde{z}_0}] = RNN_{\tilde{z}_0}(X)\\
q(\tilde{z_0}|X) = \mathcal{N}(\mu_{\tilde{z}_0}, \sigma_{\tilde{z}_0})\\
p(\tilde{z_0}) = \mathcal{N}(0,I)\\
z_0 = h_z(\tilde{z_0})
[μθ~0,σθ~0]=RNNθ~0(X)q(θ0~∣X)=N(μθ~0,σθ~0)p(θ0~)=N(0,I)θ0=hθ(θ0~)
[\mu_{\tilde{\theta}_0}, \sigma_{\tilde{\theta}_0}] = RNN_{\tilde{\theta}_0}(X)\\
q(\tilde{\theta_0}|X) = \mathcal{N}(\mu_{\tilde{\theta}_0}, \sigma_{\tilde{\theta}_0})\\
p(\tilde{\theta_0}) = \mathcal{N}(0,I)\\
\theta_0 = h_\theta(\tilde{\theta_0})
Decoder
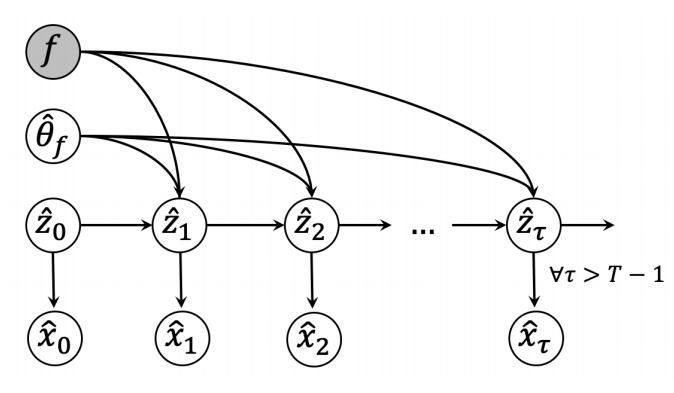
Transition probabilities on latent space is deterministic:
defined from
Transformation to observation space is deterministic via neural network:
defined from
q(zt∣zt−1,θ)
q(z_t|z_{t-1}, \theta)
dtdzi=fθ(zi)
\frac{dz_i}{dt} = f_{\theta}(z_i)
xi=gϕ(zi)
x_i = g_{\phi}(z_i)
p(xi∣zi)
p(x_i|z_i)
Learning
Generative Distribution
p(X,Z,θ,z~0,θ~0)=p(z~0)p(θ~0)p(z0∣z~0)p(θ0∣θ~0)p(x0∣z0)∏i=1Np(zi∣zi−1,θ)p(xt∣zt)
p(X,Z,\theta, \tilde{z}_0, \tilde{\theta}_0) = p(\tilde{z}_0) p(\tilde{\theta}_0) p(z_0|\tilde{z}_0) p(\theta_0|\tilde{\theta}_0)
p(x_0|z_0)\prod{i=1}^{N}p(z_i|z_{i-1}, \theta) p(x_t|z_t)
Minimize ELBO
Eq(Z,θ,θ~,z~0)∣X[logp(X∣Z,θ,θ~,z~0)]−KL[q(Z,θ,θ~,z~0)∣X)∣∣p(Z,θ,θ~,z~0)]
E_{q(Z,\theta, \tilde{\theta}, \tilde{z}_0)|X}[\log p(X|Z,\theta, \tilde{\theta}, \tilde{z}_0)] -
KL[q(Z,\theta, \tilde{\theta}, \tilde{z}_0)|X)|| p(Z,\theta, \tilde{\theta}, \tilde{z}_0)]
=(∑n=0NEq(zt∣X)[logp(xt∣zt)])−KL[q(θ~∣X)∣p(θ~)]−KL[q(z~0∣X)∣p(z~0)]
=\left( \sum_{n=0}^N E_{q(z_t|X)}[\log p(x_t|z_t)]\right)
- KL[q(\tilde{\theta}|X) | p(\tilde{\theta})]
- KL[q(\tilde{z}_0|X) | p(\tilde{z}_0)]
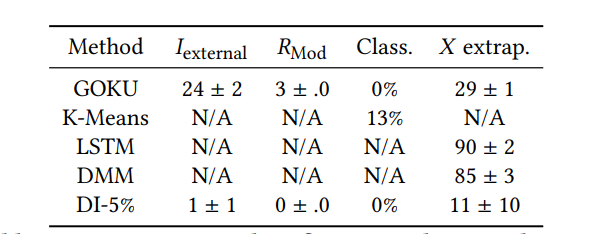
Results
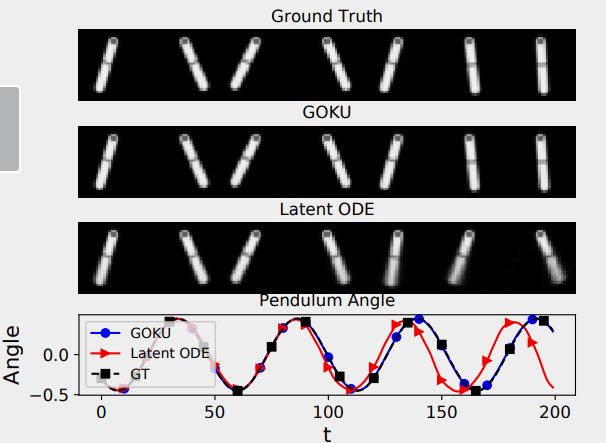
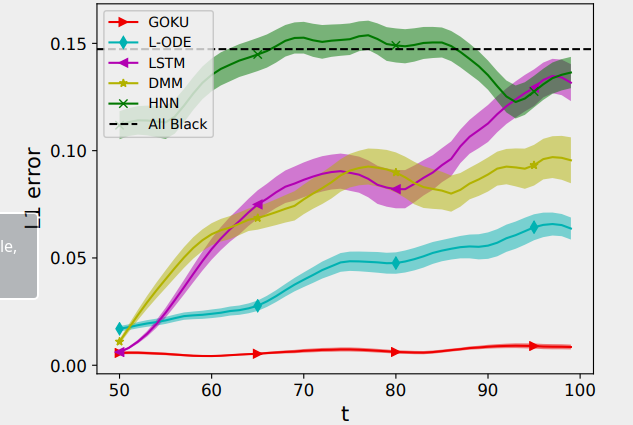
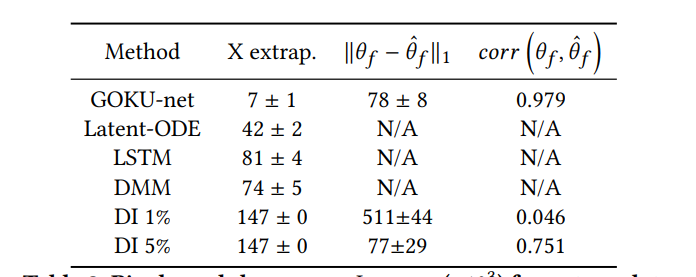
Similarly outperformed baselines significantly for double pendulum a CVS model
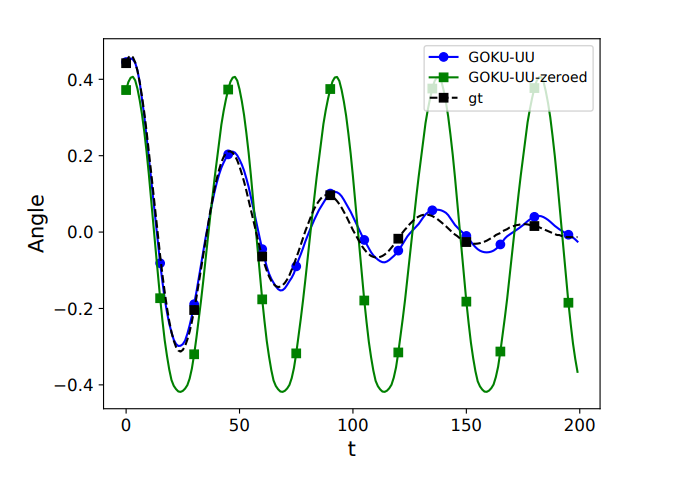
What if part of functional is unknown?
ω˙(t)=−lgsin(θ)−mbω(t)
\dot{\omega}(t) = -\frac{g}{l}sin(\theta) - \frac{b}{m}\omega(t)
Unknown
Then add NN to learn the unknown:
dtdzt=fθ(zt)+fabs(zt,θ)
\frac{dz_t}{dt} = f_{\theta}(z_t) + f_{abs}(z_t, \theta)
What if part of functional is unknown?
Physics-Integrated Variational Autoencoders for Robust and Interpretable Generative Modeling
- Functional is partially known
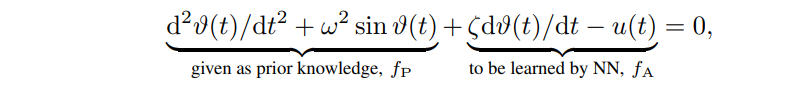
- known part of functional
- Model and extrapolate
fP(v,ω)=v¨+ω2sin(v)
f_P(v, \omega) = \ddot{v} + \omega^2 \sin (v)
{v(0),v(Δt),…,v(τΔt)}
\{v(0), v(\Delta t), \dots, v(\tau \Delta t)\}
Takeishi et al '21
Encoder
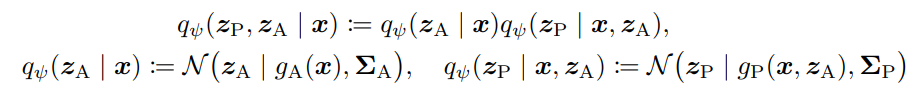
- are neural networks, are also trainable parameters
gA,gP
g_A, g_P
ΣA,ΣP
\Sigma_A, \Sigma_P
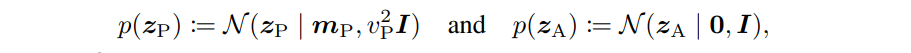
- are defined using domain information
mP,vP2
\mathbf{m}_P, v_P^2
Divide latent encoding into known and unknown parts
Decoder
pθ(x∣zP,zA)=N(fA(fP(zP),zA),ΣX)
p_{\theta}(x|z_P, z_A) = \mathcal{N}(f_A(f_P(z_P), z_A), \Sigma_X)
- is neural network
- is from solution of ODE on
fA
f_A
fP
f_P
zP
z_P
Focusing on Physics-based component
- can dominate training ignoring
- Define a Physics-only reduced model
- Where , the baseline function is another NN with trainable parameter
- Then add regularizer
fA
f_A
fP
f_P
hA
h_A
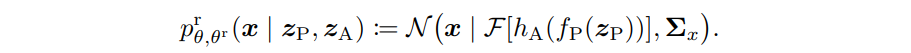
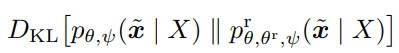
Physics-based data augmetation
- Goal: ground outputs of which are parameters of
- Idea: Use physics model as data augmentation to train
- Sample from
- Generate
- Train to estimate from
gP
g_P
fP
f_P
fP
f_P
gP
g_P
zP
z_P
p(zP)
p(z_P)
xP=hA(fP(zP))
x_P = h_A(f_P(z_P))
gP
g_P
xP
x_P
zP
z_P
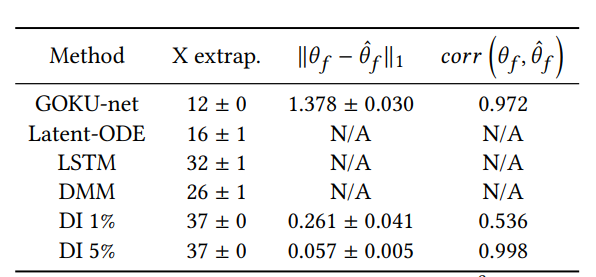
Results
Deep Generative models (VAEs) for ODEs with knows and unknowns Harshavardhan Kamarthi Data Seminar
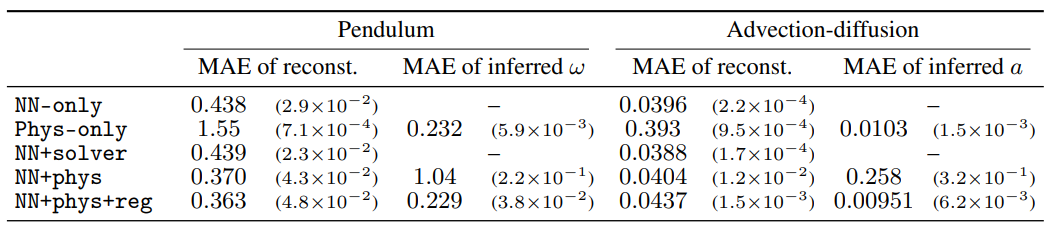
Physice ODE
By Harshavardhan Kamarthi
Physice ODE
- 135
