COMP2521
Data Structures & Algorithms
Week 8.3
Merge Sort
Author: Hayden Smith 2021
In this lecture
Why?
- We need some algorithms better than O(n^2) for large data sets.
What?
- Merge sort
Mergesort Overview
The key of this approach is that it's recursive.
- Split the array into two roughly equal sized partitions
- Recursively sort each of the partitions
- Merge the two partitions into a new sorted array
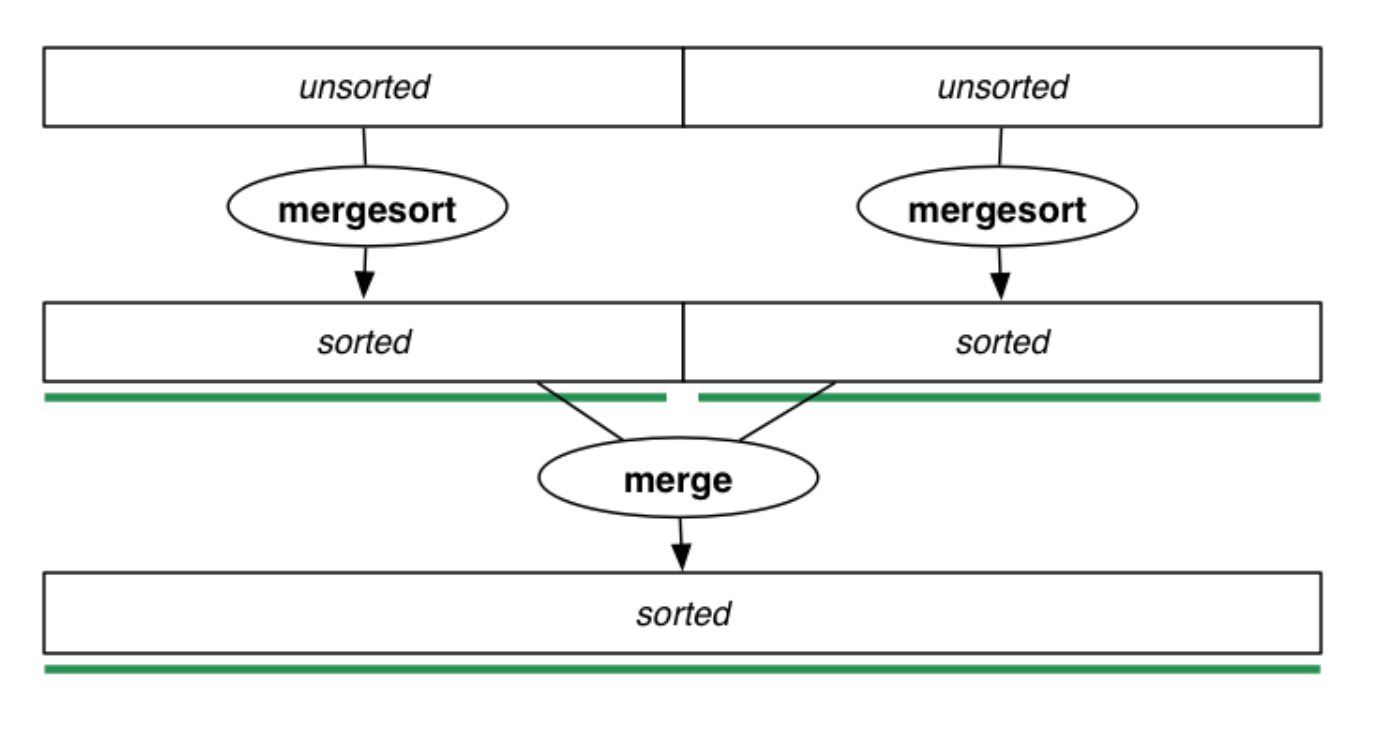
Mergesort Overview
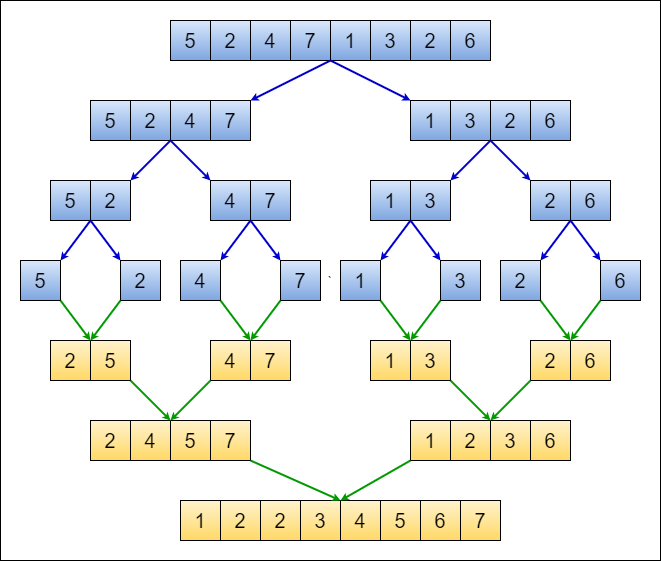
Source: https://levelup.gitconnected.com/visualizing-designing-and-analyzing-the-merge-sort-algorithm-cf17e3f0371f
Split / Divide
Merge
Implementation
void mergesort(Item a[], int lo, int hi)
{
int mid = (lo + hi) / 2; // mid point
if (hi <= lo) return;
mergesort(a, lo, mid);
mergesort(a, mid+1, hi);
merge(a, lo, mid, hi);
}
int main() {
int nums[10] = {32,45,17,22,94,78,64,25,55,42};
mergesort(nums, 0, 9);
}Merge sort is kind of like a binary tree split where the re-merging happens post-fix.
The function "merge" has to merge two sorted arrays back together.
Implementation
void merge(Item a[], int lo, int mid, int hi) {
int i, j, k, nitems = hi - lo + 1;
Item *tmp = malloc(nitems * sizeof(Item));
i = lo; j = mid + 1; k = 0;
// scan both segments, copying to tmp
while (i <= mid && j <= hi) {
if (leq(a[i], a[j]))
tmp[k++] = a[i++];
else
tmp[k++] = a[j++];
}
// copy items from unfinished segment
while (i <= mid) tmp[k++] = a[i++];
while (j <= hi) tmp[k++] = a[j++];
//copy tmp back to main array
for (i = lo, k = 0; i <= hi; i++, k++)
a[i] = tmp[k];
free(tmp);
}The merge function
Performance

Split / Divide
We have to split our list log(N) times
Merge
We have to merge N numbers exactly log(N) times
This part requires extra memory :(
O(log(N))
O(N * log(N))
Performance
Mergesort has both a best and worst case of O(N*log(N))
Whether the list is fully sorted, or fully reverse sorted, the same steps are taken
This makes it time-wise generally better than quicksort - however - we need extra memory for this.
Linked Lists
Whilst mergesort typically operates on arrays, it's also possible to do it on linkedlists. We won't go into any detail on this.
Feedback

COMP2521 21T2 - 8.3 - Merge Sort
By haydensmith
COMP2521 21T2 - 8.3 - Merge Sort
- 1,440



