數論
楊皓丞
數論
- 數學中最理論的領域
- 卻能應用於非常實務的層面
- 是迎戰資奧必備的知識
- 也是資訊科學中重要的工具
- 被稱為“數學中的皇后”
Let's start from 1,2,3!
為什麼人類需要數字?
因為我們需要“個數”的概念
最初的數字系統對應到現在的哪種數字?
既然是“個數”,當然是正整數!
1隻羊,2隻羊,3隻羊
1天,2天,3天
這就是最以前唯一需要數字之處!
現在數學家如何定義正整數呢?
定義1為正整數,定義2為正整數,...?
不可能,永遠定義不完
定義0~9的任意個數,無前置0的排列
為正整數?
正整數的定義:
1. 1是正整數
2. 任一個正整數的“下一個數字”也是正整數
聽起來很唬爛吧?
正整數的正式定義:
1. \( 1 \in \mathbb{N} \)
2. \( x \in \mathbb{N} \Rightarrow s(x) \in \mathbb{N} \)
所以,\(1, s(1), s(s(1)), ... \) 都是正整數
為了方便書寫,
我們把s(1)記做2,s(s(1))記做3...
現在有正整數的定義了,對於正整數,最重要的莫過於加法了
(記得嗎,正整數是為了表示個數,而個數最重要的就是要能加起來)
如何定義加法呢?
加法的定義:
1. \( 1 + x = s(x) \)
2. \( s(x)+ y = x + s(y) \)
\( s(s(1))+ s(s(1)) = s(1) + s(s(s(1))) \)
\( = 1 + s(s(s(s(1)))) = s(s(s(s(s(1))))) \)
也就是3+3=6
有加法了!
現在我知道鄰居送我兩隻羊後我會有幾隻羊了。接著呢?
家裡每個小孩要吃兩碗飯,媽媽晚上要煮幾碗飯的份量?
乘法的定義:
1. \( 1 \times x = x \)
2. \( s(x) \times y = y + x \times y \)
太棒了!有了加法和乘法幾乎就已經征服正整數了,次方運算也是正整數重要的運算,大家可以自己試著定義看看
整個整數域就是正整數再加上0和負整數而已,也不難定義
整數的定義:
1. \( 0 \in \mathbb{Z} \)
2. \( x \in \mathbb{Z} \Rightarrow s(x) \in \mathbb{Z} \)
3. \( s(x) \in \mathbb{Z} \Rightarrow -s(x) \in \mathbb{Z} \)
整數的加法和乘法的定義也很類似,大家自己試試看!
當然,我很想繼續跟大家討論為何後來接著出現有理數,實數,複數,但整數的數論和應用就已經夠我們討論一整天了!
今天只會用到整數,其實很簡單吧XD
質數與合數
質數與合數
- 小學就學過了,快速複習一下!
- 正整數可以分為1,質數,合數
- 合數可以被表示成兩個不是1的正整數的乘積
- 質數不行
- 1就是1
- 質數和合數都有無限多個!(why?)
質數篩法
- 問題:如何找到1到N中所有質數
- 法1:\(O(N^2)\)看看每個數有沒有不是1和自己的因數
int not_prime[N]={0};
vector<int> prime;
void prime_sieve(){
not_prime[1]=1;
for(int i=2;i<N;i++){
for(int j=2;j<i;j++)
if(i%j==0)
not_prime[i]=1
if(!not_prime[i])
prime.push_back(i);
}
}比較好的質數篩法
- 法2:每個質數的兩倍以上的倍數都不是質數,劃掉!
- 一個數字最多只會被劃掉\(lgN\)次,複雜度\(O(NlgN)\)
- \(N<10^7\)時,一個數字最多只會被劃掉8次!
int not_prime[N]={0};
vector<int> prime;
void prime_sieve(){
not_prime[1]=1;
for(int i=2;i<N;i++){
if(!not_prime[i]){
prime.push_back(i);
for(int j=2;i*j<N;j++)
not_prime[i*j]=1;
}
}
}最好的質數篩法
- 法3:讓每個合數只會被自己最小的質因數劃掉!
- 一個數字只會被劃掉1次,複雜度\(O(N)\)
- 稱為線性篩法,是最廣為使用的
int not_prime[N]={0};
vector<int> prime;
void prime_sieve(){
not_prime[1]=1;
for(int i=2;i<N;i++){
if(!not_prime[i]){
prime.push_back(i);
}
for(int j=0;j<prime.size()&&i*prime[j]<N;j++){
not_prime[i*prime[j]]=1;
if(i%prime[j]==0)
break;
}
}
}最大公因數
- 給定兩數\(p,q\),如何求最大公因數相信大家都很熟悉了
- 輾轉相除法!但是為什麼?
int gcd(int p,int q){
if(q==0)return p;
return gcd(q,p%q);
}
最大公因數
- 根據餘數定理,對於任何除數和被除數,可以唯一寫成
\(n=qm+r\) ,其中\(n,m,q,r\)分別為被除數,除數,商,餘數
並滿足\(0 \leq r \lt m \) - \(n\)和\(m\)的最大公因數,就是\(m\)和\(r\)的最大公因數!
- 時間複雜度:\(O(log(n+m))\),為什麼?
裴蜀定理
a,b為給定兩數,
\(ax+by=1\)有整數解\( \Leftrightarrow gcd(a,b)=1\)
此定理可以推廣成
\(ax+by=m\)有整數解\( \Leftrightarrow gcd(a,b)|m\)
裴蜀定理
找整數解的方式,跟\(gcd\)差不多,用輾轉相除法!
int extgcd(int p,int q,int &x,int &y){
if(q==0){
x=1,y=0;
return p;
}
int ret=extgcd(q,p%q,y,x);
y-=(p/q)*x;
return ret;
}
算術基本定理
- 若\(n>1\),存在唯一的方式將\(n\)分解成質數乘積
\[n= p_1^{n_1}p_2^{n_2} \cdots p_k^{n_k}\] - 為什麼一定存在一種方法?
- 為什麼一定只有一種方法?
- 白話的說,正整數的質因數分解是唯一的
質因數分解
- 法1:建完質數表後每個質數都拿去除除看能除幾次,最大的質因數有可能大到是自己的一半,所以每次分解複雜度\(O(N)\)
void prime_sieve(){
//...
}
vector<PII> factorization(int N){
vector<PII> factors;
for(int i=0;i<prime.size()&&prime[i]<=N;i++){
int cnt=0;
while(N%prime[i]==0){
cnt++;
N/=prime[i];
}
if(cnt)
factors.push_back(make_pair(prime[i],cnt));
}
return factors;
}
質因數分解
- 法2:建完質數表後每個質數都拿去除除看能除幾次,每個數只會有一個大於自己開根號的質因數!\(O(\sqrt{N})\)
void prime_sieve(){
//...
}
vector<PII> factorization(int N){
vector<PII> factors;
for(int i=0;i<prime.size()&&prime[i]<=sqrt(N);i++){
int cnt=0;
while(N%prime[i]==0){
cnt++;
N/=prime[i];
}
if(cnt)
factors.push_back(make_pair(prime[i],cnt));
}
if(N!=1)factors.push_back(make_pair(N,1));
return factors;
}
質因數分解
- 法3:記得線性篩法的每個合數是被最小的質因數篩掉的嗎?線篩的時候可以記每個合數的最小質因數!這樣質因數分解的時候直接跑迴圈一直除掉最小質因數就好。\(O(lgN)\)
void prime_sieve(){
//...
}
vector<PII> factorization(int N){
vector<PII> factors;
while(N!=1){
int cnt=0,fac=first_prime_factor[N];
while(N%fac==0)
N/=fac,cnt++;
factors.push_back(make_pair(fac,cnt));
}
return factors;
}
群論
二元運算
- 二元運算\((G, \cdot \) )包括兩個部分:
- 1.二元運算子 \( \cdot \)
- 2.集合 \( G\)
- 並且須滿足一個性質:
- 任兩個 \( G\) 裡的元素做完 \( \cdot \) 運算還是\( G\) 裡的元素
- 正式的來說:\( \forall x,y \in G , x \cdot y \in G \)
二元運算
- 1.(\( \mathbb{N}, + \))
- 2.(\( \mathbb{N}, - \))
- 3.(\( \mathbb{N}, \times \))
- 4.(\( \mathbb{Z}, - \))
- 5.(\( \mathbb{Q}, \div \))
- 6.(\( \mathbb{Q^{\times}}, \div \))
- 7.( \(所有可逆矩陣, \times \))
- 8.(\( P^S, \cup \))
- 9.(\( P^S, \cap \))
- 10.(\( P^S, / \) )
哪些是二元運算?
群
- 群是滿足3個性質的二元運算:
- 1.結合律
- 2.存在單位元
- 3.所有元素都存在反元素
結合律
- \( \forall x,y,z \in G, (x \cdot y) \cdot z = x \cdot (y \cdot z)\)
- 三個性質裡最簡單卻最常忽略的一條!
- 試試看證明整數加法和乘法有結合律!
單位元
- \( \exists e \in G, \forall x \in G, x \cdot e = e \cdot x = x\)
- 白話點說,就是要有個元素跟別人算完不會改變他!
- 整數加法的單位元是誰?
- 實數乘法的單位元是誰?
反元素
- \( \forall x \in G, \exists y \in G, x \cdot y = y \cdot x = e\)
- 白話點說,就是要每個人都要有個人可以運算完變回單位元
- 試試看證明每個元素的反元素只會有一個!
- 試試看證明如果\(x\)是\(y\)的反元素,反之亦然!
群
- 1.(\( \mathbb{N}, + \))
- 2.(\( \mathbb{N}, - \))
- 3.(\( \mathbb{N}, \times \))
- 4.(\( \mathbb{Z}, - \))
- 5.(\( \mathbb{Q}, \div \))
- 6.(\( \mathbb{Q^{\times}}, \div \))
- 7.( \(所有可逆矩陣, \times \))
- 8.(\( P^S, \cup \))
- 9.(\( P^S, \cap \))
- 10.(\( P^S, / \) )
哪些是群?
循環群
- 對於任何一個群\(G\),抓出其中一個元素\(g\),可以產生一個\(g\)循環群!群的內容會長這樣:
\(\langle g \rangle \):{\(...,g^{-2},g^{-1},e,g,g^2,...\)} - 如果\(G\)是有限群,那麼\(|G|\)會是\(|\langle g \rangle |\)的倍數!(why?)
- 所以\( g^{|G|} =e \)
- 例子:旋轉的群( {0~3個直角}, +)
- 這個性質等等會用到幾次!
餘數群
同餘符號
- 根據除法原理,對於任何除數和被除數,可以寫成
\(n=qm+r\) ,其中\(n,m,q,r\)分別為被除數,除數,商,餘數
並滿足\(0 \leq r \lt m \) - 如果兩個數\(x,y\)除以\(m\)的餘數一樣,我們可以表示成
\(x \equiv y \;(mod \; m) \)
同餘的運算性質
- 加法律:
\(x \equiv y \;(mod \; m) \)
\(a \equiv b \;(mod \; m) \)
\(\Rightarrow x+a \equiv y+b \;(mod \; m) \) -
乘法律:
\(x \equiv y \;(mod \; m) \)
\(a \equiv b \;(mod \; m) \)
\(\Rightarrow x \times a \equiv y \times b \;(mod \; m) \)
同餘加法群
- 對於任何除數\(m\),他的餘數集合是加法群嗎?
- 首先,他是二元運算嗎?
- 他有結合律嗎?
- 他有單位元嗎?
- 每個餘數都有反元素嗎?
- 我們以\((\mathbb{Z_m} ,+)\)表示\(m\)餘數的加法群
同餘乘法群
- 對於任何除數\(m\),他的餘數集合是乘法群嗎?
- 首先,他是二元運算嗎?
- 他有結合律嗎?
- 他有單位元嗎?
- 每個餘數都有反元素嗎?
- 有沒有反元素,取決於是不是對於每個\(a\),都找得到\(b\)使得
\(ab \equiv 1\; mod \; (m)\)
同餘乘法群
\[ab \equiv 1\; mod \; (m)\]
\[\Leftrightarrow ab=qm+1\]
\[\Leftrightarrow ab+(-q)m=1\]
根據裴蜀定理
\[\Leftrightarrow gcd(a,m)=1\]
同餘乘法群
- 滿足\(gcd(a,m)=1\)的餘數們會構成乘法群
- 換句話說,\(m\)以內跟\(m\)互質的那些數會構成乘法群
- 特別地,如果\(m\)是質數,那0以外的所有餘數都在群裡
- 我們以\((\mathbb{Z_m^{\times}} ,\times)\)表示非零餘數的乘法群(\(m\)須為質數)
費馬小定理
- 若\(p\)是質數,\((\mathbb{Z_p^{\times}} ,\times)\)為乘法群,且群階為\(p-1\)
- 還記得前面講的有限群中的循環群有個性質嗎?
- \( g^{|G|} =e \)
-
此處,\(|G|=p-1, e=1\),並以\(a\)表示任何\(p\)以內的正整數
\[a^{p-1} \equiv 1 \; mod \; p \] - 這就是費馬小定理!
乘法反元素
- 計算某個元素\(a\)在模\(p\)底下的反元素\(a^{-1}\)
- 法一:用裴蜀定理找整數解的方式找反元素
\[ab+qp=1,a^{-1}=b\] - 法二:用費馬小定理
\[a^{p-1} \equiv 1\; mod \; p\]
\[a \times a^{p-2} \equiv 1\; mod \; p\]
\[a^{-1} \equiv a^{p-2} \; mod \; p\]
尤拉定理
- 若\(m\)不是質數,跟\(m\)互質的那些數還是可以構成乘法群,且群階為“\(m\)以內跟\(m\)互質的正整數個數”
- 我們定義一個函數\(\varphi (m)\)為這個個數,稱為尤拉函數
- \( g^{|G|} =e \)
-
此處,\(|G|=\varphi(m), e=1\),並以\(a\)表示任何與\(m\)互質的數
\[a^{\varphi(m)} \equiv 1 \; mod \; m \] - 這就是尤拉定理!費馬小定理是\(m\)為質數的特例
尤拉函數
- 如何計算尤拉函數?
\[\varphi (m)=n \prod_{p|m}^{p \in prime} (1-\frac{1}{p})\] - 找到所有質因數(前面講過!)後直接計算!
- \(10^7\)內質因數最多的數也只有8個,少到不行!
- 注意計算時不要真的用分數算,\(p\)可以除出來
排列組合
各種\(n\)取\(m\)
| 可重複 | 不可重複 | |
|---|---|---|
| 排列 | ||
| 組合 |
排列組合的答案通常很大,會要求模一個質數,後面都假設為\(Q\)!
還有以下範例程式都用int,但排列組合實做一定要用long long !
可重複排列-冪次運算
- 不想從暴力法開始講了,相信大家都學過要用快速冪!
- 這裡提供迴圈版本的快速冪,跑起來比較快
int power(int n,int m){
int num=n,ret=1;
while(m){
if(m%2)ret=ret*num%Q;
num=num*num%Q;
m/=2;
}
return ret;
}
不可重複組合-\(C^n_m\)
- 最泛用的組合數\(C\)!複習一下公式:
\[C^n_m=\frac{n!}{m!(n-m)!}\] - 我們只要討論\(C\)的算法就好,\(P\)跟\(H\)公式大同小異
-
法1:用巴斯卡三角形的轉移式做dp,\(O(N^2)\)
\[C^n_m=C^{n-1}_m+C^{n-1}_{m-1}\] - 複雜度太糟了,我們試試看從公式直接去做
不可重複組合-\(C^n_m\)
- 最泛用的組合數\(C\)!複習一下公式:
\[C^n_m=\frac{n!}{m!(n-m)!}\] - 算完那些東西的階乘,再相除,最後在模\(Q\)!
- 有那麼簡單嗎?階乘很大,是不是過程中就要先模?
- 如果過程中就模了,餘數能直接相除嗎?
- 前面學過乘法群的概念了,在餘數群裡我們不能直接做整數除法,我們要做的事是乘以反元素!
不可重複組合-\(C^n_m\)
- 所以我們要做的事是:
- 1.求\(n!,m!,(n-m)!\)
- 2.求\(m!,(n-m)!\)模\(Q\)的乘法反元素
前面講過方法:裴蜀定理或費馬小定理 - 3.乘在一起再模\(Q\)就是答案了!
- 這樣一次運算是\(O(NlgQ)\),當我們要算很多排列組合時
應該要先把階乘和階乘反元素都預先算好
不可重複組合-\(C^n_m\)
- 預處理\(O(N+NlgQ)\),每次運算\(O(1)\)
int lad[MAX],inv_lad[MAX];
int power(int n,int m){}
int inv(int a){
return power(a,Q-2);
}
void preprocess(){
int i;
lad[0]=inv_lad[0]=1;
for(i=1;i<MAX;i++){
lad[i]=lad[i-1]*i%Q;
inv_lad[i]=inv_lad[i-1]*inv(i)%Q;
}
}
int C(int n,int m){
return lad[n]*inv_lad[m]%Q*inv_lad[n-m]%Q;
}
不可重複組合-\(C^n_m\)
- 讓我們更進一步把\(O(lgQ)\)壓掉!
反元素有一個遞推公式可以用:
\[inv(n)=(Q-Q/n) \times inv(Q\%n) \%Q\] - 這樣可以\(O(1)\)用已知的答案推到現在的答案!
- 這個公式的證明不難,只有用到餘數定理,可以自己試試看
不可重複組合-\(C^n_m\)
- 預處理\(O(N)\),每次運算\(O(1)\)
int lad[MAX],inv_lad[MAX],inv[MAX];
void preprocess(){
int i;
lad[0]=lad[1]=inv_lad[0]=inv_lad[1]=inv[1]=1;
for(i=1;i<MAX;i++){
lad[i]=lad[i-1]*i%Q;
inv[i]=(Q-Q/i)*inv[Q%i]%Q;
inv_lad[i]=inv_lad[i-1]*inv[i]%Q;
}
}
int C(int n,int m){
return lad[n]*inv_lad[m]%Q*inv_lad[n-m]%Q;
}更多排列組合!
高中排列組合從不提的
- 排列:就算元素一樣,只要順序不同就算不同
- 組合:只要元素一樣,不管順序如何都算相同
- 真的只有這兩種狀況嗎?
- 同時有"某種順序不同算一樣"和“某種順序不同算不同”的?
- 題目:有一個正方形,我們要將四個頂點著上黑或白色,旋轉後相同的塗色法算是同一種,請問有幾種塗法?
- 列舉法可得正確答案是6種:
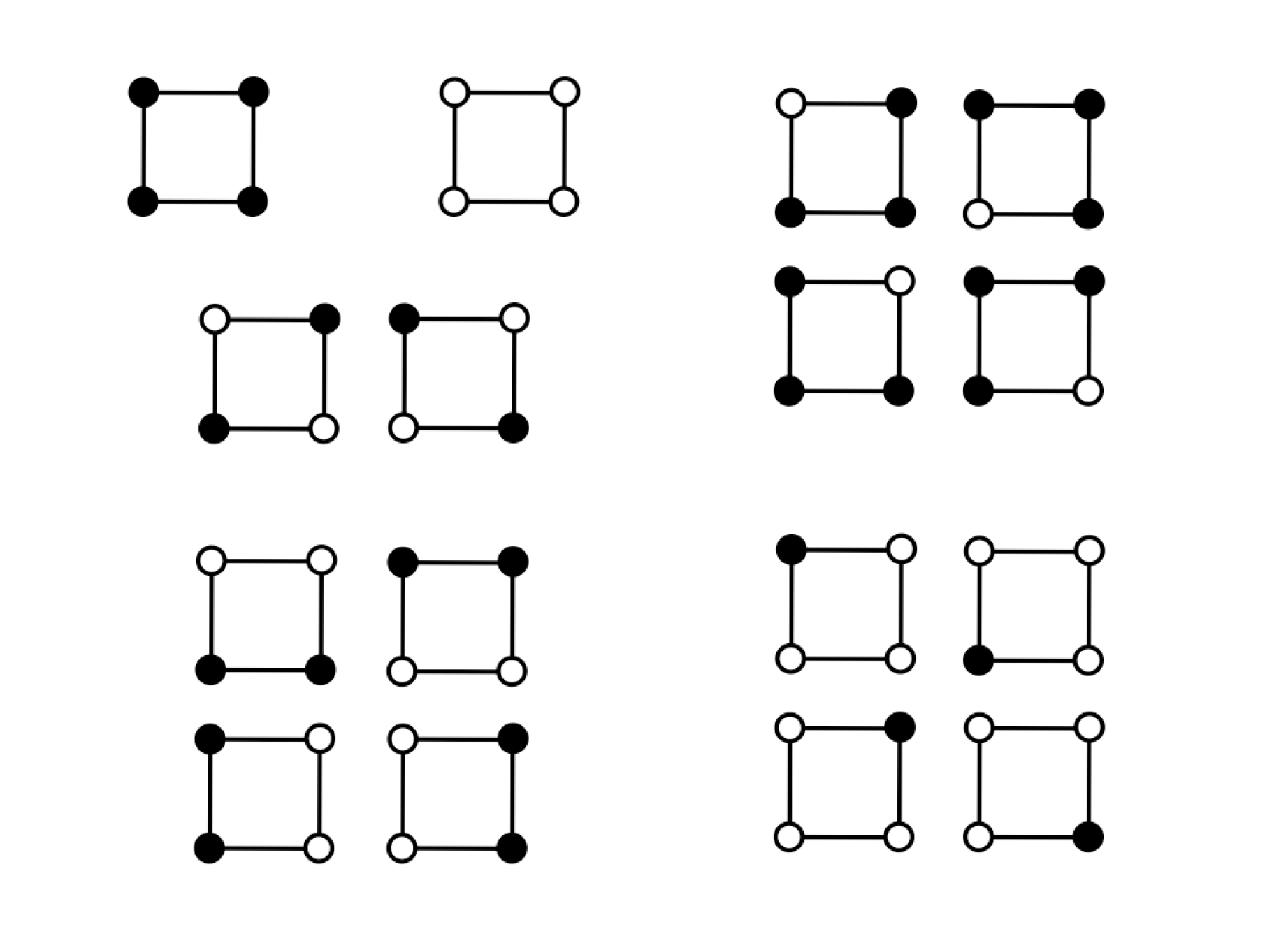
- 排列數會得到\(2^4=16\)種,錯在旋轉後的只能算一種
- 組合數會得到\(H^2_4=5\)種,錯在2黑2白有兩種可能
- 這種題目除了列舉,還有什麼方式算呢?

Burnside Lemma
- 令所有(作用完只能算同一種)的作用集合為群\(G\)
以剛剛那題來說,就是4種旋轉 - 令所有的排列可能為集合\(X\)
以剛剛那題來說,就是那16種排列 - 令集合\(X_g\)為,\(X\)中受到\(G\)中作用\(g\)後,長得一模一樣的那些元素\(x\)的集合
- 總共的種類數,就是每個\(|X_g|\)的平均!
Burnside Lemma
- 以剛剛那題而言群\(G=\{ r0,r1,r2,r3\}\)分別代表轉0~3次
(說明看看這為什麼是群?結合律?單位元?反元素?) - 集合\(X\)是:
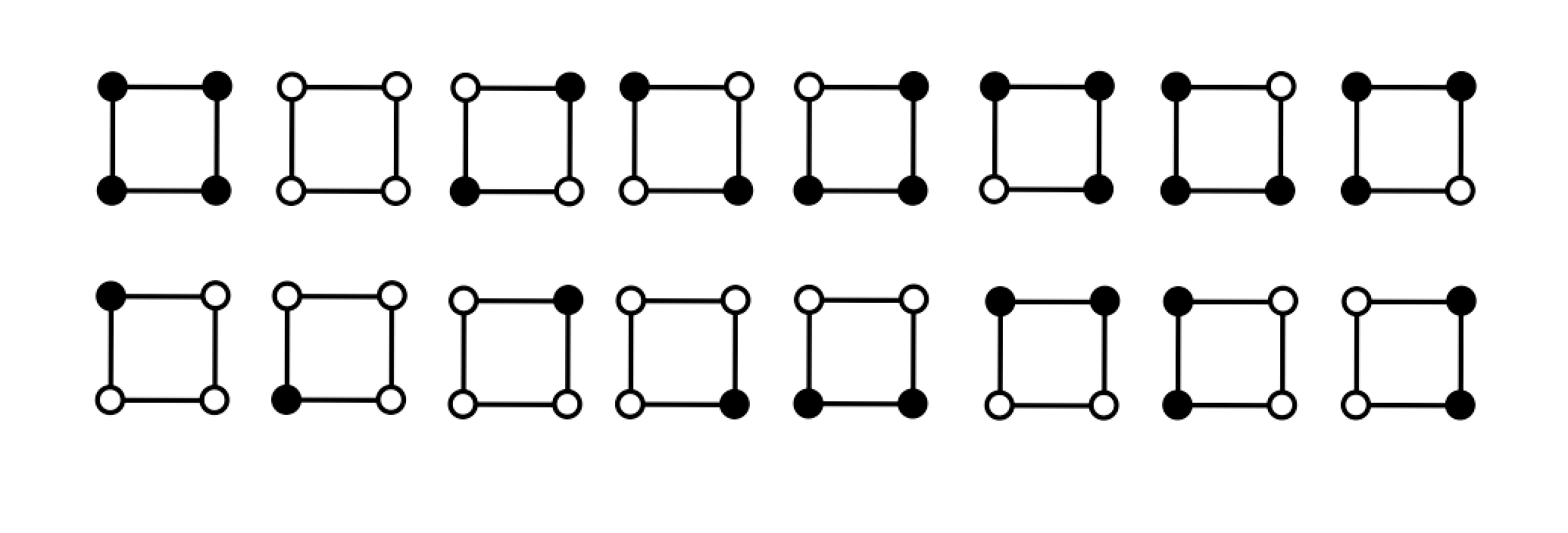
Burnside Lemma
- 集合\(X_{r0}\)是順時針轉0次後長得一樣的那些元素
顯然是所有的排列,所以\(|X_{r0}|=16\)

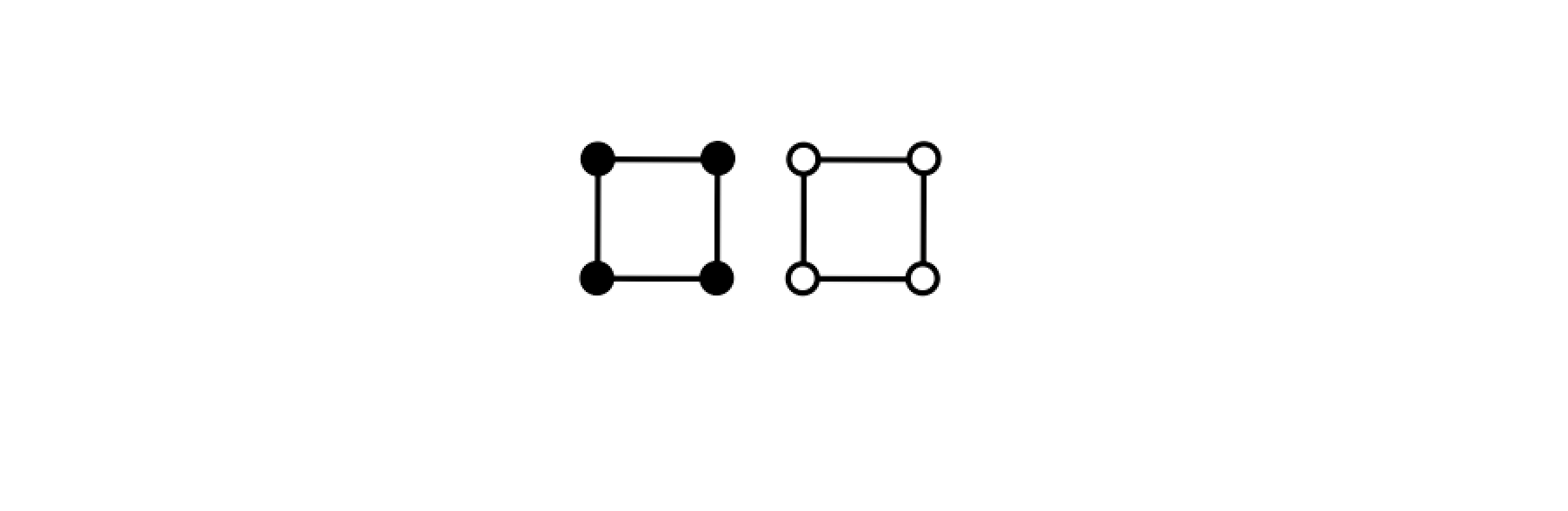
Burnside Lemma
- 集合\(X_{r1}\)是順時針轉1次後長得一樣的那些元素
只有下面這兩種排列,所以\(|X_{r1}|=2\)
Burnside Lemma
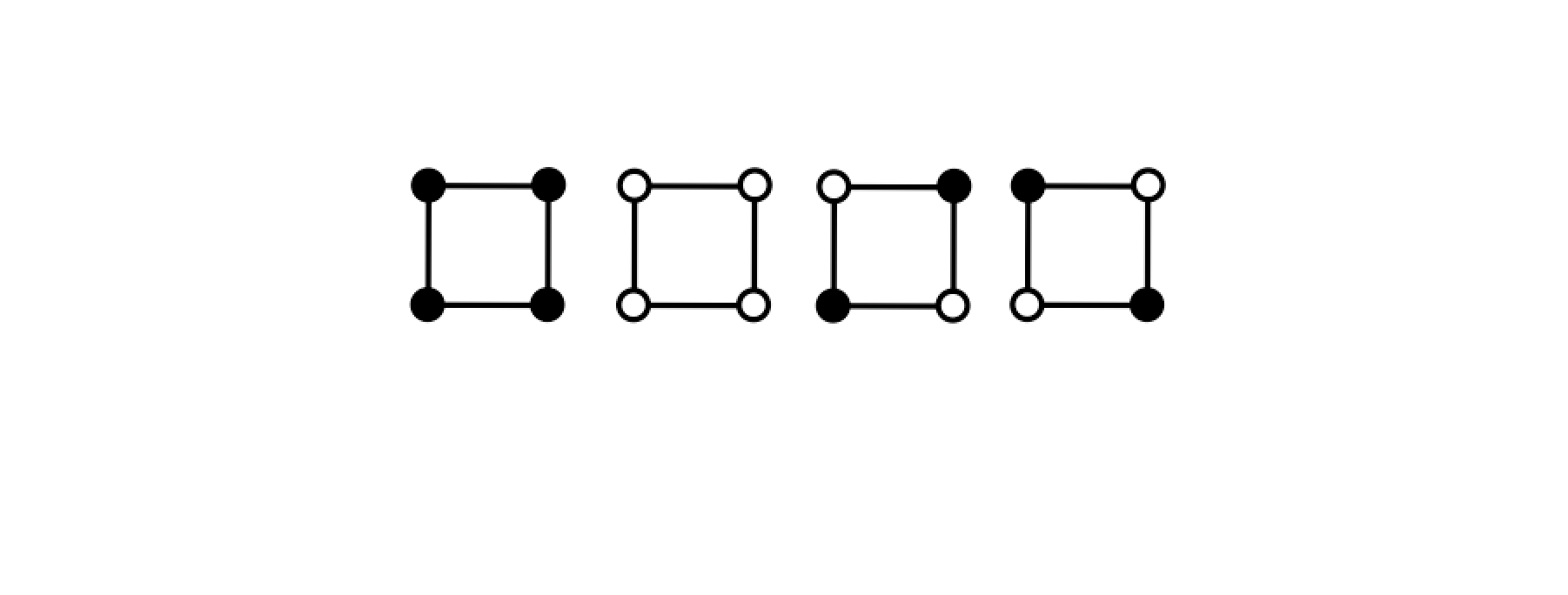
- 集合\(X_{r2}\)是順時針轉2次後長得一樣的那些元素
有下面這幾種排列,所以\(|X_{r2}|=4\)
Burnside Lemma
- 集合\(X_{r3}\)是順時針轉3次後長得一樣的那些元素
只有下面這兩種排列,所以\(|X_{r3}|=2\)

Burnside Lemma
- 所以總共的方法數就是剛剛那4個集合大小的平均
\[\frac{16+2+4+2}{4}=6\] - 跟一開始列舉法的答案一樣!
Burnside Lemma
- 最後我們把剛剛的算法寫成公式,
這就是Burnside Lemma!
\[N=\frac{1}{|G|}\sum^{g \in G}_g{|X_g|}\] - 其實就是個算平均數的公式而已!
Burnside Lemma
- Bonus題:有1藍,2紅,2綠,3黃的珠子,要串成一環手鏈
有幾種串法?(既然是手鍊,所以旋轉翻轉相同的都算一樣)
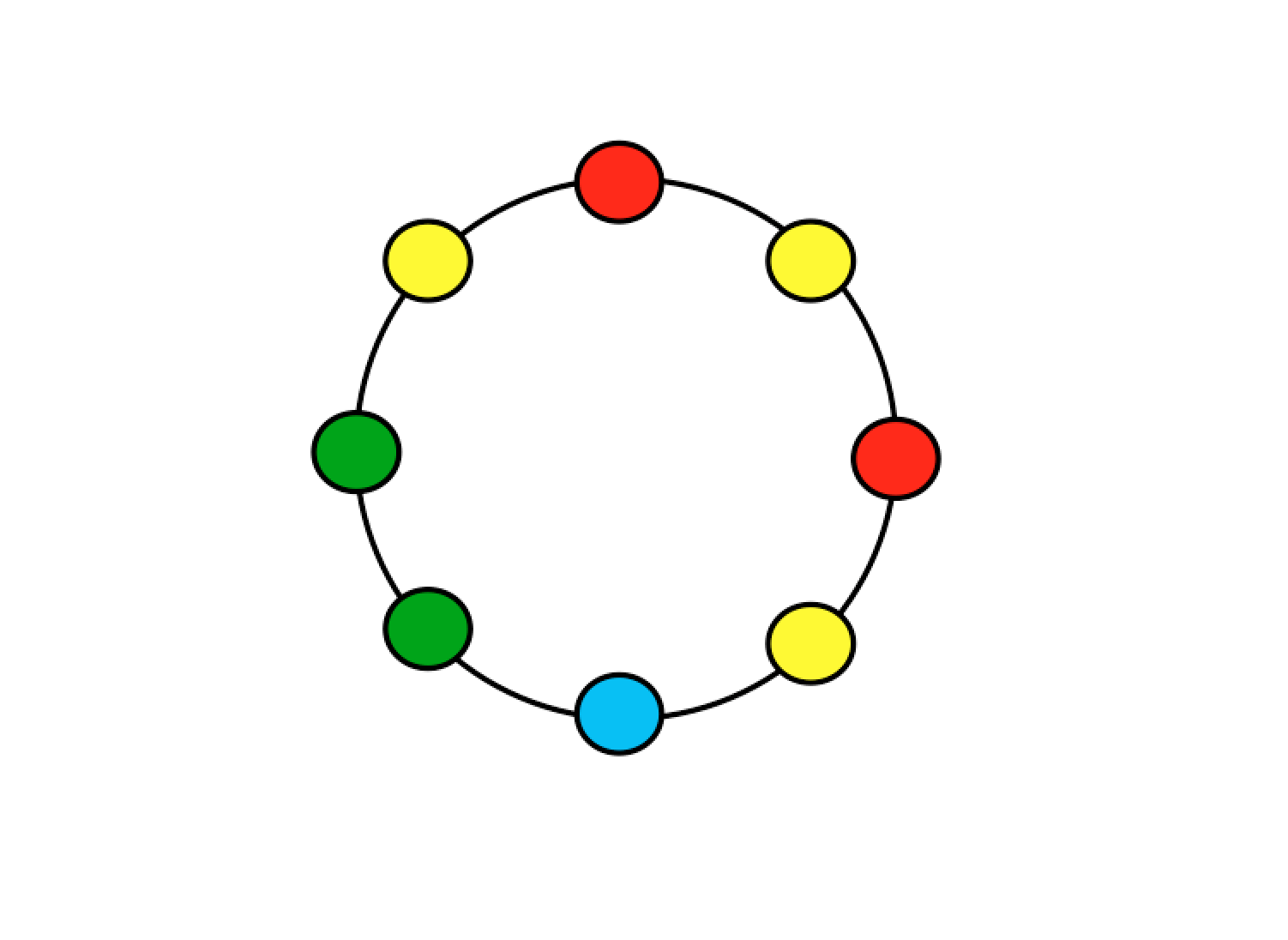
最後,來學點實用的東西!
密碼學
密碼學
- 密碼學的內容,主要就是關於如何傳遞秘密
- 在現實生活中,我們怎麼傳遞秘密給朋友?
密碼學
- 到他身邊單獨跟他講,就沒人聽得到了!
- 網路世界讓我們可以跟遠方的人對談
- 如果要傳遞秘密給遠方的人呢?這個方法是不是沒用了?
- 我們可以把訊息加密後再傳遞!
加密的方法
- 首先,我們知道不論中英文訊息都可以轉換成數字信號
- 所以以下討論的加密解密都直接把秘密當作一個數字!
- 傳遞方可以事先跟接收方約定好數字\(a,p\)
- 假如要傳遞的數字是\(m\),傳遞方傳出\(a \times m\)
- 接收方計算模\(p\)底下\(a\)的反元素\(a^{-1}\)(記得怎麼算嗎?)
- 接收方計算\(a \times m \times a^{-1} mod\; p\),就是原本的\(m\)!
- 不知道\(a\)跟\(p\)的外人,無法計算\(a^{-1}\)!
共同秘密
- 現在問題變簡單了,只要有辦法跟遠方的人隨意約定數字
就能用剛剛的方法傳遞任何秘密訊息! - 只是問題還沒消失,要隨意約定一個數字,不也是要傳遞秘密嗎?
- 但這個秘密比較簡單,因為並不是一個特定的數字,只要雙方能產生一個有共識,且其他人不知道的數字就好。
共同秘密
- 怎麼做到這件事呢?
- 來假設一個情境,你跟你朋友和一個陌生人在一個房間裡
- 你要跟你朋友在房間裡的對談中產生一個共識的數字
- 規則:你們講話的任何內容,陌生人都聽的到
- 開放大家思考,你跟你朋友會怎麼做!
共同秘密
- 因為他是你朋友,所以用隨意一個兩人的共同秘密就好!
- 想一些你朋友會知道,陌生人不會知道的
- 例:你的生日數字和,班上某個同學的座號,...
- 因為記得,這個數字是什麼都沒關係,兩人有共識就好!
共同秘密
- 現在剩下一個問題
- 如果要向陌生人傳遞秘密呢?
- 那我們需要和陌生人取得共同秘密
- 有沒有可以憑空讓兩人產生共同秘密的演算法?
共同秘密
- 構思:
- 我們找一種運算\( \cdot \)
- 這種運算要有交換律但不能有反元素(或是難以找到)
- 這樣甲方可以先念出一個數字A,然後叫乙方跟自己各別暗自想一個數字B跟C
- 甲方唸出\(A \cdot B\),乙方唸出\(A \cdot C\)
- 兩人就都可以算出\(A \cdot B \cdot C\)
- 丙方只有聽到\(A\), \(A \cdot B\), \(A \cdot C\),算不出\(A \cdot B \cdot C\)!
共同秘密
- 假想但是好理解的其中一個方法:
- 我們把共同秘密從數字改成顏色,且三人都有三原色塗料
- 混色即是一種滿足剛剛性質的運算!
- 混色順序沒有影響(有交換律),且反元素不好找(咖啡-粉=?)
- 甲混出一個任意顏色A放在房間中間
- 甲跟乙各暗自混出一個顏色B和C,並混出AB色和AC色放出來
- 甲跟乙現在都可以暗自混出ABC色了!但丙混不出來!
共同秘密
- 當然這只是讓大家好理解的假想,實際上顏色當秘密沒什麼用
- 我們還是得來介紹適用於數學的演算法!
Diffie-Hellman Key Exchange
- 甲方公布底數\(g\)和模數\(p\)
- 甲方跟乙方各暗自想一個數字\(a\)和\(b\)
- 兩人計算並公布數字\(A=g^a mod\; p,B=g^b mod\; p\)
- 現在甲跟乙可以各自計算
\(K=A^b mod\; p=B^a mod\; p=g^{ab} mod\; p\) - \(K\)便可以當作兩人的共同秘密!
- 丙需要用\(A=g^a mod\; p\)解\(a\),必須窮舉\(p\)以內所有次方,因此甲只要選一個超大的質數就好
- 事實上解同餘對數有\(\sqrt{N}\)的算法,但還是太慢
Diffie-Hellman Key Exchange
- 疑問:怎麼樣算夠快,怎麼樣算太慢?
- “選一個超大的質數就好”,這件事夠快嗎?
- “解同餘對數有\(\sqrt{N}\)的算法”,為什麼算太慢?
- 多項式時間 vs 非多項式時間
- 如果P=NP呢?
- If P = NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in "creative leaps," no fundamental gap between solving a problem and recognizing the solution once it's found. Everyone who could appreciate a symphony would be Mozart; everyone who could follow a step-by-step argument would be Gauss; everyone who could recognize a good investment strategy would be Warren Buffett.
質數的密度&檢驗法
- \(n\)以內的質數密度為\(\frac{1}{\ln n}\)
- Miller Rabin質數判定法:
- 令\(n-1=2^sd\)
- 任意選擇一個\(a<n\)
- 若\(a^d \mod n \ne 1\)且對於所有\(0 \leq r \leq s - 1\), \(a^{2^rd} \mod n \ne -1\),\(n\)為合數
- 否則,\(n\)有\(\frac{3}{4}\)的機率為質數
加密的方法
- 傳遞方可以事先跟接收方約定好數字\(a,p\)
- 假如要傳遞的數字是\(m\),傳遞方傳出\(a \times m\)
- 接收方計算模\(p\)底下\(a\)的反元素\(a^{-1}\)(記得怎麼算嗎?)
- 接收方計算\(a \times m \times a^{-1} mod\; p\),就是原本的\(m\)!
- 不知道\(a\)跟\(p\)的外人,無法計算\(a^{-1}\)!
- 這頁剛剛出現過,現在我們會製造共同秘密,就能實行了!
欲求不滿
- 剛剛學的那種加密法叫做對稱式加密
- 雙方先進行製造共同金鑰(秘密),然後可以平等的用這個金鑰進行大量的資訊交換
- 問題1:只要一方的私鑰被竊,竊取者就可以計算共同金鑰,進而將後續所有訊息將可以被外人獲取,所以對稱式加密涉及金鑰管理的問題
- 問題2:若有人假冒成甲方跟乙方進行共同金鑰的交換,並進行接下來的資訊交流,乙方無從得知(中間人攻擊)
非對稱式加密
- 先解決第一個問題,我們想辦法把剛剛的加密演算法修正成由接受訊息(甲方)公布加密方法與常數,乙方只要加密就好(不用產生自己的私鑰),然後傳遞加密過的訊息,甲方再解密
- 這樣所有演算法的負擔都落在甲身上就好,乙只要照著加密
- 需要能保證只有甲方知道要怎麼解密!
加密的方法
- 甲方公布數字\(a,p\)
- 假如要傳遞的數字是\(m\),乙方傳出\(a \times m\)
- 甲方計算模\(p\)底下\(a\)的反元素\(a^{-1}\)
- 甲方計算\(a \times m \times a^{-1} mod\; p\),就是原本的\(m\)!
- 問題大的很!\(a,p\)都公佈了外人不就也可以算\(a^{-1}\)?
- 我們稍做調整,把乘法改成次方運算看看
加密的方法
- 甲方公布數字\(a,p\)(\(p\)是質數)
- 假如要傳遞的數字是\(m\),乙方傳出\(m^a\)
- 甲方計算模\(\varphi(p)\)底下\(a\)的反元素\(a^{-1}\)
- 為什麼是模\(\varphi(p)\)?
- 甲方計算\((m^a)^{a^{-1}} mod\; p=m^1 mod \; p\),就是原本的\(m\)!
- 還是有問題!\(a,p\)都公佈了,\(\varphi(p)\)不就是\(p-1\)嗎?外人不就也可以算\(a^{-1}\)和\(m^{a^{-1}}\)?再改進一下!
加密的方法
- 模數不要是質數,改成兩個質數相乘!
- 甲方選兩個質數\(p,q\),相乘得到\(n\)
- 甲方公布數字\(a,n\)(a與n互質)
- 假如要傳遞的數字是\(m\),乙方傳出\(m^a\)
- 甲方計算模\(\varphi(n)\)底下\(a\)的反元素\(a^{-1}\)
- 甲方計算\((m^a)^{a^{-1}} mod\; n=m^1 mod \; n\),就是原本的\(m\)!
- \(\varphi(n)=(p-1)(q-1)\) (為什麼?)
加密的方法-RSA
- \(\varphi(n)=(p-1)(q-1)\)
- 甲很快就算出來了,但是外人不知道\(p,q\),而要從\(n\)分解出\(p,q\)必須要作質因數分解,需要\(\sqrt{n}\)的時間!
(記得嗎?沒有質數表時質因數分解是\(\sqrt{n}\)) - 甲只要選兩個很大的質數就好了!
- 同樣的,這裡的夠不夠快之別,前面討論過了
- 這個算法就是鼎鼎大名的RSA演算法!
加密的方法-RSA
- 回憶一下前面提到對稱式加密的缺點
- 我們來看看第二個如何解決:
對稱式加密中收方沒辦法驗證發方資訊 - 這是很嚴重的問題,任何惡意軟體都能冒名自己的正統性
- 剛剛的RSA算法修一下就能變成一個用來驗證訊息一定是甲送出的演算法!
加密的方法
- 甲方選兩個質數\(p,q\),相乘得到\(n\)
- 甲方公布數字\(n\)
- 甲方選一個數字\(a\)(a與n互質)
- 甲方計算並公佈數字\(a^{-1}\)(模\(\varphi(n)\)底下\(a\)的反元素)
- 假如要傳遞的數字是\(m\),甲方傳出\(m^a\)
- 所有外人都能計算\((m^a)^{a^{-1}} mod\; n\)就是原本的\(m\)!
加密的方法
- 所有外人都能計算\((m^a)^{a^{-1}} mod\; n\)就是原本的\(m\)!
- 大家都能解密,但是只有甲方能加密!(不是甲方的人無法製造一對反元素\(a,a^{-1}\)),因為其他人不知道\(\varphi(n)\))
- 解密成功的大家都能確定訊息一定是甲方發的!
- 這種技術叫做數位簽章,RSA算法竟然一次解決對稱式算法的兩個缺點!
兩全其美
- 我們看到了非對稱式可以解決對稱式算法的兩個缺點
- 對稱式算法有沒有缺點?
- 有,太不方便了!傳送一個數字要作的運算太複雜
- 實務上可以對稱式加非對稱式一起用!
- 先用非對稱式算法產生暫時的共同金鑰,並用那個金鑰進行大量的對稱式資訊傳遞,又快又安全
現在大家都是數論高手了!
結論
- 數論從最純的數學開始,解釋很多我們習以為常的事
- 卻是密碼學的基石,而密碼學可是深深影響日常生活跟戰爭的重要知識呢!
- 各種數論演算法也會在奧林匹亞競賽裸著出現或是藏在其他領域的題目中!
deck
By Howard Yang
deck
- 204



