NSLab
Paper Presentation
B06902097 資工三 楊皓丞
這學期主要做的研究
- Anonymous Authentication Protocols:
- Direct Anonymous Attestation (DAA)
- Group Signatures
- Ring Signatures
- Their applications on wifi authentication
- Anonymous Communication (AC) Protocols:
- 後來有空有興趣就看了一些這方面的paper
- Tor, Mix net, DC net, ...
- 今天要報一篇關於AC protocol性質的paper
Topic
- Anonymity Trilemma:
- Strong Anonymity
- Low Bandwidth Overhead
- Low Latency Overhead
- Choose two!
Reference: D. Das, S. Meiser, E. Mohammadi, and A. Kate, “Anonymity trilemma: Strong anonymity, low bandwidth overhead, low latency—choose two,” Proceedings of IEEE S&P 2018 (to appear), San Francisco, CA, USA, May 2018. Available: https://eprint.iacr.org/2017/954
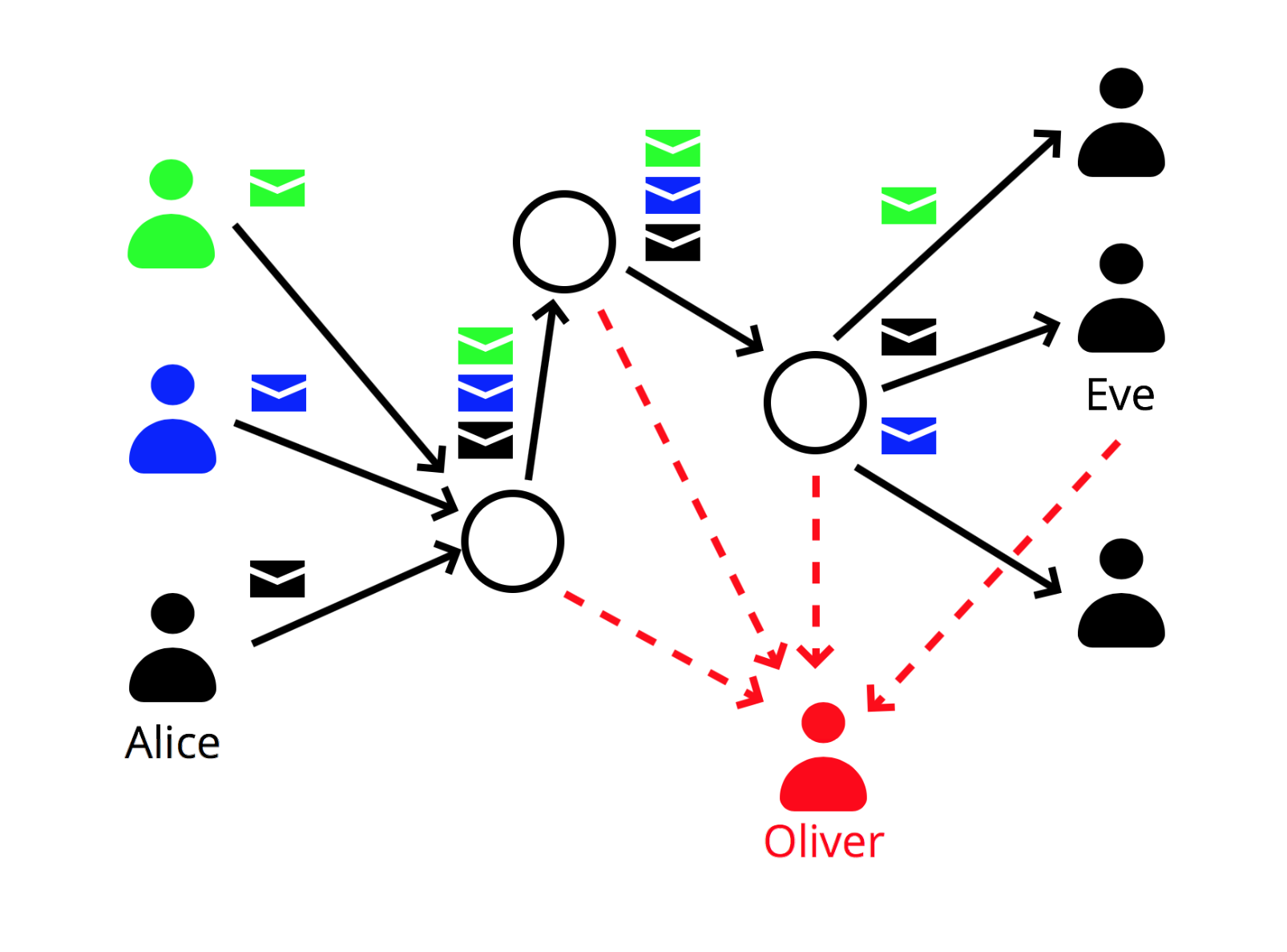
AC Networks
Alice
Eve
Oliver
Anonymous set
Example
Alice
Eve
Oliver
Low Anonymity
High Anonymity
The Trilemma
- Given the user behavior, either:
- Accept low anonymity
- Increase latency overhead
(wait for messages) - Increase bandwidth overhead
(produce dummy messages)
Anonymity Trilemma
Strong Anonymity
Low Bandwidth Overhead
Low Latency Overhead
mix-nets
DC-nets
Tor
Can we achieve this?
No
Aim of the paper
- State that there's a tradeoff among anonymity \(\delta\) , latency overhead \(l\), and bandwidth overhead \(\beta\).
- Give the constraints of the parameters \(\delta, l, \beta\), for protocol designers to consider.
- Give the constraints of the parameters \(l, \beta\) that must hold to achieve strong anonymity, for protocol designers to consider.
Definitions - Anonymity
- AnoA style challenge response game
- \(\delta \ge 0\) is the advantage of the attacker
- \(\delta\) is a function of \(\eta\), the security parameter
- \(\Pr(\text{Attacker wins}) \le \Pr(\text{Attacker loses}) + \delta(\eta)\)
- Strong anonymity: \(\delta(\eta) = neg(\eta)\)
Alice
Eve
Oliver
Bob
Alice or Bob?
Definitions - Latency
- One time unit = One communication round
- \(l\) is the maximum number of rounds the message can stay in the network before being delivered
- In this example, \(l=3\) if the routers always forward messages the next round after receiving them
Alice
Eve
Definitions - Bandwidth
- \(\beta\) is the average number of dummy messages that needs to be sent per user per round
- In this example, \(\beta=\frac{2}{N}\) if the blue and green arrows are two users assigned to send one dummy message this turn, and there are \(N\) users in total.
Alice
Eve
Scenarios Discussed
- User behavior
- Synchronized: over \(N\) rounds, exactly one user per round sends a message, and each user sends once
- Unsynchronized: in each round, each user sends a message with probability \(p\)
Scenarios Discussed
- Attacker capability
- Global passive: monitors all the message flows, but cannot see the content of the message except at compromised nodes
- Attacker compromised the receiver and \(c\) out of \(K\) protocol parties
- Non-compromising attacker: \(c = 0\)
- Compromising attacker: \(c > 0\)
Scenarios Discussed
- For each scenario, the paper gives two sets of constraints:
- The inequalities of \(\delta, l, \beta\)
- The inequalities of \(l, \beta\) to achieve strong anonymity
- Necessary conditions, not sufficient conditions.
- We focus on synchronized, non-compromising attacker scenario, the others are of similar logic
| Non-compromising | Compromising | |
| Synchronized | ||
| Unsynchronized |
Most simple!
Proof Outline
- Derive a lower bound on attacker advantage \(\delta\)
- For a protocol \(\prod\), \(\delta\) is the greatest advantage of all attackers \(A \in Attackers\)
- Which is bounded by the advantage of a specific attacker \(A_{paths}\)
- Which is bounded by \(\Pr(\text{Invariant 1 is true})\)
- Which is bounded by \(\min(\Pr(\text{Invariant 1 is true}))\) among all protocols with parameters \(l, \beta\)
- Which can be expressed as an inequality
- Derive a necessary condition for strong anonymity, using the bound derived above
Construction of \(A_{paths}\)
Alice
Eve
Bob
Alice!
Construction of \(A_{paths}\)
Alice
Eve
Bob
I don't know...
Construction of \(A_{paths}\)
Alice
Eve
Bob
if \(l=4\):
I don't know...
if \(l=3\):
Alice!
Construction of \(A_{paths}\)
- \(A_{paths}\) simply checks reachability based on \(l\) and the network structure
- If it is impossible that either Alice or Bob send the message, \(A_{paths}\) wins with probability 1
- Else, it flips a coin and guess Alice or Bob and wins with probability 0.5
- \(A_{paths}\) only checks reachability, it does't analyze whether Alice or Bob is more likely to send the message if both are possible
Invariant 1
- Let \(u_0, u_1\) be the challenged users
- \(u_b\) is the real user sending the challenge message
- The challenge message is sent at \(t_0\) by \(u_b\)
- The challenge message is received at time \(r\)
- \(u_{1-b}\) sent messages at time \(V=\{t_1, t_2, ..., t_k\}\)
- Let \(T=\{t:t \in V \land (r-l) \le t < r\}\)
Invariant 1
- \(u_{1-b}\) sent messages at time \(V=\{t_1, t_2, ..., t_k\}\)
- Let \(T=\{t:t \in V \land (r-l) \le t < r\}\)
- Then (Invariant 1 is true) is defined as the event that
- \(T \ne \phi\), and
- The challenge message passed through a not compromised node at time \(t'\), where
\(\min(T) \le t' \le r - 1\)
Invariant 1
\(r\)
\(t_1\)
\(t_2\)
\(t_0\)
\(t_3\)
\(t_4\)
\(t_5\)
\(r-l\)
Alice sends
Eve receives
Bob sends a message inside this interval
Challenge message passes through a honest node in this interval
If Invariant 1 doesn't hold, \(A_{paths}\) wins with probability 1
Derive the probability
- Synchronized and non-compromising case
- \(H_1\): In the \(l\) rounds, \(u_{1-b}\) sends at least one noise message
- \(H_2\): In the \(l\) rounds, \(u_{1-b}\) sends his user message
- \(H_3\): Invariant 1 is true \(\equiv (T \ne \phi) \equiv (H_1 \lor H_2)\)
Derive the probability
- \(H_2\): In the \(l\) rounds, \(u_{1-b}\) sends his user message
- \(\Pr(H_2) \le \frac{l-1}{N-1}\)
- \(H_1\): In the \(l\) rounds, \(u_{1-b}\) sends at least one noise message
- \(\Pr(H_1) \le \frac{\beta N l}{N-1}\)
- \(H_3\): Invariant 1 is true \(\equiv (T \ne \phi) \equiv (H_1 \lor H_2)\)
- \(\Pr(H_3) = \Pr(H_1 \lor H_2) \le \min(1, \Pr(H_1) + \Pr(H_2))\\ \Pr(H_3) \le \min(1, \frac{l+\beta N l}{N-1})\)
Derive the constraint - 1
- \( \Pr(H_3) \le \min(1, \frac{l+\beta N l}{N-1})\)
- Let \(f_\beta(l)=\min(1,\frac{1+\beta N l}{N - 1})\)
- Since \(A_{paths}\) wins with probability \(P \ge\)
\(\Pr(H_3) \times 0.5 + (1 - \Pr(H_3)) \times 1=1+0.5\Pr(\lnot H_3)\) -
\(A_{paths}\)'s advantage \(\delta \ge \Pr(\lnot H_3) \ge 1-f_\beta(l)\)
- Any protocol must satisfy \(\delta \ge 1-f_\beta(l)\)
Derive the constraint - 2
- \(\delta \ge 1-f_\beta(l)\)
- \(\delta(\eta) \ge \frac{N-l-\beta N l}{N-1} \ge 1 - \frac{l}{N} - \beta l\)
- Assume that \(\delta(\eta) =neg(\eta)\) and \( 2l\beta < 1 - \epsilon(\eta)\)
- By \(\epsilon(\eta) > \delta(\eta)\), we can derive that if \(l < N\), there must be a contradiction that \(\epsilon(\eta) < \delta(\eta)\)
- Any protocol with \(l<N\) and \( 2l\beta < 1 - \epsilon(\eta)\) cannot achieve strong anonymity
Derive the constraint
- Any protocol must satisfy \(\delta \ge 1-f_\beta(l)\)
-
Any protocol with \(l<N\) and \( 2l\beta < 1 - \epsilon(\eta)\) cannot achieve strong anonymity
- In unsynchronized case, if user sends message \(p\) of the time, strong anonymity cannot be achieved if
\( 2l(\beta+p) < 1 - \epsilon(\eta)\) - Constraints of other scenarios use similar proof techniques
Cases
- \(l=N,\beta=0\): possible
Alice
Eve
Bob
I don't know...
Carol
Cases
- \(l=\frac{N}{3},\beta=\frac{3}{N}\): possible
Alice
Eve
Bob
I don't know...
Carol
Cases
- \(l=1,\beta=\frac{1}{2}\): impossible,
although constraint holds
Alice
Eve
Bob
If \(u_0\) or \(u_1\) is Carol, I win
Carol
Non-negligible
advantage!
Results
\(l\)
\(\beta\)
mix-net
Tor
DC-net
\(O(N)\)
\(O(1)\)
\(O(\frac{1}{N})\)
grey area: \(2l\beta < 1 - \epsilon\)
no strong anonymity
\(O(1)\)
Takeaways & Thoughts
- When designing AC protocols, there will always be a trilemma between anonymity, latency, and bandwidth
- The constraints are necessary conditions, and I think the bounds are too loose
- Maybe tighter bounds can be derived
- User behavior (message sending rate) can compensate for bandwidth, so is the trilemma really unavoidable?
Questions?
Paper Presentation
By Howard Yang
Paper Presentation
- 104



