Learning Latent Dynamics
with Informative Constraints
SIAM: Operator Learning in the Physical and Data Sciences
Assoc. Prof. Efstratios Gavves,
University of Amsterdam
PhD Ilze Amanda Auzina
University of Amsterdam
Dr. Çağatay Yıldız,
University of Tuebingen
Tuebingen AI Center
Learning Latent Dynamics
with Informative Constraints
To interact with the physical world...
Latent
Learning Latent Dynamics
with Informative Constraints
To interact with the physical world...
...we need to model it correctly
Latent Dynamics
Dynamics
\dot{\mathbf{x}}(t) := \frac{d\mathbf{x}(t)}{dt} = \mathbf{f}(t, \mathbf{x}(t))
\mathbf{x}(t_{1}) = \mathbf{x}(t_{0}) + \int_{t_{0}}^{t_{1}} \mathbf{f}(\mathbf{x}(\tau))d\tau
Latent Dynamics
Generative Model
Dynamics
\dot{\mathbf{x}}(t) := \frac{d\mathbf{x}(t)}{dt} = \mathbf{f}(t, \mathbf{x}(t))
\mathbf{x}(t_{1}) = \mathbf{x}(t_{0}) + \int_{t_{0}}^{t_{1}} \mathbf{f}(\mathbf{x}(\tau))d\tau
Generative Process
\mathbf{z}_{1} \sim p(\mathbf{z}_{1}) \\
\mathbf{z}_{i} =\mathbf{z}_{1} + \int_{t_{i}}^{t_{i}} \mathbf{f}_{\theta}(\mathbf{z}(\tau))d\tau \\
\mathbf{x}_{i} \sim p_{\xi} (\mathbf{x}_{i} | \mathbf{z}_{i})
Fig.1. Latent Neural ODE model (Chen et al., 2018)
\mathbf{x}_{t} = A \text{sin}(2\pi f t + \phi)
Inference
Latent Neural ODE model (Chen et al., 2018)
Benefit: NN can learn any function
Limitation: NN can learn any function
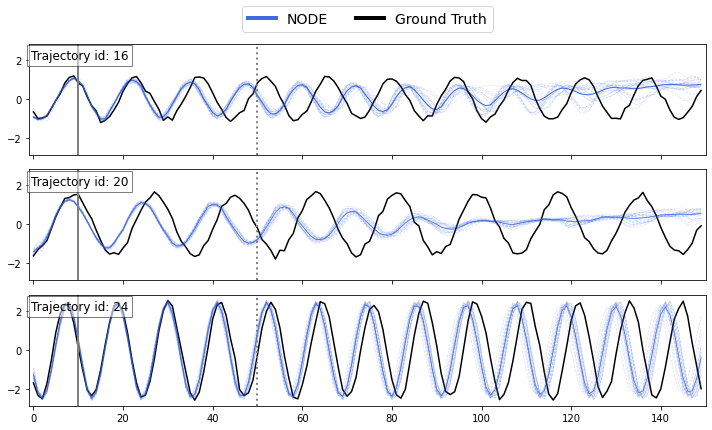
Fig. 2. Latent NODE forecasting on sinusoidal sequences
Fig. 3. PCA embeddings of latent sinusoidal trajectories
Latent ODE with Constraints and Uncertainty
Gaussian Process
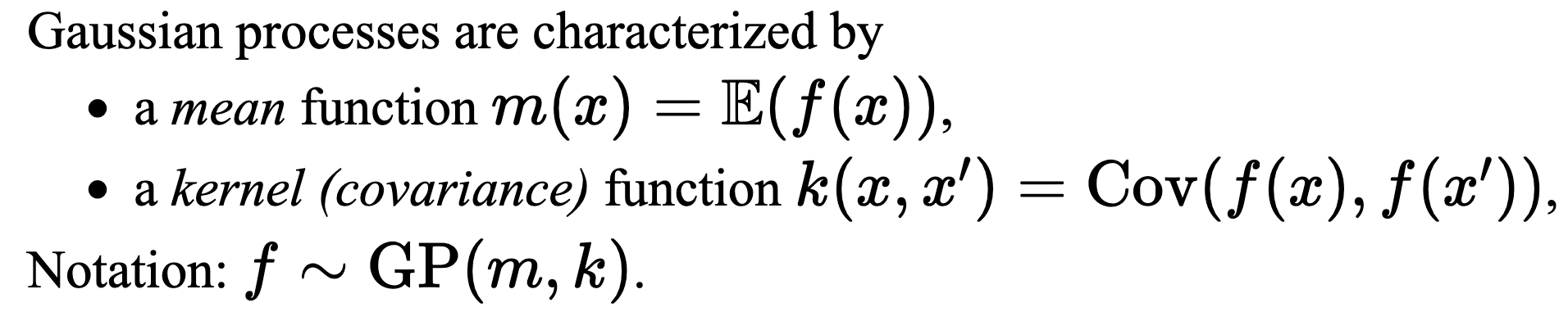
Credits: Johan Wagberg, Viacheslav Borovistkiy
Gaussian Process ODE
\dot{\mathbf{x}_{t}}:= \frac{d\mathbf{x}_{t}}{dt} = \mathbf{f}( \mathbf{x}_{t})
\mathbf{f}(\mathbf{x}) \sim GP (\mathbf{0}, K(\mathbf{x},\mathbf{x}')),
K(\mathbf{x},\mathbf{x}') \in \mathbb{R}^{D\times D}
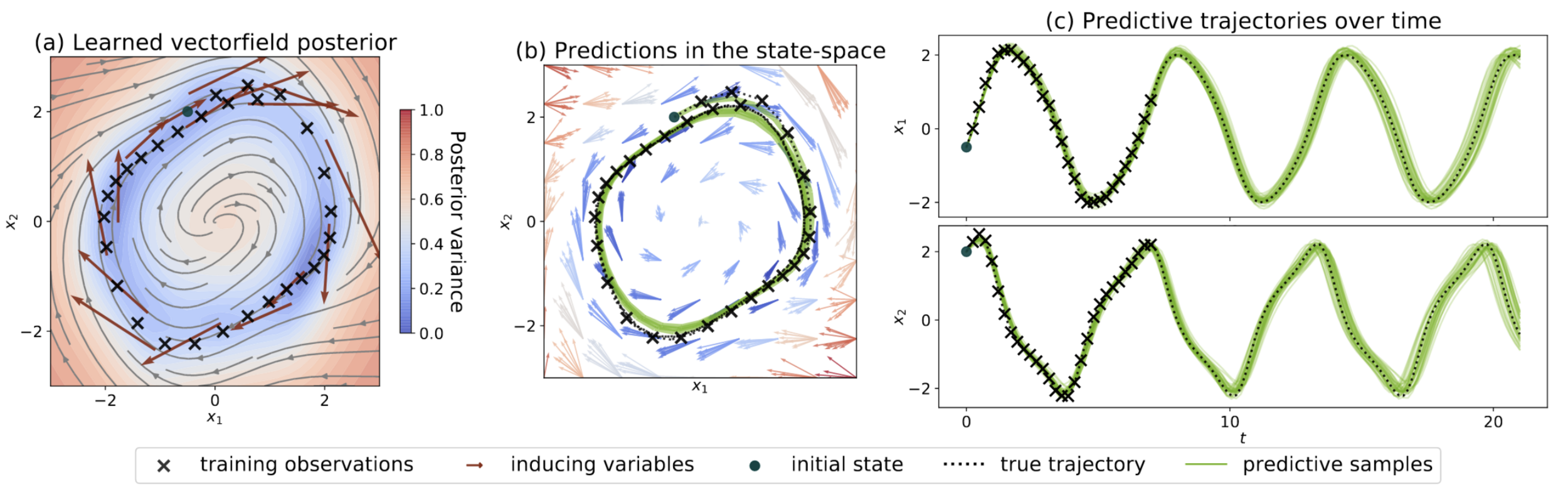
Fig. 4. Illustration of GPODE (Hegde et al., 2022)
Distribution of differentials
ODE state solutions are deterministic
\mathbf{x}_{i} =\mathbf{x}_{0} + \int_{0}^{t_{i}} \mathbf{f}(\mathbf{x}(\tau))d\tau \\
efficiently sample GP functions
\mathbf{f}(\cdot)\sim q(\mathbf{f})
efficiently sample GP functions
\mathbf{f}(\cdot)\sim q(\mathbf{f})
solution
Decoupled Sampling (Wilson et al., 2020)
\underbrace{f(\mathbf{x}) | \mathbf{u}}_\text{posterior} \approx \underbrace{\sum_{i=1}^{F} w_{i} \phi_{i}(\mathbf{x})}_\text{prior} + \underbrace{\sum_{j=1}^{M} \nu_{j}K(\mathbf{x},\mathbf{z}_{j})}_\text{update},
feature maps
Take away:
\phi(\mathbf{x})
by fixing random samples from
and
w
we can sample a unique (deterministic) ODE from
q(\mathbf{f})
feature maps
\phi(\mathbf{x})
an approximation of the kernel
What is our kernel?
The differential function
defines a vector field
\mathbf{f}(\cdot)
Which results in an Operator-Valued Kernel (OVK) (Alvarez et al. 2012)
\mathbf{K}_{\theta} = (K(\mathbf{x}_{i},\mathbf{x}_{j}))^{M}_{i,j=1} \in \mathbb{R}^{MD \times MD}
What is our approximation?
Random Fourier Features for OVK (Brault et al., 2016)
\tilde{\Phi}(x) = \frac{1}{\sqrt{F}}\bigoplus_{j=1}^{F} \binom{\textup{cos} \left \langle x, \omega_{j} \right \rangle B(\omega_{j})^{*}}{\textup{sin} \left \langle x, \omega_{j} \right \rangle B(\omega_{j})^{*}}
k(\mathbf{x_{i}},\mathbf{x_{j}})
- model nonparametric ODE with GP
- efficiently sample from GP posterior
- approximate OVK with RFF
. . . latent ODE with uncertainty and informative priors
Discussed so far. . .
. . . latent ODE with uncertainty and informative priors
VAE-GP-ODE
a probabilistic dynamical model with informative priors
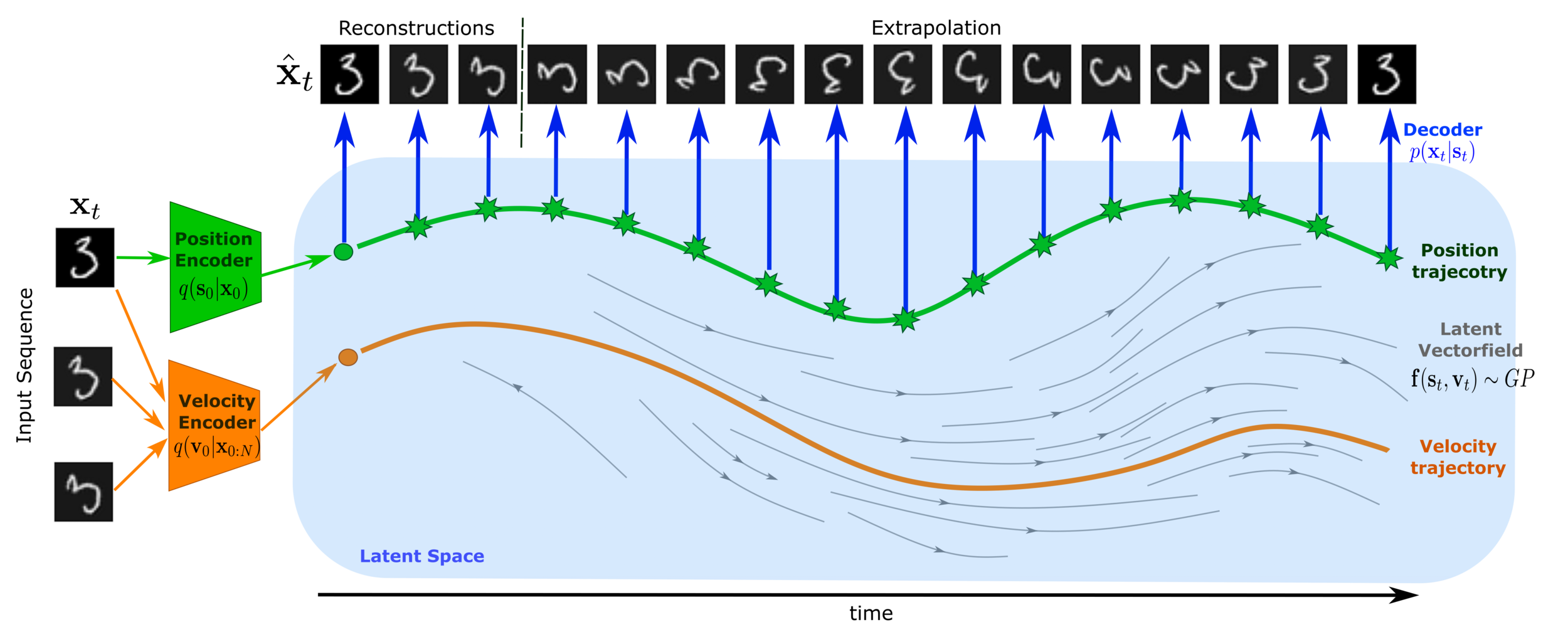
Fig. 5. Illustration of VAE-GP-ODE (Auzina et al., 2022)
Model architecture
Informative prior
Divergence Free Kernel
B(\omega) = I ||\omega|| - \frac{\omega \omega^{T}}{||\omega||_{2}},
\omega \sim N(\mathbf{0}, \mathbf{\Lambda}^{-1}),
\mathbf{\Lambda} = \text{diag}(l_{1}^{2}, l_{2}^{2}, \dots,l_{D}^{2})
\ddot{\mathbf{z}}_{t}:= \frac{d^{2}\mathbf{z}_{t}}{dt^2}=\mathbf{f}(\mathbf{z}_{t},\dot{\mathbf{z}}_{t})
\begin{matrix}
\left\{\begin{matrix}
\dot{\mathbf{s}}_{t}=\mathbf{v}_{t} \\
\dot{\mathbf{v}}_{t}=\mathbf{f}(\mathbf{s}_{t},\mathbf{v}_{t})
\end{matrix}\right. &
\begin{bmatrix}
\mathbf{s}_{T}\\
\mathbf{v}_{T}
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{s}_{0}\\
\mathbf{v}_{0}
\end{bmatrix}
+
\int_{0}^{T} \begin{bmatrix}
\mathbf{v}_{t}\\
\mathbf{f}(\mathbf{s}_{t},\mathbf{v}_{t})
\end{bmatrix}
dt
\end{matrix}
VAE-GP-ODE
Fig. 6. Reconstructed test sequences (Auzina et al., 2022)
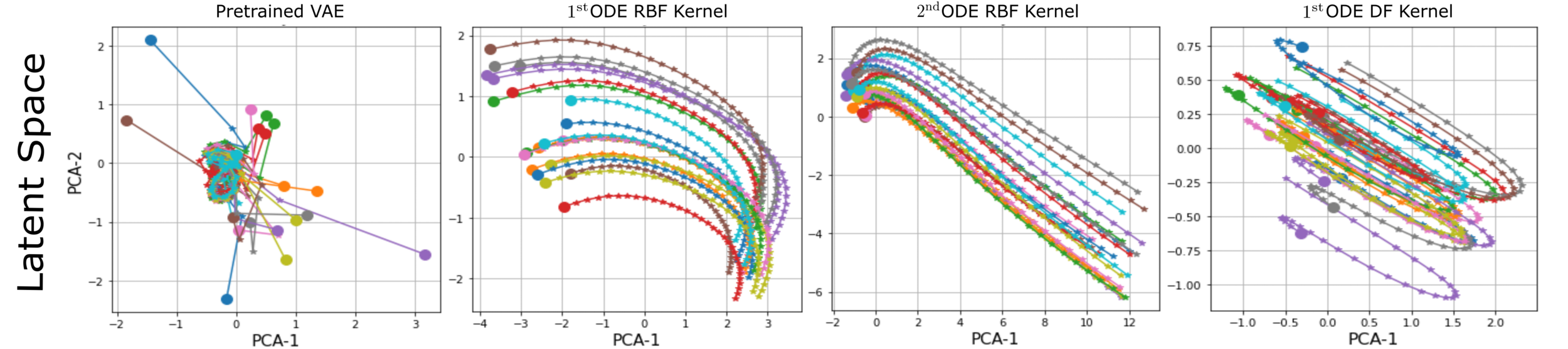
Fig. 7. Learned latent space (Auzina et al., 2022)
Possible Future Directions
Geometric Kernels (V. Borovistkiy et al. 2023)
Fig. 8. Samples from a GP with heat kernel covariance on the torus, real projective plane and on a sphere
GP with Helmholtz decomposition (R. Berlinghieri et al., 2022)
\underbrace{F}_{\text{Ocean Flow}} = \underbrace{\triangledown \Phi}_{\text{divergence}} + \underbrace{\triangledown \times \Psi}_{\text{vorticity}}
Fig. 9. Predicted abrupt current change
Thank you for your attention
Thank you for your attention
References
Get in touch
i.a.auzina@uva.nl
@AmandaIlze
Check out our work
Auzina, Ilze A., Yıldız, Çağatay, and Gavves, Efstratios. (2022). Latent GP-ODEs with Informative Priors. 36th NeurIPS Workshop on Causal Dynamics
https://github.com/IlzeAmandaA/VAE-GP-ODE
Auzina, I. A., Yıldız, Ç., Magliacane, S., Bethge, M., and Gavves, E. (2023). Invariant Neural Ordinary Differential Equations. arXiv preprint arXiv:2302.13262
TBA
Alvarez, M. A., Rosasco, L., & Lawrence, N. D. (2012). Kernels for vector-valued functions: A review. Foundations and Trends® in Machine Learning, 4(3), 195-266.
Azangulov, I., Smolensky, A., Terenin, A., & Borovitskiy, V. (2022). Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces I: the Compact Case. arXiv preprint arXiv:2208.14960.
Berlinghieri, R., Trippe, B. L., Burt, D. R., Giordano, R., Srinivasan, K., Özgökmen, T., ... & Broderick, T. (2023). Gaussian processes at the Helm (holtz): A more fluid model for ocean currents. arXiv preprint arXiv:2302.10364.
Brault, R., Heinonen, M., & Buc, F. (2016, November). Random fourier features for operator-valued kernels. In Asian Conference on Machine Learning (pp. 110-125). PMLR.
Chen, R. T., Rubanova, Y., Bettencourt, J., & Duvenaud, D. K. (2018). Neural ordinary differential equations. Advances in neural information processing systems, 31.
Hegde, P., Yıldız, Ç., Lähdesmäki, H., Kaski, S., & Heinonen, M. (2022, August). Variational multiple shooting for Bayesian ODEs with Gaussian processes. In Uncertainty in Artificial Intelligence (pp. 790-799). PMLR.
Wilson, J., Borovitskiy, V., Terenin, A., Mostowsky, P., & Deisenroth, M. (2020, November). Efficiently sampling functions from Gaussian process posteriors. In International Conference on Machine Learning (pp. 10292-10302). PMLR.
SIAM 2023
By iaa
