Invariant NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
Invariant NODEs
Key Idea:
length, mass
length of limbs
influence dynamics
influence reconstruction
color of a ball
color of clothes
does setting apart dynamic states from
underlying static factors of variation improve existing model performance?
Invariant NODEs
Key Idea:
does setting apart dynamic states from
underlying static factors of variation improve existing model performance?
influence dynamics
influence reconstruction
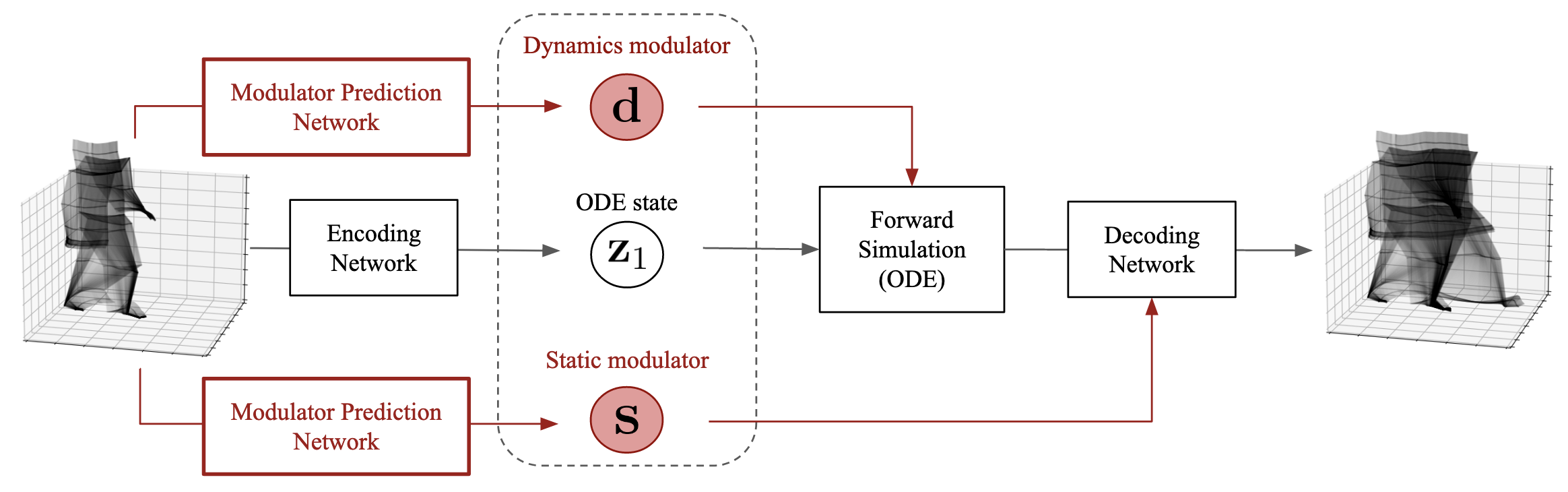
Figure 1. Schematic illustration of our method.
Invariant NODEs
Figure 1. Schematic illustration of our method.
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
d∼p(d) // dynamics modulator
\mathbf{d} \sim p(\mathbf{d}) ~\quad \textit{// dynamics modulator} \\
s∼p(s) // static modulator
\mathbf{s} \sim p(\mathbf{s}) ~~\quad \textit{// static modulator} \\
z1∼p(z1)// latent ODE state
\mathbf{z}_1 \sim p(\mathbf{z}_1) \quad \textit{// latent ODE state} \\
I. Generative Model
xi∼pxi(xi∣zi ; s).
\mathbf{x}_i \sim p_{\mathbf{x}_i}(\mathbf{x}_i \mid \mathbf{z}_i ~;~ \mathbf{s}).
zi=z1+∫t1tifθ(z(τ);d) dτ
\mathbf{z}_i = \mathbf{z}_1 + \int_{t_1}^{t_i} \mathbf{f}_{\mathbf{\theta}}(\mathbf{z}(\tau);\mathbf{d})~d \tau \\
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
d∼p(d) // dynamics modulator
\mathbf{d} \sim p(\mathbf{d}) ~\quad \textit{// dynamics modulator} \\
s∼p(s) // static modulator
\mathbf{s} \sim p(\mathbf{s}) ~~\quad \textit{// static modulator} \\
II. Learning Latent Modulator variables
(i) static modulator
sn=T1∑i=1Tsin,sin=gψ(xin).
\mathbf{s}^{n} = \frac{1}{T} \sum_{i=1}^{T} \mathbf{s}^{n}_i, \qquad \mathbf{s}^{n}_i = \mathbf{g}_\psi\big(\mathbf{x}^{n}_i\big).
// compute average over the observation embedings
time-invariance
// concatenate with latent ODE state
xin∼pxi(xin[zin,sn]) ∀i∈[1,…,T].
\mathbf{x}^{n}_i \sim p_{\mathbf{x}_i}\Big(\mathbf{x}^{n}_i \Big\vert \big[\mathbf{z}^{n}_i,\mathbf{s}^{n}\big]\Big) ~~ \forall i \in [1,\ldots,T].
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
d∼p(d) // dynamics modulator
\mathbf{d} \sim p(\mathbf{d}) ~\quad \textit{// dynamics modulator} \\
s∼p(s) // static modulator
\mathbf{s} \sim p(\mathbf{s}) ~~\quad \textit{// static modulator} \\
II. Learning Latent Modulator variables
(i) dynamics modulator
dn=T−Te1∑i=1T−Tedin,din=hυ(xi:i+Ten),
\mathbf{d}^{n} = \frac{1}{T-T_e} \sum_{i=1}^{T-T_e} \mathbf{d}^{n}_i, \qquad \mathbf{d}^{n}_i = \mathbf{h}_{\upsilon}\big(\mathbf{x}^{n}_{i:i+T_e}\big),
// compute over subsequences of length
time-invariance
// pass as input to the differential function
dtdzn(t)=fθ(zn(t),dn)
\frac{\textrm{d}\mathbf{z}^{n}(t)}{\textrm{d}t} = \mathbf{f}_\mathbf{\theta} \big(\mathbf{z}^{n}(t), \mathbf{d}^{n} \big)
Te
T_e
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
A general framework
Latent NODE
(Chen et al., 2018)
Second Order NODE
(Norchliffe et al., 2020)
Latent Second Order NODE
(Yildiz et al., 2019)
Heavy Ball NODE
(Xia et al., 2021)
can be applied to most x-NODE
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
A general framework
that improves performance
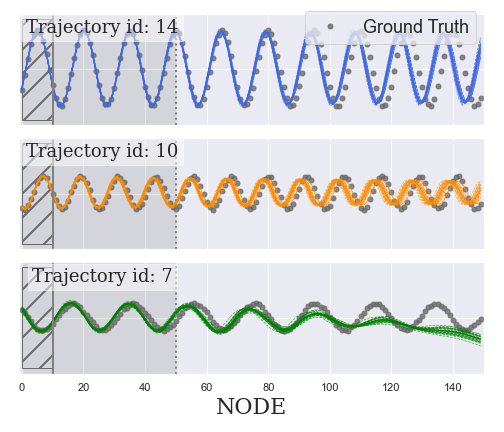
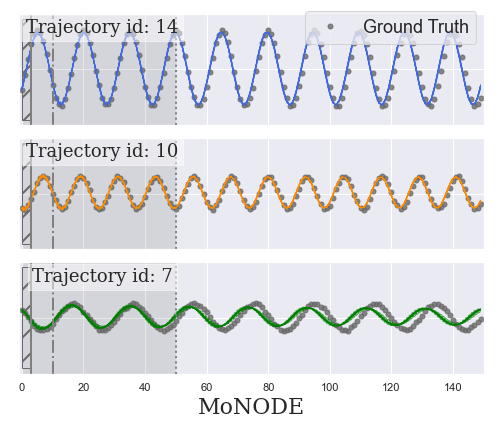
Sinusoidal Data
Latent NODE
(Chen et al., 2018)
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
A general framework
that improves performance
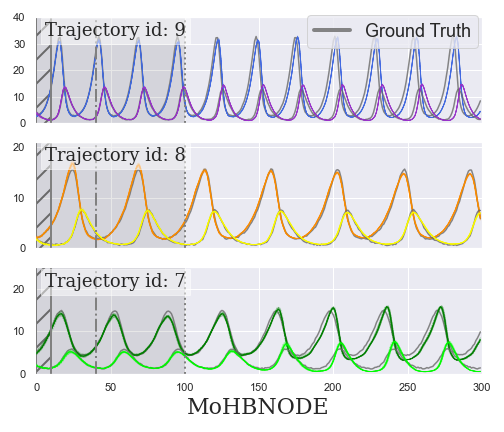
Predator-Prey (PP) data
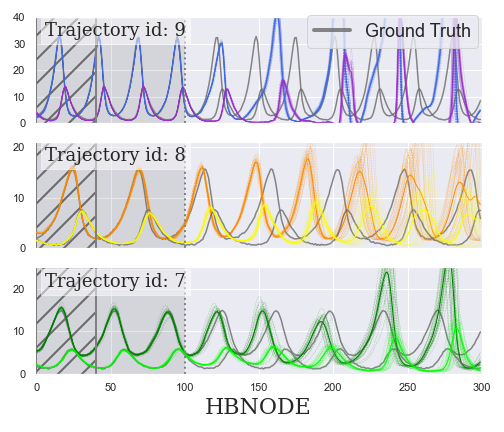
Heavy Ball NODE
(Xia et al., 2021)
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
that improves performance
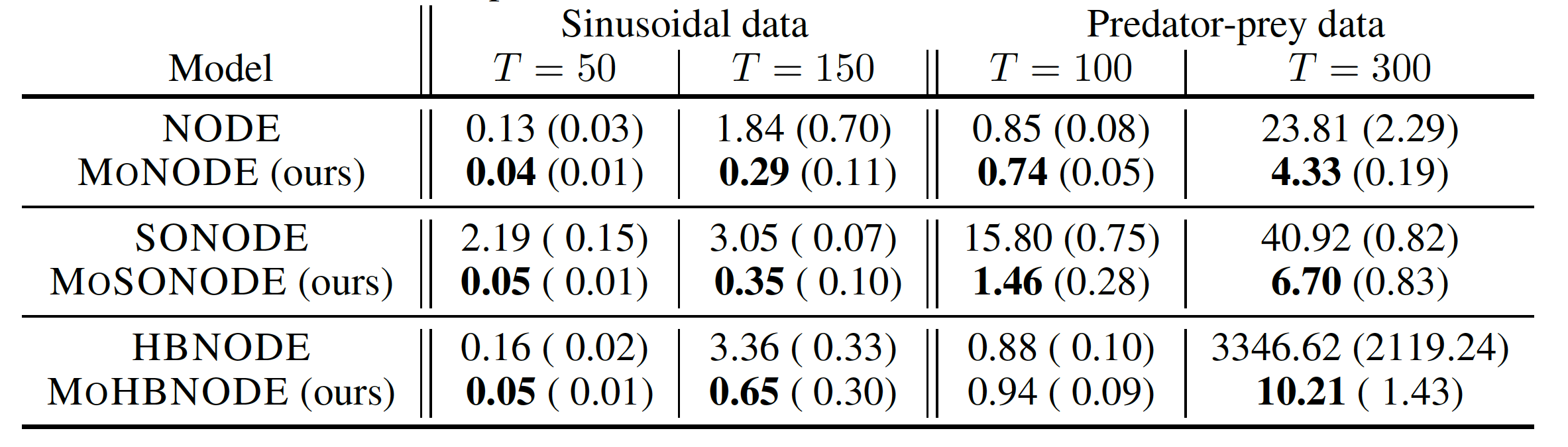
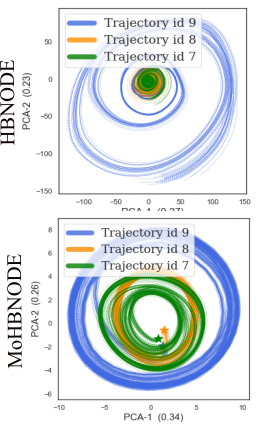
with respect to forecasting and generalization
with respect to disentanglement
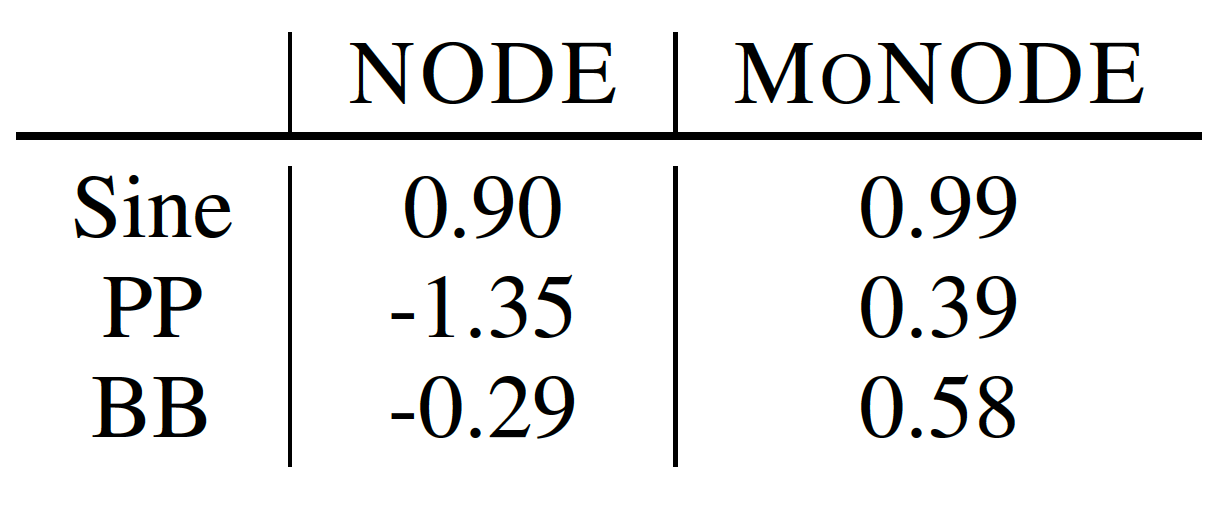
Table 1. Test MSE and its standard deviation with and without our framework. Lower is better.
Table 2. R^2 scroes to predict the unknown Factors of Variation from inferred latents. Higher is better.
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
that improves performance
on real world data
Table 3. Test MSE and standard deviation. Lower is better.
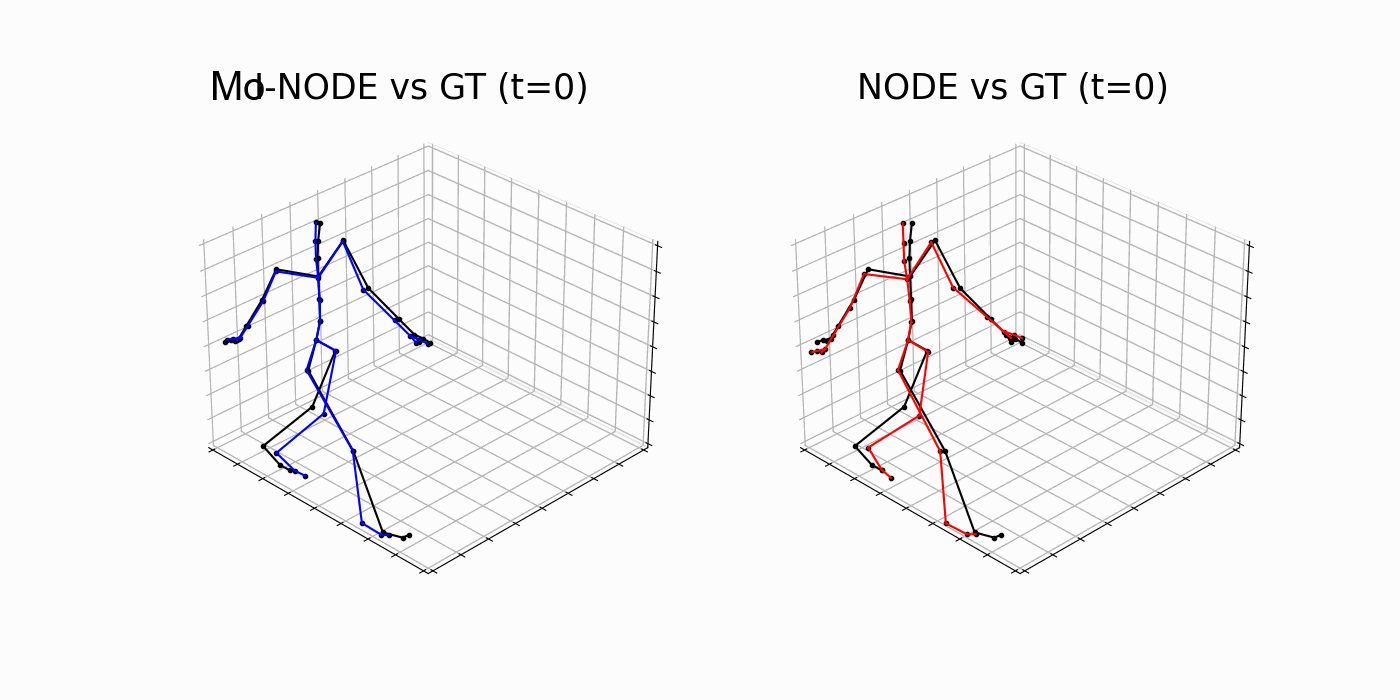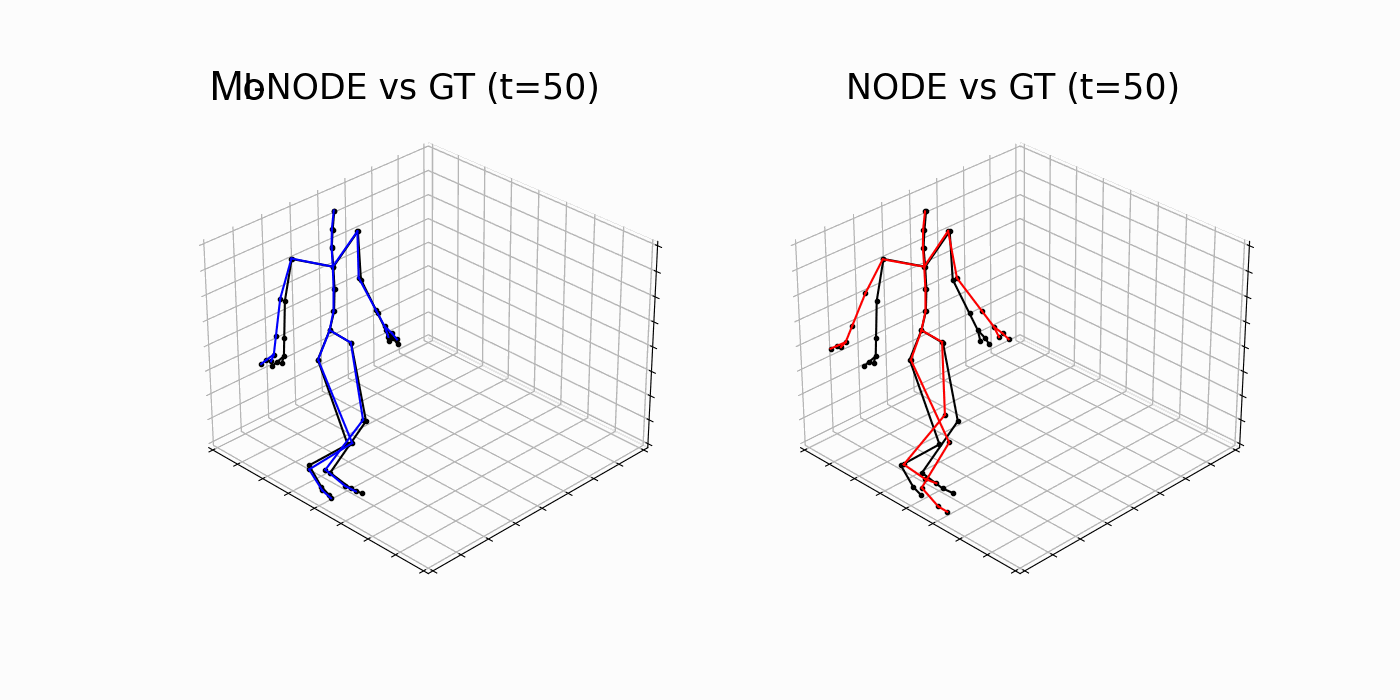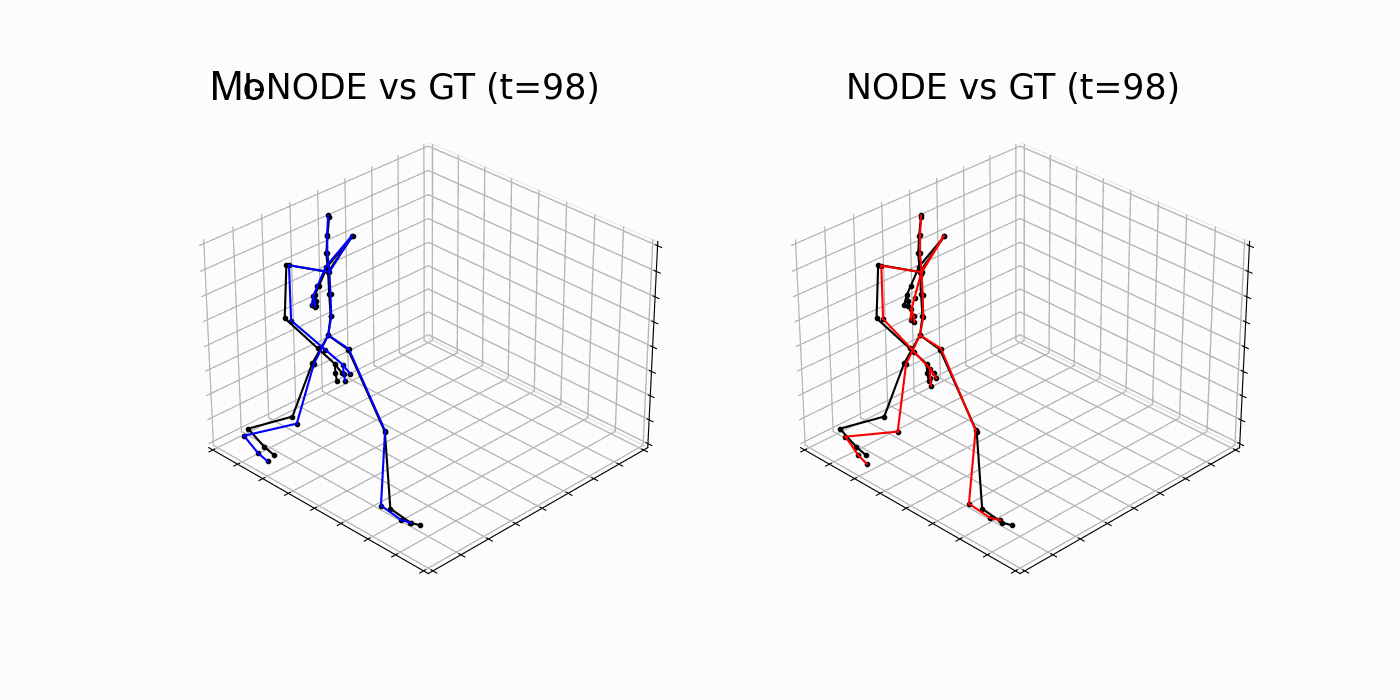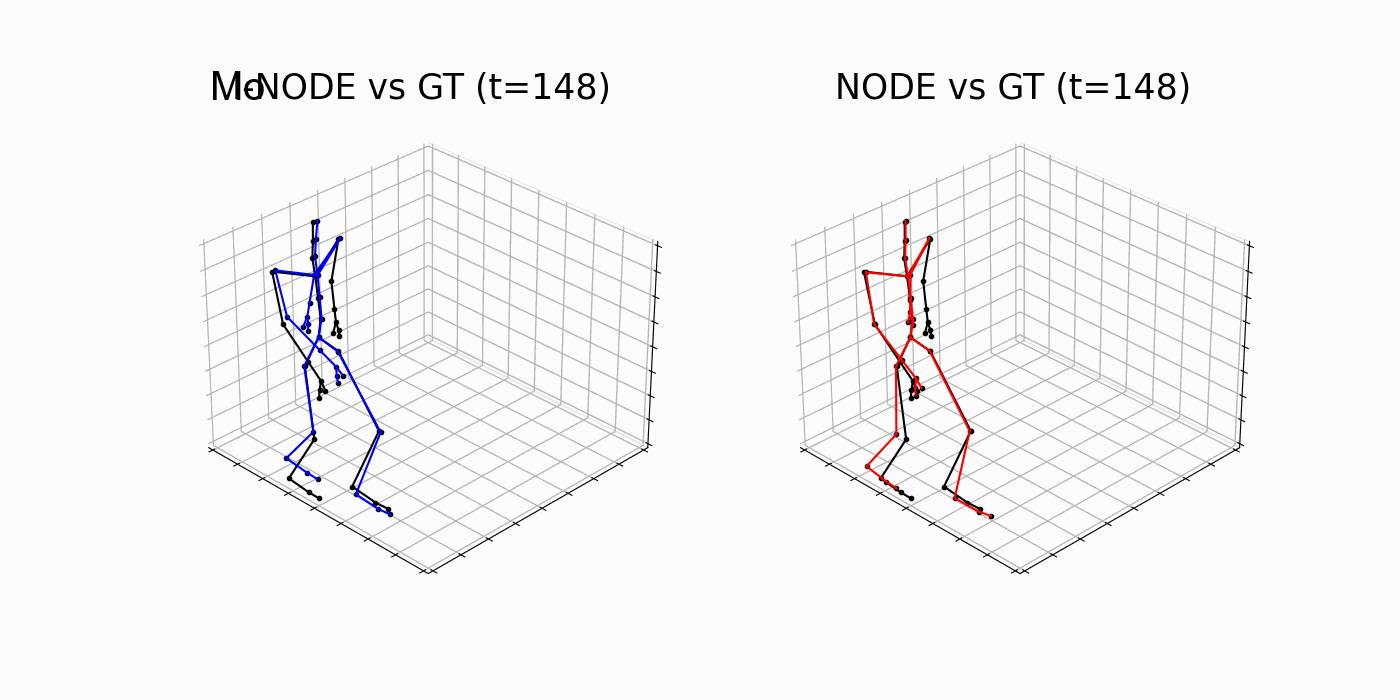
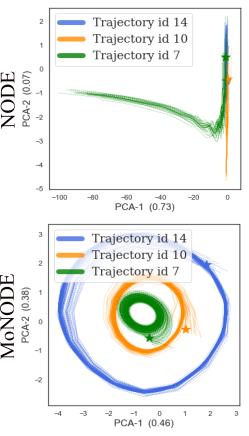
MoNODE
NODE
Modulated NODEs
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
We introduce a modulator framework for NODE models that allows to separate time-evolving ODE states from modulator variables
Limitations/Extensions
- express constants as modulator variables
Benefits
- improved generalization
- improved far-horizon forecasting
- capture true known FoV
- limited to deterministic systems
- out of distribution modulators
- self-supervised contrastive loss
- interpretability /disentanglement
Modulated ....
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
Biology Applications
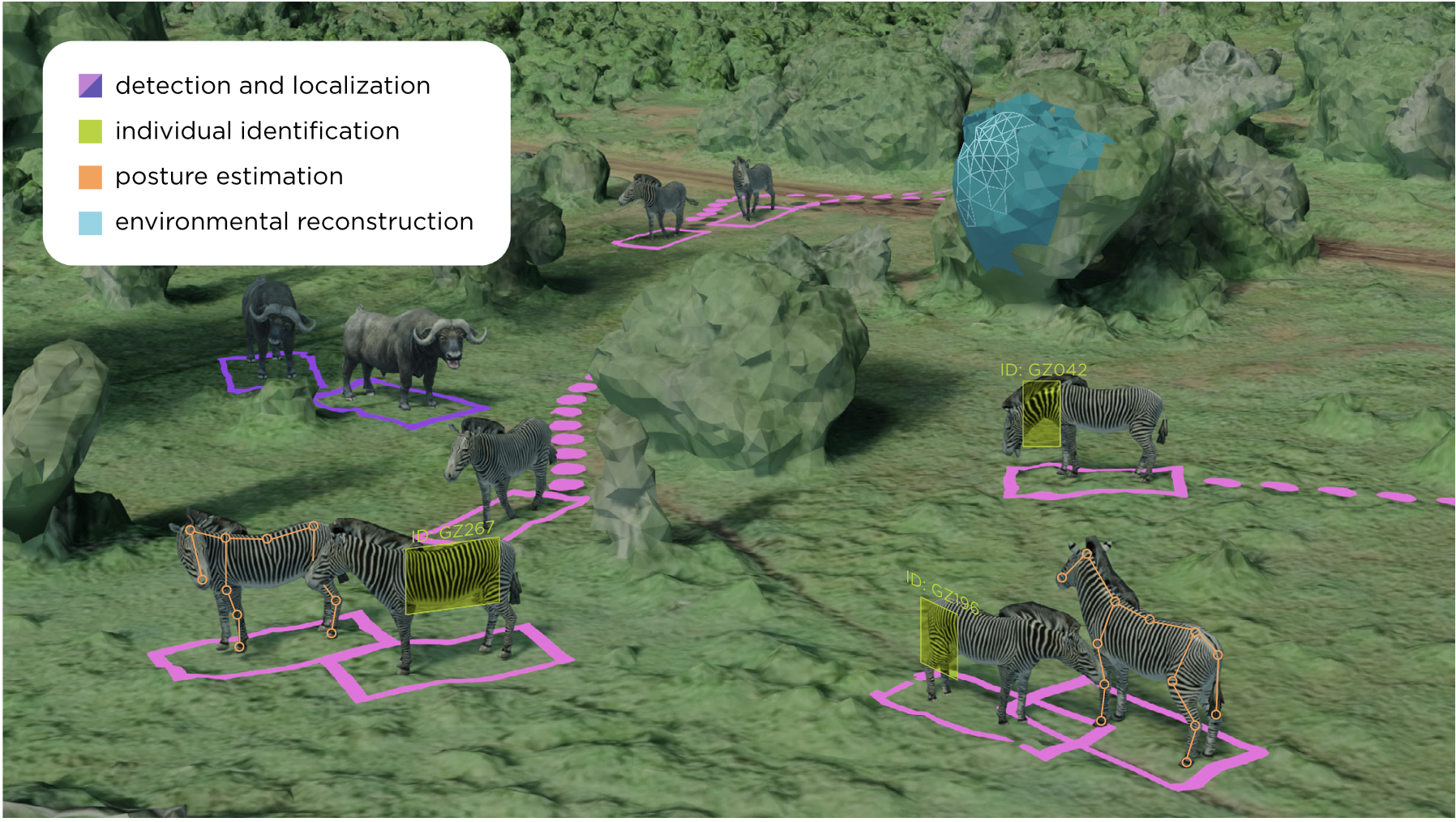
Object-centric representations
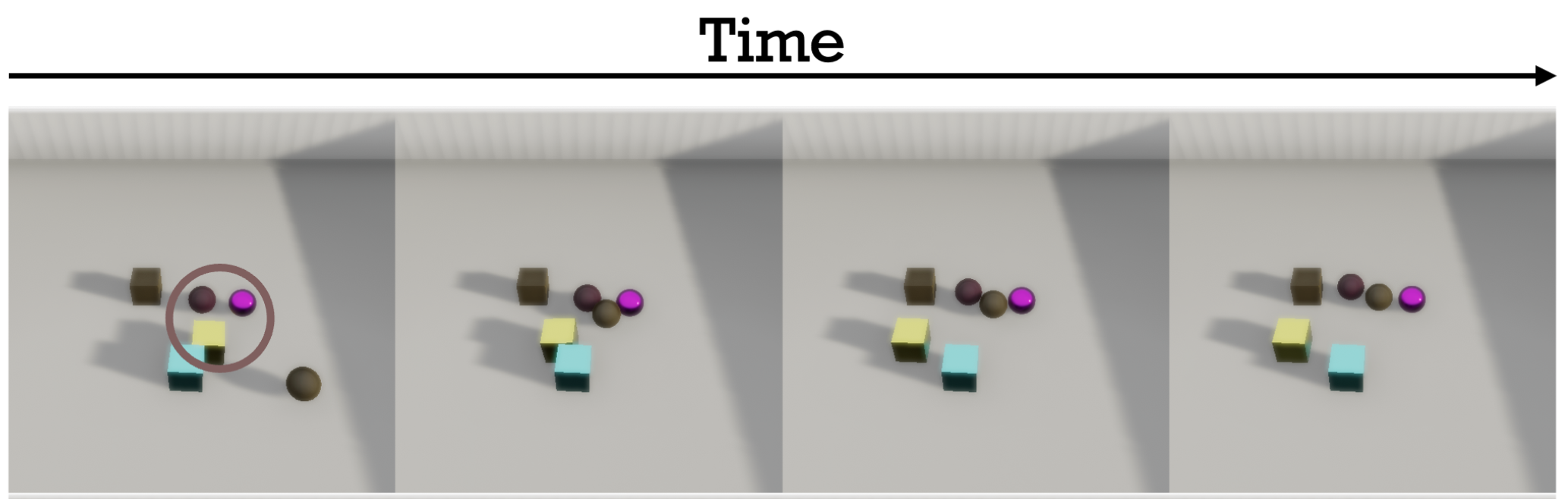
Thank you for your attention
I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
Modulated NODEs
Invariant NODEs I.A. Auzina, C. Yıldız, S. Magliacane, M. Bethge and E. Gavves
Modulated NODEs Boston University 2023
By iaa
Modulated NODEs Boston University 2023
- 304
