Forgalom igény tudatos hálózat tervezés
Készítette:
Szecsődi Imre
Programtervező informatikus
MSc


Budapest, 2020
Témavezető:
Dr. Lukovszki Tamás
Egyetemi docens, PhD
Megjegyzés
- A diplomamunka a C. Avin, K. Mondal, and S. Schmid. Demand-aware network design with minimal
congestion and route lengths cikket vette alapjául.
Motiváció
- A technika előrehaladásával egyre nagyobb lett a feldolgozandó adatok mennyisége
- Adattárházakban a szerverek közötti kommunikáció is megnövekedett ezáltal
- A jelenlegi hálózatok a legrosszabb esetre vannak tervezve, azaz, hogy majdnem teljes sávszélességű, kétirányú kapcsolat álljon fent bármelyik két szerver között
- A valós kommunikáció nem ezt a sémát követi, hanem túlnyomó részt megadott párok között történik a legtöbb kommunikáció
Valós forgalmi adatok
- Microsoft Research ProjecToR adatai, Microsoft adattárházában 250 ezer szervert 5 production klaszterben elosztva





Hálózat tervezési stratégiák
- A technika fejlődésével elérhetővé váltak eszközök arra, hogy egy adott hálózatot újra konfiguráljunk, attól függően milyen terhelés éri
- pl, korábbi kommunikációs minták alapján
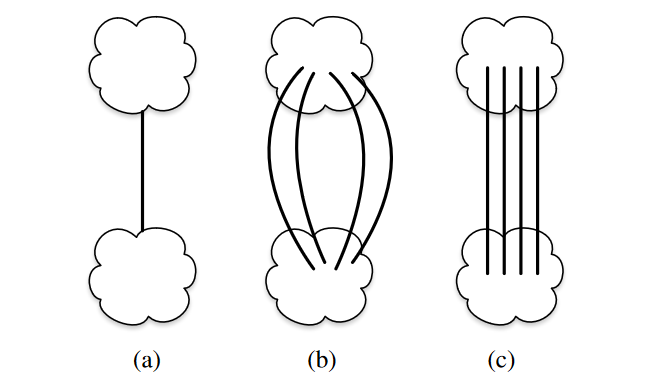
- Két fő optimalizációs lehetőség van, legyen rövid az út (a) vagy legyen minimális a torlódás (b)
- A cikk bemutat egy módszert arra, hogy lehet mindkettőre majdnem optimális megoldást adni egyszerre (c)
Hálózat tervezési stratégiák
Újra konfigurálás megvalósítása
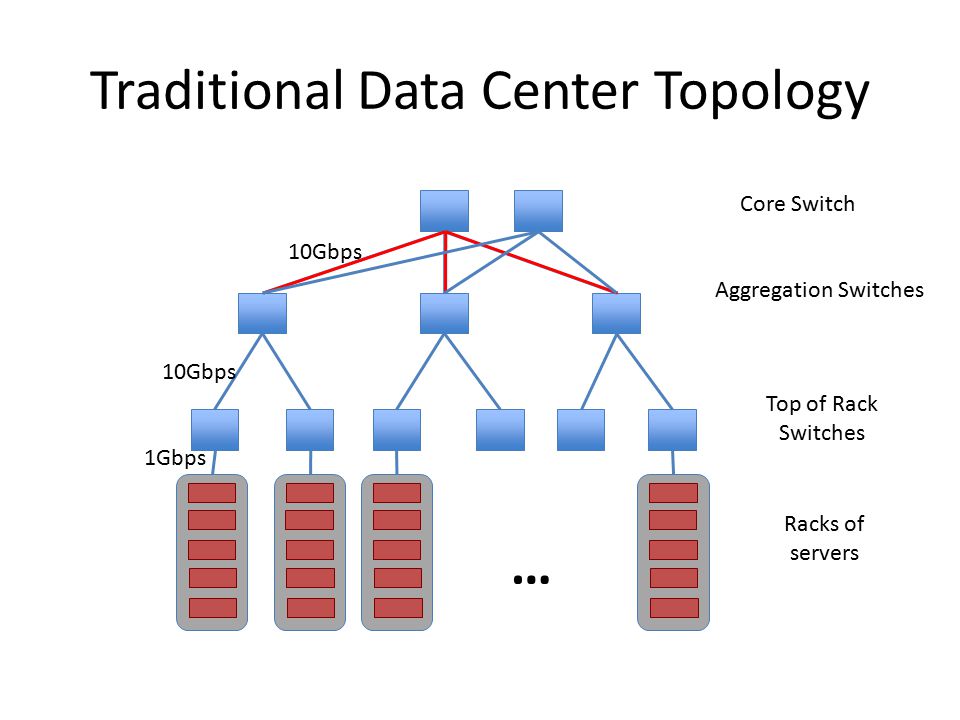
- Átlag hálózatok statikusan vannak konfigurálva, nem sok lehetőséget adva annak, hogy változtassunk
- pl. Ethernet switch

Újra konfigurálás megvalósítása
- Optikai switchek már újra tudják konfigurálni magukat, de ezek "lassúak"
Újra konfigurálás megvalósítása
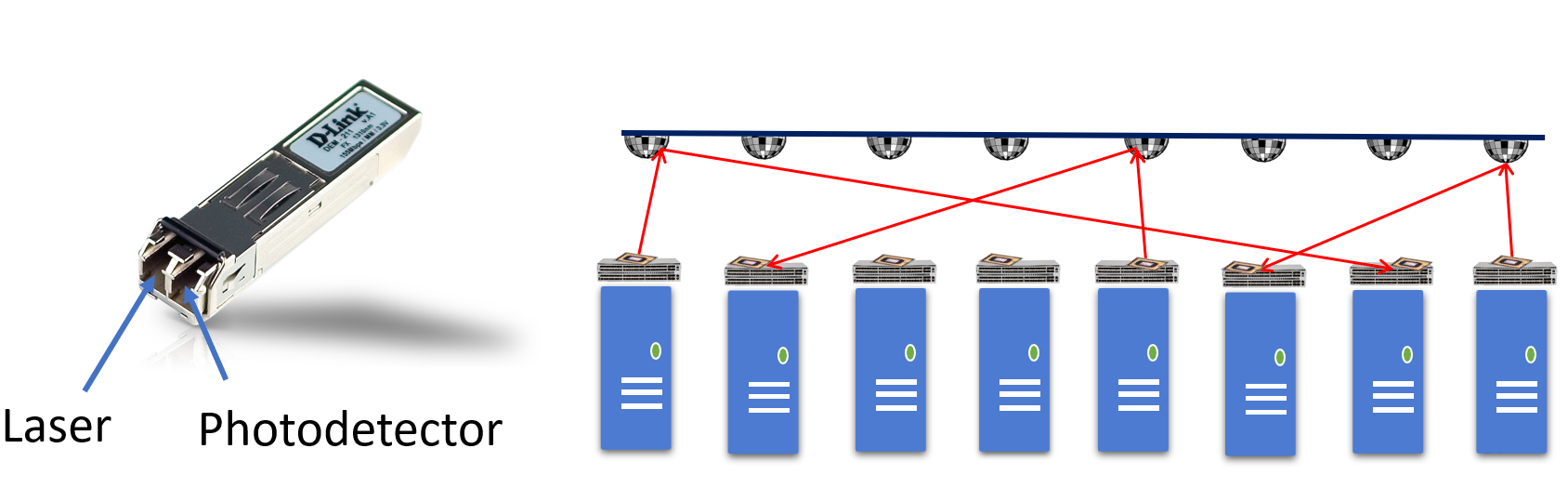
- Microsoft Research - ProjecToR, lézer segítségével kiváltani az optikai swticheket
- 12 µs váltás idő ( 2500x gyorsabb mint egy optikai hálózati switch)
Forgalom igény tudatos hálózat tervezés probléma
- Vegyünk egy hálózatot meghatározott számú csomóponttal
- A hálózathoz tartozik egy demand mátrix, ami leírja a valószínűségét annak, hogy \(i\) forrásból mekkora eséllyel lesz adat küldve \(j\) célba
- A cél, hogy ezen adatból egy olyan hálózati séma készítése, ami kis torlódást és rövid utakat eredményez, ez mellett még skálázható is
Példa
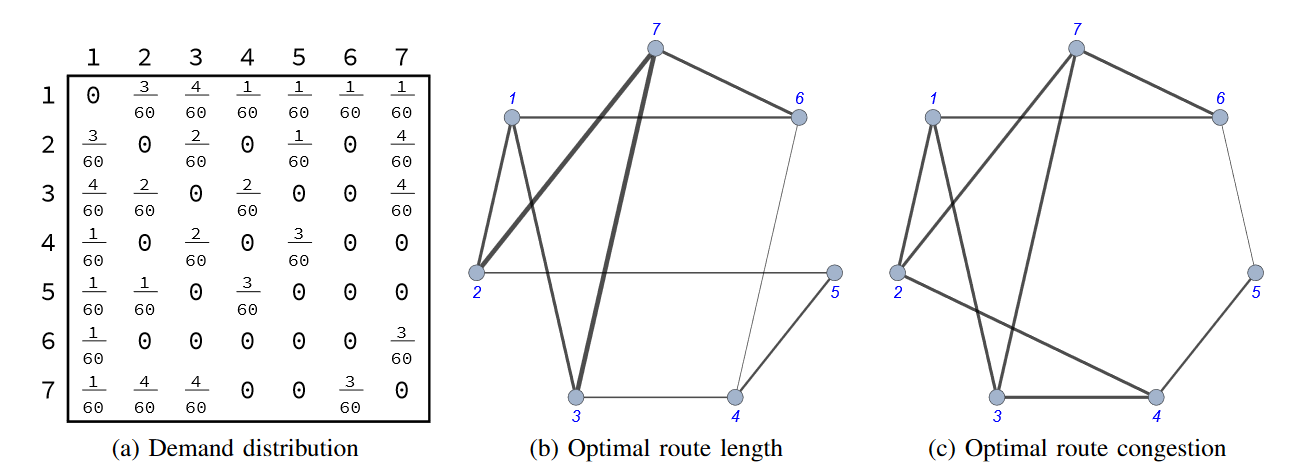
Formális felírás
- Adott N darab csúcspont V = {1, ..., N}, és egy kommunikációs séma \( M_D \), ami egy N×N mátrix
- A mátrix \((i, j)\) eleméhez tartozik egy \(p(i, j)\) valószínűség, ahol \(i\) a forrás csomópont és \(j\) a cél.
- A bemeneti mátrix ábrázolható egy irányított \(G_D\) gráfban, ahol az élsúlyok a két pont közötti kommunikációs valószínűség
- Az algoritmus feltétele, hogy a mátrix ritka legyen
Formális felírás
- Egy N hálózatra a torlódást és az úthosszt útválasztási sémával fogjuk definiálni
- Egy útválasztási séma az N hálózatra \(\Gamma(N)\), ami a \(\Gamma_{uv}\) utak halmaza, ahol \((u, v)\) párok különböző utakat jelölnek
- \(\Gamma_{uv}\) egy útsorozat, ami összeköti \(u\) pontot \(v\) ponttal
Torlódás
- (Definíció 1) A torlódást egy \(\Gamma(N)\) útválasztási sémán a \(D\) demand mátrix segítségével írjuk fel: \[C(D, \Gamma(N)) = \max_{e \in \Gamma(N)} \sum_{e \in \Gamma(uv)} p(u,v) \]
Úthossz
- (Definíció 2) Az átlag súlyozott úthosszt egy \(\Gamma(N)\) útválasztási sémán a \(D\) demand mátrix segítségével írjuk fel: \[L(D, \Gamma(N)) = \sum_{(u,v) \in D} p(u,v) \cdot d_{\Gamma(N)}(u, v) \] ahol a \(d_{\Gamma(N)}(u, v)\) az útvonal hosszát jelöli
Skálázhatóság
- A hálózatot skálázhatóra kell tervezni, ezért meghatározunk egy \(\Delta\) konstans fokszámot, ami a maximális csatlakozások számát fogja meghatározni egy adott csomóponthoz
- \(N_\Delta\) jelölje az összes \(\Delta\) fokszámú gráfot, és elváruk, hogy \(N \in N_\Delta\)
Optimális torlódás és úthossz
- Az optimális torlódást egy hálózatra, úgy határozzuk meg, hogy a csak a torlódást vesszük figyelembe számításkor \[C^*(D, \Delta) = \min_{N \in N_\Delta, \Gamma(N)} C(D, \Gamma(N))\]
- Az optimális úthosszt egy hálózatra, úgy határozzuk meg, hogy a csak az úthosszt vesszük figyelembe számításkor \[L^*(D, \Delta) = \min_{N \in N_\Delta, \Gamma(N)} L(D, \Gamma(N))\]
cl-DAN hálózat tervezése
- (Definíció 3) Adott egy \(D\) demand mátrix, és egy \(\Delta\) maximális fokszám, az \((\alpha, \beta)\)-cl-DAN hálózat tervezési probléma:
- Hogy tervezzünk egy olyan \(N \in N_\Delta\) hálózatot, és egy hozzá tartozó \(\Gamma(N)\) útválasztási sémát, ami közel optimális torlódásra és úthosszra is
- Az algoritmus egy felső korlátot tud adni arra, hogy mennyivel fog eltérni a megoldás az optimálistól
- Torlódásra: \[C(D, \Gamma(N)) \le \alpha \cdot C^*(D, \Delta) + \alpha'\]
- Úthosszra: \[L(D, \Gamma(N)) \le \beta \cdot L^*(D, \Delta) + \beta'\]
EgoTree - EgoFák
- Az Egofa egy torlódásra és úthosszra optimalizált fa hálózat egy csomópontra nézve
- Az Egotree-t definiáljuk a következő módon, \[EgoTree(s, \bar{p}, \Delta) \]
- \(s\) a forrás csomópont
- \(\bar{p}\) a szomszédainak eloszlásai
- \(\Delta\) fokszám
- Ez közel optimális megoldást ad torlódásra és úthosszra
1. Tétel
- Adott egy \(\bar{p}\) frekvencia eloszlás az \(s\) forrás ponthoz, és adott egy \(\Delta\) fokszám, ekkor az \(EgoTree(s, \bar{p}, \Delta)\) egy \((\alpha, \beta)\)-cl-DAN a következő paraméterekkel:
- \(\alpha = \frac{4}{3}\)
- \(\beta = log^2(\Delta + 1)\)
\(EgoTree(s, \bar{p}, \Delta)\) algoritmus
- \(s\) a gyökér elem, \(\Delta\) fokszámmal, üres fa
- Rendezzük sorba \(\bar{p} = \{p1, p2, ..., p_k\}\) valószínűségeket csökkenő sorrendben
- Kezdjük rárakni a fára a csomópontokat, a gyökér elemre legfeljebb \(\Delta\) levél kerülhet
- Mikor elértük a \(\Delta\) levelet, a következő csomópontokat mindig a legkisebb összesített súlyú levélre kapcsolok rá, itt már legfeljebb két levele lehet minden fának
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}\)
s
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.1, .1, .1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.1, .1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
\(S_4 = .10\)
\(p_4(.10)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .20\)
\(S_4 = .10\)
\(p_4(.10)\)
\(p_5(.10)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .20\)
\(S_4 = .20\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .27\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .20\)
\(S_4 = .20\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .27\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .25\)
\(S_4 = .20\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .27\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .25\)
\(S_4 = .22\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{.01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .27\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .25\)
\(S_4 = .23\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
Példa
\(EgoTree(s, \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}, 4)\)
\( \{\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .27\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .25\)
\(S_4 = .24\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
Algoritmus elemzése
- A kapott eredményben látható, hogy a maximális torlódás a legnagyobb súlyú élen van
- Minimalizálni ezt, lényegében egy időzítés probléma, hogy osszuk ki a munkákat \(\Delta\) processzornak, hogy minden leghamarabb kész legyen
- Erre az optimális algoritmus NP-nehéz, de van közelítő módszer
Longest Processing Time (LPT)
- Először sorba rendezzük a feladatokat hossz szerint csökkenő sorrendben
- Ha van szabad processzor, akkor ahhoz rendeli a leghosszabb munkát
- Ha nincs akkor ahhoz a processzorhoz rendeli, ahol a legkevesebb ideig tart a munka
- (2. Tétel) Legyen \(\omega_L\) a maximum idő, mielőtt egy processzor befejezi az összes munkát a mohó LPT algoritmus szerint, és \(\omega_0\) az optimális, ekkor \[\frac{\omega_L}{\omega_0} \le \frac{4}{3} - \frac{1}{3\Delta}\]
- Ez az algoritmus polinom időben lefut
1. Tétel kiegészítése
- (1. Lemma) Az \(EgoTree(s, \bar{p}, \Delta)\) ad egy \(\frac{4}{3}\) szorzóval nagyobb közelítést a minimális torlódásra az optimális \(\Delta\) fokú fához képest, ami kiszolgál \(\bar{p}\) frekvencia eloszlást egy adott \(s\) forrás csomópontra
- (2. Lemma) Az \(EgoTree(s, \bar{p}, \Delta)\) ad egy \(log^2(\Delta + 1)\) szorzóval nagyobb közelítést a minimális úthosszra az optimális \(\Delta\) fokú fához képest, ami kiszolgál \(\bar{p}\) frekvencia eloszlást egy adott \(s\) forrás csomópontra
3. Tétel
- Legyen \(D\) egy szimmetrikus kommunikáció kéréseloszlás , ahol az átlag csúcs fokszáma \(\rho\), (azaz az élek száma \(\rho \cdot \frac{n}{2}\). Ekkor a maximum fokszám \(\Delta = 12\rho\), ehhez lehetséges generálni egy \((\alpha, \beta)\)-cl-DAN hálózatot, ahol
- \(\alpha = 1 + (\frac{8}{9})\Delta\)
- \(\beta = 1 + 4log^2(\Delta + 1)\)
- Konstans \(\rho\) esetén ez konstans közelítést ad a minimális torlódásra és az optimális úthosszra
\((\alpha, \beta)\)-cl-DAN algortimus
- Felosszuk a hálózat csúcsait két halmazra, \(H\) - magas és \(L\) - alacsony fokszámúakra fele-fele arányban
- Az alacsony fokszámú csúcsok fokszáma legfeljebb \(2\rho\)
- Megkeressük az összes olyan \((u, v)\) élt, ahol \(u\) és \(v\) is a magas fokszámú halmazba tartozik
- Az ilyen éleket a gráfban kiegészítjük egy segítő csomóponttal, \(l \in L\), az eredeti csomópontok között megszüntetjük az élt, és felveszünk két új élt \((u, l)\) és \((v, l)\)
- Minden segítő \(l\) csúcs választásakor egy még nem felhasználtat válasszunk az \(L\) halmazból
\((\alpha, \beta)\)-cl-DAN algortimus
- 4. Meghatározunk egy mátrixot, ami első lépésben az eredeti
- Ahol segítő csomópontot vettünk fel, ott az útvonal hosszúhoz hozzá kell még adni az \(l\)-el való áthaladást is, és törölni kell az eredeti pontok közti élt
- Ezután elkészítjük a magas halmaz csúcsaira a \(T_u\) fát, ahol a valószínűségeket a mátrixból kiolvassuk, \(\Delta = 12\rho\) fokszámmal, ez közel optimális megoldást ad mindkét fel
\((\alpha, \beta)\)-cl-DAN algortimus
- 5. Mivel \(u\) és \(v\) pontok közt egy \(l\) segítő csomópont van használva ezért \(T_u\) és \(T_v\) módosításra szorul. Alakítsuk át először \(T_u\)-t \(T'_u\)-ra
- Ha \(l \notin T_u\), \((p(u, l) = 0)\), akkor \(l\) átveszi \(v\) helyét \(T'_u\)-ban
-
Ha \(l \in T_u\), \((p(u, l) \gt 0)\), akkor két lehetőségünk van:
- Ha \((p(u, l) \gt (p(u, v))\), akkor töröljük \(v\)-t a fából
- Ha \((p(u, l) \le (p(u, v))\), akkor \(l\) átveszi \(v\) helyét \(T'_u\)-ban
- \(T'_v\) hasonlóan számítjuk ki, ezzel garantálva, hogy \(T'_u\) és \(T'_v\) közötti kommunikáció az \(l\) csomóponton keresztül fog áthaladni
5. lépés vizualizálása
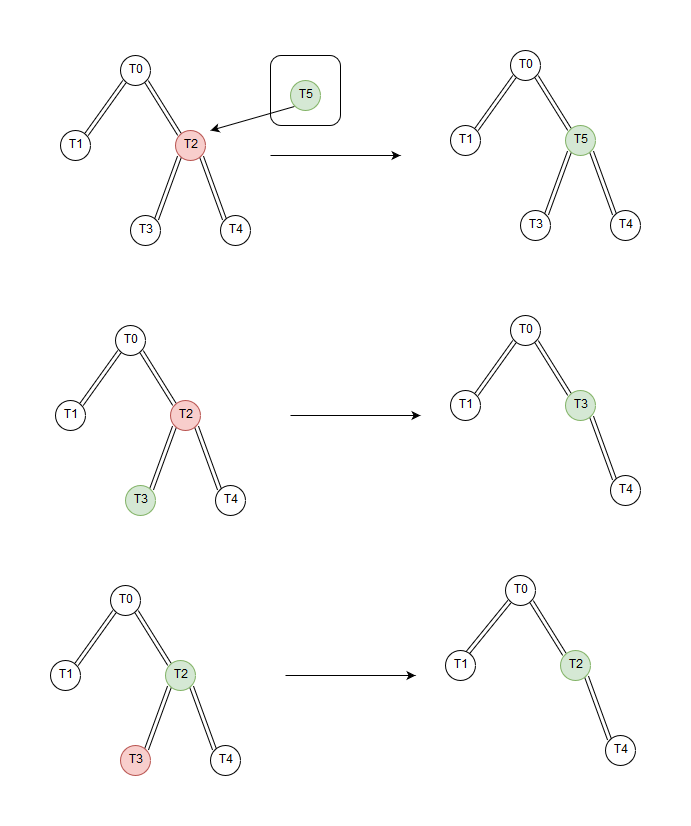
\((\alpha, \beta)\)-cl-DAN algortimus
- 6. Konstruáljuk meg az új N hálózatot, vegyük az előbb készített egofákat és vegyük az uniójukat, azaz húzzuk be az összes olyan élet amik szerepeltek a fákban
- De mivel nem csak magas fokú csomópontok közt történhetett adatforgalom, ezért még vegyük hozzá az N hálózathoz azokat az éleket is, ahol mindkét csomópont alacsony fokszámú volt
\((\alpha, \beta)\)-cl-DAN algortimus példa
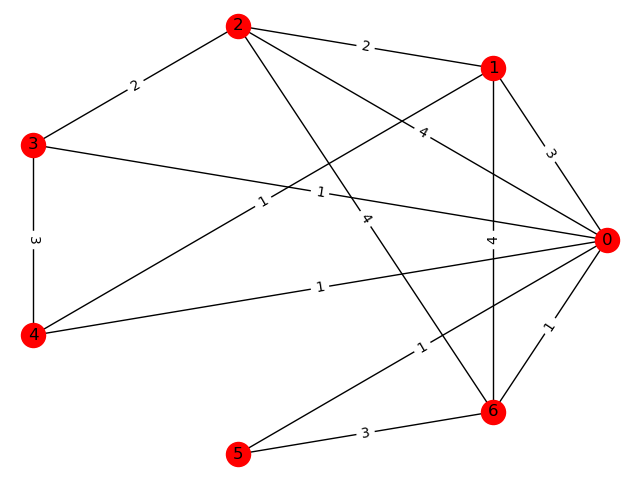
\((\alpha, \beta)\)-cl-DAN algortimus példa
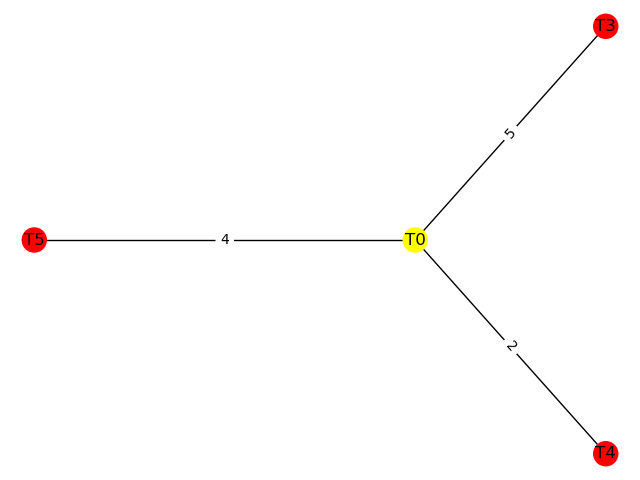
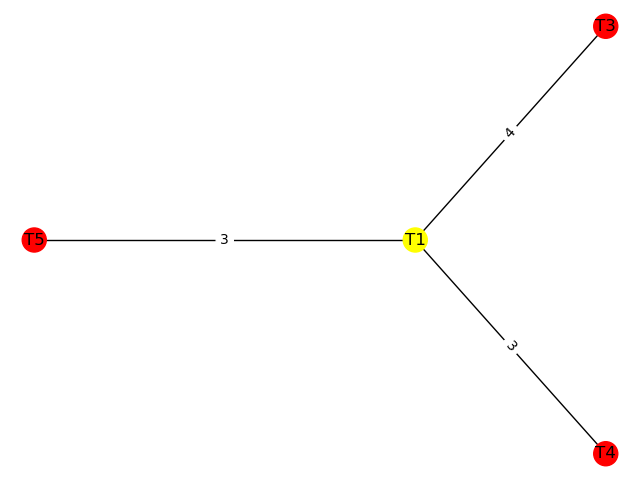
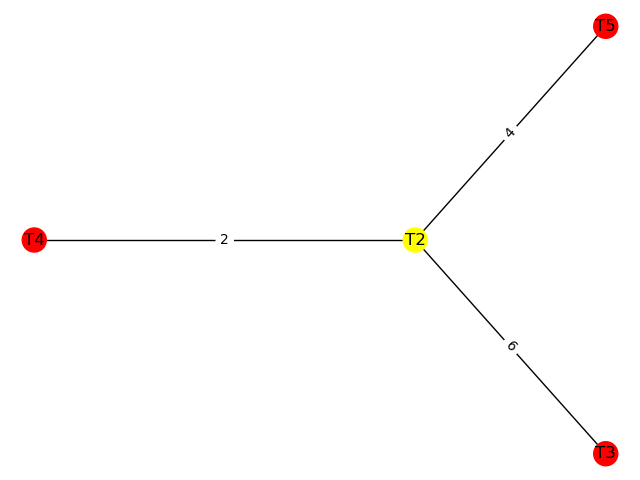
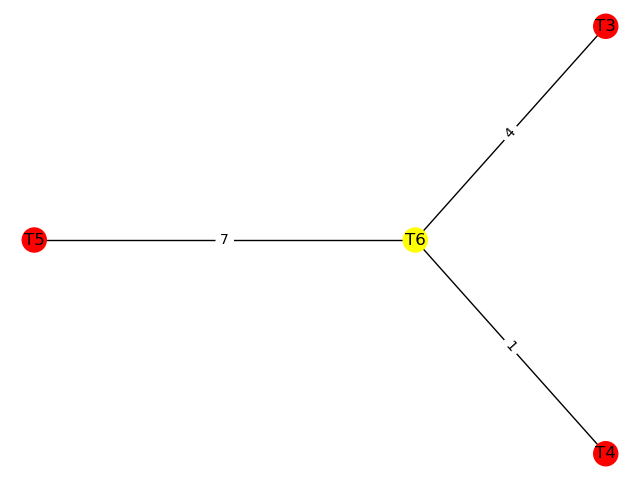
\((\alpha, \beta)\)-cl-DAN algortimus példa
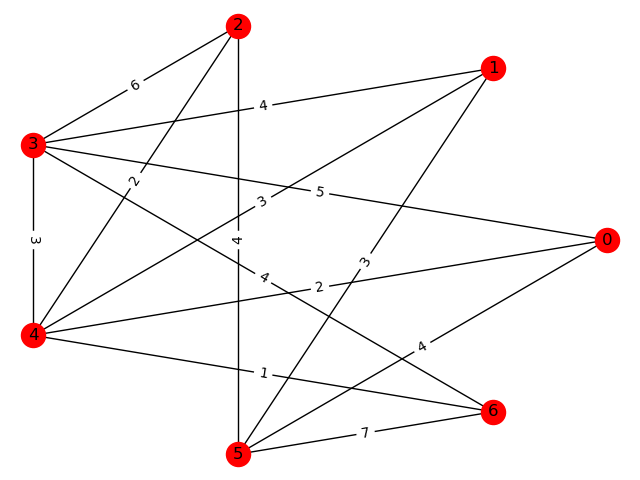
Véletlen gráfok
- Barabási-Albert modell, komplex hálózatok egy modellje,
- "preferential attachment", az újonnan becsatlakozó csomópontnak m már a hálózatban szereplő csomópontra kell kapcsolódnia

Véletlen gráfok
- 2. Erdős-Rényi modell
- az \(n\) csúcsú gráf éleit \(p\) valószínűséggel húzunk be bármely két csúcs között, egymástól függetlenül.

Véletlen gráfok
- 3. Csillaggráf
- \(n\) csúcs esetén van egy központi csúcs a gráfban, amivel a maradék \(n-1\) csúcs kapcsolatban áll

Kiterjesztett modell
- A diplomamunka alatt több az Egófához hasonló fa építési startégia meg lett vizsgálva:
- EgoBalance
- Huffman fa
- Sorfolytonos fa
- Random fa
- A cl-DAN algorimtus is kapott egy módosítást arra, hogy hogyan sorolja be a magas és alacsony halmazokat
EgoBalance
- Az cl-DAN algoritmus csere lépésének módosítása
- A cseréljük ki a szükséges csúcsokat, de mikor a szülő nélkül gyerekeket akarjuk visszacsatlakoztatni a gráfra, használjuk ki az EgoFa tulajdonságát, ami torlódásra nézve optimálisan szúrja be az elemeket
Huffman fa
- Vegyük a gyökérhez kapcsolódó csúcsok valószínűségét egy vektorba
- Rendezzük a vektort növekvő sorrendbe
- Vonjuk össze a vektor legelső két elemét, majd helyezzük vissza a vektorba és rendezzük újra növekvő sorrendbe
- Ezt addig csináljuk amíg az elemek száma nem éri el a maximális fokszámotát - Elkészült a Huffman fa
-
Köztes csomópontokat töltsük ki
- A gyökérre kapcsolódó ágakon gyujtsük össze az összes levelet
- Rendezzük sorba a leveleket nehézség szerint csökkeno sorrendbe
- Építsünk teljes fát az ágon
\( \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}\)
s
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\((.04)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\((.04)\)
\((.09)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\((.04)\)
\((.09)\)
\((.16)\)
\((.20)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\((.04)\)
\((.09)\)
\((.16)\)
\((.20)\)
\((.20)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\((.04)\)
\((.09)\)
\((.16)\)
\((.20)\)
\((.20)\)
\((.36)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\((.04)\)
\((.09)\)
\((.16)\)
\((.20)\)
\((.20)\)
\((.36)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\((.02)\)
\((.04)\)
\((.09)\)
\((.16)\)
\((.20)\)
\((.20)\)
\((.36)\)
\( \{\}\)
s
\(p_1(.24)\)
\(p_2(.20)\)
\(p_3(.10)\)
\(p_4(.10)\)
\(p_5(.10)\)
\(p_6(.10)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
\(S_1 = .24\)
\(S_2 = .20\)
\(S_3 = .20\)
\(S_4 = .36\)
Sorfolytonos és Random fa
- Vegyük a gyökérhez kapcsolódó csúcsok valószínűségét egy vektorba
- Rendezzük a vektort csökkenő sorrendbe
- Random fa esetén keverjük meg a vektor elemeit
- Építsünk teljes fát, ahol csomópont kapcsolódik a gyökér elemre
\( \{.24, .2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}\)
s
\( \{.2, .1, .1, .1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\( \{.1, .1, .1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\( \{.1, .1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
\( \{.1, .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .24\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
\(S_4 = .10\)
\(p_4(.10)\)
\( \{ .1, .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .34\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
\(S_4 = .10\)
\(p_4(.10)\)
\(p_5(.1)\)
\( \{ .07, .05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .44\)
s
\(S_2 = .20\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
\(S_4 = .10\)
\(p_4(.10)\)
\(p_5(.1)\)
\(p_6(.1)\)
\( \{.05, .02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .44\)
s
\(S_2 = .27\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
\(S_4 = .10\)
\(p_4(.10)\)
\(p_5(.1)\)
\(p_6(.1)\)
\(p_7(.07)\)
\( \{.02, .01, .01\}\)
\(p_1(.24)\)
\(S_1 = .44\)
s
\(S_2 = .32\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .10\)
\(S_4 = .10\)
\(p_4(.10)\)
\(p_5(.1)\)
\(p_6(.1)\)
\(p_7(.07)\)
\(p_8(.05)\)
\( \{.01, .01\}\)
\(p_1(.24)\)
\(S_1 = .44\)
s
\(S_2 = .32\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .12\)
\(S_4 = .10\)
\(p_4(.10)\)
\(p_5(.1)\)
\(p_6(.1)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\( \{.01\}\)
\(p_1(.24)\)
\(S_1 = .44\)
s
\(S_2 = .32\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .13\)
\(S_4 = .10\)
\(p_4(.10)\)
\(p_5(.1)\)
\(p_6(.1)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\( \{\}\)
\(p_1(.24)\)
\(S_1 = .44\)
s
\(S_2 = .32\)
\(p_2(.20)\)
\(p_3(.10)\)
\(S_3 = .13\)
\(S_4 = .11\)
\(p_4(.10)\)
\(p_5(.1)\)
\(p_6(.1)\)
\(p_7(.07)\)
\(p_8(.05)\)
\(p_9(.02)\)
\(p_{10}(.01)\)
\(p_{11}(.01)\)
Módosított fa építés
- Az első lépése a cl-DAN algoritmikusnak a csúcsok besorolása
- A cikk szerint osszuk fel fele-fele arányban, de az alacsonyak ne haladják meg a \(2\rho\) fokszámot
- A módosított itt változtat, hogy csak azok kerüljenek magas csúcsok közé, amik elérik a \(2\rho\) fokszámot
- Ezzel csökken a megépítendő fák mennyisége
- Csillaggráf esetén jelentős a változás
Eredmények
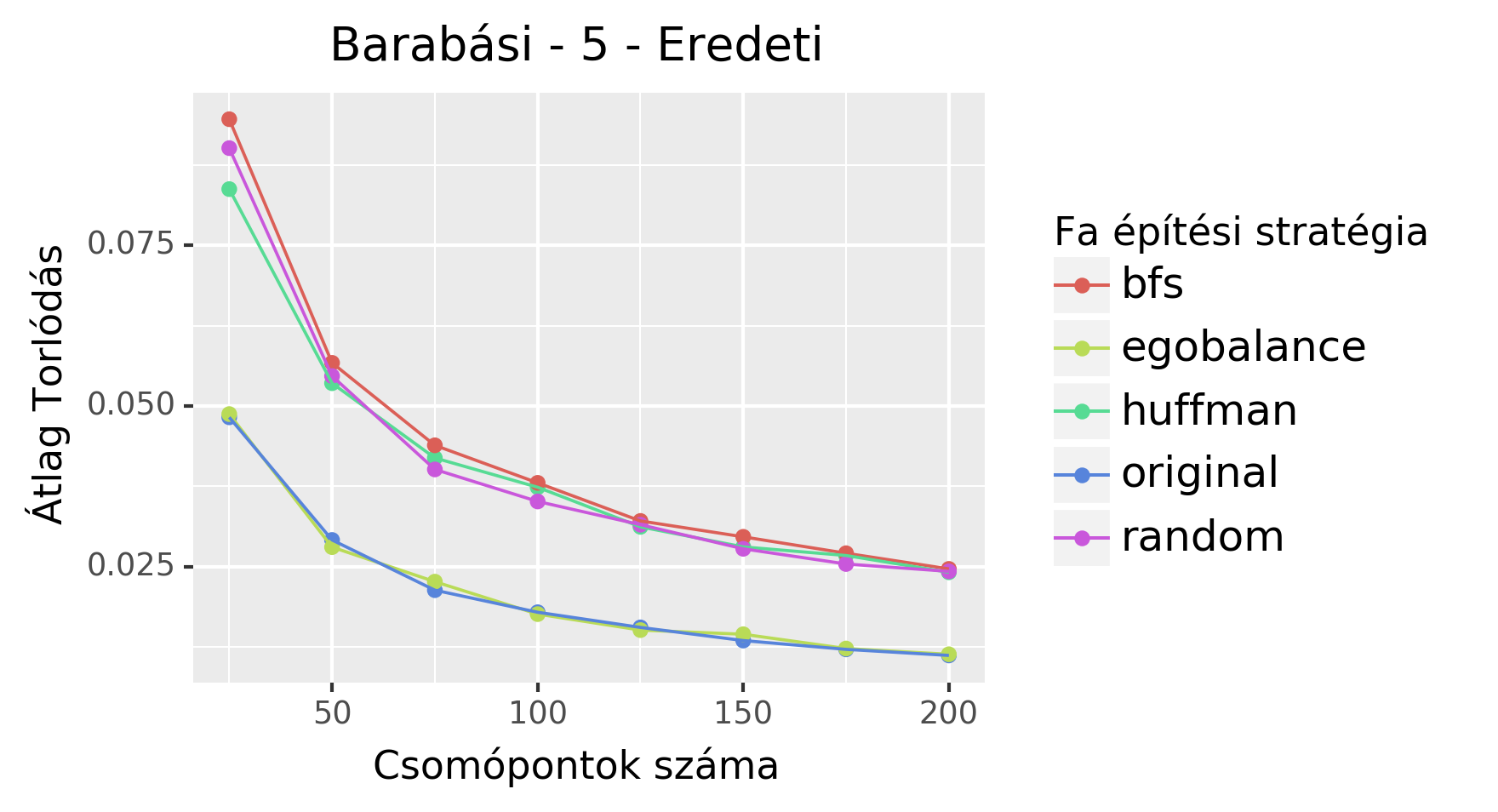
Eredmények

Eredmények


Eredmények


Köszönöm a figyelmet!
Copy of Formagol igény tudatos hálózat tervezés Full
By Imre Secodi
Copy of Formagol igény tudatos hálózat tervezés Full
- 136



