19BIO201
Intelligence in Biological Systems - 3
Reversable Reactions
19BIO201
Intelligence in Biological Systems - 3
Aadharsh Aadhithya - CB.EN.U4AIE20001
Anirudh Edpuganti - CB.EN.U4AIE20005
Madhav Kishor - CB.EN.U4AIE20033
Onteddu Chaitanya Reddy - CB.EN.U4AIE20045
Pillalamarri Akshaya - CB.EN.U4AIE20049
Team-1
Reversible vs Irreversible
Reactions
Irreversible Reactions
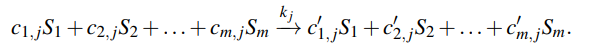
Reversible Reactions

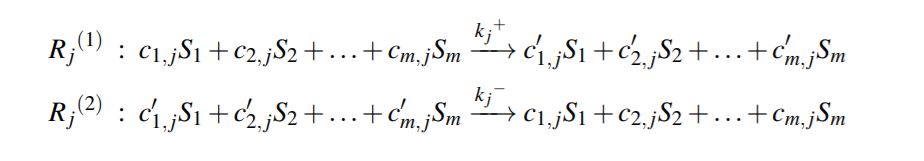
Reversible Reaction j , can be split into two irreversible reactions as
Reactions with molecularity three are very rare, due to the high improbability of having three molecular entities simultaneously colliding and forming a correct configuration that leads to the constitution of a molecular complex
Model
Reversable Reaction
Irreversable Reaction
Chemical Model
Reversable Reaction
Irreversable Reaction
Mathematical Model
ODE's
Mathematical Model
ODE's
Stochastic
Text
The stochastic approach is typically argued on the basis of physical difficulties
of ODE-based models with small populations, or in terms of the network being
too complex to describe in a deterministic way.
The stochastic formulation of a biochemical reaction network assumes
homogeneity of substances and thermal equilibrium. In this case,
the model is usually described mathematically as a continuous-time Markov chain.
Each species of the model becomes a time-dependent discrete stochastic variable indicating the
number of individuals in that species, where time is modeled as a continuous variable.
Formally, a stochastic process, {X(t),t ≥ 0}, is a continuous-time Markov chain if,
for all s,t ≥ 0, the following property is satisfied:
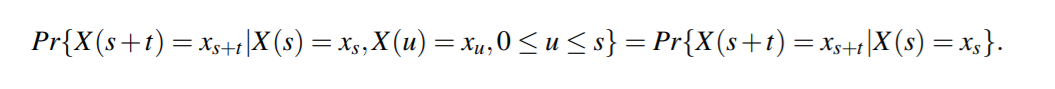
Stochastic Based Models
Given a vector of non-negative integers X = (X1,X2,...,Xm)
and species S1,S2,...,Sm the grand probability function of the model,
Pr(X,t), is the probability that there are X1 species S1, X2 species S2, ..., Xm species Sm at time t.
We consider all species to be distributed randomly and homogeneously in the volume V. The central hypothesis for the stochastic formulation of chemical kinetics is that the probability of a particular combination of reactants to react according to a given reaction R in the next infinitesimal time interval (t,t +dt) is credit, for a certain constant cR, called the stoichiometric constant of the reaction
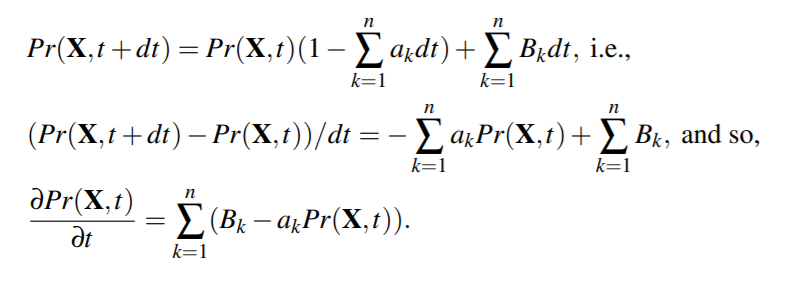
ODE Based Models
The deterministic framework of ordinary differential equations (ODEs) is often chosen as the default mathematical counterpart of a reaction-based system, sometimes followed-up by other modeling approaches
The basic quantities describing the ODE model are the concentrations [S1], [S2], ..., [Sm] of the m species in the model, and the fluxes v1, v2,..., vn of the n reactions in the model
Without loss of generality, we will assume that all reactions are reversible; an irreversible reaction is then a particular case, where one of the two kinetic constants is zero
Each species Si of the reaction model can be modeled as a function [Si ] : R+ → R+ representing the time evolution of its concentration. The dependencies between the species can then be expressed in terms of a systems of ODEs in the variables [Si ] modeling the change in [Si ] as a function of all other variables
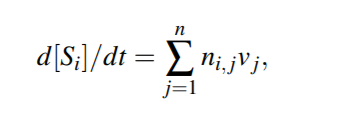
we make the assumption that the only factor affecting the concentrations of the species is the reactions. Considering the vector of all reaction fluxes v = (v1, v2,..., vn)^T , the ODE representation of the entire reaction model can be written in a compact way as follows
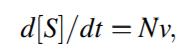
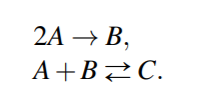
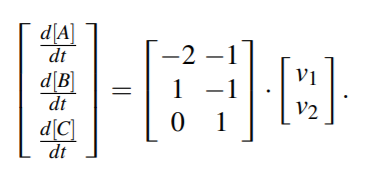
Text
Two mostly used reaction kinetics are
- Mass Action Principle
- Michaelis-Menten kinetics
Law of Mass Action
The most common biochemical kinetics follow the mass action law. It states that the flux (also called sometimes rate) of a reaction is proportional to the probability of the reactants colliding
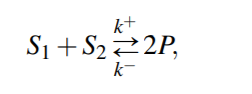
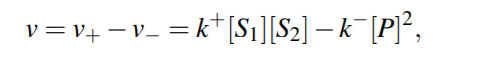
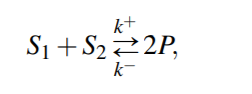
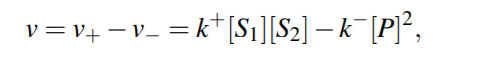
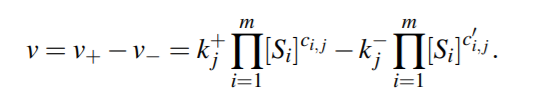
For a general reversible reaction, reaction rate is...
Corresponding system of ODE will then be
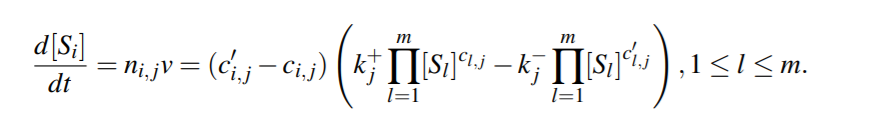
Equilibrium Constant for the reaction would be then,
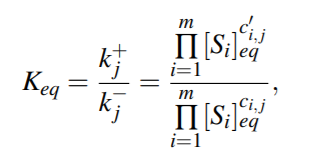
The time course for a species S is obtained by integrating the corresponding ODE. For a simple decomposition reaction S k −→ P1+P2, the time dynamics is described by the ODE d[S]/dt = −k[S].
Text
Analytical solution yields,
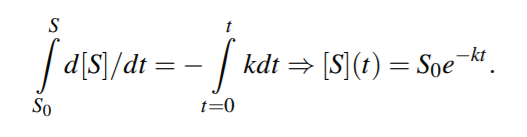
Enzymatic Reactions
Enzymatic reactions are a special class of biochemical reactions, where an enzyme is required for a reaction to take place, but the enzyme itself is not consumed during the reaction
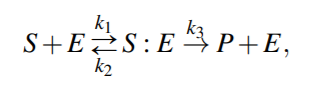
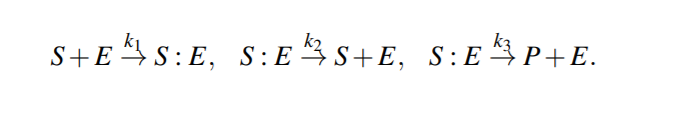
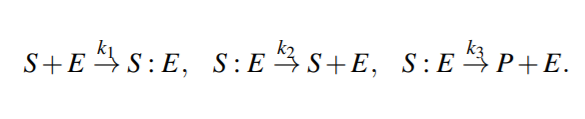
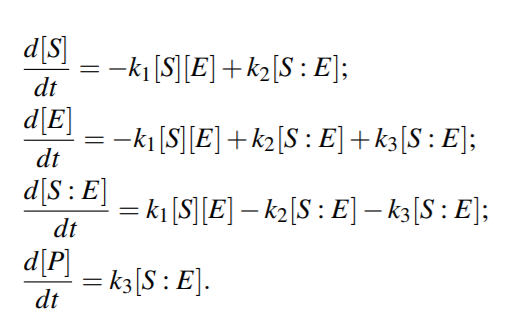
Michaelis-Menten kinetics
Because the system of ODEs cannot be solved analytically, simplifying assumptions have been proposed.
For example, the kinetic constants k1, k2 could be assumed to be much greater than k3 (k1, k2 >> k3 ), i.e. [S : E] is negligible compared to [S] and [P], because the substrate-enzyme complex concentration is very low. This is called the quasi-equilibrium between the free enzyme E and the compound S : E
The Michaelis-Menten equation relates the reaction rate v of synthesizing the product P to the concentration of the substrate, [S], by the relation
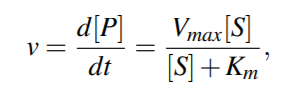
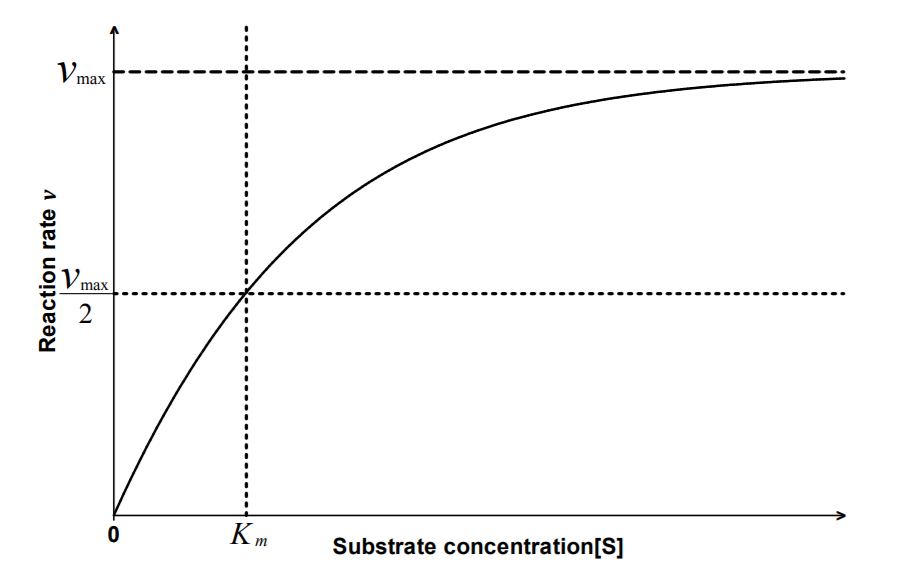
The Michaelis constant Km is the concentration of substrate
for which the reaction rate is half-maximal.
Identifying the parameters yields the connection between
the Michaelis-Menten kinetics and
the mass-action deduced kinetics of an enzymatic reaction
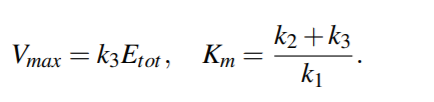
Text
Assuming the quasi-equilibrium, the quantity k3/k1 is negligible, thus Km ∼= k2/k
Reversable Michaelis-Menten kinetics
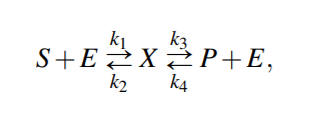
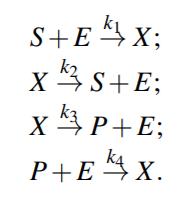
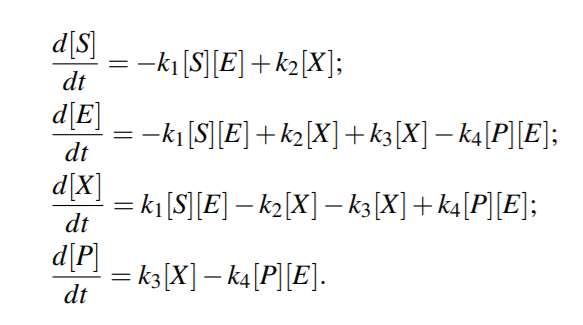
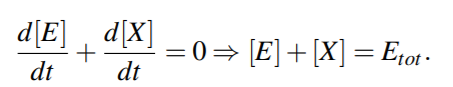
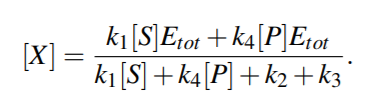
From above equations,
For quasi steady state,
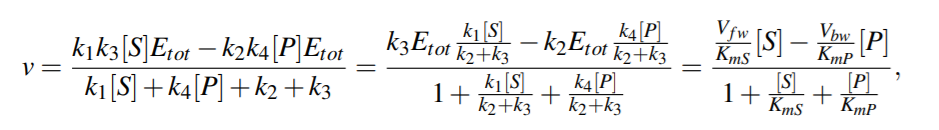
where KmS = (k2 +k3)/k1 and KmP = (k2 +k3)/k4 are the Michaelis-Menten constants (i.e. for half-maximal forward and backward rate) for the substrate and product, respectively, and Vf w(Vbw) denotes the maximal rate in forward (backward) direction.
Mass action and Michaelis-Menten are not the only existing kinetics. Some enzymatic reaction can follow Hill kinetics, Goldbeter-Koshland kinetics, or be subject to inhibition.
Bio Models
Bio Models
BioModels is a repository of mathematical models of biological and biomedical systems. It hosts a vast selection of existing literature-based physiologically and pharmaceutically relevant mechanistic models in standard formats.

Models in this database are primarily distinguished by their identifier, which is in the form BIOMDxxxxxxxxxx where the x’s represent a number
COPASI
COPASI
COmplex PAthway SImulator
COPASI
COPASI is a software application for simulation and analysis of biochemical networks and their dynamics.
COPASI is a stand-alone program that supports models in the SBML standard and can simulate their behavior using ODEs or Gillespie's stochastic simulation algorithm; arbitrary discrete events can be included in such simulations.
Each chemical species in the network is represented by an ODE that describes the rate of change of that species along time. The ODE is composed by an algebraic sum of terms that represent the rates of the reactions that affect the chemical species. For a chemical species X
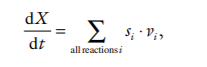
where si is a stoichiometry coefficient that is the number of molecules of X consumed or produced in one cycle of reaction i, with a positive sign if it is produced or negative if consumed, and vi is the velocity of reaction i. Obviously, for reactions that do not produce or consume X the corresponding s i is zero
These ODE models can be used to simulate the dynamics of the concentrations of the chemical species along time given their initial values. This is achieved by numerical integration of the system of ODE which can be carried out with well-established algorithms
Steady states can be found using the Newton–Raphson method which finds the roots of the right-hand side of the ODE (which must be zero by the definition of steady state). Alternatively steady states can also be found by integration of the ODE. COPASI can use either one of these strategies or a combination of the two
Thank you sir
Robotics-Interim Evaluation
By Incredeble us
Robotics-Interim Evaluation
- 138



