19AIE201
Introduction to Robotics
Evaluation 6
19AIE201
Introduction to Robotics
Aadharsh Aadhithya - CB.EN.U4AIE20001
Anirudh Edpuganti - CB.EN.U4AIE20005
Madhav Kishor - CB.EN.U4AIE20033
Onteddu Chaitanya Reddy - CB.EN.U4AIE20045
Pillalamarri Akshaya - CB.EN.U4AIE20049
Team-1
19AIE201
Introduction to Robotics
Pieper's Solution for 6-axis robots
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
Conditions
- Last three axes of manipulator must be intersecting
- All the six joints must be revolute joints
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
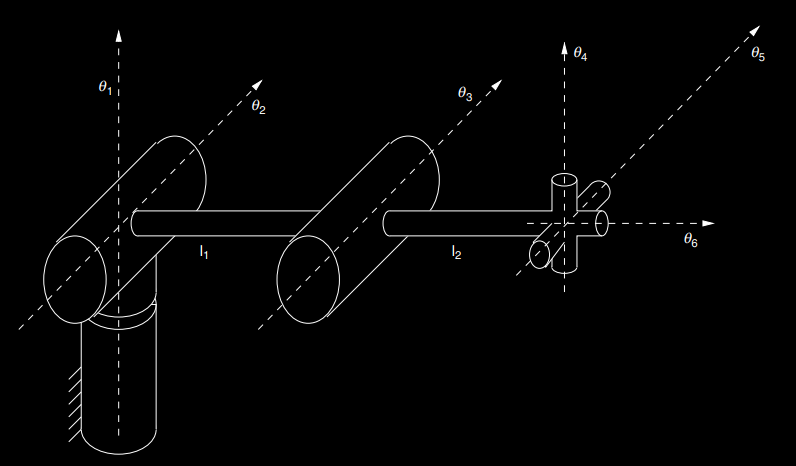
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
- The distance between the axes 1,2,3 and axes 4,5,6 only depends on
- The height of end manipulator only depends on and
θ3
\theta_3
θ2
\theta_2
θ3
\theta_3
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
a3−sin(α3)d4cos(α3)d41
\begin{bmatrix}
a_3 \\
-sin(\alpha_3)d_4\\
cos(\alpha_3)d_4\\
1 \\
\end{bmatrix}
\quad
3P4ORG=
{^3P_{4ORG}} =
where APBorg is the origin of frame B expressed in coordinate of frame A
where \ {^AP_{Borg}} \ is \ the \ origin\ of \ frame \ B \ expressed \ in \ coordinate \ of \ frame \ A
a3−sin(α3)d4cos(α3)d41
\begin{bmatrix}
a_3 \\
-sin(\alpha_3)d_4\\
cos(\alpha_3)d_4\\
1 \\
\end{bmatrix}
\quad
0P4ORG=
{^0P_{4ORG}} =
32T
^2_3T
21T
^1_2T
10T
^0_1T
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
32T=cos(θ3)sin(θ3)cos(α2)sin(θ3)sin(α2)0−sin(θ3)cos(θ3)cos(α2)cos(θ3)sin(α2)00−sin(α2)cos(α2)0a2−d3sin(α2)d3cos(α2)1
^2_3T = \begin{bmatrix}
cos(\theta_3) & -sin(\theta_3) & 0 & a_2 \\
sin(\theta_3)cos(\alpha_2) & cos(\theta_3)cos(\alpha_2) & -sin(\alpha_2) & -d_3sin(\alpha_2) \\
sin(\theta_3)sin(\alpha_2) & cos(\theta_3)sin(\alpha_2) & cos(\alpha_2) & d_3cos(\alpha_2) \\
0 & 0 & 0 & 1
\end{bmatrix}
F=f1(θ3)f2(θ3)f3(θ3)1= 32Ta3−sin(α3)d4cos(α3)d41
\vec{F} = \begin{bmatrix}
f_1(\theta_3) \\
f_2(\theta_3) \\
f_3(\theta_3) \\
1
\end{bmatrix} = \ ^2_3T \begin{bmatrix}
a_3 \\
-sin(\alpha_3)d_4\\
cos(\alpha_3)d_4\\
1 \\
\end{bmatrix}
\quad
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
32T=cos(θ3)sin(θ3)cos(α2)sin(θ3)sin(α2)0−sin(θ3)cos(θ3)cos(α2)cos(θ3)sin(α2)00−sin(α2)cos(α2)0a2−d3sin(α2)d3cos(α2)1
^2_3T = \begin{bmatrix}
cos(\theta_3) & -sin(\theta_3) & 0 & a_2 \\
sin(\theta_3)cos(\alpha_2) & cos(\theta_3)cos(\alpha_2) & -sin(\alpha_2) & -d_3sin(\alpha_2) \\
sin(\theta_3)sin(\alpha_2) & cos(\theta_3)sin(\alpha_2) & cos(\alpha_2) & d_3cos(\alpha_2) \\
0 & 0 & 0 & 1
\end{bmatrix}
F=f1(θ3)f2(θ3)f3(θ3)1= 32Ta3−sin(α3)d4cos(α3)d41
\vec{F} = \begin{bmatrix}
f_1(\theta_3) \\
f_2(\theta_3) \\
f_3(\theta_3) \\
1
\end{bmatrix} = \ ^2_3T \begin{bmatrix}
a_3 \\
-sin(\alpha_3)d_4\\
cos(\alpha_3)d_4\\
1 \\
\end{bmatrix}
\quad
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
G=g1(θ2,θ3)g2(θ2,θ3)g3(θ2,θ3)1= 21Tf1(θ3)f2(θ3)f3(θ3)1
\vec{G} = \begin{bmatrix}
g_1(\theta_2, \theta_3) \\
g_2(\theta_2, \theta_3) \\
g_3(\theta_2, \theta_3) \\
1
\end{bmatrix} = \ ^1_2T \begin{bmatrix}
f_1(\theta_3) \\
f_2(\theta_3) \\
f_3(\theta_3) \\
1
\end{bmatrix}
21T=cos(θ2)sin(θ2)cos(α1)sin(θ2)sin(α1)0−sin(θ2)cos(θ2)cos(α1)cos(θ2)sin(α1)00−sin(α1)cos(α1)0a1−d2sin(α1)d2cos(α1)1
^1_2T = \begin{bmatrix}
cos(\theta_2) & -sin(\theta_2) & 0 & a_1 \\
sin(\theta_2)cos(\alpha_1) & cos(\theta_2)cos(\alpha_1) & -sin(\alpha_1) & -d_2sin(\alpha_1) \\
sin(\theta_2)sin(\alpha_1) & cos(\theta_2)sin(\alpha_1) & cos(\alpha_1) & d_2cos(\alpha_1) \\
0 & 0 & 0 & 1
\end{bmatrix}
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
12T=cos(θ2)sin(θ2)cos(α1)sin(θ2)sin(α1)0−sin(θ2)cos(θ2)cos(α1)cos(θ2)sin(α1)00−sin(α1)cos(α1)0a1−d2sin(α1)d2cos(α1)1
12T=cos(θ2)sin(θ2)cos(α1)sin(θ2)sin(α1)0−sin(θ2)cos(θ2)cos(α1)cos(θ2)sin(α1)00−sin(α1)cos(α1)0a1−d2sin(α1)d2cos(α1)1
^2_1T = \begin{bmatrix}
cos(\theta_2) & -sin(\theta_2) & 0 & a_1 \\
sin(\theta_2)cos(\alpha_1) & cos(\theta_2)cos(\alpha_1) & -sin(\alpha_1) & -d_2sin(\alpha_1) \\
sin(\theta_2)sin(\alpha_1) & cos(\theta_2)sin(\alpha_1) & cos(\alpha_1) & d_2cos(\alpha_1) \\
0 & 0 & 0 & 1
\end{bmatrix}
10T=cos(θ1)sin(θ1)00−sin(θ1)cos(θ1)0000100001
^0_1T = \begin{bmatrix}
cos(\theta_1) & -sin(\theta_1) & 0 & 0 \\
sin(\theta_1) & cos(\theta_1) & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
0P4ORG=cos(θ1)g1(θ2,θ3)−sin(θ1)g2(θ2,θ3)sin(θ1)g1(θ2,θ3)+cos(θ1)g2(θ2,θ3)g3(θ2,θ3)1
{^0P_{4ORG}} = \begin{bmatrix}
cos(\theta_1)g_1(\theta_2,\theta_3) - sin(\theta_1)g_2(\theta_2,\theta_3) \\
sin(\theta_1)g_1(\theta_2,\theta_3) + cos(\theta_1)g_2(\theta_2,\theta_3) \\
g_3(\theta_2,\theta_3)\\
1 \\
\end{bmatrix}
\quad
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
Case Number 1 a1=0This will be the case when the axes 1 and 2 intersect
Case \ Number \ 1 \: \ a_1 = 0 \\
This\ will \ be \ the\ case \ when \ the \ axes \ 1 \ and \ 2 \ intersect
r2=t142+t242+t342=f12(θ3)+f22(θ3)+f32(θ3)+d22+2d2f3(θ3)
r^2=t^2_{14}+t^2_{24}+t^2_{34}=f^2_1(\theta_3)+f^2_2(\theta_3)+f^2_3(\theta_3)+d^2_2+2d_2f_3(\theta_3)
Simplifying the above equation we get the value of θ3Subsutituting the value of θ3 in the equations we get θ1 θ2
Simplifying \ the \ above \ equation \ we \ get \ the \ value \ of \ \theta_3 \\
Subsutituting \ the \ value \ of \ \theta_3 \ in \ the \ equations \ we \ get \ \theta_1 \ \theta_2
63Tdes=30T−1 60Tdes
^3_6T_{des} = ^0_3T^{-1} \ ^0_6T_{des}
Now solving the above matrix we get the values of θ4, θ5, θ6
Now \ solving \ the \ above \ matrix \ we \ get \ the \ values \ of \ \theta_4, \ \theta_5, \ \theta_6
19AIE201
Introduction to Robotics
Piper's Solution for 6-axis robots
Case \ Number \ 2 \: \ \alpha_1 = 0 \\
The \ height \ of \ the \ spherical \ wrist \ centre \ in \ the \ 0 \ frame \ will \ be \
g3(θ2,θ3)=sin(θ2)sin(α1)f1(θ3)+cos(θ2)sin(α1)f2(θ3)+cos(α1)f3(θ3)+d2cos(α1)
g_3(\theta_2,\theta_3) = sin(\theta_2)sin(\alpha_1)f_1(\theta_3) + cos(\theta_2)sin(\alpha_1)f_2(\theta_3) + cos(\alpha_1)f_3(\theta_3) + d_2cos(\alpha_1)
g3(θ3)=f3(θ3)+d2
g_3(\theta_3) = f_3(\theta_3) + d_2
Simplifying the above equation we get the value of θ3Subsutituting the value of θ3 in the above equation we get θ1 θ2
Simplifying \ the \ above \ equation \ we \ get \ the \ value \ of \ \theta_3 \\
Subsutituting \ the \ value \ of \ \theta_3 \ in \ the \ above \ equation \ we \ get \ \theta_1 \ \theta_2
63Tdes=30T−1 60Tdes
^3_6T_{des} = ^0_3T^{-1} \ ^0_6T_{des}
Now solving the above matrix we get the values of θ4, θ5, θ6
Now \ solving \ the \ above \ matrix \ we \ get \ the \ values \ of \ \theta_4, \ \theta_5, \ \theta_6
19AIE201
Introduction to Robotics
Newton-Raphson method
19AIE201
Introduction to Robotics
Newton-Raphson method
Newton-Raphson method
60Tθ= 60T(θ1,θ2,θ3,θ4,θ5,θ6)
^0_6T_{\theta} = \ ^0_6T(\theta_1,\theta_2,\theta_3,\theta_4,\theta_5,\theta_6)
60Tdes is a final orientation matrix of end effector
^0_6T_{des} \ is \ a \ final \ orientation \ matrix \ of \ end \ effector \\
Let 60Tθ(a,b) denote the element of matrix 60Tθ that is in the ath row and bth column
Let \ ^0_6T_{\theta}(a,b) \ denote \ the \ element \ of \ matrix \ ^0_6T_{\theta} \ that \ is \ in \ the \ ath \ row \ and \ bth \ column
θ= 60Tθ−60Tdes
\theta = \ ^0_6T_{\theta} - ^0_6T_{des}
Newton-Raphson method
θn+1=θn−F′(θn)F(θn)
\theta_{n+1} = \theta_n - \frac{F(\theta_n)}{F'(\theta_n)}
Newton-Raphson method
θn+1=θn−F′(θn)F(θn)
\theta_{n+1} = \theta_n - \frac{F(\theta_n)}{F'(\theta_n)}
θn+1=θn−J(θn)−1F(θn)
\theta_{n+1} = \theta_n - J(\theta_n)^{-1}F(\theta_n)
Newton-Raphson method
θn+1=θn−J(θn)−1F(θn)
\theta_{n+1} = \theta_n - J(\theta_n)^{-1}F(\theta_n)
Jacobian Matrix
19AIE201 Introduction to Robotics Evaluation 6
Robotics A5
By Incredeble us
Robotics A5
- 68
