Hidden Markov Model
19MAT117
Aadharsh Aadhithya - CB.EN.U4AIE20001
Anirudh Edpuganti - CB.EN.U4AIE20005
Madhav Kishore - CB.EN.U4AIE20033
Onteddu Chaitanya Reddy - CB.EN.U4AIE20045
Pillalamarri Akshaya - CB.EN.U4AIE20049
Team-1
Hidden Markov Model
19MAT117
Markov chains
19MAT117
Markov chains



19MAT117
Markov chains
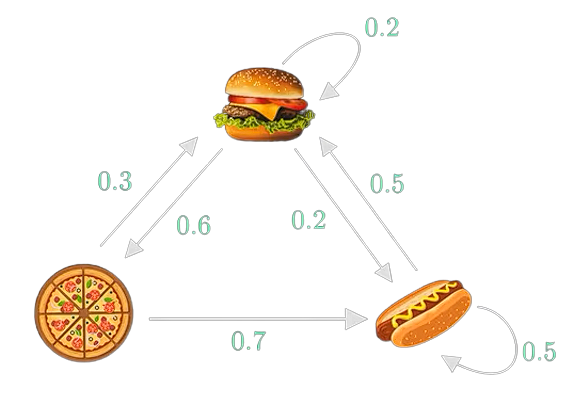
Markov chains




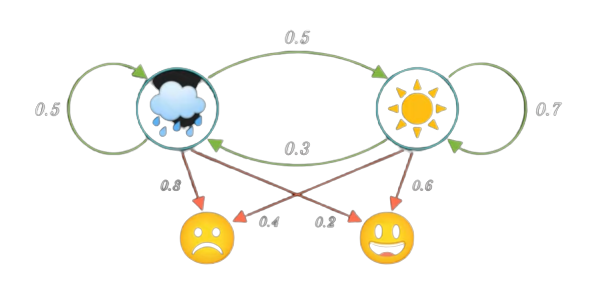
Hidden Markov Model
Hidden Markov Model

Hidden Markov Model
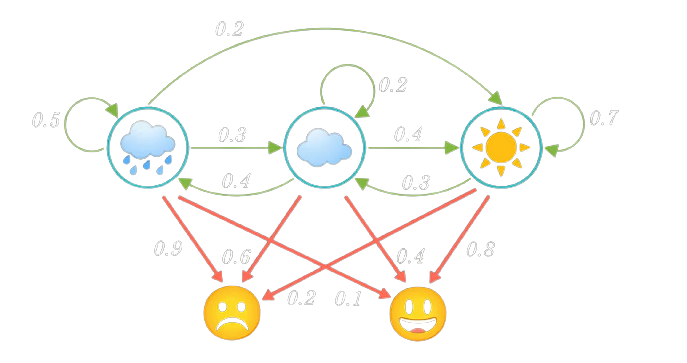
Hidden Markov Model
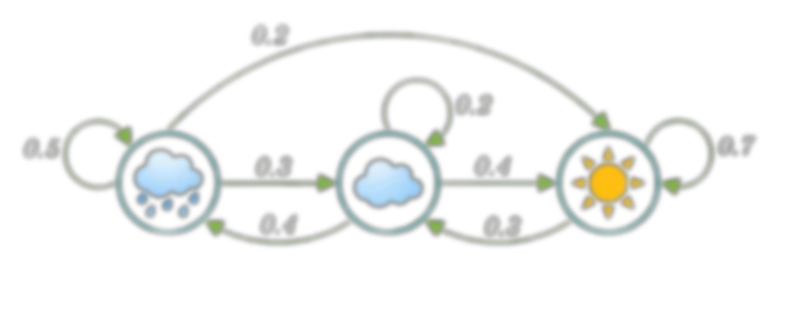
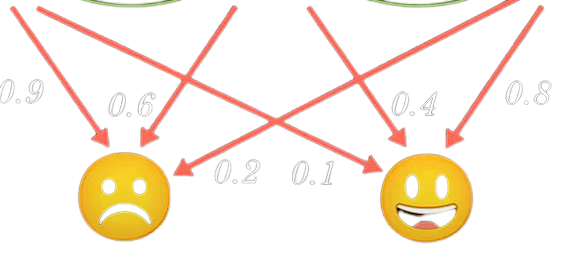
Hidden Markov Model











Hidden Markov Model
Hidden Markov Model
Problems
Hidden Markov Model
Problems
Problem 1
Problem 1



Forward Algorithm
Forward Algorithm



S
S
S
R
R
R

Forward Algorithm



S
S
S
R
R
R

Forward Algorithm



S
S
S
R
R
R

Forward Algorithm



S
S
S
R
R
R

Forward Algorithm



S
S
S
R
R
R




Problem 2
Problem 2
Problem 2
Problem 2



Problem 2



Solution
Viterbi Algorithm
Veterbi Algorithm



S
S
S
R
R
R

Veterbi Algorithm



S
S
S
R
R
R

Veterbi Algorithm



S
S
S
R
R
R

Veterbi Algorithm



S
S
S
R
R
R

Veterbi Algorithm



S
S
R
R
R

Veterbi Algorithm



S
S
R
R
R

Veterbi Algorithm



S
R
R
R

Veterbi Algorithm



S
R
R
R

Veterbi Algorithm



S
R
R

Veterbi Algorithm



S
R
R
Veterbi Algorithm
S
R
R



Veterbi Algorithm



Problem 3
Expected Number of Transitions
From State i to j
Expected Number of transitions from state Si
Iteratively Calculate A,B
Converges to a local maxima
Iteratively Calculate A,B
Converges to a local maxima
Baum Welch Algorithm, is a type of Expectation Maximisation
Credit Card fraud detection
Credit Card fraud detection

Credit Card fraud detection





₹100
₹200
₹500
₹1000
₹7000
Credit Card fraud detection





₹100
₹200
₹500
₹1000
₹7000
Observation
Seq.
Credit Card fraud detection





₹100
₹200
₹500
₹1000
₹7000
Credit Card fraud detection





₹100
₹200
₹500
₹1000
₹7000
Naively We can Observe, Given the observation sequence,Probability of a high transaction is low
Credit Card fraud detection





₹100
₹200
₹500
₹1000
₹7000
What if, we can learn from history?
The Process can be modeled as a Markov Process
The Process can be modeled as a Markov Process
Further, Since we aren't sure about the states causing the Observation,It should be modelled as Hidden Markov Model
Learning...Hmm....?🤔
Baum Welch Algorithm comes to the rescue
After Learning the Parameters of HMM, We can find the probability of a sequence of observations, Given the Model which is our Forward Algorithm
Credit Card fraud detection





₹100
₹200
₹500
₹1000
₹7000

₹20000
19MAT117
Applications and Future Learning Directions
Applications
- Sequence Alignment in Biology
- Widely Used in NLP
- Inference from Time Series
- Molecular Evolutionary models
- Phylogenitcs
Applications
Future Learning Directions
- Generalizations of HMM - Bayesian Networks
- Continuous-Time Markov Models
- Other methods of Expectation-Maximization for learning
References
[3] djp3, Hidden Markov Models 12: the Baum-Welch algorithm, (Apr. 10, 2020). Accessed: Jan. 17, 2022. [Online]. Available: https://www.youtube.com/watch?v=JRsdt05pMoI
[5] “Markov Chains Clearly Explained! - YouTube.” https://www.youtube.com/ (accessed Jan. 17, 2022).
[4] Normalized Nerd, Hidden Markov Model Clearly Explained! Part - 5, (Dec. 26, 2020). Accessed: Jan. 17, 2022. [Online]. Available: https://www.youtube.com/watch?v=RWkHJnFj5rY
[2] L. R. Rabiner, “A tutorial on hidden Markov models and selected applications in speech recognition,” Proceedings of the IEEE, vol. 77, no. 2, pp. 257–286, Feb. 1989, doi: 10.1109/5.18626.
[1] “(14) (PDF) A revealing introduction to hidden markov models.” https://www.researchgate.net/publication/288957333_A_revealing_introduction_to_hidden_markov_models (accessed Jan. 17, 2022).
Thank you Mam
MIS-3
By Incredeble us
MIS-3
- 158



