Deep Learning for Signal and Image Processing

Team 01

Assignment 1a,1b,1c

Assignment 1a

Dataset Familiarization

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
import pandas as pd
import matplotlib.pyplot as plt

# Load the iris data from a given CSV file into a data frame (data_iris)
data_iris = pd.read_csv('/content/iris.csv')

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
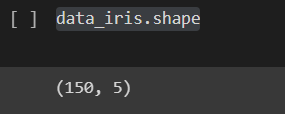
Shape of data
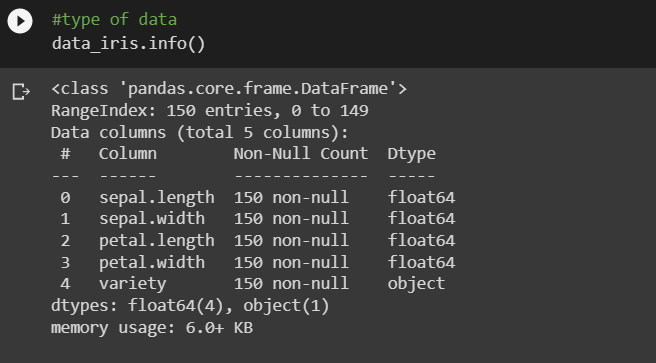
Type of data

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
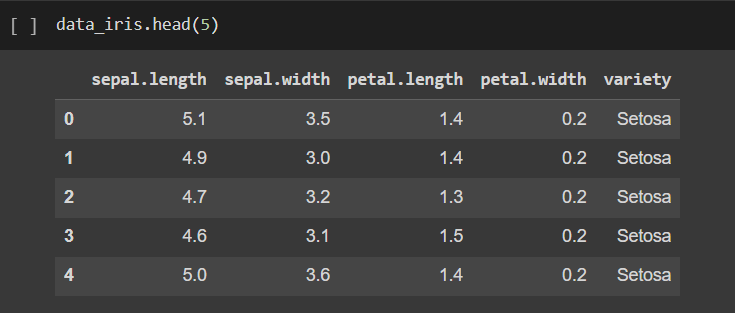
first 5 rows with labels
Find the keys

Not Applicable, since we loadded the data from csv file. However, sklearns load data gives the result in a dict

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
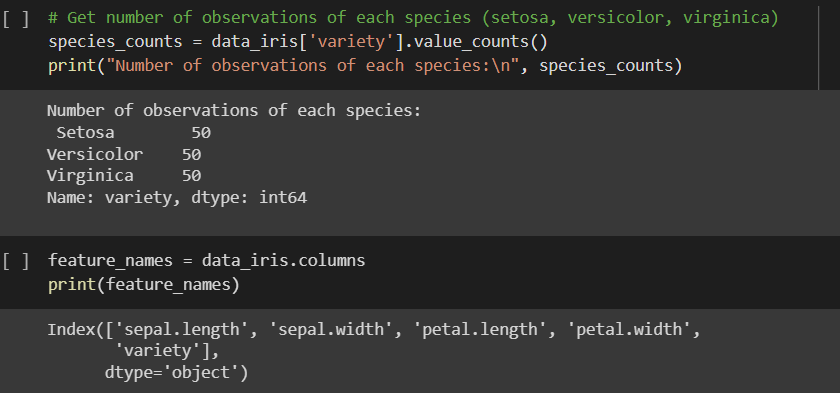
find number of features and feature names

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
Description of Iris data

The iris dataset is a classic multivariate dataset used for classification and data analysis. It contains measurements of various attributes of three different species of iris flowers: Setosa, Versicolor, and Virginica. The measurements include the length and width of the sepals and petals, in centimeters.

 

The dataset consists of 150 samples, with 50 samples per species, and is widely used in machine learning and statistical analysis as a benchmark dataset. It was first introduced in 1936 by the British statistician and biologist Ronald Fisher, and has since become a popular example in the fields of pattern recognition, data visualization, and exploratory data analysis.

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
number of categories/class labels in the data

get the missing values and nan values (with feature and class label indexing).

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
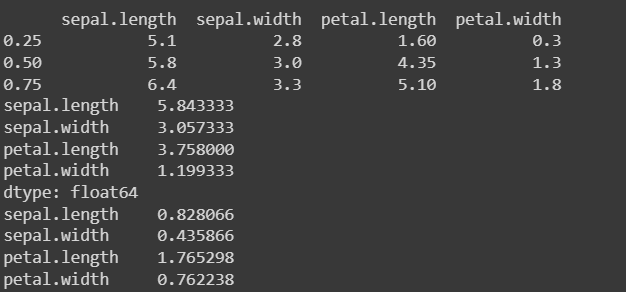
view basic statistical details like percentile, mean, std etc. of iris data

percentiles = data_iris.quantile([0.25, 0.5, 0.75])

mean = data_iris.mean()

std_dev = data_iris.std()

print(percentiles)
print(mean)
print(std_dev)

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
view basic statistical details like percentile, mean, std etc. of iris data

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
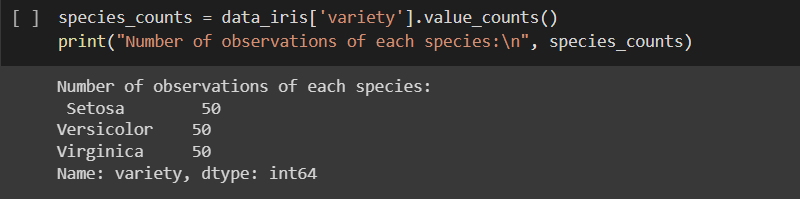
get number of observations of each species (setosa, versicolor, virginica) from iris data and create sub data frames for each species (data_iris_setosa, data_iris_versicolor, data_iris_virginica)

# Create sub data frames for each species
data_iris_setosa = data_iris[data_iris['variety'] == 'Setosa']
data_iris_versicolor = data_iris[data_iris['variety'] == 'Versicolor']
data_iris_virginica = data_iris[data_iris['variety'] == 'Virginica']

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
drop Id column from data_iris Dataframe and create a new data frame with this modified part.

data_iris_modified = data_iris.drop(columns=['variety']).reset_index()
create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column). create a Bar plot and a Pie plot to get the frequency of the three species of the Iris data create a graph to find the relationship between the sepal length and sepal width of different species (scatter plot , give different color labels for different species)

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
 create a Bar plot and a Pie plot to get the frequency of the three species of the Iris data.

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
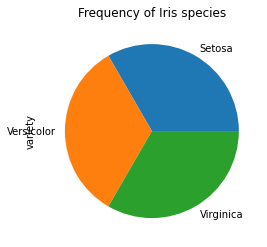
 create a Bar plot and a Pie plot to get the frequency of the three species of the Iris data.

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
create a graph to find the relationship between the sepal length and sepal width of different species (scatter plot , give different color labels for different species)

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

Assignment 1a

Dataset Familiarization

Python program to load the iris data from a given CSV file into a data frame (data_iris)
create a graph to find the relationship between the sepal length and sepal width of different species (scatter plot , give different color labels for different species)

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

# Create a graph to find the relationship between the sepal length and sepal width of different species (scatter plot, give different color labels for different species)
plt.scatter(data_iris_setosa['sepal.length'], data_iris_setosa['sepal.width'], color='red', label='Iris-setosa')
plt.scatter(data_iris_versicolor['sepal.length'], data_iris_versicolor['sepal.width'], color='green', label='Iris-versicolor')
plt.scatter(data_iris_virginica['sepal.length'], data_iris_virginica['sepal.width'], color='blue', label='Iris-virginica')
plt.title('Relationship between sepal length and sepal width of Iris species')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.legend()
plt.show()

Assignment 1a

Dataset Familiarization

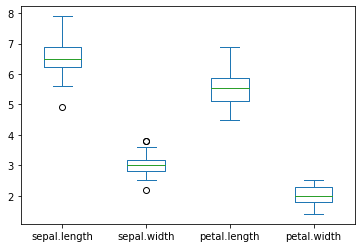
create a graph to see how the feature (SepalLength, SepalWidth, PetalLength, PetalWidth) are distributed for each species. Comment on it.

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

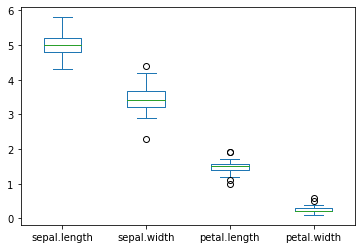
Setosa

versicolor

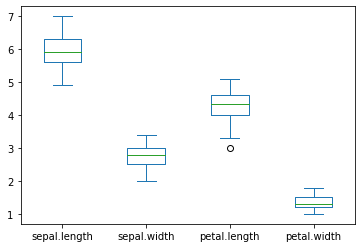
virginica

Assignment 1a

Dataset Familiarization

create a pairplot of the iris data set and check which flower speciesseems to be the most separable. Comment on it.

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

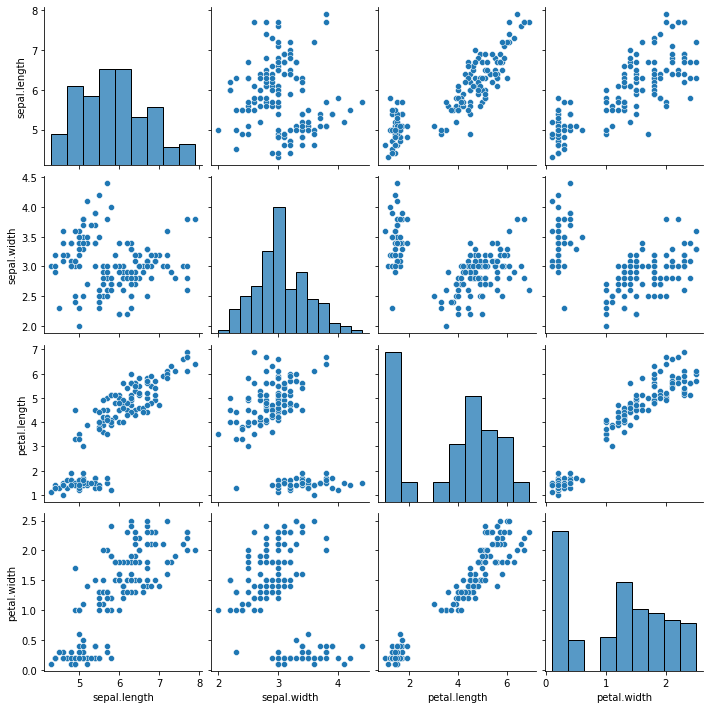
Assignment 1a

Dataset Familiarization

find the correlation between variables of iris data (between features and between feature and species). Also create a heatmap using Seaborn to present their relations

# Create two date frames data_iris_feature (only with feature columns) and data_iris_species (only with species column)
data_iris_species = data_iris['variety']


# Create a Bar plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='bar')
plt.title('Frequency of Iris species')
plt.xlabel('Species')
plt.ylabel('Frequency')
plt.show()

# Create a Pie plot to get the frequency of the three species of the Iris data
species_counts.plot(kind='pie')
plt.title('Frequency of Iris species')
plt.show()

data_iris_modified= data_iris_modified.drop(["index"],axis=1)
correlation = data_iris_modified.corr()
sns.heatmap(correlation)

Assignment 1b

Linear Regression

Assignment 1b

Linear Regression

Create a complete document on Linear Regression model representation cost function Gradient descent algorithm Python program for linear regression (single and multi-variable)

Assignment 1b

Linear Regression(Simple)

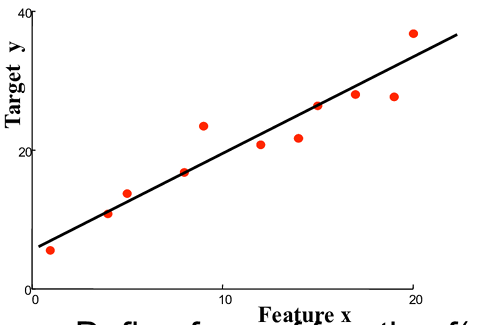
Evaluate line y = mx+c 

where,  m is the slope of the line 

c is the y_intercept 

Assignment 1b

Linear Regression(Simple)

Evaluate line y = mx+c 

where,  m is the slope of the line 

c is the y_intercept 

Assignment 1b

Linear Regression(Multivariate)

y^(x)=θ0+θ1x1+θ2x2+…+θnxn\hat{y}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{n} x_{n}
\hat{y}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{n} x_{n}

 This can be represented in Matrix-Vector Form as

y^(x)=θxnTθ=[θ0,…,θn]x=[1,x1,…,xn]\hat{y}(x)=\theta x_{n}^{T} \\ \theta=\left[\theta_{0}, \ldots, \theta_{n}\right] \\ x=\left[1, x_{1}, \ldots, x_{n}\right]
\hat{y}(x)=\theta x_{n}^{T} \\ \theta=\left[\theta_{0}, \ldots, \theta_{n}\right] \\ x=\left[1, x_{1}, \ldots, x_{n}\right]

Our aim now is to learn Theta Vector

Assignment 1b

Geometrical Meaning: Optimization POV

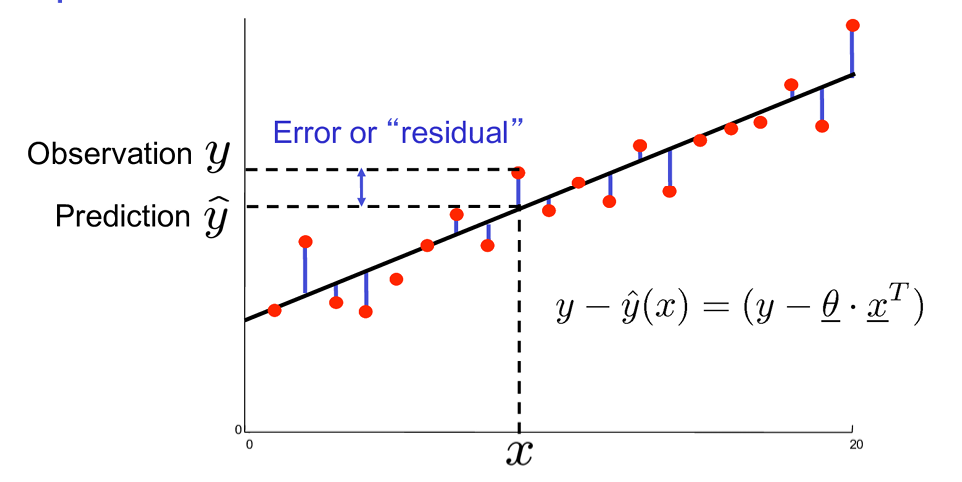
Assignment 1b

Geometrical Meaning: Optimization POV

Cost Function

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2
J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2

where m is the number of training examples, h() is the predicted value for the i-th example, and y^i is the actual value for the i-th example.

Assignment 1b

Geometrical Meaning:  Linear Algebra POV

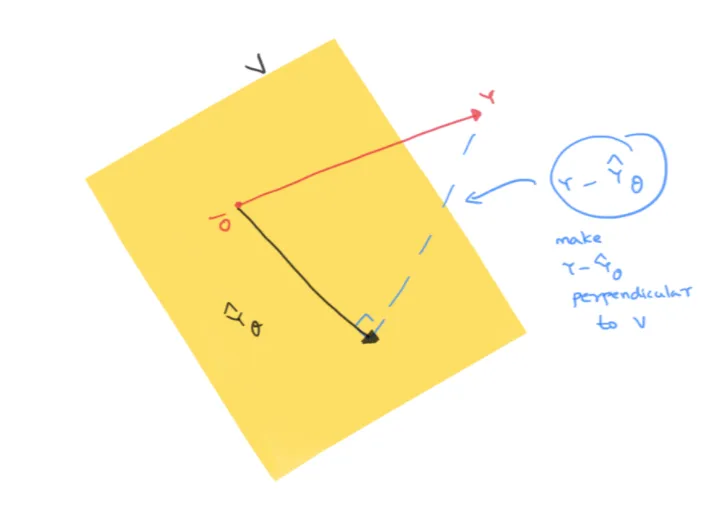
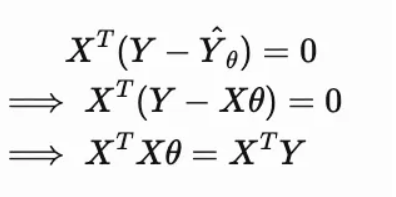
Assignment 1b

# Importing the libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error, r2_score

# Load dataset
data = pd.read_csv("data.csv")

train_data = data.sample(frac=0.75, random_state=1)
test_data = data.drop(train_data.index)

# linear regression model
regressor = LinearRegression() 
#To explicitly use SGD
regressor = SGDRegressor()

# fitting
regressor.fit(train_data[['x']], train_data['y'])

# predicting
y_pred = regressor.predict(test_data[['x']])

# Evaluate
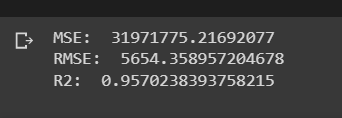
mse = mean_squared_error(test_data['y'], y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(test_data['y'], y_pred)

print("MSE: ", mse)
print("RMSE: ", rmse)
print("R2: ", r2)

Assignment 1b

Assignment 1b

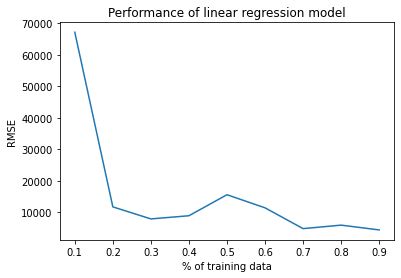
Draw a performance plot of the regression model(% of training data vs RMSE)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# function to calculate RMSE
def rmse(y_true, y_pred):
    return np.sqrt(np.mean((y_true - y_pred) ** 2))

  train_sizes = np.arange(0.1, 1.0, 0.1)

# To store rmse values
rmse_values = []

# Parse through the training data
for train_size in train_sizes:

    # perform linear regression on training size
    n = len(data)
    train_size = int(n * train_size)
    X_train, y_train = X[:train_size], y[:train_size]
    X_test, y_test = X[train_size:], y[train_size:]

    X_train_norm = (X_train - np.mean(X_train)) / np.std(X_train)
    y_train_norm = (y_train - np.mean(y_train)) / np.std(y_train)
    X_train_norm = np.c_[np.ones((len(X_train_norm), 1)), X_train_norm]
    optimised = np.linalg.inv(X_train_norm.T.dot(X_train_norm)).dot(X_train_norm.T).dot(y_train_norm)

    X_test_norm = (X_test - np.mean(X_train)) / np.std(X_train)
    X_test_norm = np.c_[np.ones((len(X_test_norm), 1)), X_test_norm]
    y_pred_norm = X_test_norm.dot(optimised)

    y_pred = y_pred_norm * np.std(y_train) + np.mean(y_train)

    rmse_values.append(rmse(y_test, y_pred))

# Plot 
plt.plot(train_sizes, rmse_values)
plt.xlabel('% of training data')
plt.ylabel('RMSE')
plt.title('Performance of linear regression model')
plt.show()

Assignment 1b

Draw a performance plot of the regression model(% of training data vs RMSE)

Assignment 1c

Logistic Regression

Assignment 1c

Logistic Regression

Assignment 1c

Logistic Regression

Σ\Sigma
\Sigma
∫\int
\int
y^\hat{y}
\hat{y}
x1x_1
x_1
w1w_1
w_1
x3x_3
x_3
x2x_2
x_2
w2w_2
w_2
w3w_3
w_3

Assignment 1c

Logistic Regression

Σ\Sigma
\Sigma
∫\int
\int
y^\hat{y}
\hat{y}
x1x_1
x_1
w1w_1
w_1
x3x_3
x_3
x2x_2
x_2
w2w_2
w_2
w3w_3
w_3

Assignment 1c

Logistic Regression

11
1
0.50.5
0.5
33
3
22
2
0.20.2
0.2
0.40.4
0.4
y^\hat{y}
\hat{y}
g(z)g(z)
g(z)
x=[123]y=1random weights , w=[0.50.20.4]x = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \\ y = 1 \\ \text{random weights , } \\ w = \begin{bmatrix} 0.5 \\ 0.2 \\ 0.4 \end{bmatrix} \\
x = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \\ y = 1 \\ \text{random weights , } \\ w = \begin{bmatrix} 0.5 \\ 0.2 \\ 0.4 \end{bmatrix} \\
z=wT⋅xz = w^T \cdot x
z = w^T \cdot x
[1⋅0.5+2⋅0.2+3⋅0.4][1 \cdot 0.5 + 2 \cdot 0.2 + 3 \cdot 0.4]
[1 \cdot 0.5 + 2 \cdot 0.2 + 3 \cdot 0.4]
z = 2.1\text{z = 2.1}
\text{z = 2.1}

Assignment 1c

Logistic Regression

Activation Function\text{Activation Function}
\text{Activation Function}

Sigmoid Function

g(z)=11+e−zg(z) = \frac{1}{1 + e^{-z} }
g(z) = \frac{1}{1 + e^{-z} }
g′(z)=g(z)⋅(1−g(z))g'(z) = g(z) \cdot (1 - g(z) )
g'(z) = g(z) \cdot (1 - g(z) )

Assignment 1c

Logistic Regression

g(z)=11+e−zg(z) = \frac{1}{1 + e^{-z} }
g(z) = \frac{1}{1 + e^{-z} }
11
1
0.50.5
0.5
33
3
22
2
0.20.2
0.2
0.40.4
0.4
g(z)g(z)
g(z)
z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909

Assignment 1c

Logistic Regression

g(z)=11+e−zg(z) = \frac{1}{1 + e^{-z} }
g(z) = \frac{1}{1 + e^{-z} }
11
1
0.50.5
0.5
33
3
22
2
0.20.2
0.2
0.40.4
0.4
g(z)g(z)
g(z)
z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909

OOPs! 🤥

Wasn't the true output 1?

We Should Punish the Network , so

It Behaves Properly

 

LOSS FUNCTIONS

Answer:

Assignment 1c

Logistic Regression

LOSS FUNCTIONS

Binary Cross Entropy Loss

L(y,y^)=−y⋅log(y^)−(1−y)⋅log(1−y^)L(y , \hat{y}) = - y \cdot log(\hat{y} ) - (1-y) \cdot log(1 - \hat{y})
L(y , \hat{y}) = - y \cdot log(\hat{y} ) - (1-y) \cdot log(1 - \hat{y})
L(y,y^)={−log(y^)y==1−log(1−y^)y==0L(y , \hat{y} ) = \begin{cases} - log(\hat{y}) && y == 1 \\ - log(1 - \hat{y}) && y == 0 \end{cases}
L(y , \hat{y} ) = \begin{cases} - log(\hat{y}) && y == 1 \\ - log(1 - \hat{y}) && y == 0 \end{cases}

Assignment 1c

Logistic Regression

w=w+(−1)⋅α(∂L(y,y^)∂w)w = w + (-1) \cdot \alpha (\frac{\partial L(y,\hat{y} )}{\partial w})
w = w + (-1) \cdot \alpha (\frac{\partial L(y,\hat{y} )}{\partial w})
α→scalar→Learning Rate\alpha \rightarrow scalar \rightarrow Learning \, Rate
\alpha \rightarrow scalar \rightarrow Learning \, Rate

Assignment 1c

Logistic Regression

Assignment 1c

Logistic Regression

11
1
0.50.5
0.5
33
3
22
2
0.20.2
0.2
0.40.4
0.4
g(z)g(z)
g(z)
z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909
L(1,0.8009)=−1⋅log(0.8909)−(1−1)⋅log(1−0.8909)L(1 , 0.8009) = - 1 \cdot log(0.8909) - (1-1) \cdot log(1 - 0.8909)
L(1 , 0.8009) = - 1 \cdot log(0.8909) - (1-1) \cdot log(1 - 0.8909)

Assignment 1c

Logistic Regression

11
1
0.50.5
0.5
33
3
22
2
0.20.2
0.2
0.40.4
0.4
g(z)g(z)
g(z)
z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909
L(1,0.8009)=0.1155L(1 , 0.8009) = 0.1155
L(1 , 0.8009) = 0.1155

Assignment 1c

Logistic Regression

11
1
0.50.5
0.5
33
3
22
2
0.20.2
0.2
0.40.4
0.4
z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909
L(1,0.8009)=0.1155L(1 , 0.8009) = 0.1155
L(1 , 0.8009) = 0.1155
∂L∂y^\frac{\partial L}{\partial \hat{y} }
\frac{\partial L}{\partial \hat{y} }
∂L∂y^=−yy^+1−y1−y^\frac{\partial L}{\partial \hat{y}} = \frac{-y}{\hat{y}} + \frac{1 - y}{1 - \hat{y}}
\frac{\partial L}{\partial \hat{y}} = \frac{-y}{\hat{y}} + \frac{1 - y}{1 - \hat{y}}
∂L(1,0.8909)∂y^=−10.89=−1.123\frac{ \partial L(1 , 0.8909) }{ \partial \hat{y}}= - \frac{1}{0.89} = -1.123
\frac{ \partial L(1 , 0.8909) }{ \partial \hat{y}}= - \frac{1}{0.89} = -1.123
zz
z
g(z)g(z)
g(z)

Assignment 1c

Logistic Regression

11
1
0.50.5
0.5
33
3
22
2
0.20.2
0.2
0.40.4
0.4
z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909
L(1,0.8009)=0.1155L(1 , 0.8009) = 0.1155
L(1 , 0.8009) = 0.1155
∂L∂y^=−1.123\frac{\partial L}{\partial \hat{y} }=-1.123
\frac{\partial L}{\partial \hat{y} }=-1.123
zz
z
g(z)g(z)
g(z)
∂L∂z\frac{\partial L}{\partial z }
\frac{\partial L}{\partial z }
∂L∂z=∂L∂y^⋅∂y^∂z\frac{ \partial L} {\partial z} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z}
\frac{ \partial L} {\partial z} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z}
(−1y^)⋅(y^(1−y^))\left( -\frac{1} {\hat{y}} \right) \cdot \left( \hat{y} (1 - \hat{y}) \right)
\left( -\frac{1} {\hat{y}} \right) \cdot \left( \hat{y} (1 - \hat{y}) \right)
−1.123⋅(0.8909(1−0.8909))=−0.1092-1.123 \cdot (0.8909(1-0.8909)) \\ = -0.1092
-1.123 \cdot (0.8909(1-0.8909)) \\ = -0.1092

Assignment 1c

Logistic Regression

11
1
33
3
22
2
z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909
L(1,0.8009)=0.1155L(1 , 0.8009) = 0.1155
L(1 , 0.8009) = 0.1155
∂L∂y^=−1.123\frac{\partial L}{\partial \hat{y} }=-1.123
\frac{\partial L}{\partial \hat{y} }=-1.123
zz
z
g(z)g(z)
g(z)
∂L∂z=−0.1092\frac{\partial L}{\partial z } = -0.1092
\frac{\partial L}{\partial z } = -0.1092
∂L∂wi=∂L∂z⋅∂z∂wi\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial w_i}
\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial w_i}
∂z∂wi=∂∑wixi∂wi=xi\frac{\partial z}{\partial w_i} =\frac{\partial \sum w_i x_i}{\partial w_i} = x_i
\frac{\partial z}{\partial w_i} =\frac{\partial \sum w_i x_i}{\partial w_i} = x_i
∂L∂w1=−0.1092∗1\frac{\partial L}{\partial w_1} = -0.1092*1 \\
\frac{\partial L}{\partial w_1} = -0.1092*1 \\
∂L∂w2=−0.1092∗2\frac{\partial L}{\partial w_2} = -0.1092*2 \\
\frac{\partial L}{\partial w_2} = -0.1092*2 \\
∂L∂w3=−0.1092∗3\frac{\partial L}{\partial w_3} = -0.1092*3 \\
\frac{\partial L}{\partial w_3} = -0.1092*3 \\
∂L∂w1\frac{\partial L}{\partial w_1}
\frac{\partial L}{\partial w_1}
∂L∂w3\frac{\partial L}{\partial w_3}
\frac{\partial L}{\partial w_3}
∂L∂w2\frac{\partial L}{\partial w_2}
\frac{\partial L}{\partial w_2}

Assignment 1c

Logistic Regression

z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909
L(1,0.8009)=0.1155L(1 , 0.8009) = 0.1155
L(1 , 0.8009) = 0.1155
∂L∂y^=−1.123\frac{\partial L}{\partial \hat{y} }=-1.123
\frac{\partial L}{\partial \hat{y} }=-1.123
∂L∂z=−0.1092\frac{\partial L}{\partial z } = -0.1092
\frac{\partial L}{\partial z } = -0.1092
∂L∂w1=−0.1092\frac{\partial L}{\partial w_1} = -0.1092 \\
\frac{\partial L}{\partial w_1} = -0.1092 \\
∂L∂w2=−0.2184\frac{\partial L}{\partial w_2} = -0.2184 \\
\frac{\partial L}{\partial w_2} = -0.2184 \\
∂L∂w3=−0.3276\frac{\partial L}{\partial w_3} = -0.3276 \\
\frac{\partial L}{\partial w_3} = -0.3276 \\
w1=w1−α⋅∂L∂w1w_1 = w_1 - \alpha \cdot \frac{\partial L}{\partial w_1}
w_1 = w_1 - \alpha \cdot \frac{\partial L}{\partial w_1}
w2=w2−α⋅∂L∂w2w_2 = w_2 - \alpha \cdot \frac{\partial L}{\partial w_2}
w_2 = w_2 - \alpha \cdot \frac{\partial L}{\partial w_2}
w3=w3−α⋅∂L∂w3w_3 = w_3 - \alpha \cdot \frac{\partial L}{\partial w_3}
w_3 = w_3 - \alpha \cdot \frac{\partial L}{\partial w_3}
α→Learning rate\alpha \rightarrow Learning \ rate
\alpha \rightarrow Learning \ rate

Assignment 1c

Logistic Regression

z = 2.1\text{z = 2.1}
\text{z = 2.1}
y^=0.8909\hat{y} = 0.8909
\hat{y} = 0.8909
L(1,0.8009)=0.1155L(1 , 0.8009) = 0.1155
L(1 , 0.8009) = 0.1155
∂L∂y^=−1.123\frac{\partial L}{\partial \hat{y} }=-1.123
\frac{\partial L}{\partial \hat{y} }=-1.123
∂L∂z=−0.1092\frac{\partial L}{\partial z } = -0.1092
\frac{\partial L}{\partial z } = -0.1092
∂L∂w1=−0.1092\frac{\partial L}{\partial w_1} = -0.1092 \\
\frac{\partial L}{\partial w_1} = -0.1092 \\
∂L∂w2=−0.2184\frac{\partial L}{\partial w_2} = -0.2184 \\
\frac{\partial L}{\partial w_2} = -0.2184 \\
∂L∂w3=−0.3276\frac{\partial L}{\partial w_3} = -0.3276 \\
\frac{\partial L}{\partial w_3} = -0.3276 \\
α→Learning rate\alpha \rightarrow Learning \ rate
\alpha \rightarrow Learning \ rate
w1=0.5−1⋅(−0.1092)w_1 = 0.5 - 1 \cdot (-0.1092)
w_1 = 0.5 - 1 \cdot (-0.1092)
w2=0.2−1⋅(−0.2184)w_2 = 0.2- 1 \cdot (-0.2184)
w_2 = 0.2- 1 \cdot (-0.2184)
w3=0.4−1⋅(−0.3276)w_3 = 0.4- 1 \cdot (-0.3276)
w_3 = 0.4- 1 \cdot (-0.3276)

Assignment 1c

Logistic Regression

x=[123]y=1updated weights , w=[0.60920.41840.7276]x = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \\ y = 1 \\ \text{updated weights , } \\ w = \begin{bmatrix} 0.6092 \\ 0.4184 \\ 0.7276 \end{bmatrix} \\
x = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \\ y = 1 \\ \text{updated weights , } \\ w = \begin{bmatrix} 0.6092 \\ 0.4184 \\ 0.7276 \end{bmatrix} \\
11
1
0.60920.6092
0.6092
33
3
22
2
0.41840.4184
0.4184
0.72760.7276
0.7276
y^\hat{y}
\hat{y}
g(z)g(z)
g(z)
z=wT⋅xz = w^T \cdot x
z = w^T \cdot x
[1⋅0.6092+2⋅0.4184+3⋅0.7276]=3.6288[1 \cdot 0.6092 + 2 \cdot 0.4184 + 3 \cdot 0.7276] \\ = 3.6288
[1 \cdot 0.6092 + 2 \cdot 0.4184 + 3 \cdot 0.7276] \\ = 3.6288
g(z)=g(3.6288)=0.9739g(z) = g(3.6288) = 0.9739
g(z) = g(3.6288) = 0.9739
L(1,0.9739)=0.02L(1, 0.9739) = 0.02
L(1, 0.9739) = 0.02
Old loss=0.1155Old \ loss = 0.1155
Old \ loss = 0.1155

Assignment 1c

Single, Binary Logistic Regression Using Inbuilt command

data = load_breast_cancer()
X = data.data[:, 0].reshape(-1, 1)  # Using only the first feature
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
print(classification_report(y_test, y_pred))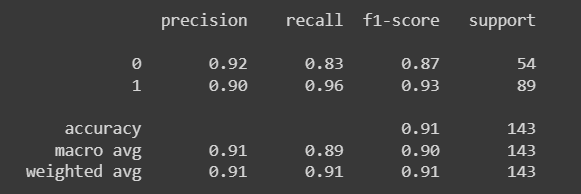

Assignment 1c

Single, Binary Logistic Regression Using Inbuilt command

data = load_breast_cancer()
X = data.data[:, 0].reshape(-1, 1)  # Using only the first feature
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
print(classification_report(y_test, y_pred))

Assignment 1c

Single, Binary Logistic Regression 

class Logistic_Regression:
    def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
        self.lr = lr
        self.num_iter = num_iter
        self.fit_intercept = fit_intercept
        self.verbose = verbose
        
    def __add_intercept(self, X):
        intercept = np.ones((X.shape[0], 1))
        return np.concatenate((intercept, X), axis=1)
    
    def __compute_cost(self, h, y):
        epsilon = 1e-5
        m = y.shape[0]
        cost = (-1/m) * np.sum(y*np.log(h+epsilon) + (1-y)*np.log(1-h+epsilon))
        return cost
    
    def fit(self, X, y):
        if self.fit_intercept:
            X = self.__add_intercept(X)
        
        self.theta = np.zeros(X.shape[1])
        
        for i in range(self.num_iter):
            z = np.dot(X, self.theta)
            h = sigmoid(z)
            gradient = np.dot(X.T, (h-y)) / y.size
            self.theta -= self.lr * gradient
            
            if self.verbose and i % 10000 == 0:
                z = np.dot(X, self.theta)
                h = sigmoid(z)
                print(f'loss: {self.__compute_cost(h, y)} \t')
                
    def predict_prob(self, X):
        if self.fit_intercept:
            X = self.__add_intercept(X)
            
        return sigmoid(np.dot(X, self.theta))
    
    def predict(self, X, threshold=0.5):
        return self.predict_prob(X) >= threshold

Assignment 1c

Single, Binary Logistic Regression 

model = Logistic_Regression(lr=0.1, num_iter=300000)
model.fit(X_train, y_train.values.ravel())

preds = model.predict(X_test)
print(classification_report(y_test, preds))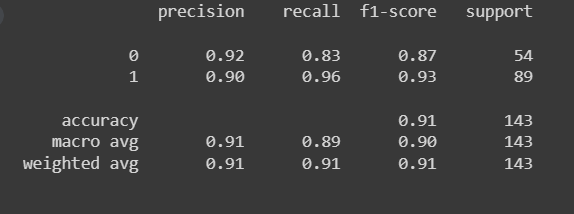

Assignment 1d

Random Forest and Decision Trees

Classification Data

Given these information , predict if the person may get diabetes in the future

Regression Data

Given the information , predict the humidity for a given day

Evaluating Classifiers

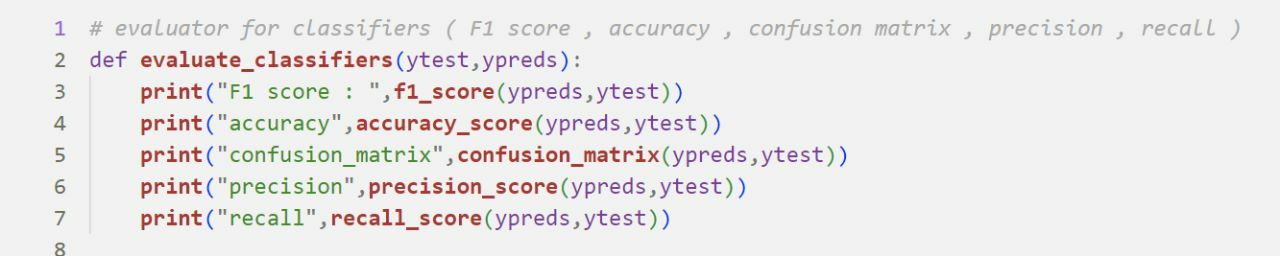
Evaluating Regressors

Performance plots

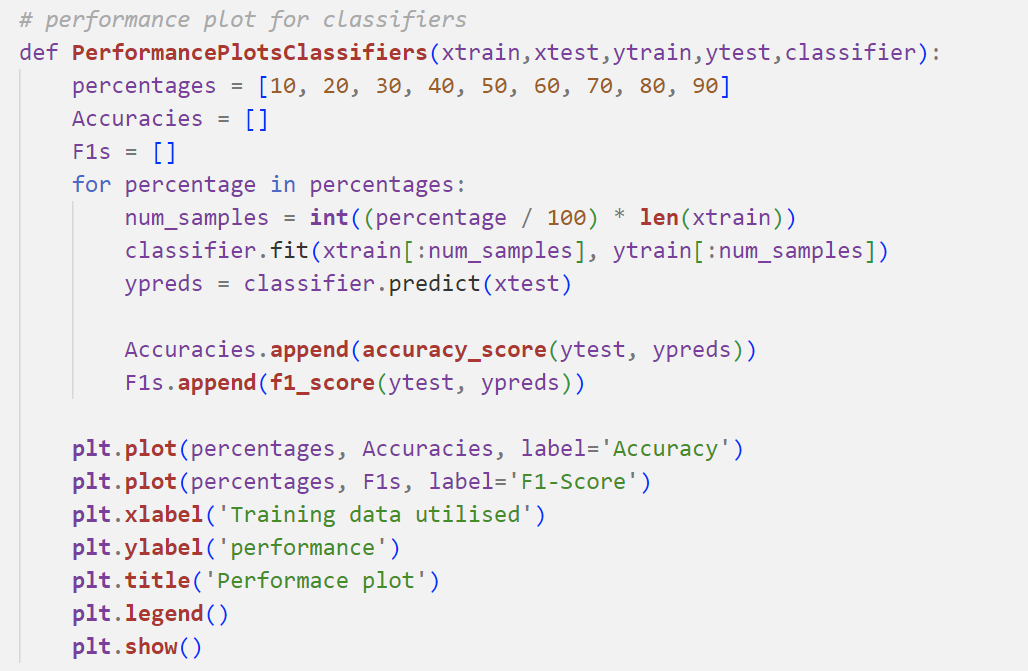
Performance plots

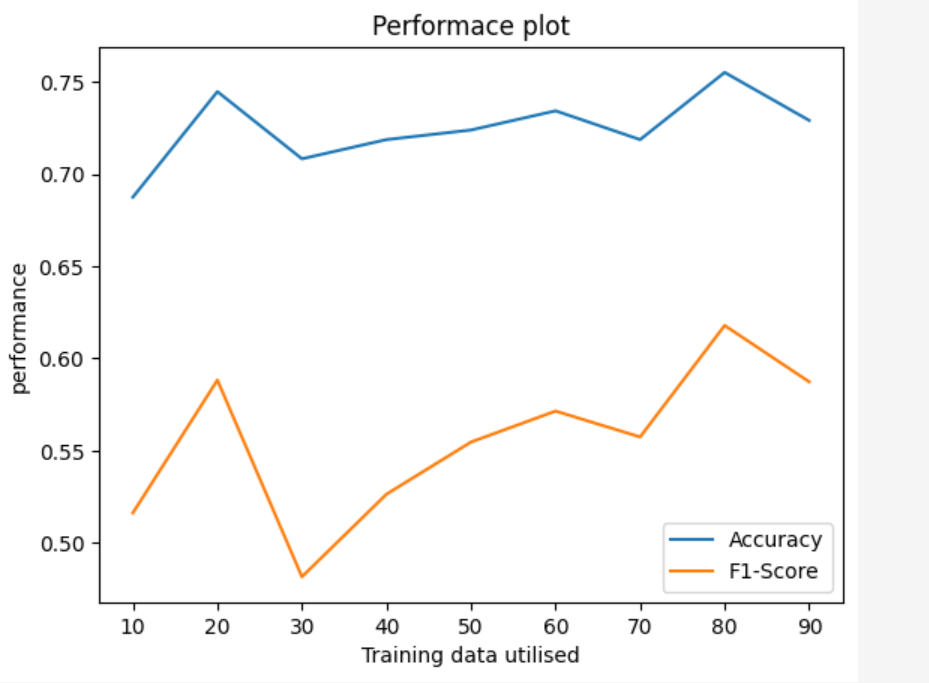
Random Forest Classifier

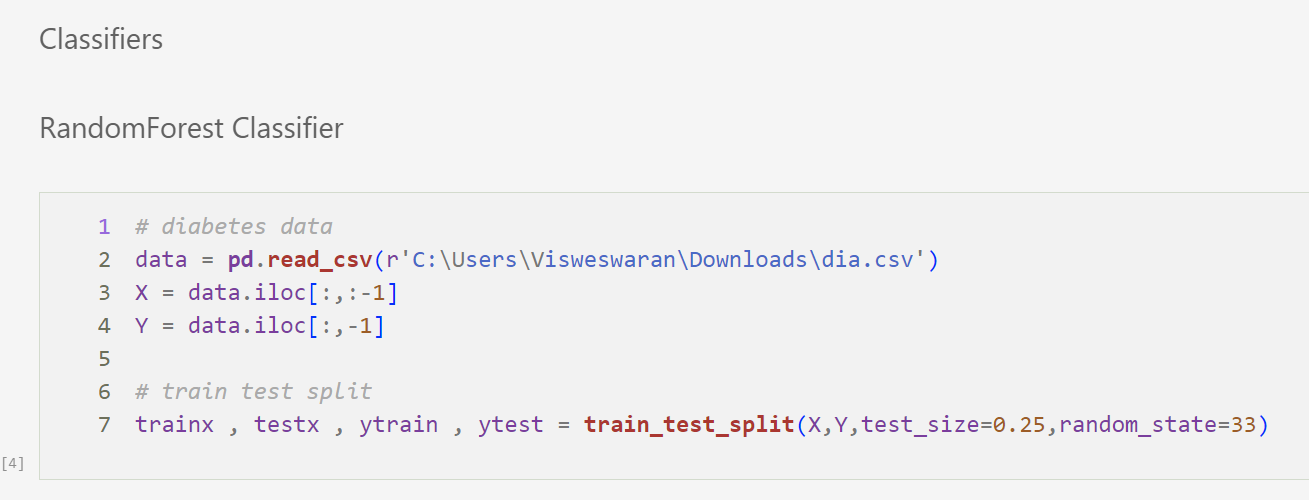
Random Forest Classifier

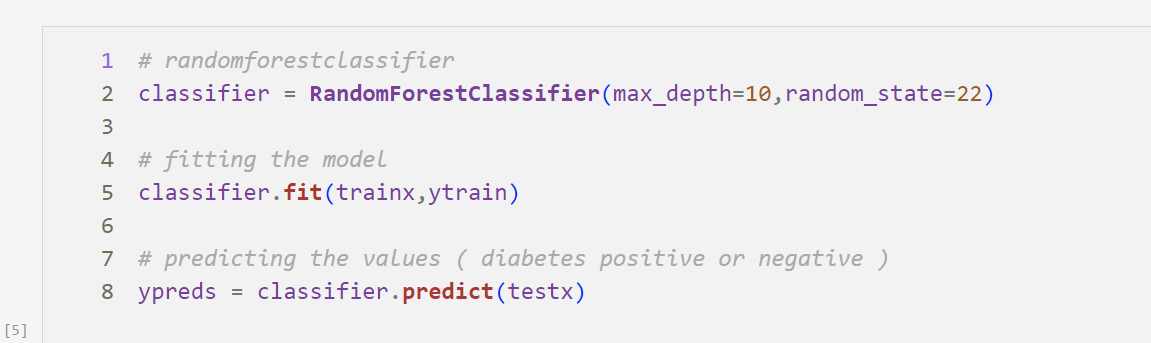
Random Forest Classifier

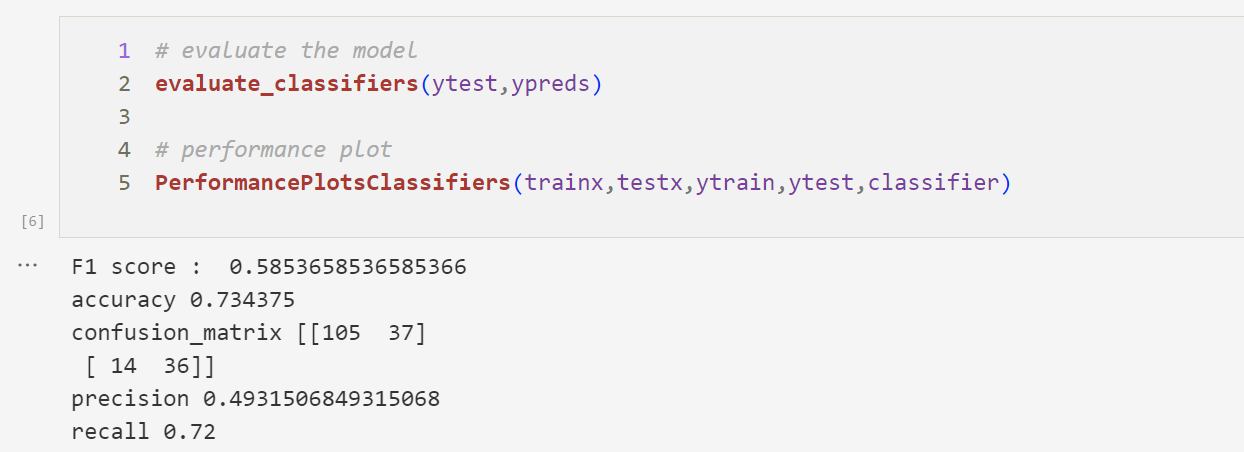
Random Forest Classifier Performance Plot

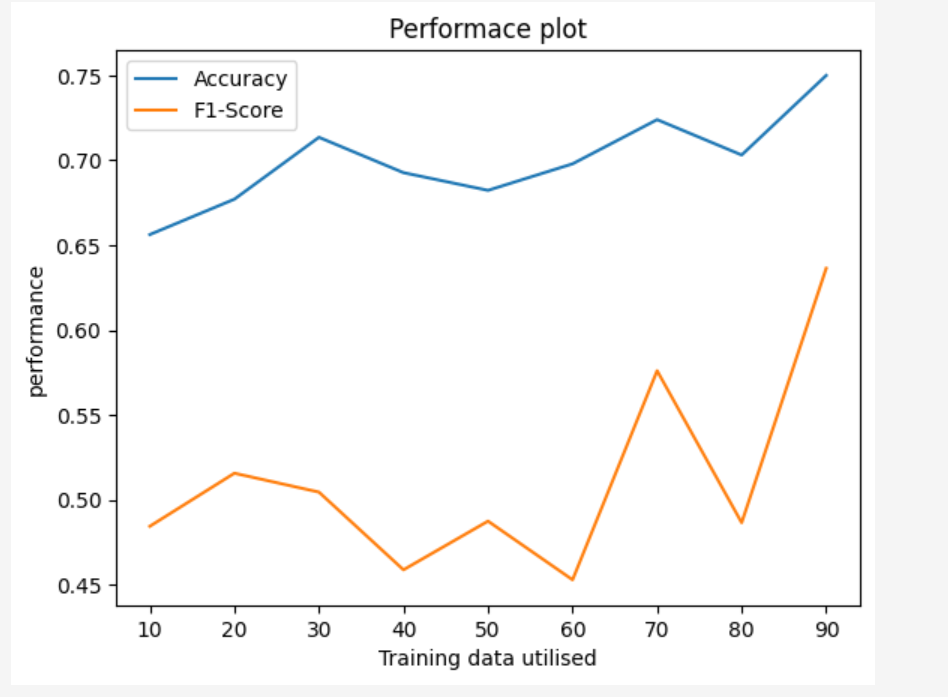
Decision Tree Classifier 

Decision Tree Classifier 

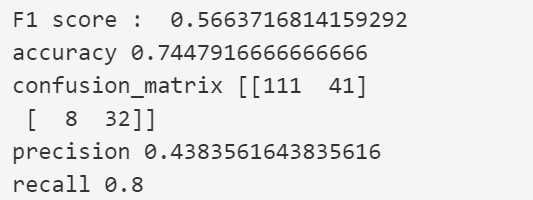
Decision Tree Classifier Performance PLot

Random Forest Regression

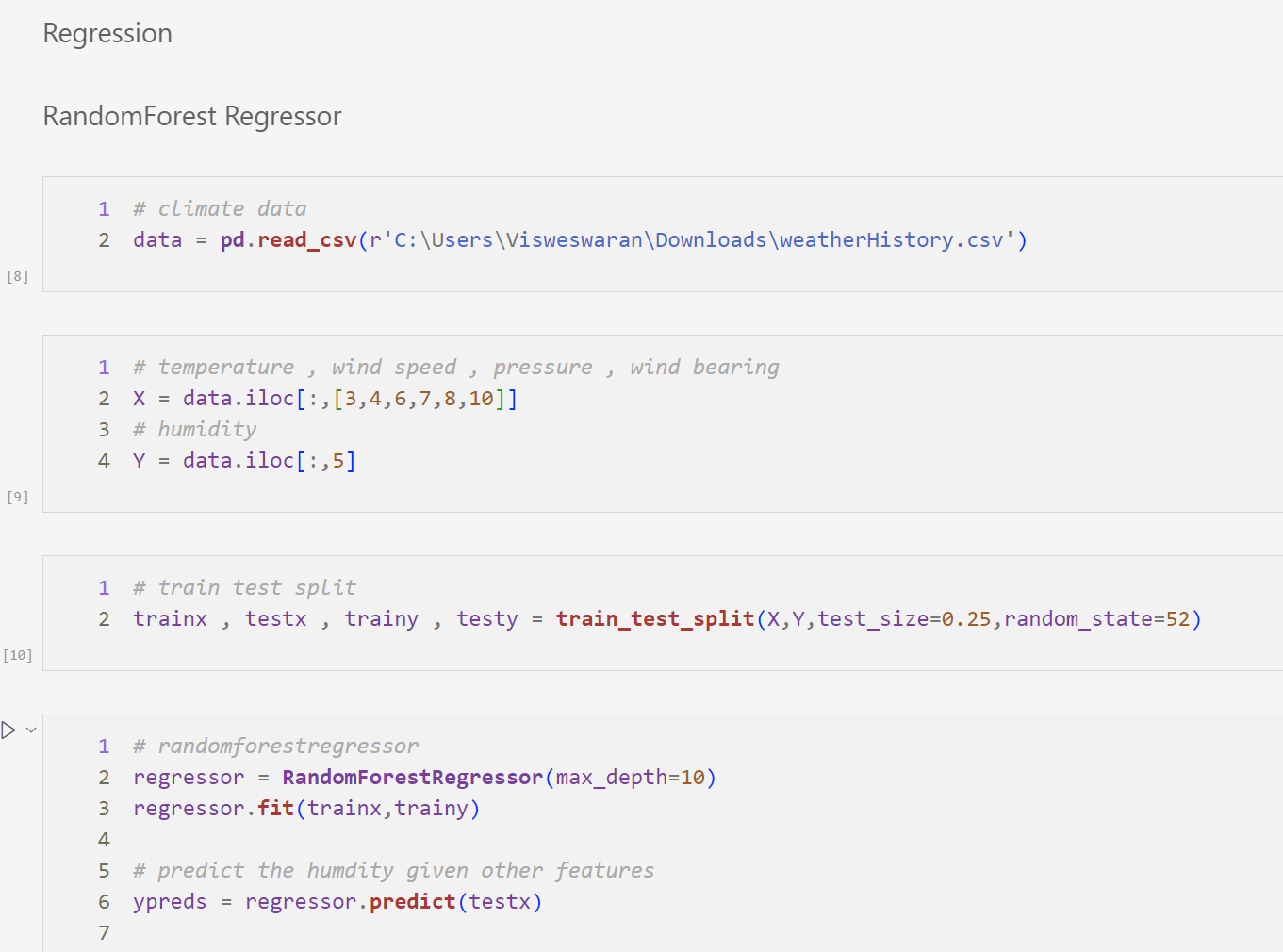
Random Forest Regression

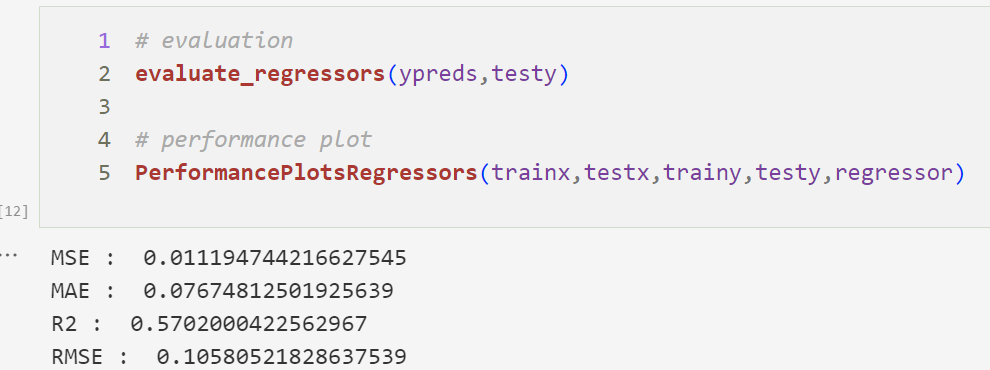
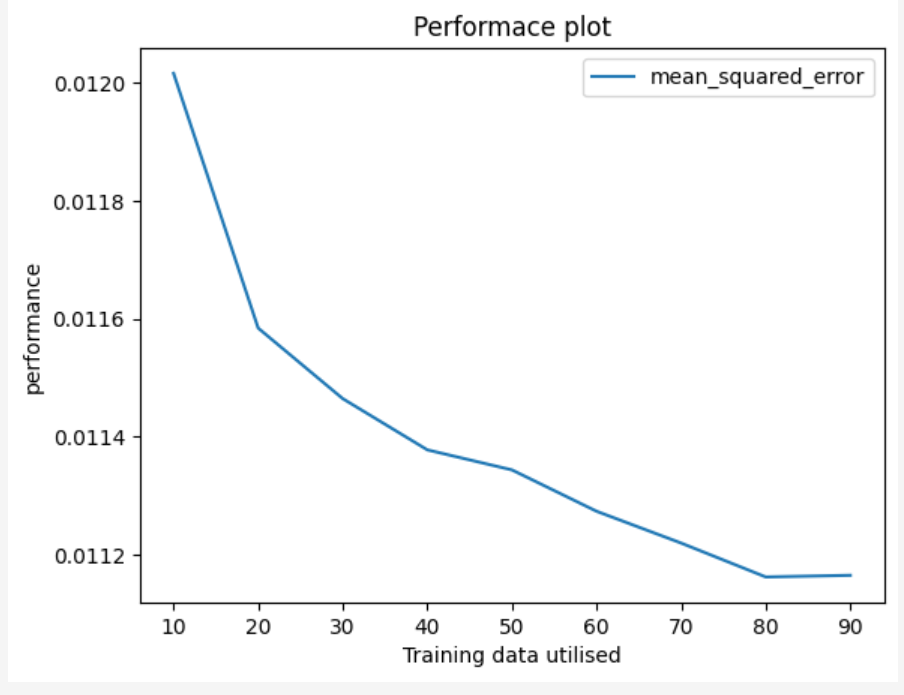
Random Forest Regression Performance Plot

Decision Tree Regression 

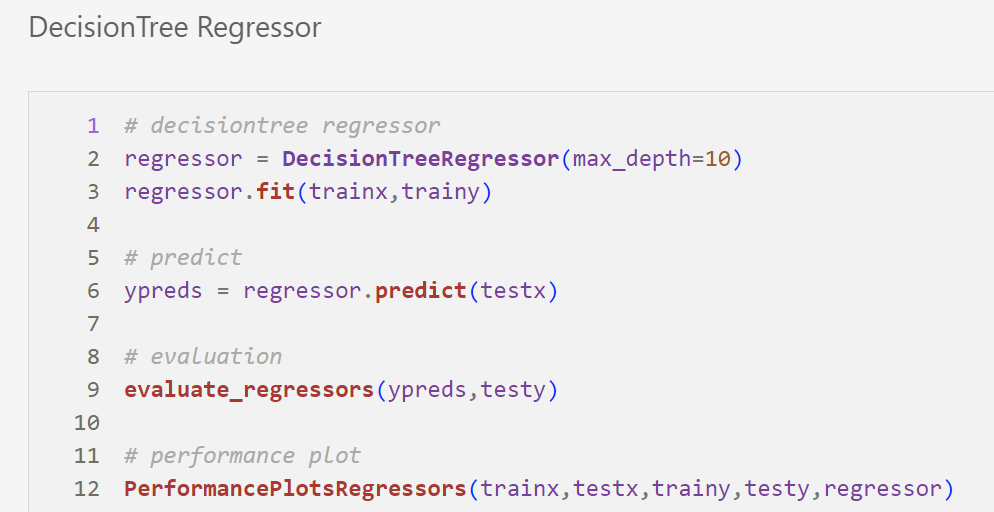
Decision Tree Regression 

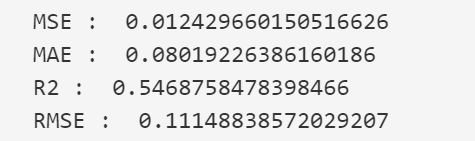
Decision Tree Regression Performance Plot

deck

By Incredeble us

Made with Slides.com

deck

  • 91

More from Incredeble us