21AIE212
RNA Secondary Structure using Dynamic Programming
Design and Analysis of Algortihms
21AIE212
Anirudh Edpuganti - CB.EN.U4AIE20005
Onteddu Chaitanya Reddy - CB.EN.U4AIE20045
Pillalamarri Akshaya - CB.EN.U4AIE20049
Pingali Sathvika - CB.EN.U4AIE20050
Team-2
RNA Secondary Structure using Dynamic Programming
21AIE212
Contents
Contents
- RNA Secondary Structure
Contents
- RNA Secondary Structure
- Conditions
Contents
- RNA Secondary Structure
- Conditions
- Formulation
Contents
- RNA Secondary Structure
- Conditions
- Formulation
- Implementation
Contents
- RNA Secondary Structure
- Conditions
- Formulation
- Implementation
- Time Complexity
21AIE212
RNA Secondary Structure
21AIE212
Before that
Double-Stranded DNA
21AIE212
Before that
Double-Stranded DNA
Complimentary Base-Pairing
21AIE212
Double-Stranded DNA
Complimentary Base-Pairing
21AIE212
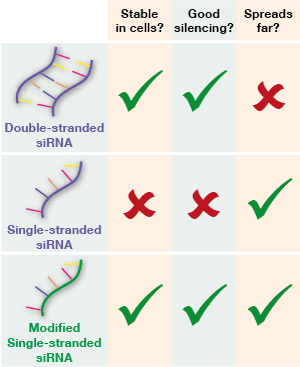
Double-Stranded DNA
Complimentary Base-Pairing
A
T
C
G
21AIE212
Single-Stranded RNA
21AIE212
Single-Stranded RNA
Second strand
21AIE212
Single-Stranded RNA
Second strand
Base Pairing ???
21AIE212
Single-Stranded RNA
Second strand
Base Pairing
Itself
21AIE212
Single-Stranded RNA
Second strand
Base Pairing
Itself
Formation of RNA Secondary Structure
21AIE212
RNA Secondary Structure
RNA Secondary Structure
Let us consider a sample RNA sequence
RNA Secondary Structure
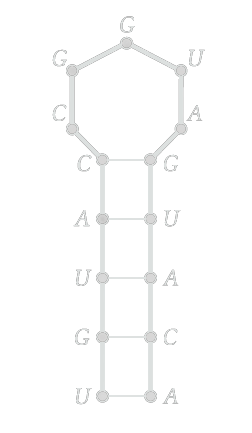
RNA = ACAUGAUGGCCAUGU
Now our sequence folds as
21AIE212
Conditions
Conditions
Conditions
Conditions
Now we can assume our sequence to be a set of pairs
Conditions
No sharp turns
Conditions
No sharp turns
Conditions
Complementary Base-pairs
Conditions
Complementary Base pairs
A
U
C
G
Conditions
Single Pair
Conditions
Single Pair
Conditions
Non Crossing Condition
Conditions
Non Crossing Condition
Conditions
What is the problem ?
Conditions
What is the problem ?
Molecule stability
Conditions
What is the problem ?
Molecule stability
# of base pairs
Conditions
What is the problem ?
# of base pairs
Conditions
What is the problem ?
Algorithm
Conditions
What is the problem ?
Algorithm
B
Input
Conditions
What is the problem ?
Algorithm
B
Input
Max. # base pairs
Output
21AIE212
Formulation
Formulation
Formulation
Formulation
Recall
Condition 1
Formulation
No-sharp turns
Formulation
Formulation
Final Solution
Formulation
Final Solution
Formulation
Try for a recurrence
Formulation
Subproblems
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
1 variable
Formulation
2 variables
1 variable
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Formulation
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)Formulation
Text
Attempt for another formulation
Formulation
Text
Attempt for another formulation
Formulation
Text
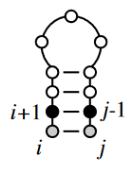
i,j pair
Formulation
Text

i,j pair
Formulation
Text

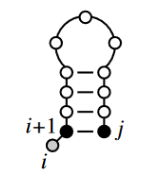
i unpaired
Formulation
Text


i unpaired
Formulation
Text


j unpaired
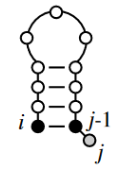
Formulation
Text


j unpaired

Formulation
Text


non crossing condition

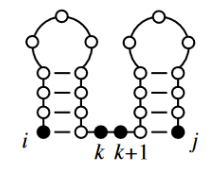
Formulation
Text


non crossing condition


Formulation
Text




Formulation
Text




Formulation
Text




Formulation
Text
Formulation
Text
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)21AIE212
Time Complexity
Time Complexity
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)Time Complexity
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)n
Time Complexity
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)n
n
Time Complexity
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)n
n
n
Time Complexity
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)n
n
n
O( )
Time Complexity
Initialize OPT(i,j) = 0 whenever i >= j-4
for k = 5,6,..,n-1
for i = 1,2,...,n-k
Set j = i + k
Compute OPT(i,j)
end
end
Return OPT(1,n)21AIE212
Implementation
Implementation
1st Approach
''' The function find_index takes in the matrix
and returns us the index corresponding to i and j
if i or j is not found in the matrix then it returns
the index of last row and 1st column element which
corresponds to zero'''
def find_index(opt,i,j):
if i==0 or j==0:
return np.shape(opt)[0]-1,0
else:
i_ = np.argwhere(opt[:,0]==i)
j_ = np.argwhere(opt[np.shape(opt)[0]-1,:]==j)
try:
return i_[0][0],j_[0][0]
except IndexError:
return np.shape(opt)[0]-1,0Implementation
def RNA(sequence):
n = len(sequence)
if n%2 == 0:
opt = np.zeros((int((n/2)+1),int(((n/2)+1))))
else:
opt = np.zeros((int((n-1)/2)+1,int((n-1)/2)+1))
opt[0,0] = np.shape(opt)[0] - 1
opt[np.shape(opt)[0]-1,1] = np.shape(opt)[1] + 1
for a in range(1,np.shape(opt)[0]):
opt[a,0] = opt[a-1,0] - 1
for b in range(2,np.shape(opt)[1]):
opt[np.shape(opt)[0]-1,b] = opt[np.shape(opt)[0]-1,b-1] + 1
for k in range(5,n):
for i in range(1,n-k+1):
j = i + k
second = [1+opt[find_index(opt,i,t-1)]+opt[find_index(opt,t+1,j-1)] for t in range(i,j-4)]
second_max = max(second,default=0)
if find_index(opt,i,j)==((np.shape(opt)[0]-1),0):
opt[find_index(opt,i,j)] = 0
else:
opt[find_index(opt,i,j)] = max(opt[find_index(opt,i,j-1)],second_max)
return opt[find_index(opt,1,n)]1st Approach
Implementation
def init_matrix(seq):
M = len(seq)
matrix = np.empty([M, M])
matrix[:] = np.NAN
matrix[range(M), range(M)] = 0
matrix[range(1, len(seq)), range(len(seq) - 1)] = 0
return matrix2nd Approach
Implementation
def Pair(pair):
pairs = {"A": "U", "U": "A", "G": "C", "C": "G"}
if pair in pairs.items():
return True
return False2nd Approach
Implementation
def fill(OPT, sequence):
"""
Fillint the matrix with the given conditions
"""
for k in range(1, len(sequence)):
for i in range(len(sequence) - k):
j = i + k
if j - i >= 4:
i_unpaired = OPT[i + 1][j] # i unpaired
j_unpaired = OPT[i][j - 1] # j unpaired
ij_pair = OPT[i + 1][j - 1] + Pair((sequence[i], sequence[j])) # i,j paired
non_crossing = max([OPT[i][t] + OPT[t + 1][j] for t in range(i, j)]) # non crossing condition
OPT[i][j] = max(i_unpaired , j_unpaired, ij_pair, non_crossing ) # max of all
else:
OPT[i][j] = 0
return OPT2nd Approach
Implementation
sequence = "ACAUGAUGGCCAUGU"
initial_matrix = init_matrix(sequence)
filled_matrix = fill(initial_matrix, sequence)
names = [_ for _ in sequence]
df = pd.DataFrame(filled_matrix, index = names, columns = names)
print(df)
print(f"Max # of base pairs : {filled_matrix[1,:][-1]}")2nd Approach
Implementation
Output
ACAUGAUGGCCAUGU
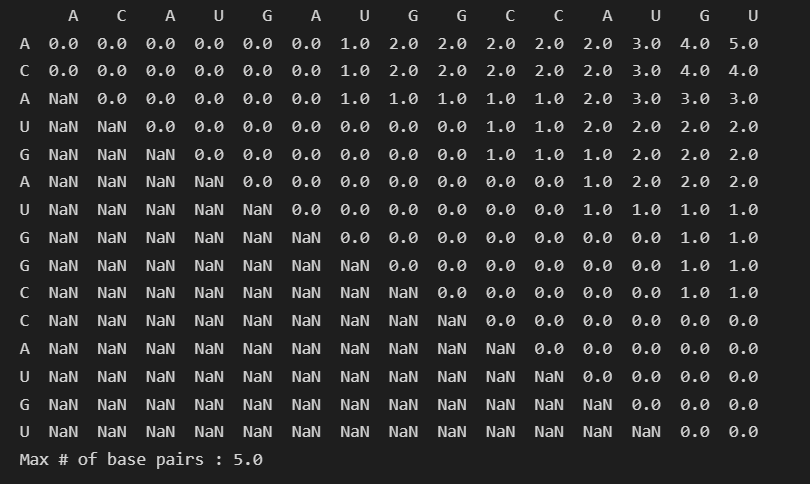
Implementation
Output
ACAUGAUGGCCAUGU


Implementation
Output
ACAUAAUGGCCAUGU
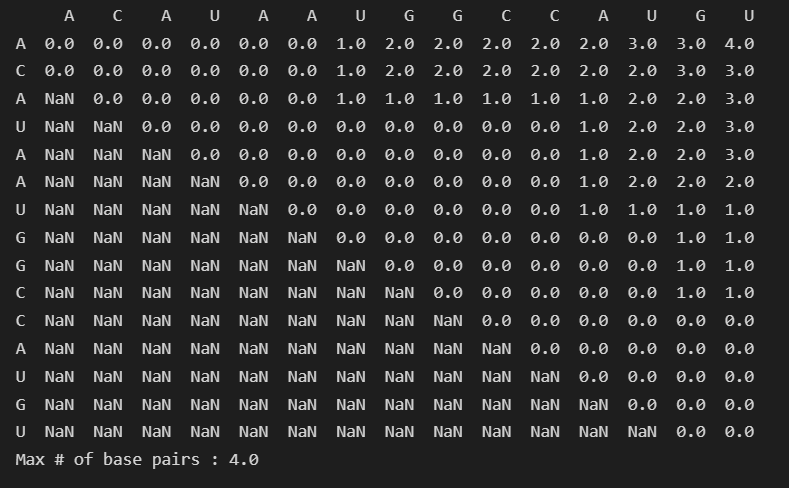
Implementation
Output
ACAUAAUGGCCAUGU


A
Thank you Sir
DAA
By Incredeble us
DAA
- 130



