Algorithms and Data structures
Lesson 1

$ whoami
Solution Architect
I like JS, React, movies, music and I'm a big fan of LOTR and Star Wars 🤓
May the Force be with you!
8 years with GlobalLogic
about 10 years in Web Development
Trusted Interviewer, speaker, and mentor at GlobalLogic
Part of the program committee at Fwdays

Inna Ivashchuk

Agenda:
- Introduction
- Is it necessary to learn Algorithms and Data structures?
- Complexity theory
-
Types of algorithms
-
Flowchart for algorithms representation
-
Collaborative Live-coding
Introduction

An algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output. An algorithm is thus a sequence of computational steps that transform the input into the output.

What is an algorithm?
„Software gets slower faster than hardware gets faster.“
Niklaus Virt

Start
Did you learn algorithms and data structures?
Time to learn 🤓
Congratulations 🥳
You are my hero
Resolved!
No
Yes
Let's check uses of Algorithms and Data structures

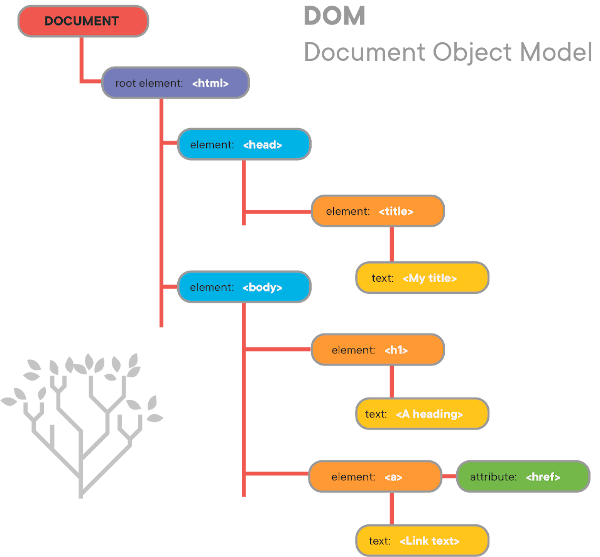
DOM: Tree
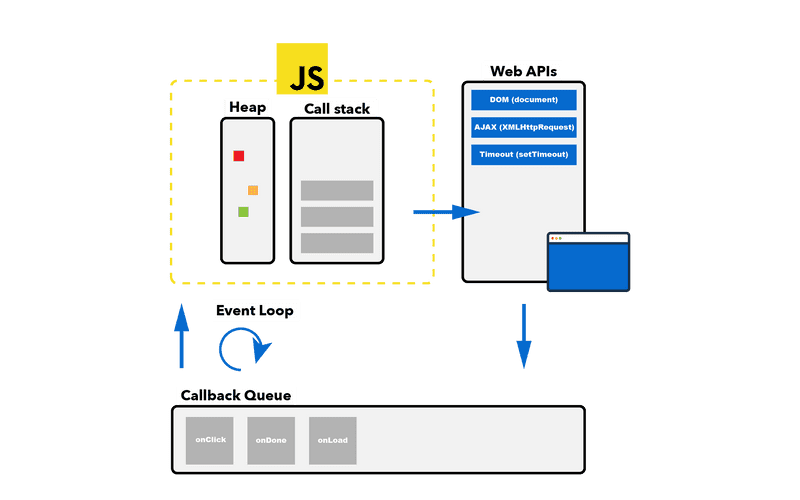
JS Event Loop: Heap, Queue, Stack
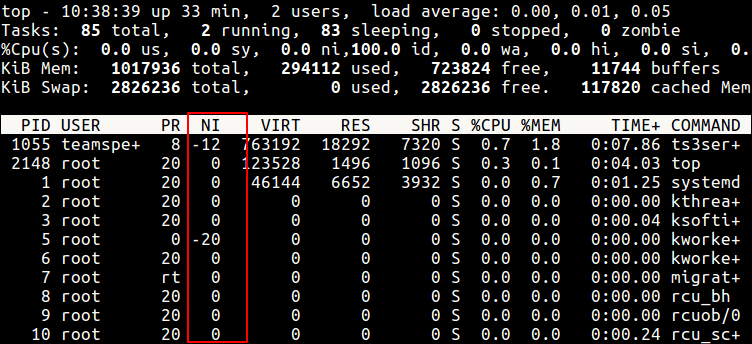
OS process priority: Heap & Priority Queue
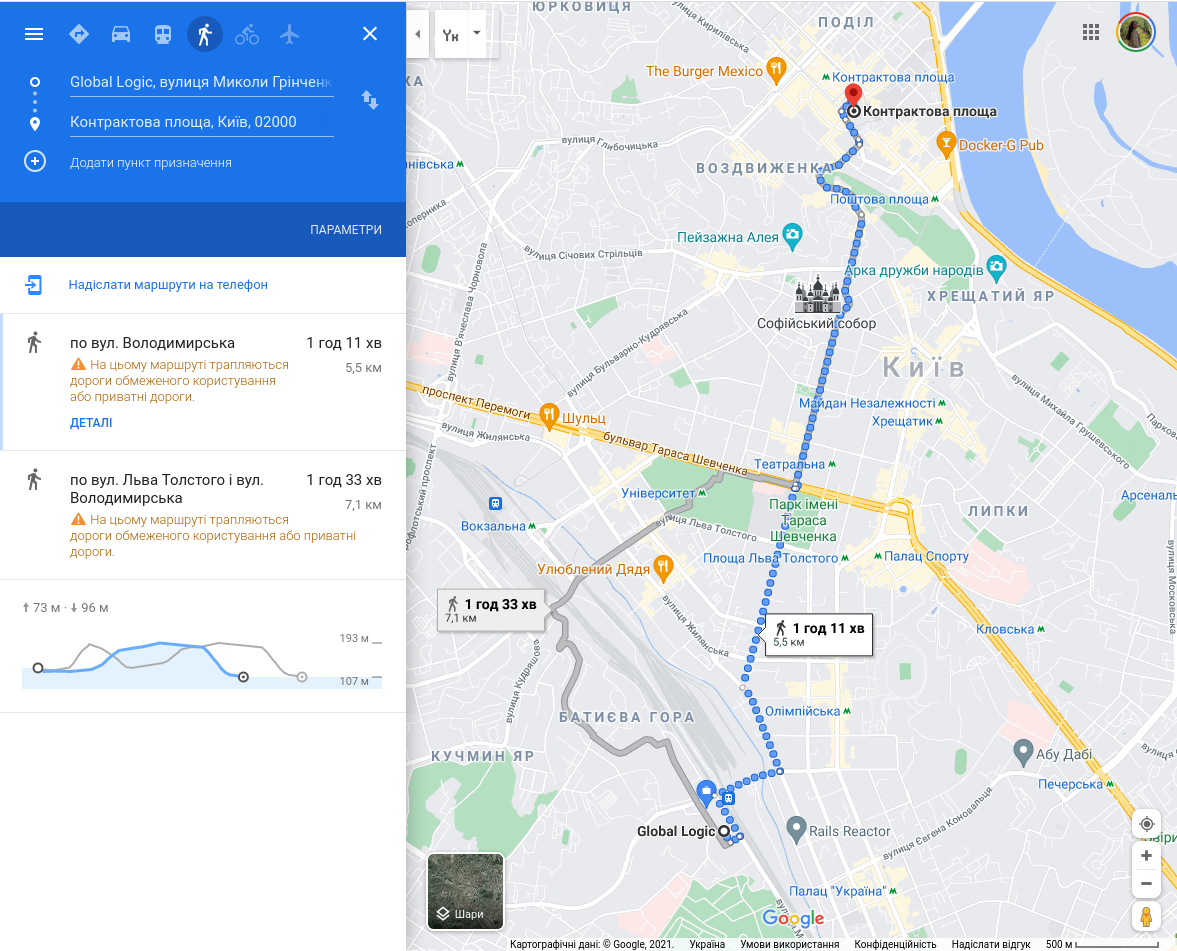
Google Maps: Dijkstra algorithm and Weighted Graph
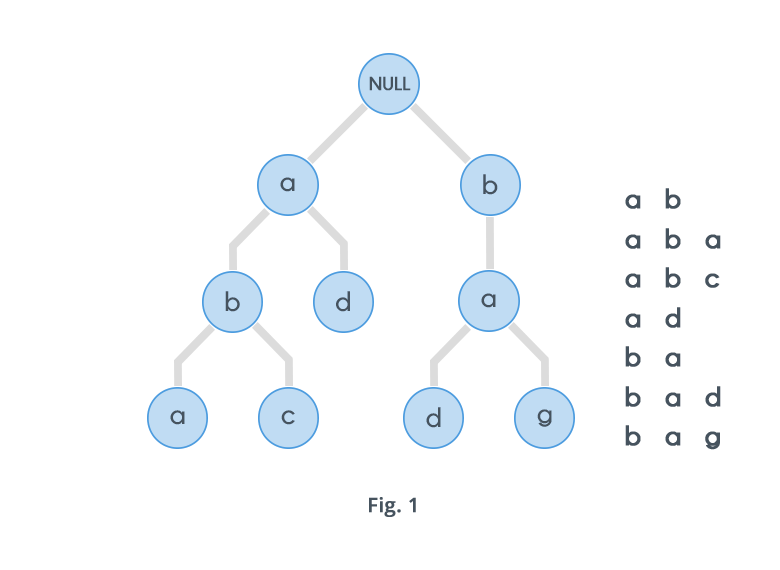
Google Search: Trie
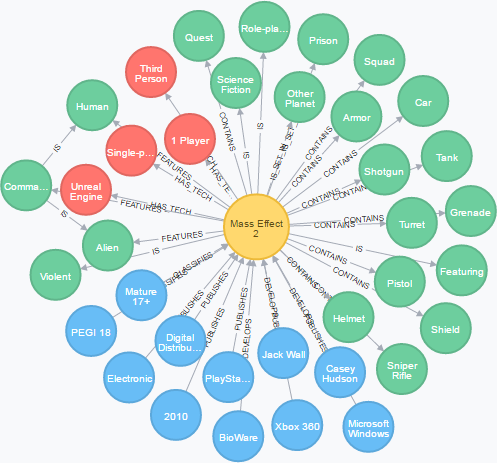
Recommendation system/engine: Graph










....and so many others
Is it necessary to learn Algorithms and Data structures?


"This is your chance to start learning Algorithms.
But after this, there is no turning back"
Yes?
No?
"Remember... All I'm offering is the truth, nothing more"
"Yes", if you would like to
become a true Software Engineer
pass interviews in the best companies in the world
create quality (productive and reliable) products
be able to solve really difficult problems
receive significantly more than the market average
Resources to train

"No", if you prefer to
make simple websites
don't understand the meaning of LinkedList, Heap, Stack and etc.
work on simple tasks
create a not complicated web servers (CRUD)
don't care about code quality and productivity
Complexity theory

Algorithm complexity
Big O notation, O
Omega notation, Ω
Theta notation, Θ
asymptotic notation, asymptotic complexity
O(n), O(log n), O(n * logn)
logarithmic polynomial
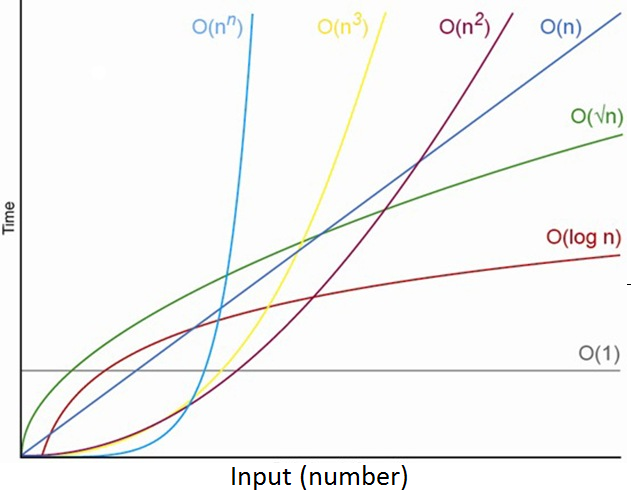

Don't be afraid
The complexity of an algorithm is a measure of the amount of time and/or space (memory) required by an algorithm for an input of a given size (n).
...it's just

Let's train on some JavaScript examples

and the first example
// Find sum of all numbers in array
function sumNumbersInArray(arr) {
let result = 0;
for (let i=0; i < arr.length; i++) {
result += arr[i];
}
return result;
}
// Test 1
sumNumbersInArray([1,2,3]);
// Test 2
sumNumbersInArray([1,2,3,4,5,6,7,8,9,10]);
Big O notation, O
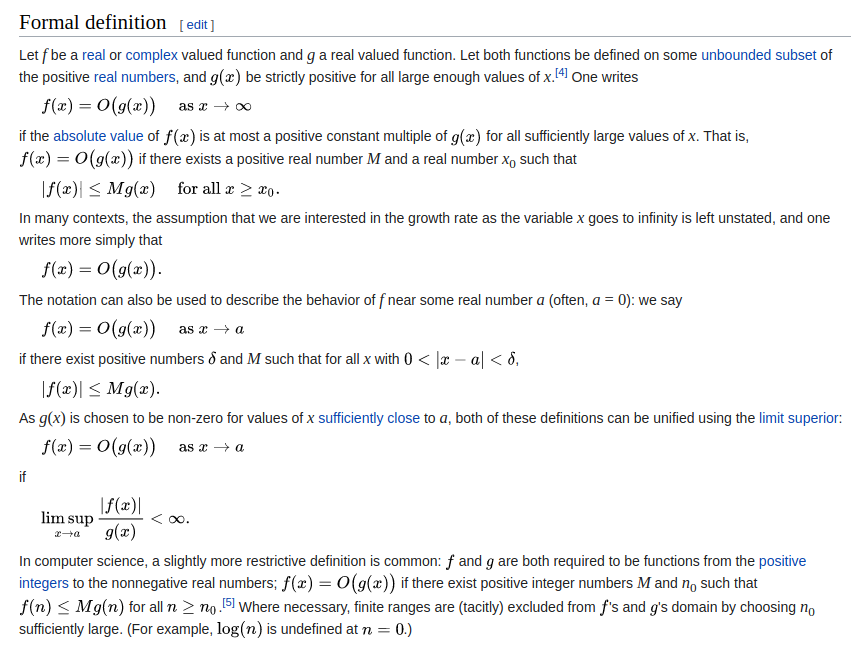

Big O notation, O
Big O notation is a convenient way to describe how fast a function is growing. It is often used in computer science when estimating time complexity.
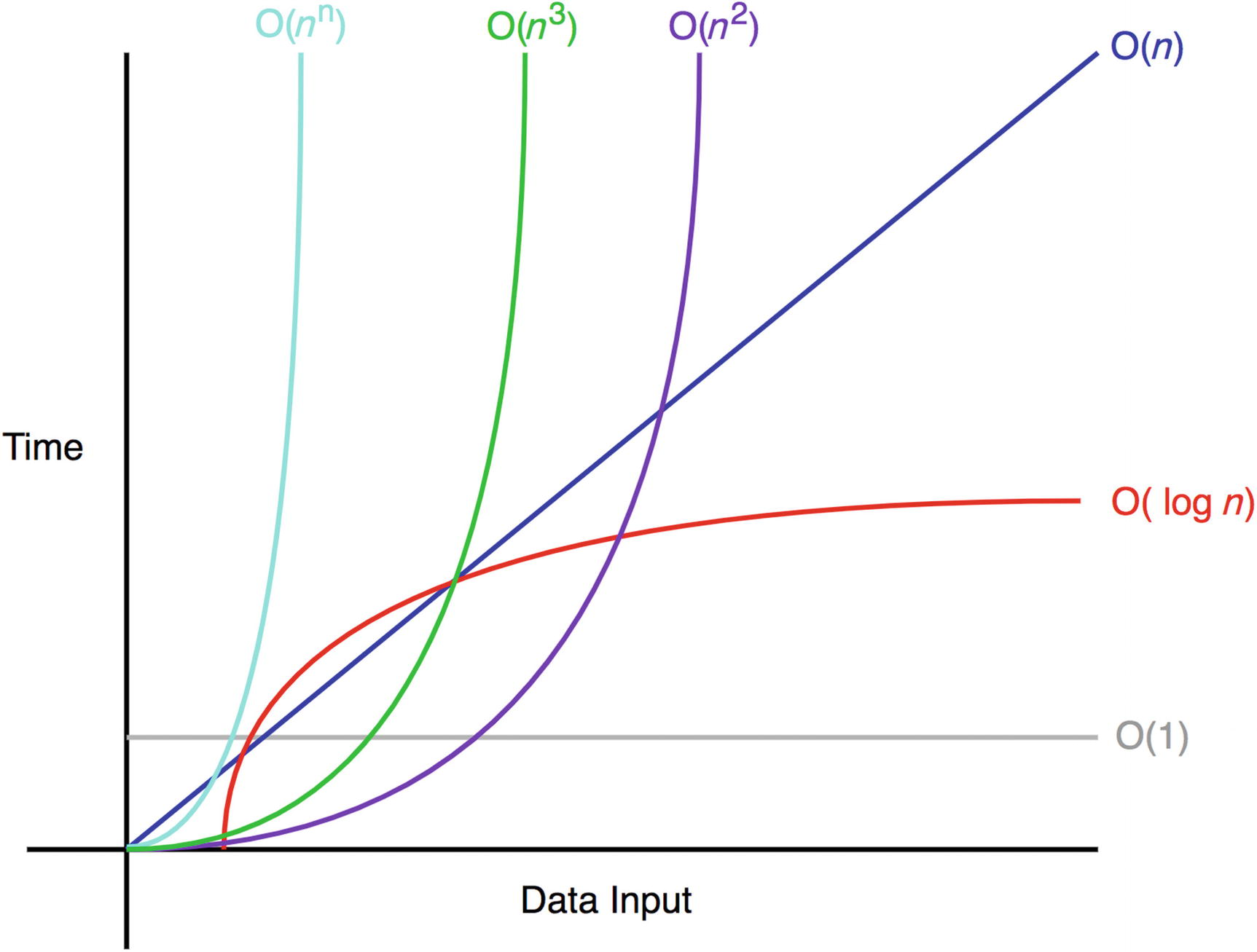
Let's try to analyze the an example
// Find sum of all numbers in array
function sumNumbersInArray(arr) {
let result = 0;
for (let i=0; i < arr.length; i++) {
result += arr[i];
}
return result;
}
and the result
// Find sum of all numbers in array
function sumNumbersInArray(arr) {
let result = 0;
for (let i=0; i < arr.length; i++) {
result += arr[i];
}
return result;
}
Data Input
Operations number
100
1000
10000
100
1000
10000
O(n)
Linear
Example 1
// Calculation
function calculate() {
const a = 3 + 1;
const b = 3 + 3;
console.log('Calculating...');
return a + b;
}
calculate();

Let's analyze example 1
Data Input
Operations number
100
1000
10000
100
1000
10000
O(1)
Constant
Example 1.1
// Calculation
function calculate(c) {
const a = 3 + 1;
const b = 3 + 3;
console.log('Calculating...');
return a + b + c;
}
calculate(3);
How about that?
and it's still O(1)

Example 2
// Calculation
function calculate(arr) {
const a = 3 + 1;
const b = 3 + 3;
let c = 0;
for (let i = 0; i < arr.length; i++) {
c += arr[i];
}
console.log('Calculating...');
return a + b + c;
}
calculate([1,2,3,4,5]);
result - O(n)

Example 3
// Calculation
function calculate(arr) {
const a = 3 + 1;
const b = 3 + 3;
let c = arr.length;
console.log('Calculating...');
return a + b + c;
}
calculate([1,2,3,4,5]);
result - O(1)

Example 4
// Calculation
function calculationInArray(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length; j++) {
arr[i] = arr[i] + arr[j];
}
}
return arr;
}
calculationInArray([1,2,3,4,5]);

Data Input
100
1000
10000
100
1000
10000
O(n2)
quadratic
Example 4 - is quadratic
Operations number
Example 5
// Calculation
function calculationInArray(arr) {
const sum = 0;
arr.forEach(n => {
sum += n;
});
return sum;
}
calculationInArray([1,2,3,4,5]);
result - O(n)

Example 6
// Calculation
function calculationInArray(arr) {
arr.forEach(n => console.log(n));
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length; j++) {
arr[i] = arr[i] + arr[j];
}
}
return arr;
}
calculationInArray([1,2,3,4,5]);
result - O(n) + O(n2) = O(n2)

Example 7
// Calculation
function probablySimpleCalculation(arr) {
let result = 0;
arr.forEach(num => {
const additional = arr.indexOf(num) > 5 ? 5 : 1;
result = result + num + additional;
});
return result;
}
probablySimpleCalculation([1,2,3,4,5,6,7,8]);
result - O(n2), because of indexOf()

Example 7 can be improved
// Calculation
function probablySimpleCalculation(arr) {
let result = 0;
arr.forEach((num, index) => {
const additional = index > 5 ? 5 : 1;
result = result + num + additional;
});
return result;
}
probablySimpleCalculation([1,2,3,4,5,6,7,8]);
result - O(n)
Function growing in numbers
O(1) - 1
Input data - 10000 items
O(n) - 10 000
O(n2) - 100 000 000
O(n3) - 1 000 000 000 000
O(n!) - 100 000 000 000 000 0000 000 000 000000 000 0000 0000 000000 000 000 000 000000 0000000 000000 00000.....

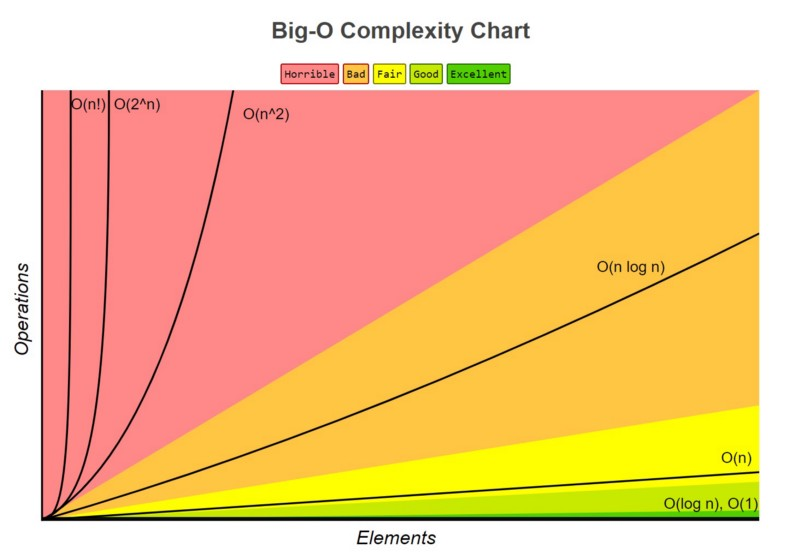
FYI: log 1 = 0; log 10 = 1; log 100 = 2
Big O: Phone book example
-
O(1) (best case): Given the page that a person's name is on and their name, find the phone number.
-
O(log n): Given a person's name, find the phone number by picking a random point about halfway through the part of the book you haven't searched yet, then checking to see whether the person's name is at that point. Then repeat the process about halfway through the part of the book where the person's name lies. (This is a binary search for a person's name.)
-
O(n): Given a phone number, find the person or business with that number.
-
O(n log n): There was a mix-up at the printer's office, and our phone book had all its pages inserted in a random order. Fix the ordering so that it's correct by looking at the first name on each page and then putting that page in the appropriate spot in a new, empty phone book.
-
O(n2): A mistake occurred at the office, and every entry in each of the phone books has an extra "0" at the end of the phone number. Take some white-out and remove each zero.
Now let's see other notations

Big Omega notation (Ω)
It defines a lower bound on order of growth of time taken by an algorithm or code with input size
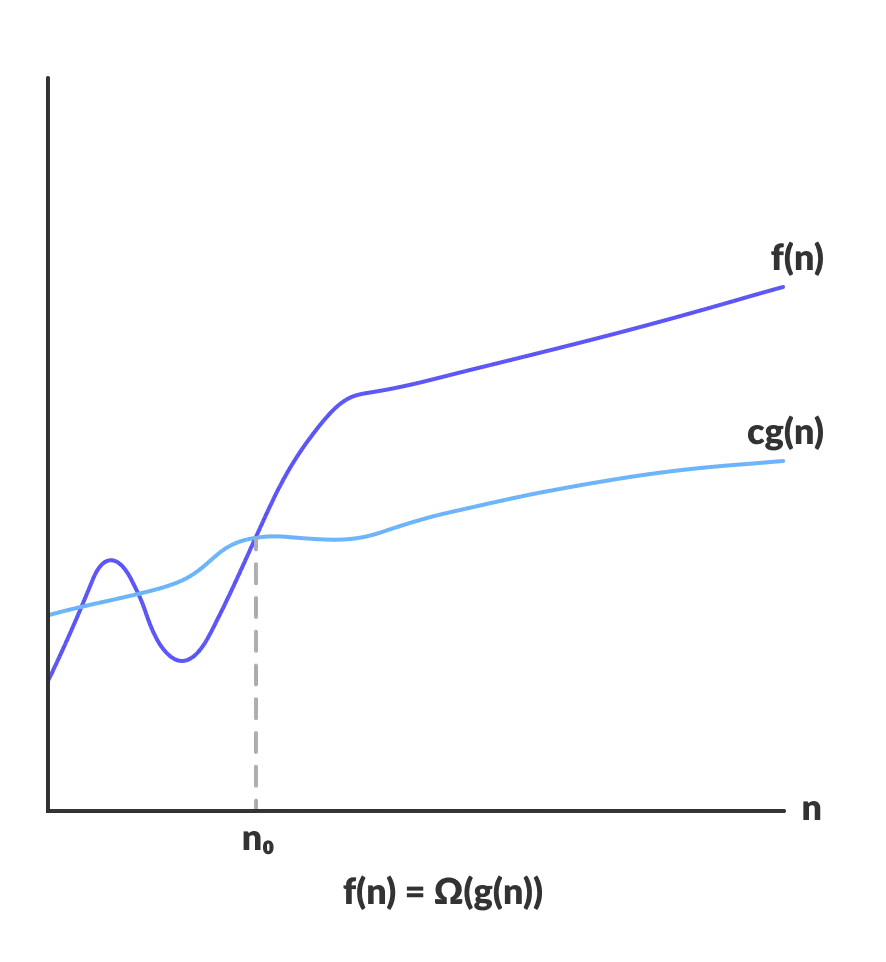
Theta notation (Θ)
It defines exact order of growth of time taken by an algorithm or code with input size
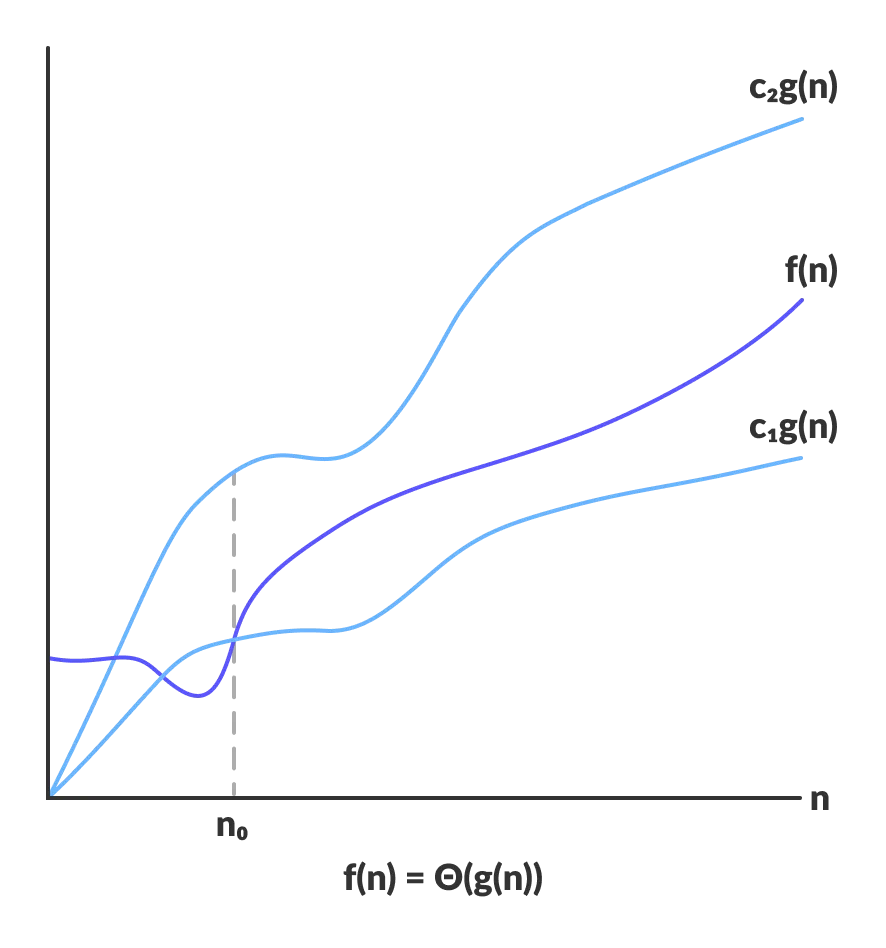
Big O() vs Big Ω() vs Big Θ()
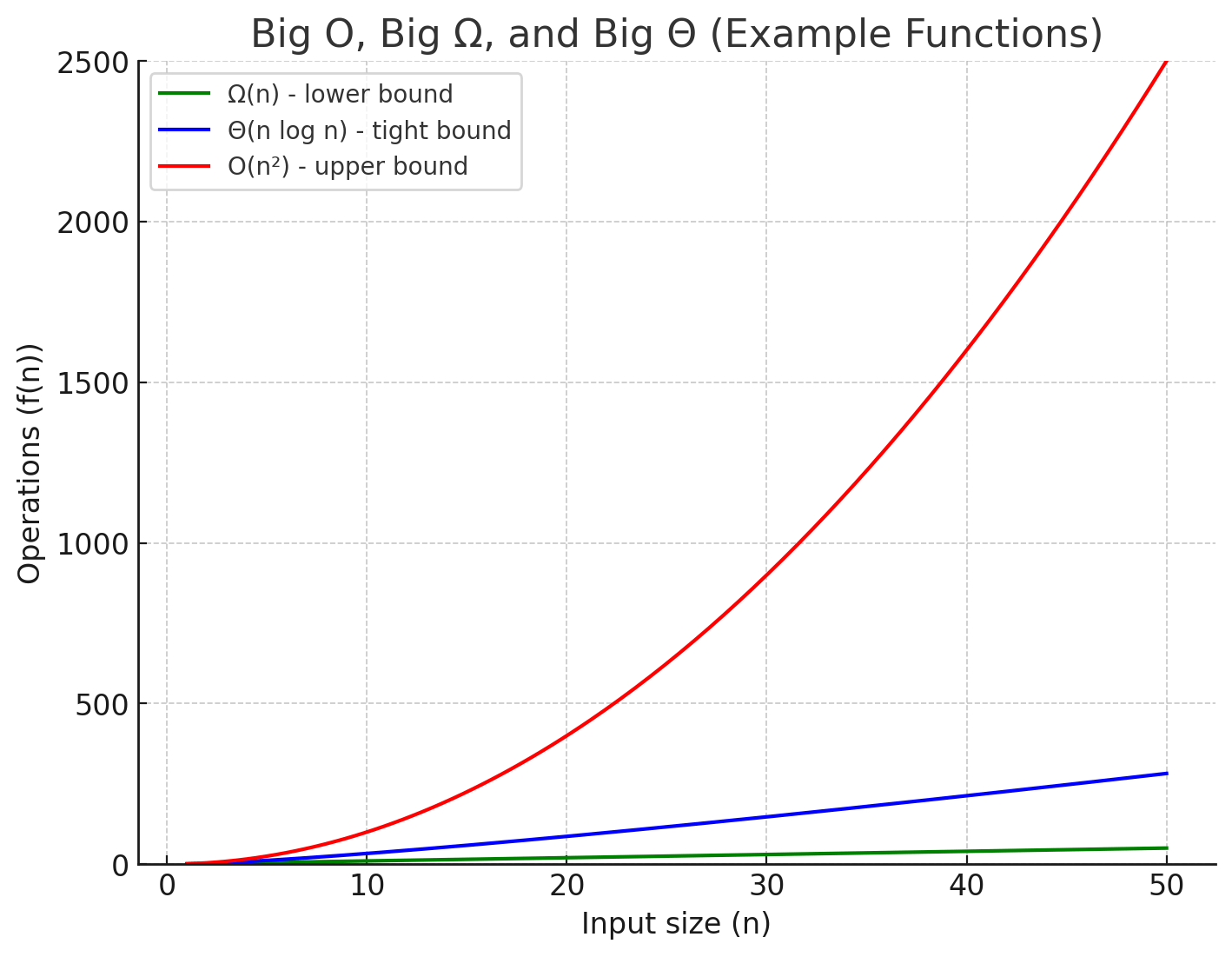
Green line (Ω) → shows the guaranteed minimum growth
Blue line (Θ) → represents a realistic tight bound (here, n log n)
Red line (O) → shows the guaranteed maximum growth
Bubble Sort Complexity
Bubble Sort works by repeatedly swapping adjacent elements if they are in the wrong order.

Worst case (Big O)
-
Array is sorted in reverse order.
-
Algorithm must do the maximum number of swaps and comparisons.
-
Complexity: O(n²)
Best case (Big Ω)
-
Array is already sorted.
-
With an optimization (stop if no swaps in a pass), Bubble Sort only makes one pass.
-
Complexity: Ω(n) (must check each element at least once)
Average case (Big Θ)
-
Random input.
-
On average, about half the elements need swapping each pass.
-
Complexity: Θ(n²)
Types of algorithms and their uses

Types of Algorithm
There are many types of Algorithms, but the fundamental types of Algorithms are:
Recursive Algorithm
Dynamic Programming Algorithm
Divide & Conquer Algorithm
Greedy Algorithm
Brute Force Algorithm
Backtracking Algorithm
Brute Force Algorithm
This is the most basic and simplest type of algorithm. A Brute Force Algorithm is the straightforward approach to a problem i.e., the first approach that comes to our mind on seeing the problem. More technically it is just like iterating every possibility available to solve that problem.
function bruteForceSubstringSearch(text, pattern) {
const textLength = text.length;
const patternLength = pattern.length;
for (let i = 0; i < textLength; i++) {
let j;
for (j = 0; j < patternLength; j++) {
if (text.charAt(i + j) !== pattern.charAt(j)) {
break;
}
}
if (j === patternLength) return i;
}
return textLength;
}
bruteForceSubstringSearch('this is a test', 'test');
Recursive Algorithm
This type of algorithm is based on recursion. In recursion, a problem is solved by breaking it into subproblems of the same type and calling own self again and again until the problem is solved with the help of a base condition.
Some common problem that is solved using recursive algorithms: Factorial of a Number, Fibonacci Series, Depth first search for Graph, etc.
// calculate n! using recursion
function factorial(n) {
if (n <= 1) {
return 1;
} else {
return factorial(n-1) * n;
}
}
factorial(5);
Divide & Conquer Algorithm
Divide and conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type until these become simple enough to be solved directly.
Applications: Binary Search, Quicksort, Merge Sort, Median Finding, Matrix Multiplication, Closest Pair of Points, Strassen’s Algorithm and etc.
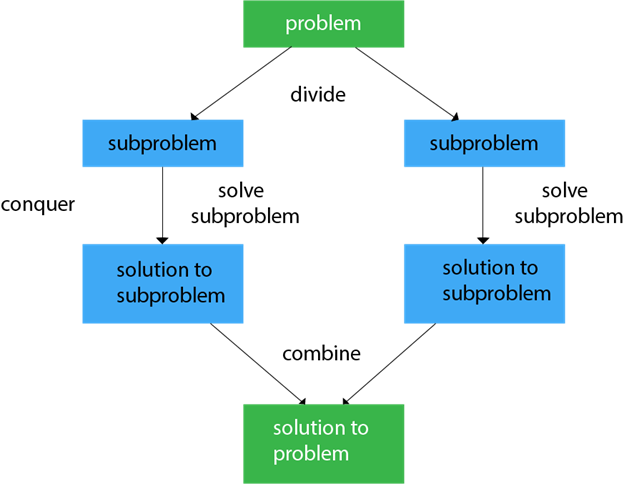

Divide & Conquer Algorithm: Quicksort
const items = [5,3,7,6,2,9];
function quickSort(items, left, right) {
let index;
if (items.length > 1) {
//index returned from partition
index = partition(items, left, right);
//more elements on the left side of the pivot
if (left < index - 1) {
quickSort(items, left, index - 1);
}
//more elements on the right side of the pivot
if (index < right) {
quickSort(items, index, right);
}
}
return items;
}
function swap(items, leftIndex, rightIndex){
const temp = items[leftIndex];
items[leftIndex] = items[rightIndex];
items[rightIndex] = temp;
}
function partition(items, left, right) {
//middle element
const pivot = items[Math.floor((right + left) / 2)],
i = left, //left pointer
j = right; //right pointer
while (i <= j) {
while (items[i] < pivot) { i++; }
while (items[j] > pivot) { j--; }
if (i <= j) {
swap(items, i, j); //sawpping two elements
i++;
j--;
}
}
return i;
}
// first call to quick sort
const sortedArray = quickSort(items, 0, items.length - 1);
console.log(sortedArray); //prints [2,3,5,6,7,9]
Divide & Conquer Algorithm: Palindrome
function palindrome(str) {
const len = str.length;
for (var i = 0; i < len/2; i++) {
if (str[i] !== str[len - 1 - i]) {
// When the characters don't match anymore,
// false is returned and we exit the FOR loop
return false;
}
}
return true;
}sagas => sagas
tenet => tenet
Divide & Conquer Algorithm: Binary Search
function binarySearch(items, value){
let firstIndex = 0,
lastIndex = items.length - 1,
middleIndex = Math.floor((lastIndex + firstIndex)/2);
while(items[middleIndex] != value && firstIndex < lastIndex) {
if (value < items[middleIndex]) {
lastIndex = middleIndex - 1;
} else if (value > items[middleIndex]) {
firstIndex = middleIndex + 1;
}
middleIndex = Math.floor((lastIndex + firstIndex)/2);
}
return (items[middleIndex] != value) ? -1 : middleIndex;
}
const items = [1, 2, 3, 4, 5, 7, 8, 9];
console.log(binarySearch(items, 1));
console.log(binarySearch(items, 5));Dynamic Programming Algorithm
Dynamic Programming is mainly an optimization over plain recursion, as a recursive solution can optimize it using Dynamic Programming. The idea is to simply store the results of subproblems so that we do not have to re-compute them when needed later.
Applications: Fibonacci Sequence, Longest Common Subsequence, Longest Increasing Subsequence, Longest Common substring, Bellman-Ford algorithm, Chain Matrix multiplication, Subset Sum and etc.
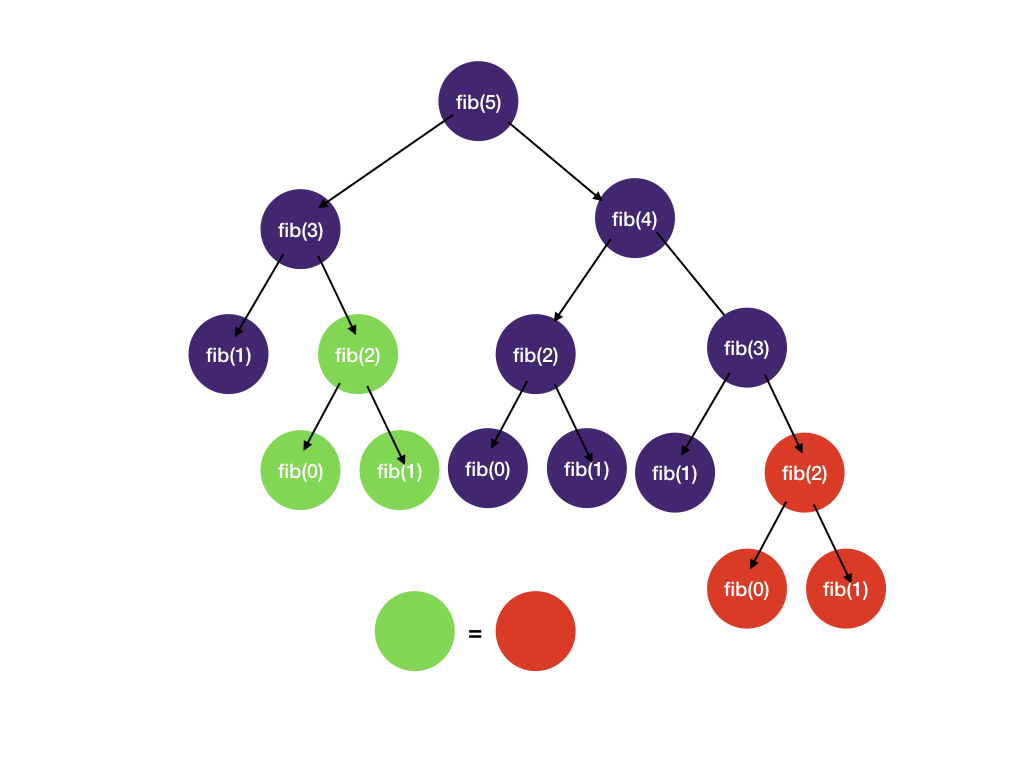
Dynamic Programming Algorithm: Fibonacci sequence
// recursive way
function fibonacci(num) {
if (num <= 1) return 1;
return fibonacci(num - 1) + fibonacci(num - 2);
}
fibonacci(51);
// using memoization
function fibonacci(num, memo) {
memo = memo || {};
if (memo[num]) return memo[num];
if (num <= 1) return 1;
return memo[num] = fibonacci(num - 1, memo) + fibonacci(num - 2, memo);
}
fibonacci(51);
- Time complexity: O(n^2)
- Space complexity: O(n)
- Function calls: 32 billion recursive calls!
- Time needed: an hour
- Time complexity: O(2N)
- Space complexity: O(n)
- Function calls: 99
- Time needed: 0.000001ms
Backtracking Algorithm
Backtracking is an algorithmic technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time (by time, here, is referred to the time elapsed till reaching any level of the search tree).
Applications: Generating all Binary strings, N-Queens Problem, Knapsack Problem, Graph coloring Problem and etc.
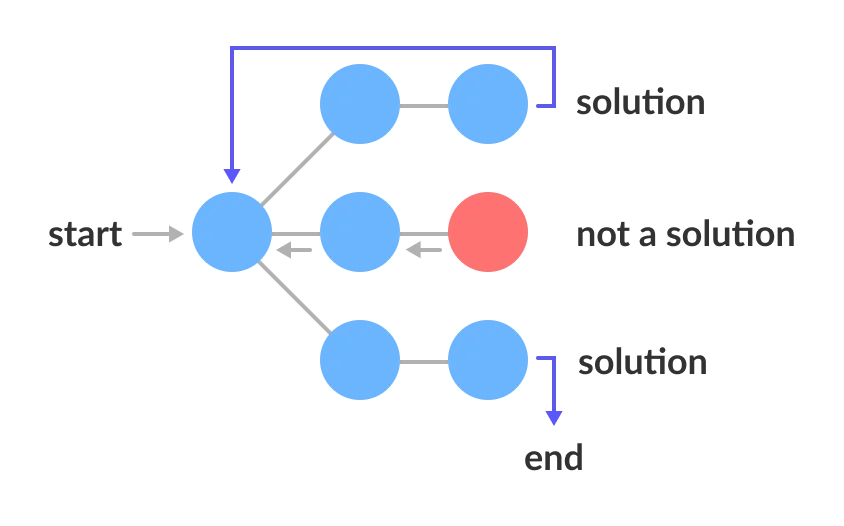
Greedy Algorithm
Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. So the problems where choosing locally optimal also leads to a global solution are best fit for Greedy.
Applications: Huffman Coding Compression, Travelling Salesman Problem, Selection Sort, Topological sort, Prim’s & Kruskal’s algorithms, Coin Change problem, Fractional Knapsack Problem and etc.

Greedy Algorithm: Huffman Coding Compression
class Node {
constructor(count, char, left, right) {
this.count = count;
this.char = char;
this.left = left;
this.right = right;
}
}
class HuffmanCoding {
constructor() {
this.code = {};
this.leafs = null;
this.histogram = {};
this.tree = null;
}
createHistogram(input) {
const histogram = {};
for (let i = 0; i < input.length; i++) {
const code = input.charCodeAt(i);
++histogram[code];
}
this.histogram = histogram;
}
// creates the forest with one tree for every char
createLeafs(histogram) {
this.leafs = Object.entries(histogram).map(([code, freq]) => {
const char = String.fromCharCode(code);
return new Node(freq, char, null, null);
});
}
// splits trees into small and big
splitTrees(forest) {
const sorted = forest.sort((a, b) => a.count - b.count);
const small = sorted.slice(0, 2);
const big = sorted.slice(2);
return [small, big];
}
createTree(forest) {
if (forest.length === 1) return forest[0];
const [small_trees, big_trees] = this.splitTrees(forest);
const new_tree = new Node(
small_trees[0].count + small_trees[1].count,
null,
small_trees[0],
small_trees[1]
);
const new_trees = [...big_trees, new_tree];
return this.createTree(new_trees);
}
isASCII(str) {
const test = /^[\x00-\x7F]*$/.test(str);
return test;
}
// Creates the code-words from the created huffman-tree
createCode(prefix, node) {
// empty root node
if (!node) return {};
// leaf node
if (!node.left && !node.right) {
return { [node.char]: prefix };
}
// recursive call
return {
...this.createCode(prefix + "0", node.left),
...this.createCode(prefix + "1", node.right),
};
}
encode(string) {
if (!this.isASCII(string)) {
return 'Invalid text';
}
this.createHistogram(string);
this.createLeafs(this.histogram);
const tree = this.createTree(this.leafs);
const code = this.createCode("", tree);
const encoded = Array.from(string).map((c) => code[c]);
return {
output: encoded,
code,
};
}
}
const huff = new HuffmanCoding();
console.log(huff.encode('Hello there'));Before we go further, let's become familiar with Flowcharts

Flowchart for algorithms representation

What is Flowchart?
A flowchart is a type of diagram that represents a workflow or process. A flowchart can also be defined as a diagrammatic representation of an algorithm, a step-by-step approach to solving a task.
Start
What to do?
Time to learn 🤓
Time to eat 😋
Lamp doesn't work
Lamp plugged in?
Plug in lamp
No
Replace bulb
Yes
Bulb burned out?
Repair lamp
Yes
No
Types
- Document flowcharts, showing controls over a document-flow through a system
- Data flowcharts, showing controls over a data-flow in a system
- System flowcharts, showing controls at a physical or resource level
- Program flowchart, showing the controls in a program within a system
In addition, many diagram techniques are similar to flowcharts but carry a different name, such as UML or activity diagrams.

UML
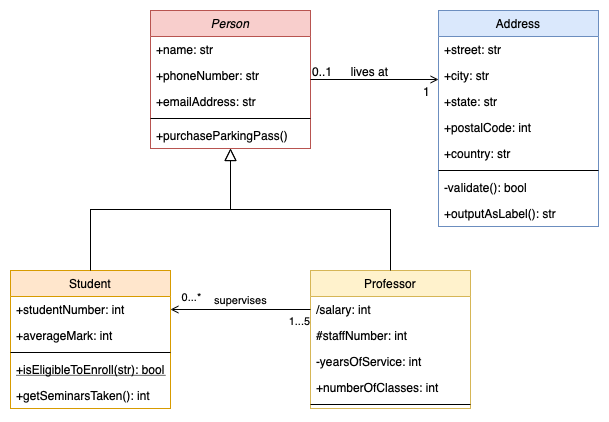
Flowchart of a Web application

Building blocks: common symbols
|
Flowline (Arrowhead) |
Shows the process's order of operation. A line coming from one symbol and pointing at another | |
|
Terminal |
Indicates the beginning and ending of a program or sub-process | |
|
Process |
Represents a set of operations that changes value, form, or location of data | |
|
Decision |
Shows a conditional operation that determines which one of the two paths the program will take | |
|
Input/Output |
Indicates the process of inputting and outputting data, as in entering data or displaying results |
ANSI / ISO shape
Name
Description
Building blocks: other symbols
|
Data File or Database |
Data is represented by a cylinder symbolizing a disk drive. | |
|
Document |
Single or multiple documents represented as a stack of rectangles with wavy bases | |
|
Manual operation |
Represent an operation or adjustment to a process that can only be made manually | |
|
Manual input |
Represented by quadrilateral, with the top irregularly sloping up from left to right, like the side view of a keyboard | |
|
Preparation or initialization |
Originally used for steps like setting a switch or initializing a routine |
Shape
Name
Description





As an example let's build a flowchart, that represents the sum operation

Start
sum = a + b
Enter numbers
a and b
Display sum
End
terminal
process
input and output
Start
Enter numbers
a and b
Display result
End
And now let's try to create a flowchart for the division operation
b is not equal to 0
b number is not valid
Yes
No
result = a / b
Collaborative Live-coding

Task 1
const itemsArray = [
{ a: 1, b: 3 },
{ a: 3, b: 3 },
{ a: 6, b: 3 },
{ a: 10, b: 10 },
{ a: 41, b: 1 },
{ a: 0, b: 4 }
];
function filterAndExtendItems(array) {}We need to filters an array of objects and keep only items, where a > 5 and extend them with a new field sum = a + b
Task 2
const inputStr = "Remember, all I'm offering is the truth. Nothing more.";
function calcStringSymbols(str, symbol) {}We need to calculate the amount of a given symbol in a given string
Task 3
const itemsArrayN = [
{ n: '1' },
{ n: '2' },
{ n: '3' },
{ n: '4' },
{ n: '5' },
];
function reverse(array) {}Reverse an array of items
Task 4
/**
* @param {string} word
* @return {boolean}
*/
function pallindrome(word) {}
/** Palindrome examples:
* anna => anna
* tenent => tenet
*/Check if a word is a palindrome
Task 5
/**
* @param {array} users
* @param {array} cities
* @return {array}
*/
function prepareUsersData(users, cities) {}
/**
* Given data
const usersResp = [
{ name: 'Anna', cityId: '33' },
{ name: 'Taras', cityId: '33' },
];
const citiesResp = [
{ cityId: '30', cityName: 'Kyiv', country: 'Ukraine' },
{ cityId: '33', cityName: 'Lviv', country: 'Ukraine' }
];
*/Transform and prepare users data that should contain the corresponding city information
LeetCode
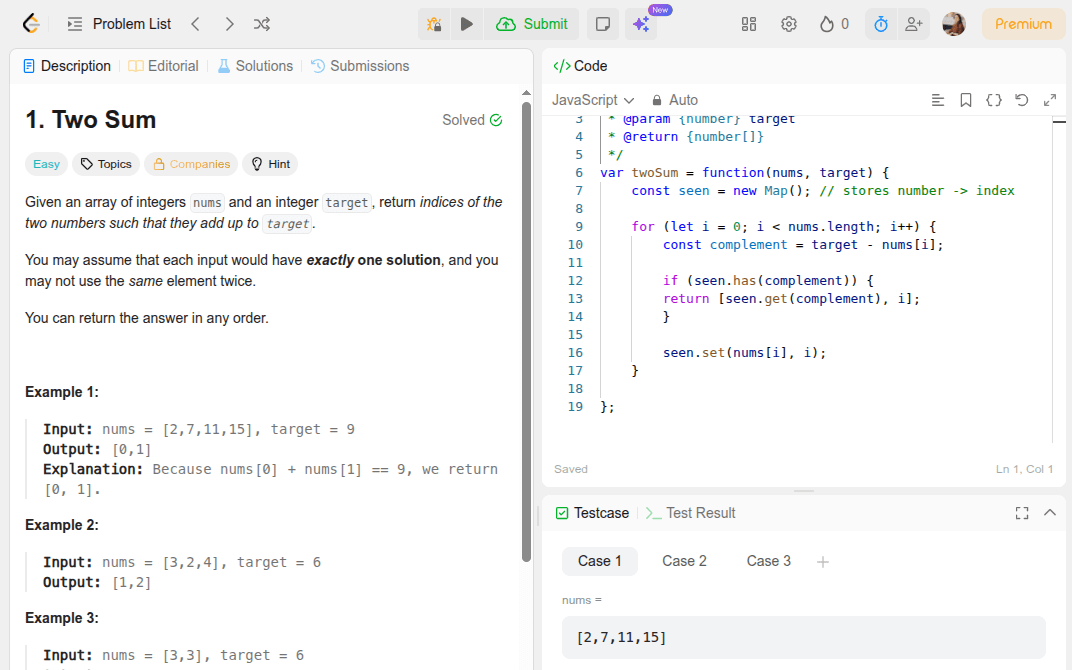
From LeetCode: Palindrome
/**
* @param {string} s
* @return {boolean}
*/
var isPalindrome = function(s) {
};
// Example 1:
// Input: s = "A man, a plan, a canal: Panama"
// Output: true
// Explanation: "amanaplanacanalpanama" is a palindrome.
// Example 2:
// Input: s = "race a car"
// Output: false
// Explanation: "raceacar" is not a palindrome.A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
From LeetCode: Maximum Subarray
/**
* @param {number[]} nums
* @return {number}
*/
const maxSubArray = function(nums) {
};
// Example 1:
// Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
// Output: 6
// Explanation: The subarray [4,-1,2,1] has the largest sum 6.
// Example 2:
// Input: nums = [1]
// Output: 1
// Explanation: The subarray [1] has the largest sum 1.
// Example 3:
// Input: nums = [5,4,-1,7,8]
// Output: 23
// Explanation: The subarray [5,4,-1,7,8] has the largest sum 23.Given an integer array nums, find the subarray with the largest sum, and return its sum.
From LeetCode: Longest substring
/**
* @param {string} s
* @return {number}
* Longest substring without repeating characters
*/
const lengthOfLongestSubstring = function(s) {
};
// Example 1:
// Input: s = "abcabcbb"
// Output: 3
// Explanation: The answer is "abc", with the length of 3.
// Example 2:
// Input: s = "bbbbb"
// Output: 1
// Explanation: The answer is "b", with the length of 1.
// Example 3:
// Input: s = "pwwkew"
// Output: 3
// Explanation: The answer is "wke", with the length of 3.
// Notice that the answer must be a substring, "pwke" is
// a subsequence and not a substring.Given a string s, find the length of the longest substring without duplicate characters.
Task 1: solution
const itemsArray = [
{ a: 1, b: 3 },
{ a: 3, b: 3 },
{ a: 6, b: 3 },
{ a: 10, b: 10 },
{ a: 41, b: 1 },
{ a: 0, b: 4 }
];
function filterAndExtendItems(items) {
return items.reduce((acc, item) => {
if (item.a > 5) {
acc.push({
...item,
sum: item.a + item.b,
});
}
return acc;
}, [])
}Task 2: solution
const inputStr = "Remember, all I'm offering is the truth. Nothing more.";
function calcStringSymbols(str, symbol) {
let amount = 0;
for(let i=0; i<str.length; i++) {
if (str.charAt(i) === symbol) {
amount += 1;
}
}
return amount;
}
calcStringSymbols(inputStr, 'm'); // 4Task 2: solution using Divide & Conquer
const inputStr = "Remember, all I'm offering is the truth. Nothing more.";
function calcStringSymbolsWithDC(str, symbol) {
let amount = 0;
const len = str.length;
for(let i=0; i < len/2; i++) {
if (str.charAt(i) === symbol) {
amount += 1;
}
if (str.charAt(len - i - 1) === symbol) {
amount += 1;
}
}
return amount;
}
calcStringSymbolsWithDC(inputStr, 'm'); // 4Task 3: solution
const itemsArrayN = [
{ n: '1' },
{ n: '2' },
{ n: '3' },
{ n: '4' },
{ n: '5' },
];
function reverse(array) {
return arr.reduceRight((acc, curr) => acc.concat(curr), [])
}Task 4: solution
/**
* @param {string} word
* @return {boolean}
*/
function pallindrome(word) {
// divide & conquer
for (let i = 0; i <= word.length / 2; i++) {
if(word.charAt(i) !== word.charAt(word.length - 1 - i)) {
return false;
} else {
return true;
}
} // O(n/2) => O(n)
}
/** Palindrome examples:
* anna => anna
* tenent => tenet
*/Quiz time
Q & A

Algorithms and Data structures: Part 1
By Inna Ivashchuk
Algorithms and Data structures: Part 1
- 1,723






