Algorithms and Data structures
Lesson 2

$ whoami
Solution Architect
I like JS, React, movies, music and I'm a big fan of LOTR and Star Wars 🤓
May the Force be with you!
8 years with GlobalLogic
about 10 years in Web Development
Trusted Interviewer, speaker, and mentor at GlobalLogic
Part of the program committee at Fwdays

Inna Ivashchuk

Agenda:
- What is a Data structure?
- Types of Data Structures
- Linear DS
- Non-Linear DS
- Big O() of сommon Data Structure operations
- How to choose the right data structure?
- Collaborative Live-coding
What is Data structure?

A data structure is a specialized format for organizing, processing, retrieving and storing data.
What is a Data structure?
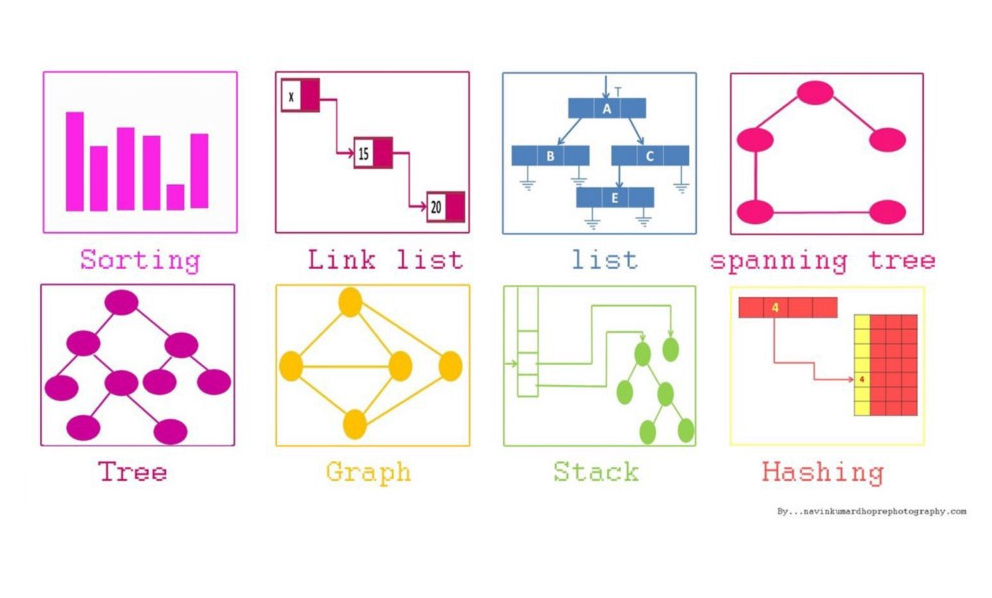
How are data structures used

Storing data (DB)
Managing resources and services (OS)
Data Exchange (TCP/IP)
Ordering and sorting
Indexing
Scalebility (Apache Spark)
and many other places
Types of Data structures

JavaScript Data Types
Data Types
Primitive
Non-Primitive
null
undefined
number
boolean
string
symbol
Object
Data structure hierarchy
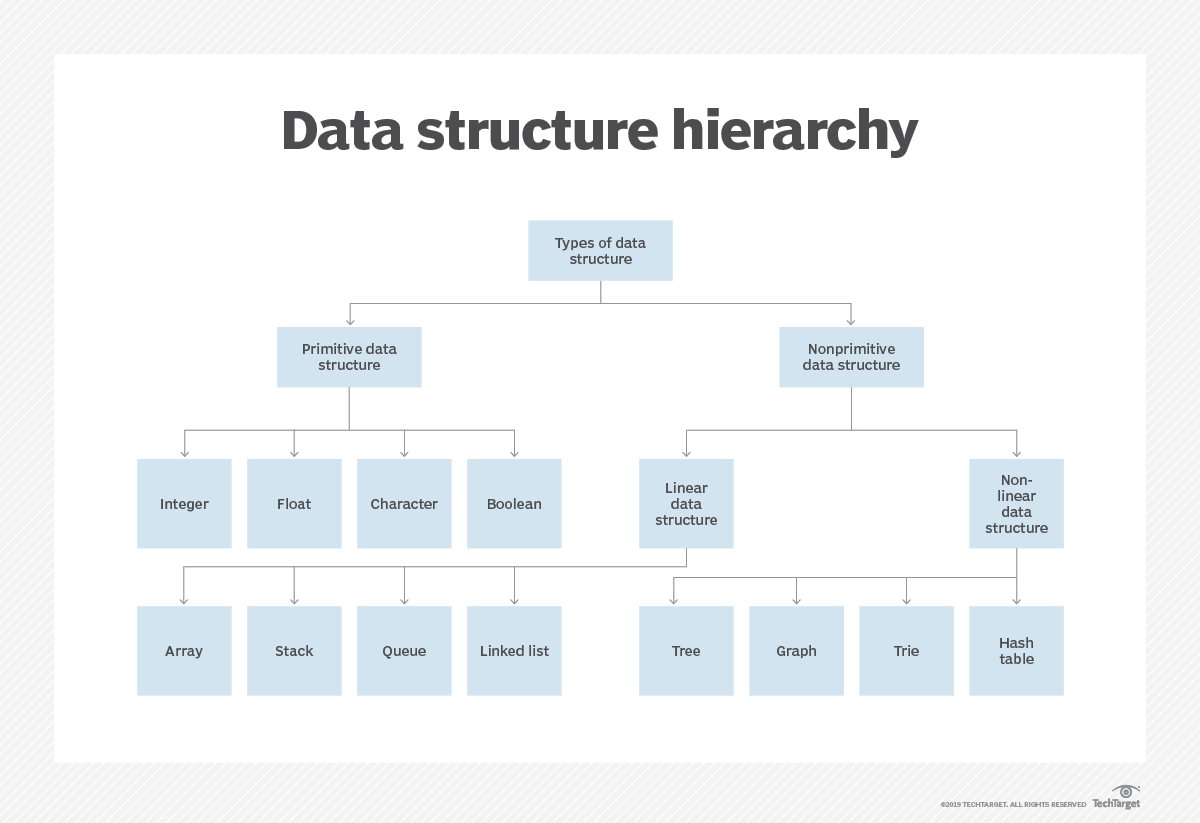
Linear Data Structures

An array is a collection of items stored at contiguous memory locations. The idea is to store multiple items of the same type together.
Can be one and multi-dimensional.
Array
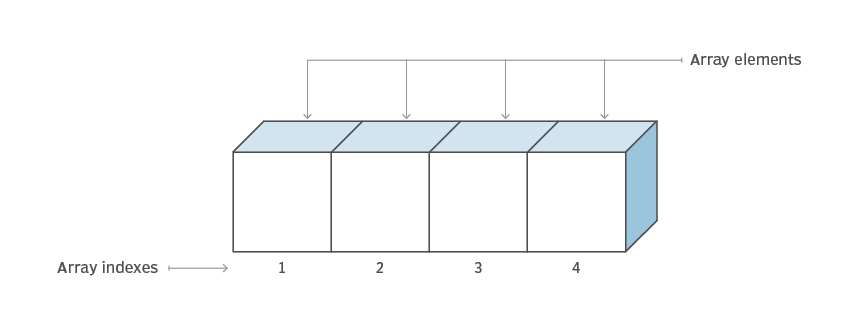
0 1 2 3
Array
20
10
3
13
9
0
1
2
3
4
20
10
3
13
9
How we perceive an array:
How it is stored in memory
Consecutive memory locations
RAM
Some data types
An array
Array: types
20
10
3
13
9
0
1
2
3
4
20
10
3
13
9
2
11
9
3
9
0
1
2
3
4
20
10
3
13
9
2
11
9
3
9
0
1
2
3
4
100
1
33
3
One-dimensional array
Multidimensional array
Two-dimensional array
0
1
2
0
1
Array: types
// One-dimensional
const movies = [
"Star Wars",
"The Lord of the Rings",
"Harry Potter",
"The Matrix",
"Dune",
];
console.log(movies[3]);
// Two-dimensional
const matrix = [
[1, 2, 3],
[4, 5, 6]
];
console.log(matrix[1][1]);
// Multidimensional
const terrains = [
['desert', 'desert', 'grass', 'grass'],
['desert', 'grass', 'water', 'grass'],
['grass', 'grass', 'water', 'water'],
['grass', 'grass', 'grass', 'grass']
];
console.log(terrains[1][0]);Stack is a linear data structure that follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).
Stack
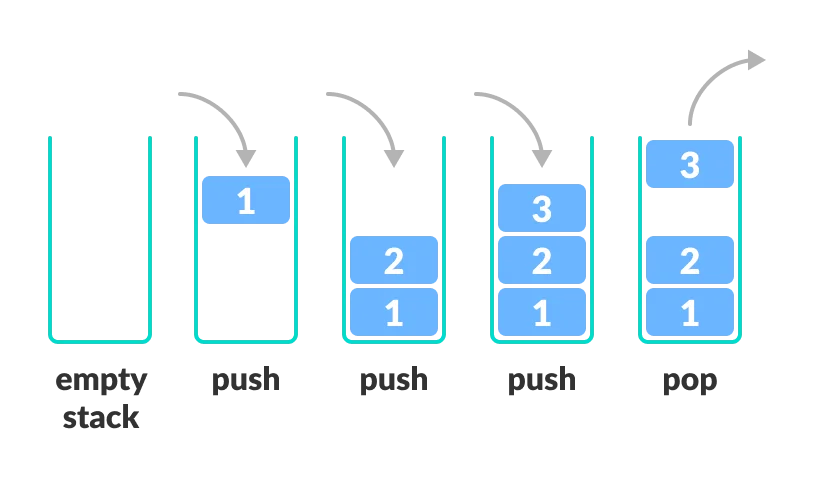
Stack: JS implementation
// Stack class
class Stack {
// Array is used to implement stack
constructor() {
this.items = [];
}
// push method
push(element) {
// push element into the items
this.items.push(element);
}
// pop method
pop() {
// return top most element in the stack
// and removes it from the stack
// Underflow if stack is empty
if (this.items.length == 0)
return "Underflow";
return this.items.pop();
}
// peek method
peek() {
// return the top most element from the stack
// but does'nt delete it.
return this.items[this.items.length - 1];
}
// isEmpty method
isEmpty() {
// return true if stack is empty
return this.items.length == 0;
}
// printStack method
printStack() {
var str = "";
for (var i = 0; i < this.items.length; i++)
str += this.items[i] + " ";
return str;
}
}
const stack = new Stack();
// Adding element to the stack
stack.push(10);
stack.push(20);
stack.push(30);
// Printing the stack element
// prints [10, 20, 30]
console.log(stack.printStack());
// returns 30
console.log(stack.peek());
// returns 30 and remove it from stack
console.log(stack.pop());
// returns [10, 20]
console.log(stack.printStack());
A Queue is a linear structure that follows a particular order in which the operations are performed. The order is First In First Out (FIFO)
Queue

Queue: JS implementation
// Queue class
class Queue {
// Array is used to implement a Queue
constructor() {
this.items = [];
}
// Functions to be implemented
// enqueue method
enqueue(element) {
// adding element to the queue
this.items.push(element);
}
// dequeue method
dequeue() {
// removing element from the queue
// returns underflow when called
// on empty queue
if (this.isEmpty())
return "Underflow";
return this.items.shift();
}
// front method
front() {
// returns the Front element of
// the queue without removing it.
if (this.isEmpty())
return "No elements in Queue";
return this.items[0];
}
// isEmpty method
isEmpty() {
// return true if the queue is empty.
return this.items.length == 0;
}
// printQueue method
printQueue() {
var str = "";
for (var i = 0; i < this.items.length; i++)
str += this.items[i] + " ";
return str;
}
}
// creating object for queue class
const queue = new Queue();
// Testing dequeue and pop on an empty queue
// returns Underflow
console.log(queue.dequeue());
// returns true
console.log(queue.isEmpty());
// Adding elements to the queue
// queue contains [10, 20, 30, 40, 50]
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
queue.enqueue(40);
queue.enqueue(50);
queue.enqueue(60);
// returns 10
console.log(queue.front());
// removes 10 from the queue
// queue contains [20, 30, 40, 50, 60]
console.log(queue.dequeue());
// returns 20
console.log(queue.front());
// removes 20
// queue contains [30, 40, 50, 60]
console.log(queue.dequeue());
// printing the elements of the queue
// prints [30, 40, 50, 60]
console.log(queue.printQueue());
Stack vs Queue




Last In First Out
LIFO
FIFO
First In First Out
A Linked List stores a collection of items in a linear order. Each element, or node, in a Linked list, contains a data item, as well as a reference, or link, to the next item in the list.
Linked List

Linked List

Node
class Node {
constructor(value, next) {
this.value = value;
this.next = null;
}
}

Linked List: JS implementation
class Node {
constructor(value, next) {
this.value = value;
this.next = null;
}
}
class List {
constructor() {
this.head = null;
this.tail = null;
}
getNode(index) {
if (index < 0) return 0;
if (index === 0 && this.head) return this.head;
let currentNode = this.head;
while (index > 0 && currentNode && currentNode.next) {
currentNode = currentNode.next;
index--;
}
if (index !== 0) {
return null;
}
return currentNode;
}
get(index) {
return this.getNode(index).value;
}
push(value) {
if (!this.head) {
this.head = new Node(value);
this.tail = this.head;
return this;
}
this.tail.next = new Node(value);
this.tail = this.tail.next;
return this;
}
pop() {
if (!this.head) {
return null;
}
if (!this.head.next) {
const temp = this.head.value;
this.head = this.tail = null;
return temp;
}
let currentNode = this.head;
while (currentNode.next.next !== null) {
currentNode = currentNode.next;
}
const temp = this.tail.value;
this.tail = currentNode;
currentNode.next = null;
return temp;
}
remove(index) {
const prev = this.getNode(index - 1);
const current = this.getNode(index);
if (prev && current && current.next) {
prev.next = current.next;
} else if (!prev && current) {
this.head = current.next;
}
return current;
}
shift() {
if (this.head) {
const temp = this.head.value;
if (this.head.next === null) {
this.tail = null;
}
this.head = this.head.next;
return temp;
}
return null;
}
unshift(value) {
const newNode = new Node(value);
newNode.next = this.head;
this.head = newNode;
return this;
}
toString() {
let result = '';
let current = this.head;
while (current) {
result += `${current.value}${current.next ? ', ' : ''}`;
current = current.next;
}
return result;
}
}
const list = new List();
list.push(1).push(2).push(3).push(4);
console.log(list.toString());
console.log(list.remove(1));
console.log(list.toString());
console.log(list.remove(0));
console.log(list.toString());
console.log(list.remove(333));
console.log(list.toString());Non-Linear Data Structures

A Hash table (also known as a Hash map) - stores a collection of items in an associative array that plots keys to values. A Hash table uses a hash function to convert an index into an array of buckets that contain the desired data item.
Hash Table
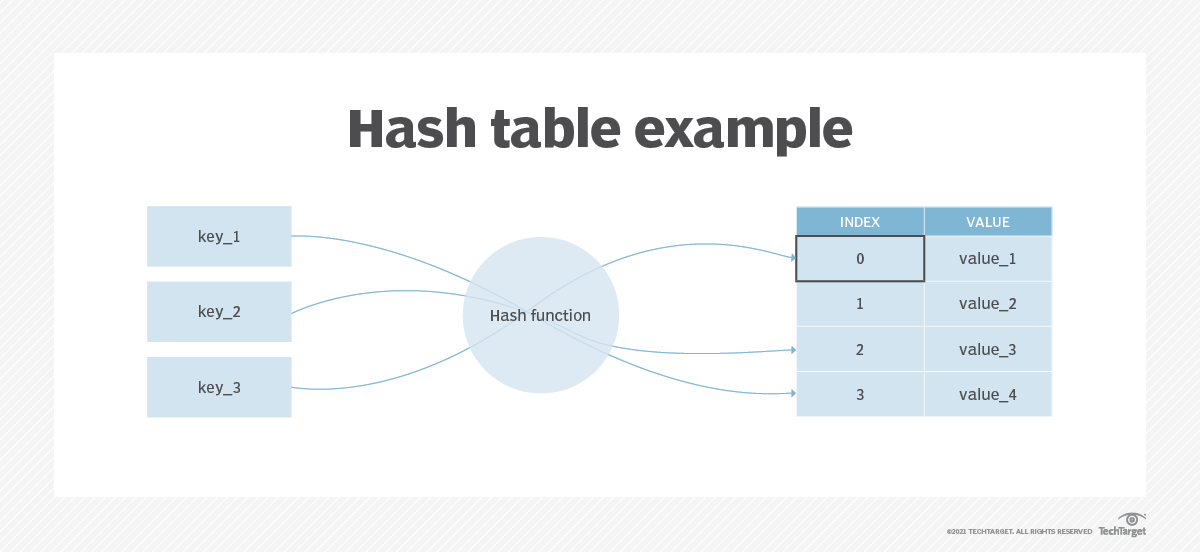
Hash Table: JS implementation
const WEIRD_NUMBER = 23;
function hash(str, limit = 53) {
let result = 0;
for(let i=0; i < Math.min(str.length, 100); i++) {
result += (str.charCodeAt(i) - 96) * WEIRD_NUMBER;
}
return Math.abs(result % limit);
}
class HashTable {
constructor() {
this.array = new Array(10);
}
set(key, value) {
const keyHash = hash(key, this.array.length);
if(!this.array[keyHash]) {
this.array[keyHash] = [];
}
const bucket = this.array[keyHash];
bucket.push([key, value]);
}
get(key) {
const keyHash = hash(key, this.array.length);
const bucket = this.array[keyHash];
for(let i = 0; i < bucket.length; i++) {
const entries = bucket[i];
if (entries[0] === key) {
return entries[1];
}
}
return;
}
keys() {
const result = [];
for (let i = 0; i < this.array.length; i++) {
if(this.array[i]) {
this.array[i].forEach(entry => {
result.push(entry[0]);
});
}
}
return result;
}
}
const test = new HashTable();
test.set('black', '#000');
test.set('white', '#fff');
test.set('red', '#f00');
test.set('blue', '#00f');
test.set('green', '#0f0');
console.log(test);
console.log(test.get('green'));
console.log(test.get('black'));
console.log(test.get('red'));
console.log(test.get('white'));
console.log(test.keys());Map vs Object
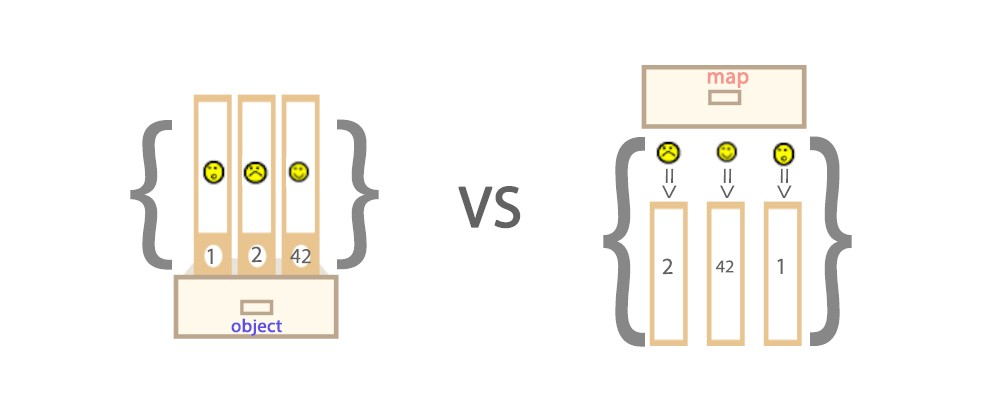
Map is a data collection type (in a more fancy way — abstract data structure type), in which, data is stored in a form of pairs, which contains a unique key and value mapped to that key. And because of the uniqueness of each stored key, there is no duplicate pair stored.
Use Map, when many changes expected
const map1 = new Map();
map1.set('a', 1);
map1.set('b', 2);
map1.set('c', 3);
console.log(map1.get('a'));
// Expected output: 1
map1.set('a', 97);
console.log(map1.get('a'));
// Expected output: 97
console.log(map1.size);
// Expected output: 3
map1.delete('b');
console.log(map1.size);
// Expected output: 2
Set
A JavaScript Set is a collection of unique values of any type, whether primitive values or object references. The main things to know:
- each value can only occur once in a Set
- can hold any value of any data type.
'Ron'
25
'QA'
'QA lead'
MAP
Keys
'name'
'age'
'job'
'title'
Values
'Ron'
'John'
'Alex'
'Juli'
SET
Indices
0
1
2
3
Values
A Tree stores a collection of items in an abstract, hierarchical way. Each node is associated with a key-value, with parent nodes linked to child nodes - or subnodes. There is one root node that is the ancestor of all the nodes in the tree.
Trees
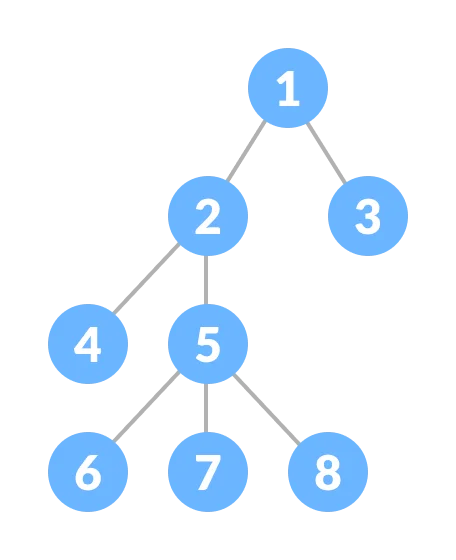
Binary Tree
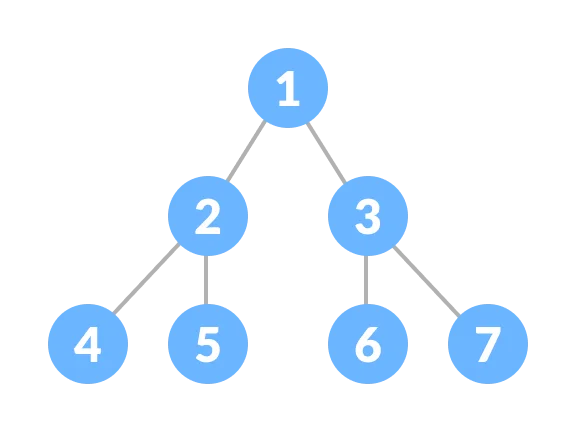
Root (onle one)
Child
Leaf (no children)
Binary Search Tree: JS implementation
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
// Add new Node with {value}
add(value) {
if(!this.root) {
this.root = new Node(value);
return this;
}
let temp = this.root;
while(true) {
if(temp.value < value) {
if (!temp.right) {
temp.right = new Node(value);
return this;
}
temp = temp.right;
} else {
if(!temp.left) {
temp.left = new Node(value);
return this;
}
temp = temp.left;
}
}
}
// Find Node with {value}
find(value) {
let temp = this.root;
if(!temp) {
return null;
}
while(true) {
if(temp.value === value) {
return temp;
} else if (temp.value < value) {
if(!temp.right) {
return null;
}
temp = temp.right;
} else {
if (!temp.left) {
return null;
}
temp = temp.left;
}
}
}
// Check if Node with {value} exists
contains(value) {
let node = this.find(value);
if (node) {
return true;
}
return false;
}
// Traversing
// B
// A C
// A, B, C
traverseInOrder(node = this.root) {
let res = [];
function traverse(node) {
if (node.left) {
traverse(node.left)
}
res.push(node.value)
if (node.right) {
traverse(node.right)
}
}
traverse(node);
return res;
}
// B, A, C
traversePreorder(node = this.root) {
return node
? [node.value, ...this.traversePreorder(node.left), ...this.traversePreorder(node.right)]
: [];
}
// A, C, B
traversePostorder() {
let res = [];
function traverse(node) {
if (node.left) {
traverse(node.left)
}
if (node.right) {
traverse(node.right)
}
res.push(node.value)
}
traverse(this.root);
return res;
}
}
const tree = new BinarySearchTree();
tree.add(5).add(2).add(-1).add(6).add(100);
// console.log(tree);
// 5
// 2 6
// 100
console.log(tree.find(2));
console.log(tree.find(100));
console.log(tree.find(1000000));
console.log(tree.contains(2));
console.log(tree.contains(17));
console.log('Preorder ', tree.traversePreorder());
console.log('Inorder ', tree.traverseInOrder());
console.log('Postorder ', tree.traversePostorder());
A Heap is a tree-based structure in which each parent node's associated key value is greater than or equal to the key values of any of its children's key values.
Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly.
Heap
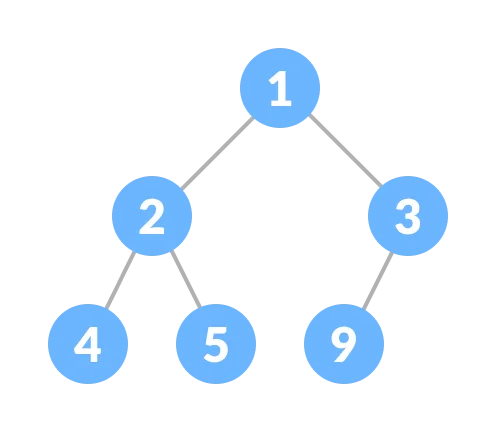
Heap: max and min
Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
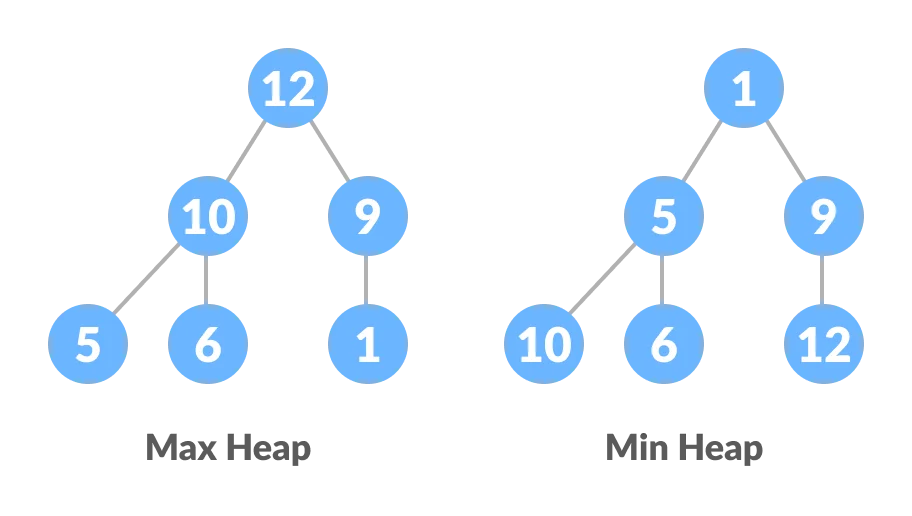
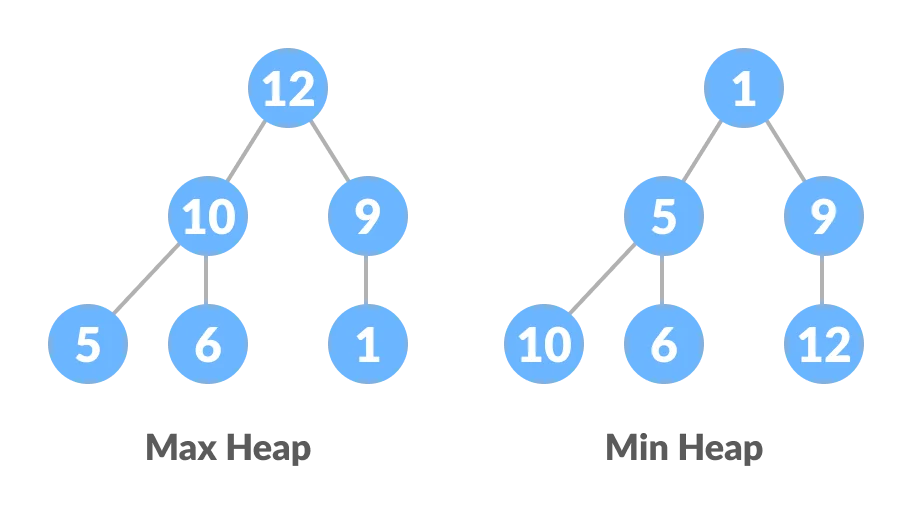
Heap: JS implementation
function Heap(data = []) {
this.data = data;
this.size = data.length;
if (data.length > 1) {
this.buildMaxHeap();
}
}
Heap.prototype = {
swap: function(i, j) {
let temp = this.data[i];
this.data[i] = this.data[j];
this.data[j] = temp;
},
maxHeapify: function(i) {
let leftIdx = 2*i + 1;
let rightIdx = 2*i + 2;
let largest = i;
if ( leftIdx < this.size && this.data[leftIdx] > this.data[largest]) {
largest = leftIdx;
}
if (rightIdx < this.size && this.data[rightIdx] > this.data[largest]) {
largest = rightIdx;
}
if (largest !== i) {
this.swap(largest, i);
this.maxHeapify(largest);
}
},
buildMaxHeap: function() {
for(let i = Math.floor(this.size / 2); i >= 0; i--) {
this.maxHeapify(i);
}
},
bubbleUp: function() {
let curIdx = this.size - 1;
while(curIdx > 0) { // O(log(n)) as we deviding parent index by 2 every iteration
let parentIdx = Math.floor((curIdx - 1)/ 2);
let lastVal = this.data[curIdx];
let parentData = this.data[parentIdx];
if (parentData >= lastVal) { return; }
else {
this.data[parentIdx] = lastVal;
this.data[curIdx] = parentData;
curIdx = parentIdx;
}
}
},
push: function(val) {
this.data.push(val);
this.size++;
this.bubbleUp();
},
decrementSize: function() { this.size--; },
print: function() { console.log(this.data) }
}
const heap = new Heap();
heap.push(20);
heap.push(10);
heap.push(30);
heap.push(1);
heap.push(100);
heap.print();
/*
Output:
[ 100, 30, 20, 1, 10 ]
The tree looks like:
100
/ \
30 20
/ \
1 10
*/
A Graph stores a collection of items in a nonlinear fashion. Graphs are made up of a finite set of nodes, also known as vertices, and lines that connect them, also known as edges. These are useful for representing real-world systems such as computer networks.
Graph
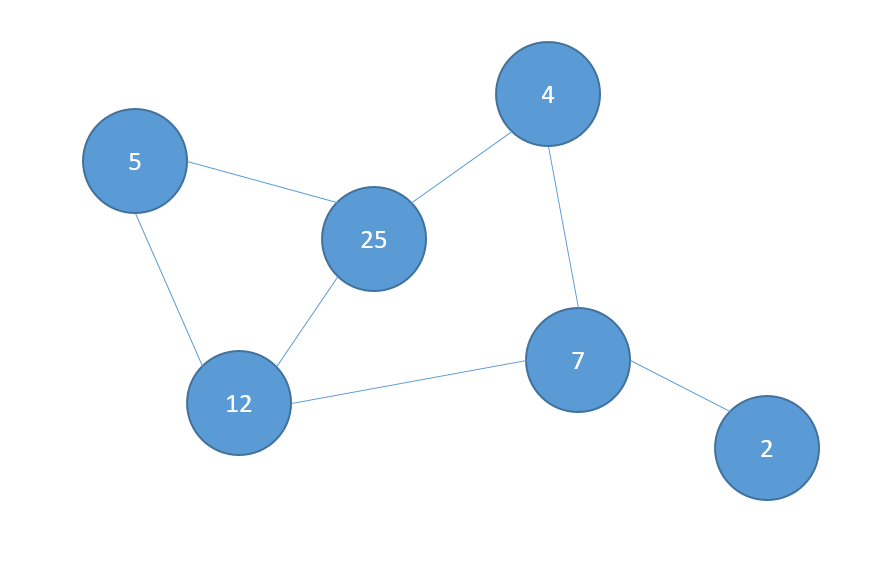
Graph: Weighted Graph
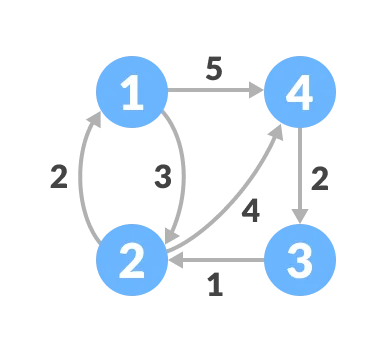
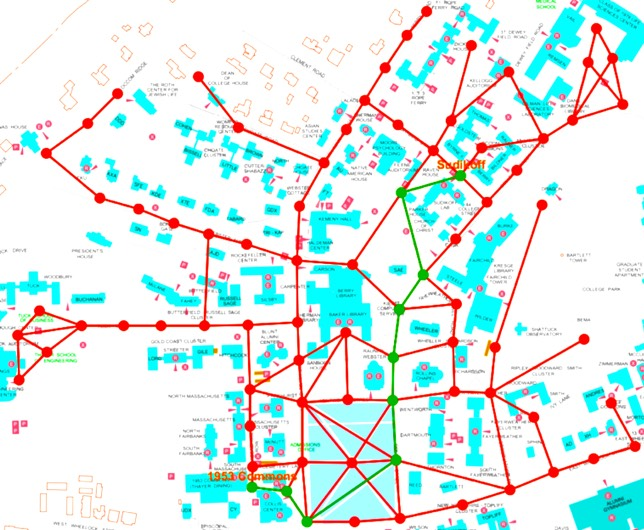
Weighted Graph: JS implementation
class PriorityQueue {
constructor(){
this.values = [];
}
enqueue(val, priority) {
this.values.push({val, priority });
this.sort();
}
dequeue() {
return this.values.shift();
}
sort() {
this.values.sort((a, b) => a.priority - b.priority);
};
}
class WeightedGraph {
/**
* In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph
*/
constructor() {
this.adjacencyList = {};
}
/**
* "Vertex" is a synonym for a node of a graph, i.e., one of the points on which the graph is defined and which may be connected by graph edges.
*
* Time complexity: O(1)
*/
addVertex(vertex) {
if(this.adjacencyList[vertex]) {
console.warn(`"${vertex}" vertex already present into adjacency list. Overriding ${vertex} `);
}
this.adjacencyList[vertex] = [];
}
/**
* For an undirected graph, an unordered pair of nodes that specify a line joining these two nodes are said to form an edge.
*
* Time complexity: O(1)
*/
addEdge(vertex1, vertex2, weight) {
if(!this.adjacencyList[vertex1]) {
console.info(`Creating vertex "${vertex1}"`)
this.addVertex(vertex1);
}
if(!this.adjacencyList[vertex2]) {
console.info(`Creating vertex "${vertex2}"`)
this.addVertex(vertex2);
}
this.adjacencyList[vertex1].push({ node: vertex2, weight });
this.adjacencyList[vertex2].push({ node: vertex1, weight });
}
// O(|E|)
removeEdge(vertex1, vertex2) {
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(val => val !== vertex2);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(val => val !== vertex1);
}
// O(|V| + |E|)
removeVertex(vertex) {
this.adjacencyList[vertex]
.forEach(vertex2 => this.removeEdge(vertex, vertex2));
delete this.adjacencyList[vertex];
}
/**
* Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures.
* It starts at the tree root and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
*/
breadthFirstSearch() {
const res = [];
const keys = Object.keys(this.adjacencyList);
const queue = [keys[0]];
const visited = { [keys[0]]: true };
while(queue.length) {
const node = queue.shift();
res.push(node);
this.adjacencyList[node].forEach(vrt => {
if(!visited[vrt.node]) {
visited[vrt.node] = true;
queue.push(vrt.node);
}
});
}
return res;
}
/**
* Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures.
* The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph)
* and explores as far as possible along each branch before backtracking.
*/
depthFirstSearch() {
const res = [];
const keys = Object.keys(this.adjacencyList);
const visited = {};
const traverse = node => {
if (!visited[node]) {
visited[node] = true;
res.push(node);
this.adjacencyList[node].forEach(vrt => traverse(vrt.node))
}
}
traverse(keys[0]);
return res;
}
/**
*
* Dijkstra's algorithm (or Dijkstra's Shortest Path First algorithm, SPF algorithm)[1] is an algorithm for finding the shortest paths
* between nodes in a graph, which may represent, for example, road networks.
*
* It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
*/
dijkstra(vertex1, vertex2) {
const previous = {};
const dist = {};
const keys = Object.keys(this.adjacencyList);
const priorityQueue = new PriorityQueue();
let smallest;
// init
keys.forEach(key => {
if (key === vertex1) {
dist[key] = 0;
priorityQueue.enqueue(key, 0);
} else {
dist[key] = Infinity;
priorityQueue.enqueue(key, Infinity);
}
previous[key] = null;
});
// take smallest dist vertex
while(priorityQueue.values.length) {
smallest = priorityQueue.dequeue().val;
if(smallest === vertex2) {
// wohoo
const res = [];
let curr = previous[vertex2]
while(curr) {
res.push(curr);
curr = previous[curr];
}
return res.reverse().concat(vertex2);
}
this.adjacencyList[smallest].forEach(el => {
// calc dist to neighbour node
let candidate = el.weight + dist[smallest];
if (dist[el.node] > candidate) {
dist[el.node] = candidate;
previous[el.node] = smallest;
priorityQueue.enqueue(el.node, candidate)
}
})
}
}
}
/**
* Example:
*
* 7
* C --- D
* 1 / 3 \ 2
* A ------- B
* 3 | 2 | 5
* F ------- K
* 4 \ 1 / 1
* J ---- I
*
*/
const graph = new WeightedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('F');
graph.addVertex('K');
graph.addVertex('J');
graph.addVertex('I');
graph.addEdge('C', 'D', 7);
graph.addEdge('A', 'B', 3);
graph.addEdge('F', 'K', 2);
graph.addEdge('J', 'I', 1);
graph.addEdge('C', 'A', 1);
graph.addEdge('A', 'F', 3);
graph.addEdge('F', 'J', 4);
graph.addEdge('D', 'B', 2);
graph.addEdge('B', 'K', 5);
graph.addEdge('K', 'I', 1);
console.log(graph.breadthFirstSearch());
console.log(graph.depthFirstSearch());
console.log('A->D', graph.dijkstra('A', 'D'));
console.log('A->K', graph.dijkstra('A', 'K'));
console.log('A->I', graph.dijkstra('A', 'I'));
A Trie, also known as a keyword tree, is a data structure that stores strings as data items that can be organized in a visual graph.
Trie
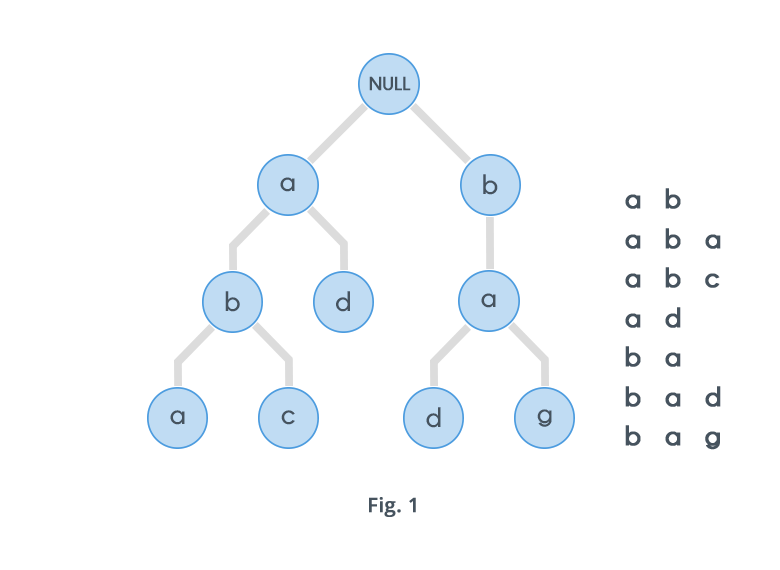
Big O() of сommon Data Structure operations

Common Data Structure Operations
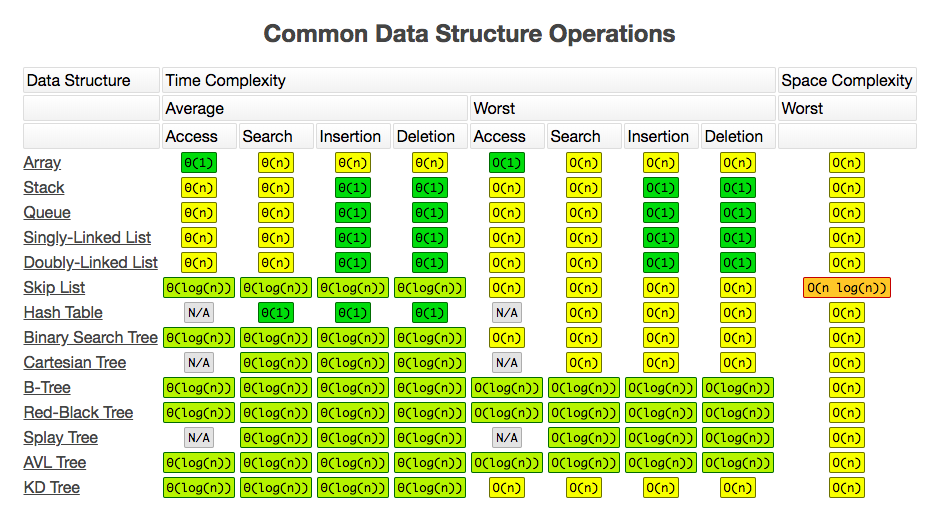
Big O for JavaScript array methods
const movies = [
'LoTR',
'Back to the Future',
];
// .push() - add a new element
values.push('Star Wars', 'Matrix');
// .pop() - remove the last one
values.pop();
// .reverse() - reverse an array
values.reverse();
// .unshift() // add a new elemnt
// to the beginning of an array
values.unshift('Avatar');
// .sort()
values.sort();
// .filter()
values.filter();
=> O(1)
=> O(1)
=> O(n)
=> O(n)
=> O(n log (n))
=> O(n)
Array Sorting Algorithms
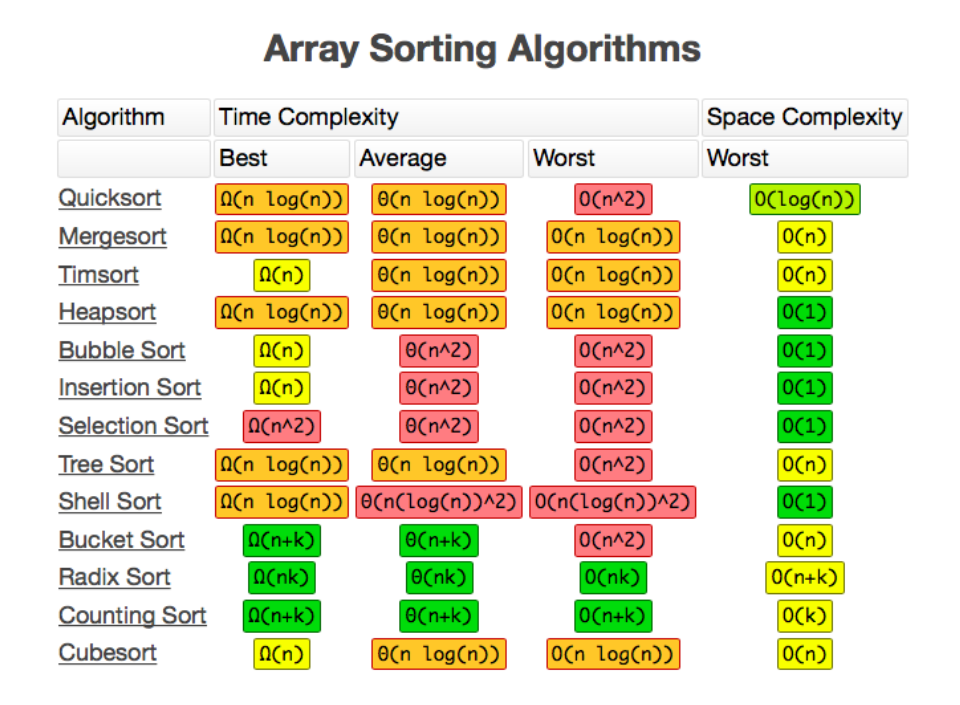
How to choose the right Data Structure

What operations matter most?
-
Do you need fast lookups? → HashMap/Set
-
Do you need ordered traversal? → Tree, Sorted Array
-
Do you need FIFO/LIFO behavior? → Queue / Stack
Start with the Problem Requirements

How often will data change?
-
Frequent inserts/deletes → Linked List, HashMap
-
Mostly read-only → Array (compact, cache-friendly)
Know the Big O basics:
-
Array: O(1) access, O(n) insert/delete in middle
-
Linked List: O(1) insert/delete (if pointer known), O(n) access
-
HashMap/Set: O(1) average insert/lookup, but no order
-
Tree (BST, AVL, Red-Black): O(log n) search/insert/delete, ordered
-
Heap: O(log n) insert/remove-min, O(1) peek
-
Queue/Stack: O(1) push/pop/enqueue/dequeue
Consider Time Complexity

-
Arrays: contiguous, memory efficient, but resizing costs
-
Linked Lists: extra pointers → more memory overhead
-
Hash-based structures: need space for buckets
Consider Space & Memory
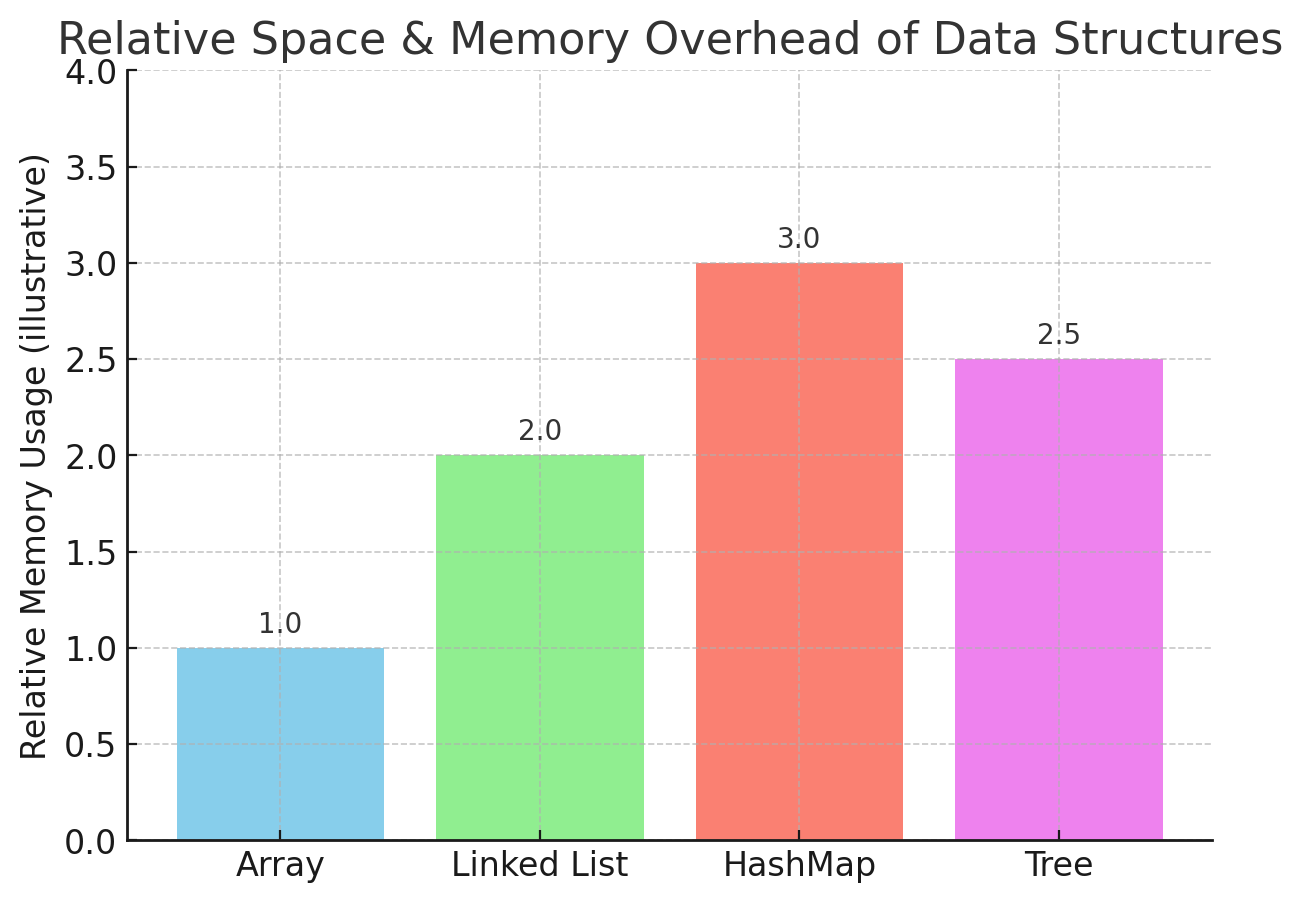
Maximum input size?
Consider Constraints & Edge Cases
| Constraints | Array | Linked List | HashMap | Tree |
|---|---|---|---|---|
| Handles huge input | ✅ | ✅ | ✅ | ✅ |
| Allows duplicates | ✅ | ✅ | ❌ | ✅ |
| Maintains order | ✅ | ✅ | ❌ | ✅ |
| Random access | ✅ | ❌ | ❌ | ❌ |
| Fast updates | ❌ | ✅ | ✅ | ✅ |
Do you need to handle duplicates?
Do you need random access?
Is order important?
-
Autocomplete system → Trie for prefix searches
-
Scheduling tasks by priority → Priority Queue (Heap)
-
Browser back/forward navigation → Stack
-
Streaming data → Queue
-
Tracking unique IDs → Set
-
Fast lookup by key → HashMap
Real-Life Scenarios


Collaborative Live-coding
Designing a Stack
class Stack {
push(element) {}
pop() {}
peek() {}
isEmpty() {}
print() {}
};
-
Define a Stack class that follows the LIFO (Last In, First Out) principle.
-
Implement core methods:
-
push(element) - add item to the top.
-
pop() - remove and return the top item.
-
peek() - view the top item without removing it.
-
isEmpty() - check if the stack is empty.
-
print() - print all items as a string
-
-
Demonstrate usage by pushing and popping values.
-
Focus on efficiency and encapsulation of internal storage.
Designing a Binary Search Tree
class Node {}
class BinarySearchTree {
/**
* Add new Node
* @param {number} value
* @return this // to allow method chaining
*/
add(value) {}
/**
* Find Node by value
* @param {number} value
* @return Node || null
*/
find(value) {}
/**
* Check if Node exists
* @param {number} value
* @return {boolean}
*/
contains(value) {}
traverseInOrder(node = this.root) {}
traversePreorder(node = this.root) {}
traversePostorder() {}
};
-
Implement a Node class with value, left, and right child references.
-
Create a BinarySearchTree class to manage insertion, search, and deletion of nodes.
-
Implement main methods: add, find, and contains.
-
Implement traversal methods: traverseInOrder (sorted), traversePreorder, and traversePostorder.
-
Demonstrate usage by inserting sample values and printing traversal results.
-
Emphasize correctness of BST property (left < root < right).
var MyHashMap = function() {
};
/**
* @param {number} key
* @param {number} value
* @return {void}
*/
MyHashMap.prototype.put = function(key, value) {
};
/**
* @param {number} key
* @return {number}
*/
MyHashMap.prototype.get = function(key) {
};
/**
* @param {number} key
* @return {void}
*/
MyHashMap.prototype.remove = function(key) {
};
/**
* Your MyHashMap object will be instantiated and called as such:
* var obj = new MyHashMap()
* obj.put(key,value)
* var param_2 = obj.get(key)
* obj.remove(key)
*/Design a HashMap without using any built-in hash table libraries.
Implement the MyHashMap class:
- MyHashMap() initializes the object with an empty map.
- void put(int key, int value) inserts a (key, value) pair into the HashMap. If the key already exists in the map, update the corresponding value.
- int get(int key) returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key.
- void remove(key) removes the key and its corresponding value if the map contains the mapping for the key.
var MyLinkedList = function() {
};
/**
* @param {number} index
* @return {number}
*/
MyLinkedList.prototype.get = function(index) {
};
/**
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtHead = function(val) {
};
/**
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtTail = function(val) {
};
/**
* @param {number} index
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtIndex = function(index, val) {
};
/**
* @param {number} index
* @return {void}
*/
MyLinkedList.prototype.deleteAtIndex = function(index) {
};
/**
* Your MyLinkedList object will be instantiated and called as such:
* var obj = new MyLinkedList()
* var param_1 = obj.get(index)
* obj.addAtHead(val)
* obj.addAtTail(val)
* obj.addAtIndex(index,val)
* obj.deleteAtIndex(index)
*/Implement the MyLinkedList class:
- MyLinkedList() Initializes the MyLinkedList object.
- int get(int index) Get the value of the index node in the linked list. If the index is invalid, return -1.
- void addAtHead(int val): Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list.
- void addAtTail(int val): Append a node of value val as the last element of the linked list.
- void addAtIndex(int index, int val): Add a node of value val before the indexth node in the linked list. If index equals the length of the linked list, the node will be appended to the end of the linked list. If index is greater than the length, the node will not be inserted.
- void deleteAtIndex(int index) Delete the indexth node in the linked list, if the index is valid.
Quiz time
Q & A


Thank you!
Useful resources

Time complexity Big 0 for Javascript Array methods and examples can be found in this article
Algorithms and Data structures: Part 2
By Inna Ivashchuk
Algorithms and Data structures: Part 2
- 1,348



