Priority queues

A priority queue is an abstract data structure which supports two main operations:

1. Adding an element to the queue
2. Popping the element with the highest priority

Applications

• Heap sort.
• A* algorithm.
• Huffman encoding.
• Prim's MST algorithm.
• Discrete event-driven simulation.
• Network bandwidth management.
• Dijkstra's shortest-paths algorithm
• Optimization to many dynamic programming algorithms

* we will discuss some of these in the future lectures

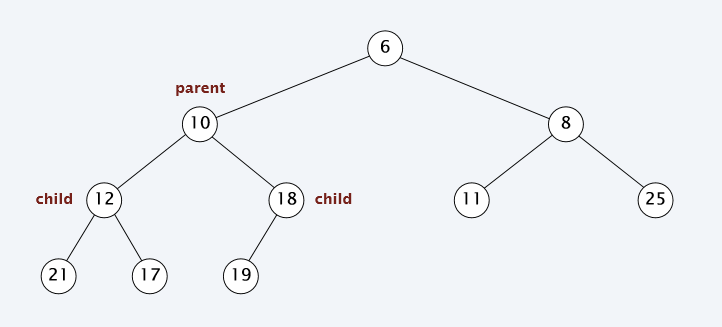
Binary heap

The binary heap is an effective implementation of the priority queue structure.

It represents a perfectly balanced binary tree (except for the last level) with the following property:

For each child, the key in child <= key in parent. (max heap)

or

For each child, the key in child >= key in parent. (min heap)

min-heap

Operations

The (max)heap supports the following operations:

1. Insert an element - O(log n)
2. Retrieve the max element - O(1)
3. Remove the max element - O (log n)
4. Heapify - given a list, construct a heap from it - O(n)

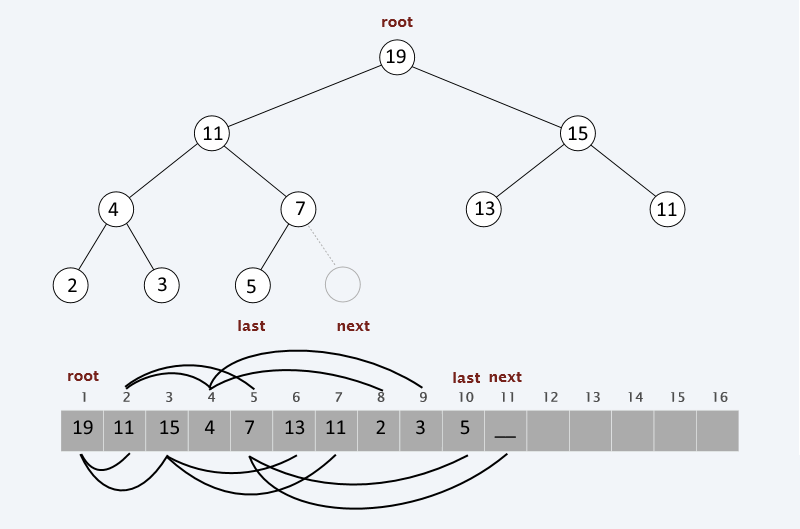
Representation

The heap can be represented as a standard binary tree - nodes with pointers

or implicitly - as an array or list

Representation

The standard representation uses nodes with pointers to both children

class Node {
    Key value;
    Node leftChild;
    Node rightChild;
}

The implicit representation uses the following index rules which ensure that the list will be filled consecutively

Root is at index 1;
Node with index i has children:
    Left: 2*i
    Right: 2*i+1
Node with index i has parent:
    Parent: floor(i/2)

*Note: to implement insert and remove we need a pointer to the next node(from the previous slide) which we can get with O(1) in the implicit representation

Insert

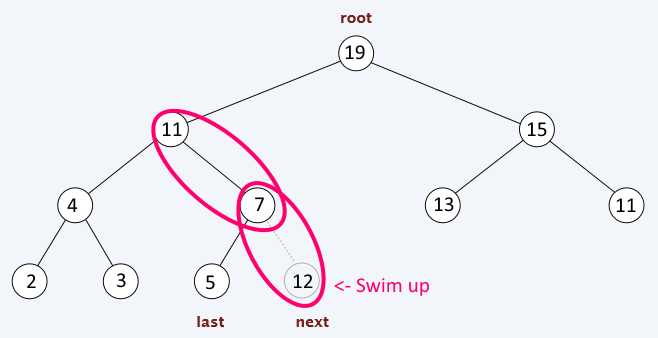
Steps:

Put the new element to the next position

Assign current = inserted element

WHILE current != root AND current > parent(current)

             swap( current, parent(current))

             current = parent(current)

Update the next position

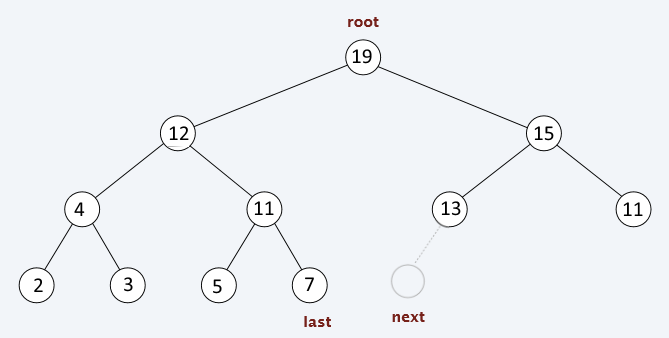
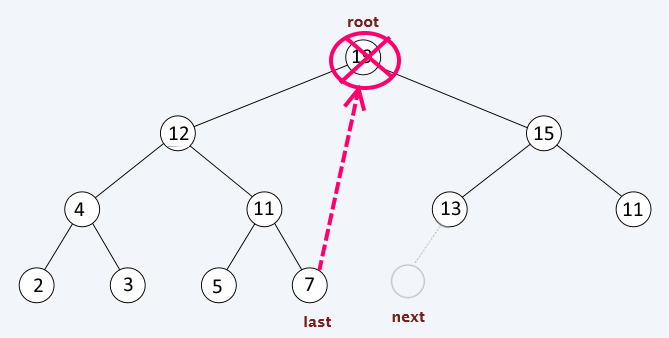
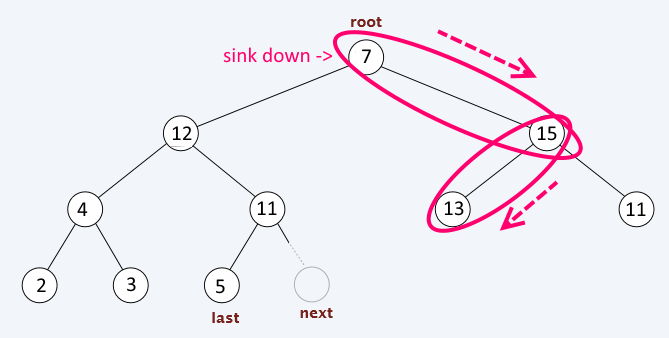
Remove

Steps:

Put the last value over the root value

Assign current = root

WHILE (has_left_child(current) AND current < left(current)) OR (has_right_child(current) AND current < right(current))

             swap( current, larger_child(current))

             current = larger_child(current)

Update the next position

Heapify

Task: Given N elements, construct a binary heap containing them.

Observation: we can insert  each element consecutively and achieve O(n log n)

Bottom-up method: a faster approach - O(n). Goes from the bottom to the top of the tree and applies the same method as in remove (sink down - see previous slide)

Steps:

For i = n to 1

    Assign current = nodes[i]

    WHILE (has_left_child(current) AND current < left(current)) OR (has_right_child(current) AND current < right(current))

             swap( current, larger_child(current))

             current = larger_child(current)

Heapify

Task: Given N elements, construct a binary heap containing them.

Observation: we can insert  each element consecutively and achieve O(n log n)

Bottom-up method: a faster approach - O(n). Goes from the bottom to the top of the tree and applies the same method as in remove (sink down - see previous slide)

Steps:

For i = n to 1

    Assign current = nodes[i]

    WHILE (has_left_child(current) AND current < left(current)) OR (has_right_child(current) AND current < right(current))

             swap( current, larger_child(current))

             current = larger_child(current)

The bottom-up method is faster because it makes use of the fact that most of the nodes in a binary tree are near the bottom and there are fewer levels to go down for these nodes