Binary search tree

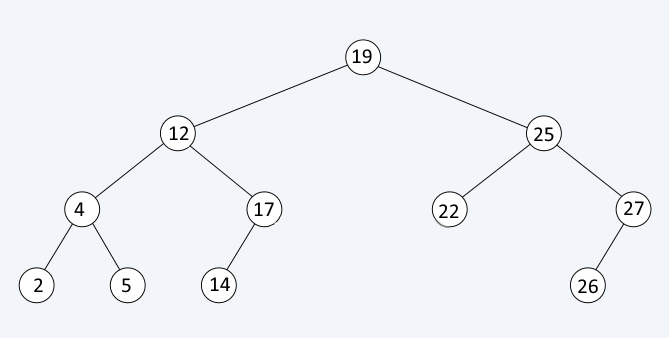
The binary search tree is a binary tree which holds ordered data. The ordering rule is as follows:

the value in each node is greater than the value in its left child and less than the value in its right child.

Applications

The data in a BST is basically always kept sorted and this allows to quickly lookup existing elements. Insert and remove are also fast, having complexities proportional to the tree height.

• Data structures where data is constantly entering/leaving and a quick lookup is needed - map, set
• Used as a base structure for many database engines
• Used in computer graphics for determining object intersection

Representation

The operations in a BST often require redirecting pointers to parents or children, so the most effective representation is by using pointers

class Node
{
    Key value;
    Node leftChild;
    Node rightChild;
}

Operations

The Binary Search Tree supports the following operations:

• Insert element - O(log n)
• Remove element - O(log n)
• Lookup element - O(log n)
• Traverse in sorted order - O(n)

Insert

Insert starts from the root and compares the value of the element being inserted against the value of the existing node in order to decide in which subtree it should go. When there is no child at the link we should follow, insert the new element there

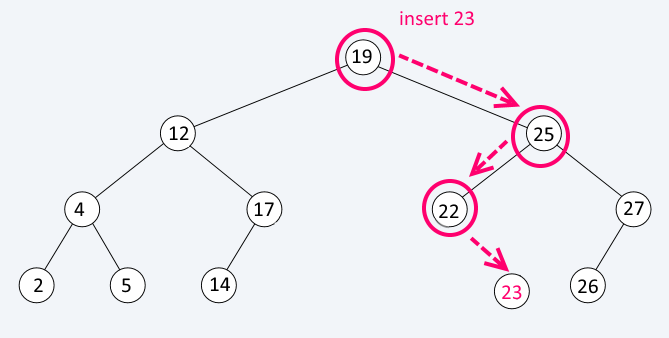
Insert

Insert(inserted value)

     1. Assign current = root

     2. Repeat

                If: current.value > inserted value

                          If: has_left_child(current)

                                  current = left_child(current), then goto 2

                          else:

                                  create_left_child(current, inserted value)

                If: current.value <= inserted value

                          If: has_right_child(current)

                                  current = right_child(current), then goto 2

                          else:

                                  create_right_child(current, inserted value)

Lookup

Lookup goes the same way as the insert - start from the root, compare values and follow one of the links.

Lookup(value)

     Assign current = root

     While current != null

                If: current.value == value

                                  return current

                If: current.value > value

                                  current = left_child(current)

                If: current.value < value

                                  current = right_child(current)

Remove

Remove first finds the element, then finds the leftmost node in its right sub-tree and swaps their values. Then executes Remove recursively for that leftmost node. If a node to be removed has only one child, we can just redirect the links. If a node to be removed does not have any children, just remove it.

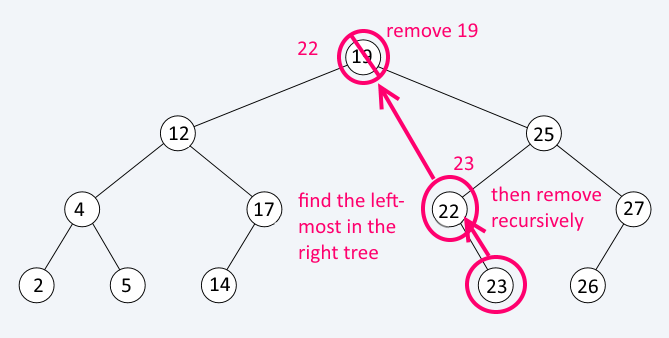
Remove

Remove(node) // should lookup the node before remove

    current = node

    If has_no_children(current)

           remove_from_parent(current)

    else if has_one_child(current)

           replace_in_parent(current, only_child(current))

    else

           replacement = left_most_child(current.right)

           current.value = replacement.value

           Remove(replacement)

Traverse

Traversing a tree is basically going through each of its nodes in a specific order

Pre-order

go through the current, then through the left subtree, then through the right

Preorder-Traverse(node)

            Print(node)

            Preorder-Traverse(node.left)

            Preorder-Traverse(node.right)

In-order

go through the left subtree, then through the current, then through the right

Preorder-Traverse(node)

            Preorder-Traverse(node.left)

            Print(node)

            Preorder-Traverse(node.right)

*Note: this will gives us the sorted sequence

Post-order

go through the left subtree, then through the right, then through the current

Preorder-Traverse(node)

            Preorder-Traverse(node.left)

            Preorder-Traverse(node.right)

            Print(node)

Balancing

The shape of the binary tree depends on the input data. In the worst case (inserting sorted values) it will look like a list

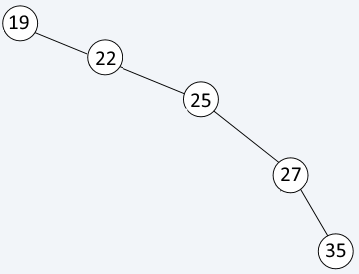
In this case operations will have complexity of O(n)

To resolve this issue, we need to balance the tree (on the figure - make 25 the root)

Balancing

Balancing turns out to be quite a complex task. There are different modifications of the BST which keep the data balanced. Some of them are:

• Red-black tree - marks some of the links as red and others as black and uses this to represent a 2,3-tree like a normal BST.
• AVL-tree - compares the heights of subtrees and applies rotations where needed. The first balanced BST invented.
• Treap - asigns random integers to nodes and tries to keep the heap rule for them (tree + heap = treap). Applies rotations to keep the heap rule.

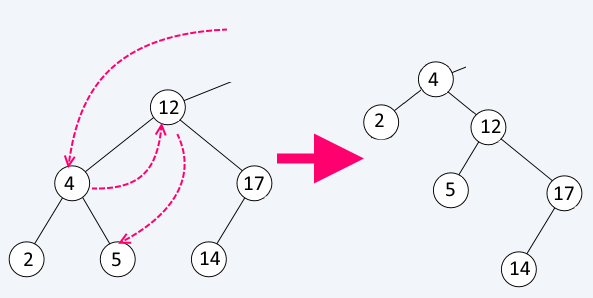
Balancing - rotations

Rotation is a operation which keeps the BST rule but changes the height of subtrees. Rotations are used by Treap and AVL trees to keep the tree balanced. There are two types of rotation: left rotation and right rotation - bringing the left child or the right child up