Algoritmo de Prim

Algoritmo de Prim
Conceptos Previos

Grafo Conexo
Un grafo o grafica es un conjunto finito de nodos o vértices conectados a través de aristas, los cuales pueden ser conexos, es decir existe algún enlace con cada nodo a través de algún camino formando así un grafo entero.

se dice que una grafica es conexa si existe un camino simple entre cualquiera dos de sus vertises.
Grafica de Arbol.
Se dice que una grafica G es de tipo arbol si G es una grafica conexa sin siclos.
Arbol Recubridor Minimo
Dado un grafo conexo y no dirigido, un árbol recubridor mínimo de ese grafo es un subgrafo que tiene que recorrer todos los vértices del grafo inicial.

Algoritmo de Prim
Definición

El algoritmo ..
Incrementa continuamente el tamaño de un árbol, comenzando por un vértice inicial al que se le van agregando sucesivamente vértices cuya distancia a los anteriores es mínima. Esto significa que en cada paso, las aristas a considerar son aquellas que inciden en vértices que ya pertenecen al árbol.
El árbol recubridor mínimo está completamente construido cuando no quedan más vértices por agregar.
La idea básica consiste en añadir, en cada paso, una arista de peso mínimo a un árbol previamente construido.
Objetivo del Algoritmo
Encontrar el árbol recubridor más corto y de menor peso.
Requisitos
- Ser un grafo conexo.
- Ser un grafo sin ciclos.
- Tener todos los arcos etiquetados.

Algoritmo de Prim
Ejemplos !!
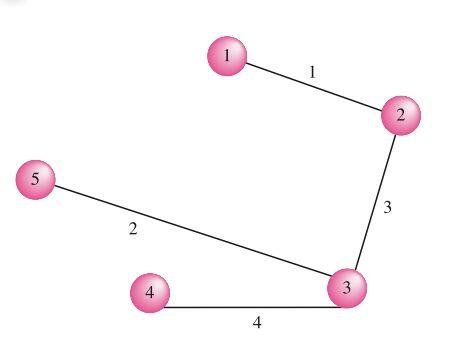
A continuación se presenta un ejemplo de uso del algoritmo de Prim para encontrar el árbol abarcador de costo mínimo de una gráfica:


Grafo Ejemplo 2
- Tiene 6 nodos y 9 aristas
- Es conexo
- Y esta etiquetado
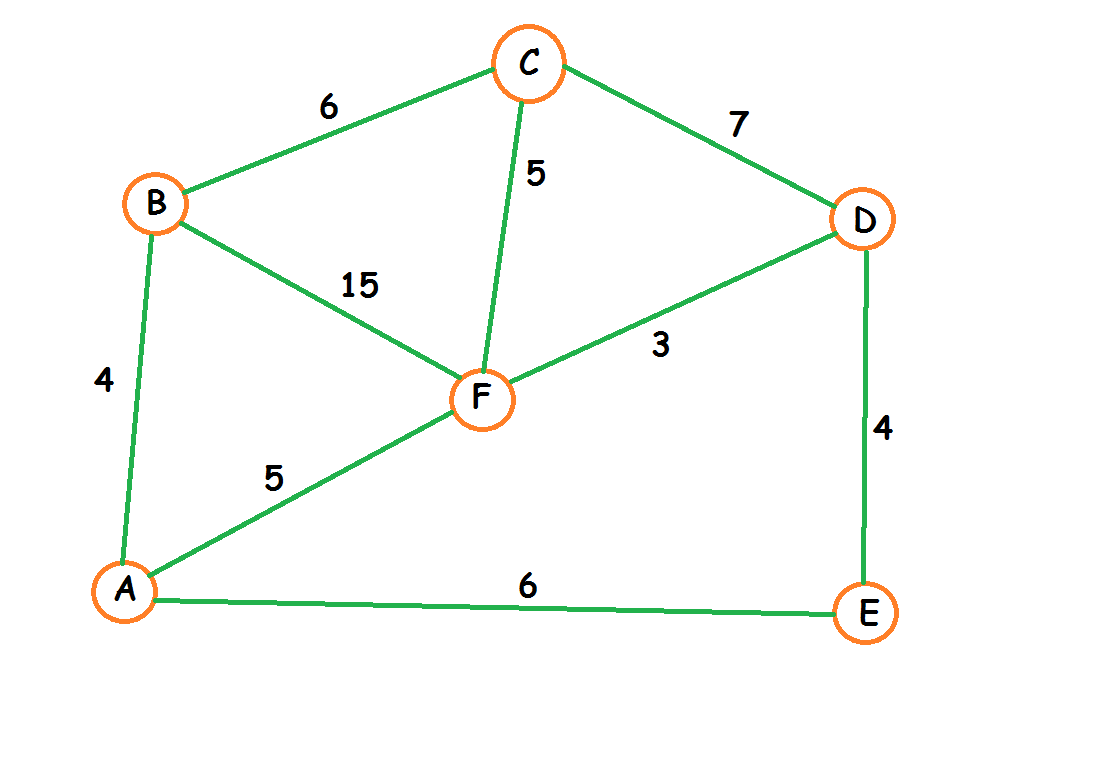
Arbol recubridor minimo Peso 34
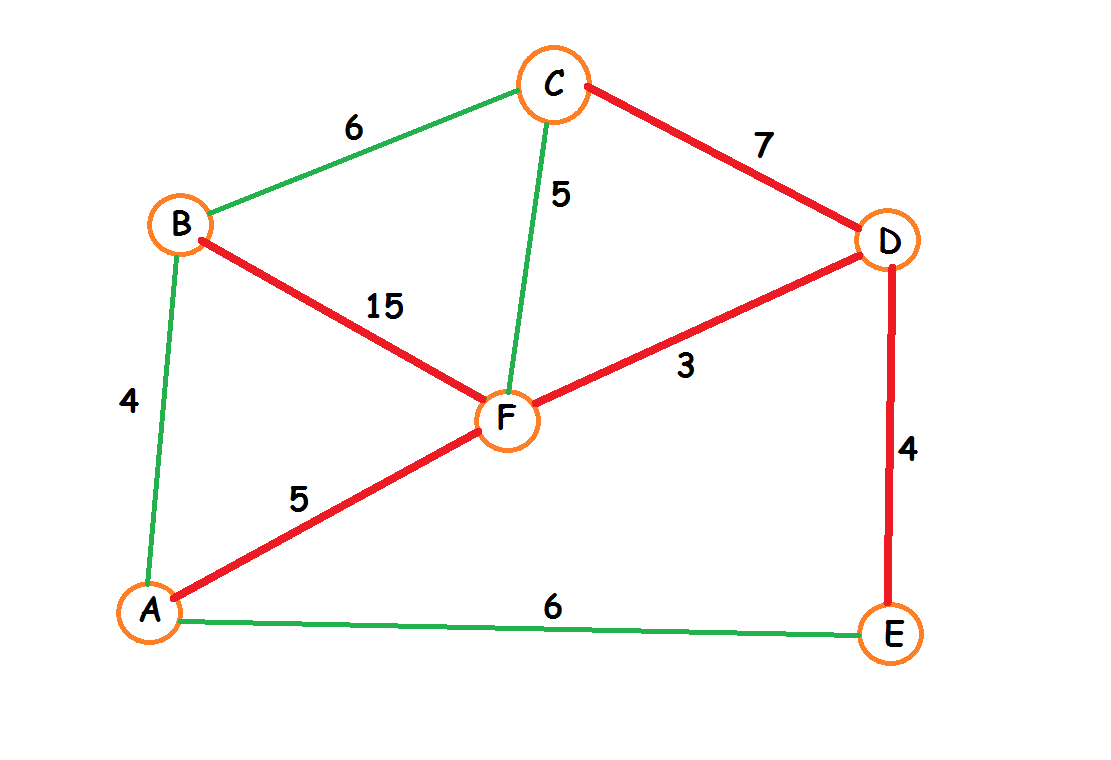
Arbol recubridor minimo Peso 36
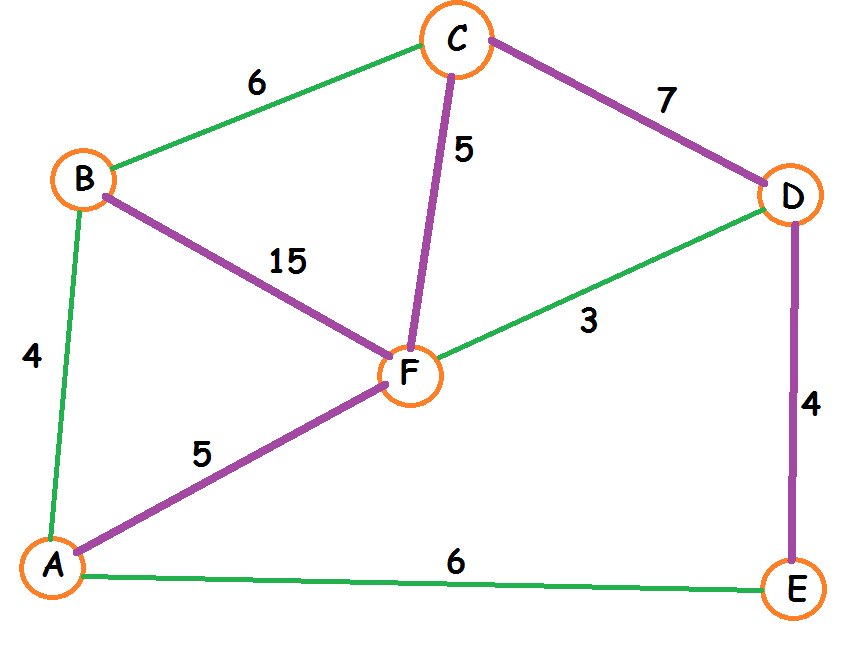
ARM de peso Optimo (21)
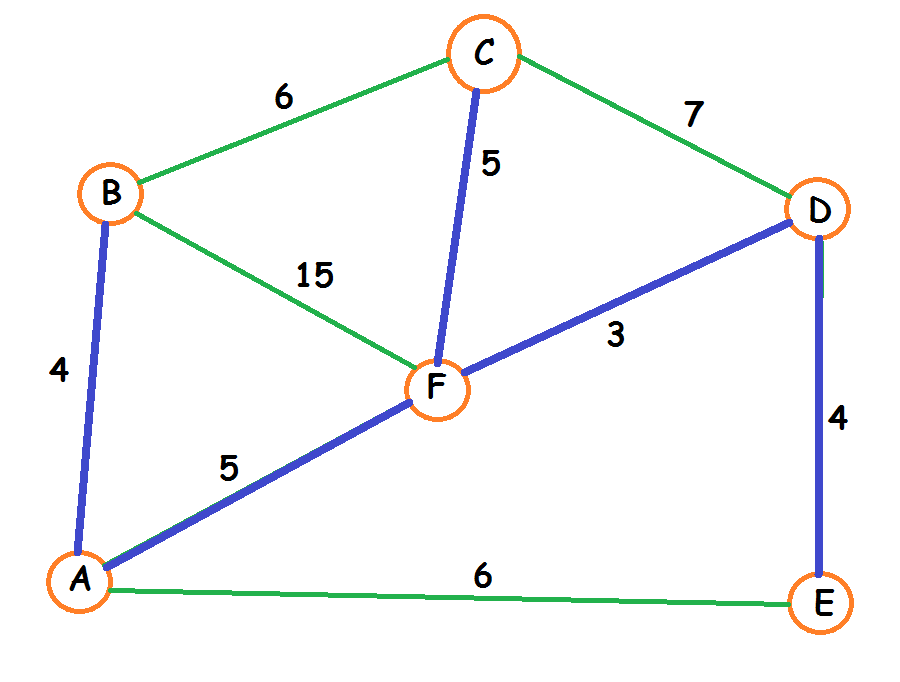
Como Obtener el ARM aplicando Prim?

No es necesario empezar por la arista de menor peso, podemos seleccionar un nodo al azar.

Demostracion con codigo Vamos allá !!!

Copy of Algoritmo de Prim
By Jack O Lantern
Copy of Algoritmo de Prim
- 984



