Please distribute
contraction & Inflation
CC-By 4.0 James B. Wilson, 2024
Contractions & Entropy
-
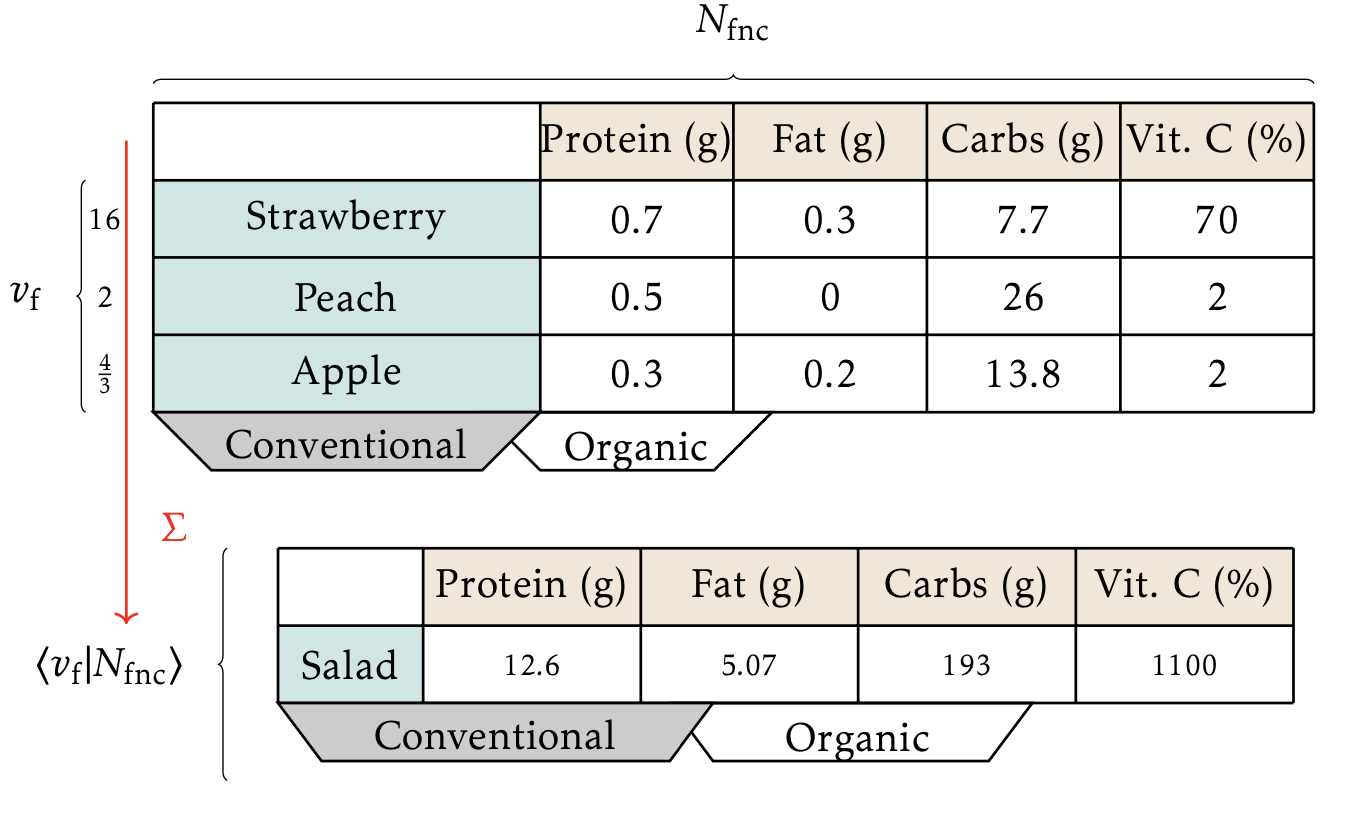
Data table \(T\)
-
User recipe of rows \(v\)
-
Contraction \(\langle u\mid T\rangle\) is newly generated data.
Contractions need recipes
-
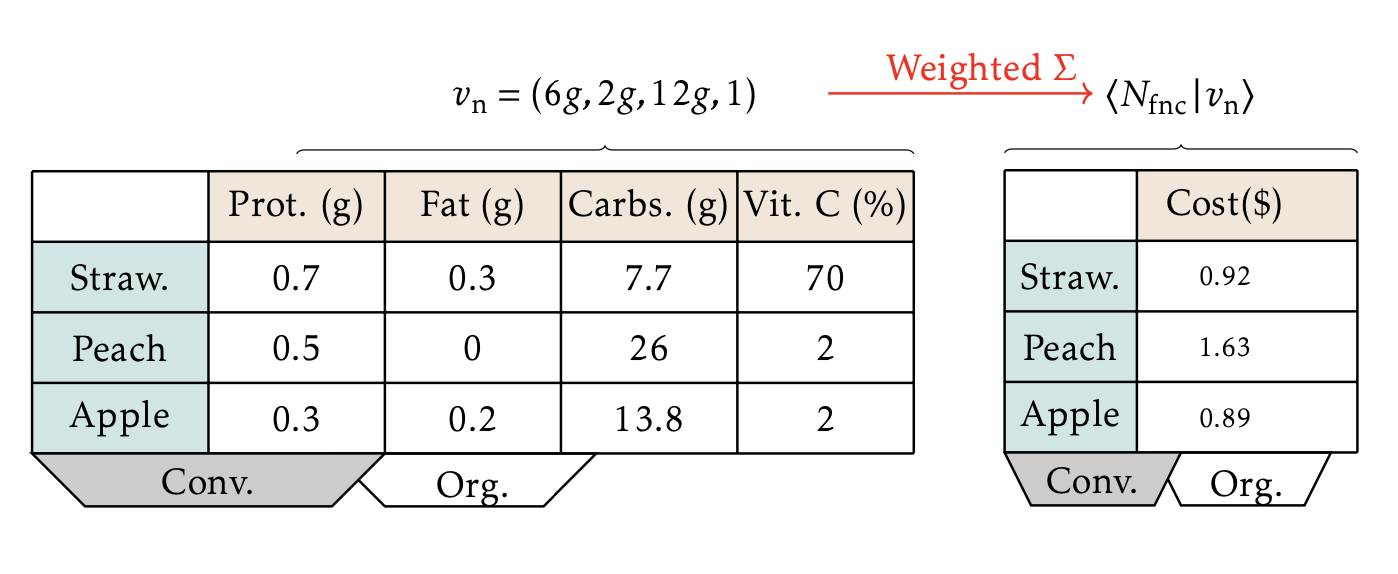
Data table \(T\)
-
User recipe for columns \(v\)
-
Contraction \(\langle T\mid v\rangle\) is newly generated data.
Multiple Contractions allowed
Entropy of contractions
- The order of contractions is immaterial to the result.
- Entropic ("disorder") means operators that applied in any order are the same.
- Commutative? Associative? No, these are different operators, not one operator with rewriting rules.
Entropy
\begin{pmatrix}
\begin{bmatrix}
u_{11} \\ \vdots \\ u_{m1}
\end{bmatrix}
\cdots
\begin{bmatrix}
u_{1n} \\ \vdots \\ u_{mn}
\end{bmatrix}
\end{pmatrix}
=\begin{bmatrix}
\begin{pmatrix}
u_{11} & \cdots & u_{1n}
\end{pmatrix}\\
\vdots \\
\begin{pmatrix}
u_{m1} & \cdots & u_{mn}
\end{pmatrix}
\end{bmatrix}
Given products \((u_1,\ldots,u_n)\) and \(\begin{bmatrix} v_1\\ \vdots\\ v_m\end{bmatrix}\)
Entropy
=
Main Example
Inflation & Distribution
-
Recepies \(u,v,w\)
-
Build a product \(u\otimes v\otimes w\) whose partial evaluations are entropic.
Inflation produces tables
Product Notations
\begin{gather*}
u*v,\quad uv, \quad \langle u|v\rangle,\quad [u,v]\\
\langle u_1,\ldots,u_{\ell}\rangle, \quad [u_1,\ldots,u_{\ell}]
\end{gather*}
Functional notation \[u:\text{axes}\to \text{space}\] so partition axes to partition input.
\langle u_a+\acute{u}_a, u_{\bar{a}}\rangle = \langle u_1,\ldots, u_a+\acute{u}_a,\ldots, u_{\ell}\rangle
tensor spaces
-
Data table \(T\)
-
First recipe of rows \(u\)
-
Second recipe \(\acute{u}\)
-
Contract \[\langle u+\acute{u}\mid T\rangle=\langle u\mid T\rangle+\langle \acute{u}\mid T\rangle.\]
Multiple recipes
measurement distributes
Even in limits
\int_a^b (f+g) \text{d}x=\int_a^b f \text{d}x +\int_a^b g\text{d}x
\int_{I\sqcup J} f \text{d}x=\int_I f \text{d}x +\int_J f\text{d}x
measurement Is contextual
- River's length is in miles/km
- River's depth is in feet/meters.
- Volume in gallons/liter
- \[\text{vol}(t\mid \text{length}, \text{depth}, \text{width})\]
- USA \(t=39,500 \text{gal}/\text{mile}\times \text{ft}^2\)
- EU \(t=1 \text{l}/1000 \text{km}^2\times \text{m}\)
Convention is not the point. In binary both conversions are bizzare choices.
Definition.
A tensor space is a distinguished term of a distributive product.
A tensor is an term/element of a tensor space.
Definition.
A cotensor space is the type of outputs of a distributive product.
A cotensor is an term/element of a cotensor space.
| Interpretation | Tensors | Valence |
|---|---|---|
| Area/Volume/... | Measure | 2,3,... |
| Markov process | Distribution | 2 |
| Cost functions | costs | 1 |
| Distributed computing | Thread pool | any |
Potential tensor spaces
| Interpretation | Tensors | Valence |
|---|---|---|
| Logic/circuits | gates (and/or...) | 2,3,... |
| Foundations | Distribution | 2 |
| hom, tensor product,... | Categories | 2,3... |
Potential tensor spaces
The implication
Data Table
Multiplication Table
The point:
\begin{aligned}
x^2 & = -2-3x\\
x^2+3x+2 & = 0\\
(x+1)(x+2) & = 0
\end{aligned}
Data Table
Multiplication Table
The point
Algebra has 1200 year head start on organizing data.
The requirement
(u+\acute{u})*(v+\acute{v})
u*(v+\acute{v})+\acute{u}*(v+\acute{v})
(u*v+u*\acute{v})+(\acute{u}*v+\acute{u}*\acute{v})
(a+b)+(c+d)=(a+b)+(c+d)
(u+\acute{u})*v + (u+\acute{u})*\acute{v}
(u*v+\acute{u}*v)+(u*\acute{v}+\acute{u}*\acute{v})
Medial Law: a special case of entropy
-
Current distributes proportional to resistance
-
\(I=R_1 I_1+R_2 I_2\)
-
New addition \[I_1\boxplus I_2=R_1 I_1 +R_2 I_2\] is medial.
Ohms law
Eckmann-Hilton Argument
A medial addition with a 0 is a both commutative and associative.
Commonoid = "Commutative Monoid"
To play nice with products add axiom:
\[\forall a \qquad \langle 0_a,u_{\bar{a}}\rangle=0\]
Grothendieck.
Every commoind has associated to it an abelian group to which it is maximally embedded.
Fact. If negatives exist then they already play nice \[\forall a \qquad \langle -u_a,u_{\bar{a}}\rangle=-\langle u_a,u_{\bar{a}}\rangle\]
Murdoch-Toyoda.
Every medial quasigroup is an affine twist of an abelian group.
\[x\boxplus y=Mx+Ny+b\]
Quasi-group: \(a+x=b\) and \(x+a=b\) has unique solutions.
Tensor take products Cotensors make products
Tensor Contractions & Inflations
By James Wilson
Tensor Contractions & Inflations
Tensors are defined by having contractions and cotensors by inflation. What are these and what do they require?
