Image Convolution for meta-data
2021 James B. Wilson, Colorado State University

- - - - -
* * * * * - + + + + + -
* * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * - + + -
* * * * * - + + + + + -
- - - - -
Convolution
Original Goals:
- sharpen an image,
- find edges,
- find textures, etc.
In the past it was for "photo-shop" (trade mark?).
Today its image feature extraction to give to machine learning.
1 1 1
0 _ 0 --> 3
0 0 0\begin{aligned}
\begin{bmatrix}
1 & 1 & 1\\
0 & 0 & 0\\
-1 & -1 & -1
\end{bmatrix}
&
\boxtimes
\begin{bmatrix}
a & b & c\\
d & e & f\\
g & h & i\\
\end{bmatrix}
\to \begin{bmatrix}
1\cdot a & 1\cdot b & 1\cdot c\\
0\cdot d & 0\cdot e & 0\cdot f\\
-1\cdot g & -1\cdot h & -1\cdot i\\
\end{bmatrix}
\\
& \to
a+b+c-g-h-i
\end{aligned}
Image Convolution
0 0 0
0 _ 0 --> -3
1 1 10 0 1
0 _ 0 --> 0
1 0 01 1 1
1 _ 0 --> 2
1 0 00 0 1
0 _ 1 --> -2
1 1 11 0 1
1 _ 1 --> 0
1 0 11 1 1
1 _ 1 --> 0
1 1 11 0 0
0 _ 0 --> 1
0 0 00 0 0
0 _ 0 --> -1
0 1 0\begin{aligned}
\begin{bmatrix}
a & b & c & d\\
e & f & g & h\\
i & j & k & l\\
\end{bmatrix}
& \to
\left[
\begin{bmatrix}
a & b & c \\
e & f & g \\
i & j & k \\
\end{bmatrix}
,
\begin{bmatrix}
b & c & d\\
f & g & h\\
j & k & l\\
\end{bmatrix}
\right]\\
& \to
\left[
\begin{bmatrix}
1 & 1 & 1 \\
0 & 0 & 0 \\
-1 & -1 &-1 \\
\end{bmatrix}
\boxtimes
\begin{bmatrix}
a & b & c \\
e & f & g \\
i & j & k \\
\end{bmatrix}
,
\begin{bmatrix}
1 & 1 & 1 \\
0 & 0 & 0 \\
-1 & -1 &-1 \\
\end{bmatrix}
\boxtimes
\begin{bmatrix}
b & c & d\\
f & g & h\\
j & k & l\\
\end{bmatrix}
\right]\\
\end{aligned}
Image Convolution
0 0 0 1 0 0 0 0 0 1
0 0 0 1 --> 0 _ 0 0 _ 1 --> [ -3, -2 ]
1 1 1 1 1 1 1 1 1 11 1 0 0 1 1 0 1 0 0
0 0 0 0 --> 0 _ 0 0 _ 0 --> [ 1, -1 ]
0 0 1 1 0 0 1 0 1 1 + + + + + + +
* * * * * + + + + + + + + +
* * * * * * * + + + + + + + +
* * * * * * * * * + + + + + +
* * * * * * * * *
* * * * * * * * *
* * * * * * * * *
* * * * * * * * * - - - - - -
* * * * * * * - - - - - - - -
* * * * * - - - - - - - - -
- - - - - - -
Detect horizontal edges
Now working on the interior we can step through all the points and record if the answer is + or -.
Here are the results on a octagon.
+ + - -
* * * * * + + + - - -
* * * * * * * + + + + - - - -
* * * * * * * * * + + + - - -
* * * * * * * * * + + - -
* * * * * * * * * + + - -
* * * * * * * * * + + - -
* * * * * * * * * + + + - - -
* * * * * * * + + + + - - - -
* * * * * + + + - - -
+ + - -\begin{bmatrix}
1 & 0 & -1\\
1 & 0 & -1\\
1 & 0 & -1
\end{bmatrix}
Convolutions detecting Verticality
Use a different mask, notice it detect something different, similar to the mask...
- - - - -
* * * * * - + + + + + -
* * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * * * - + + -
* * * * * * * - + + -
* * * * * - + + + + + -
- - - - -
\begin{bmatrix}
0 & -1 & 0\\
-1 & 4 & -1\\
0 & -1 & 0
\end{bmatrix}
All around edge detection?
Only near the edges do we find nonzeros.
Convolution Tensors
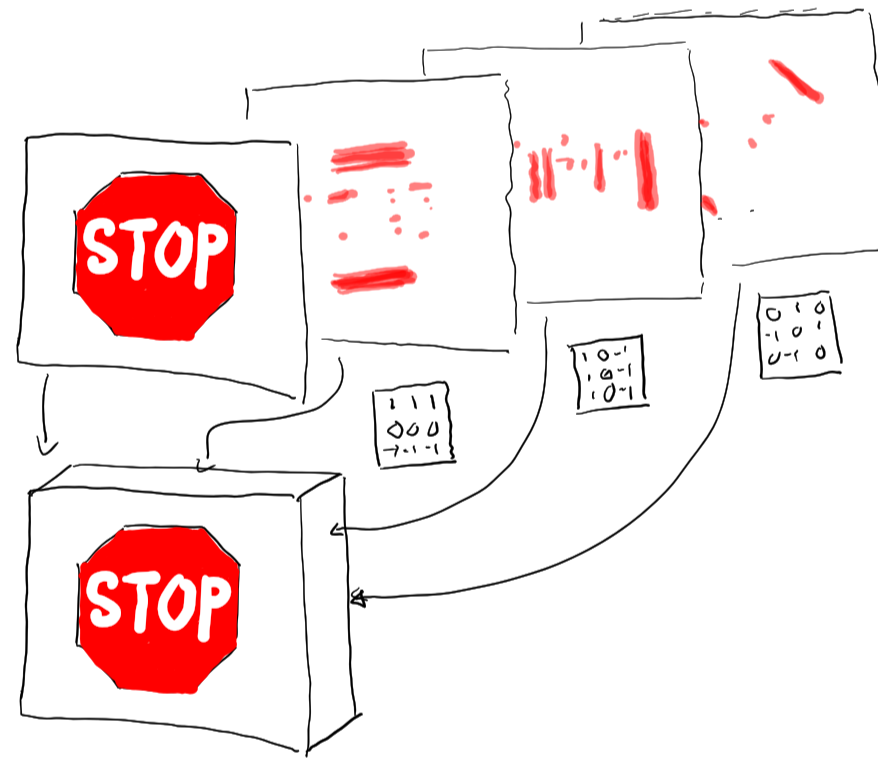
Inert Axis
Linear Axis
Image Meta Data
By James Wilson
Image Meta Data
Basic image convolution
- 650


