Foundations of Entropy III

 

 MaxEnt and related stuff

 

 

Lecture series at the 

School on Information, Noise, and Physics of Life

Nis 19.-30. September 2022

 

by Jan Korbel

all slides can be found at: slides.com/jankorbel

Activity III

 

You have 3 minutes to write down on a piece of paper:

             

Have you been using entropy in

your research/ your projects? 

 

If yes, how?

 

 

 

My applications: statistical physics, information theory, econophysics, sociophysics, image processing...

"You should call it entropy, for two reasons: In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have the advantage."

John von Neuman's reply to Claude Shannon's question how to name newly discovered measure of missing information

Information entropy = thermodynamic entropy

Maximum entropy principle

Maximum entropy principle

General approach - method of Lagrange multipliers

 Maximize \(L(p) = S(p) - - \alpha \sum_i p_i -  \sum_k \lambda_k \sum_i I_{i,k} p_i\)

$$\frac{\partial L}{\partial p_i} = \frac{\partial S(p)}{\partial p_i} - \alpha - \sum_k \lambda_k I_{i,k} \stackrel{!}{=} 0$$

In case \(\psi_i(P) = \frac{\partial S(p)}{\partial p_i}\) is invertible for \(p_i\), we get that

 

$$ p^{\star}_i = \psi_i^{(-1)}\left(\alpha + \sum_k \lambda_k I_{i,k}\right)$$

Legendre structure of thermodynamics - interpretation of L

$$L(p) = S(p) - \beta U(p) = \Psi(p) = - \beta F(p)$$

free entropy

MB, BE & FD MaxEnt

Maxwell-Boltzmann

\(S_{MB} = - \sum_{i=1}^k p_i \log \frac{p_i}{g_i}\)

\(p_i^\star = \frac{g_i}{Z} \exp(-\epsilon_i/ T) \)

Bose-Einstein

\(S_{BE} =  \sum_{i=1}^k  \left[(\alpha_i + p_i) \log (\alpha_i +p_i) - \alpha_i \log \alpha_i - p_i \log p_i\right]\)

\(p_i^\star = \frac{\alpha_i}{Z} \frac{1}{\exp(\epsilon_i/ T)-1} \)

Fermi-Dirac

\(S_{FD} =  \sum_{i=1}^k  \left[-(\alpha_i - p_i) \log (\alpha_i -p_i) + \alpha_i \log \alpha_i - p_i \log p_i\right]\)

\(p_i^\star = \frac{\alpha_i}{Z} \frac{1}{\exp(\epsilon_i/ T)+1} \)

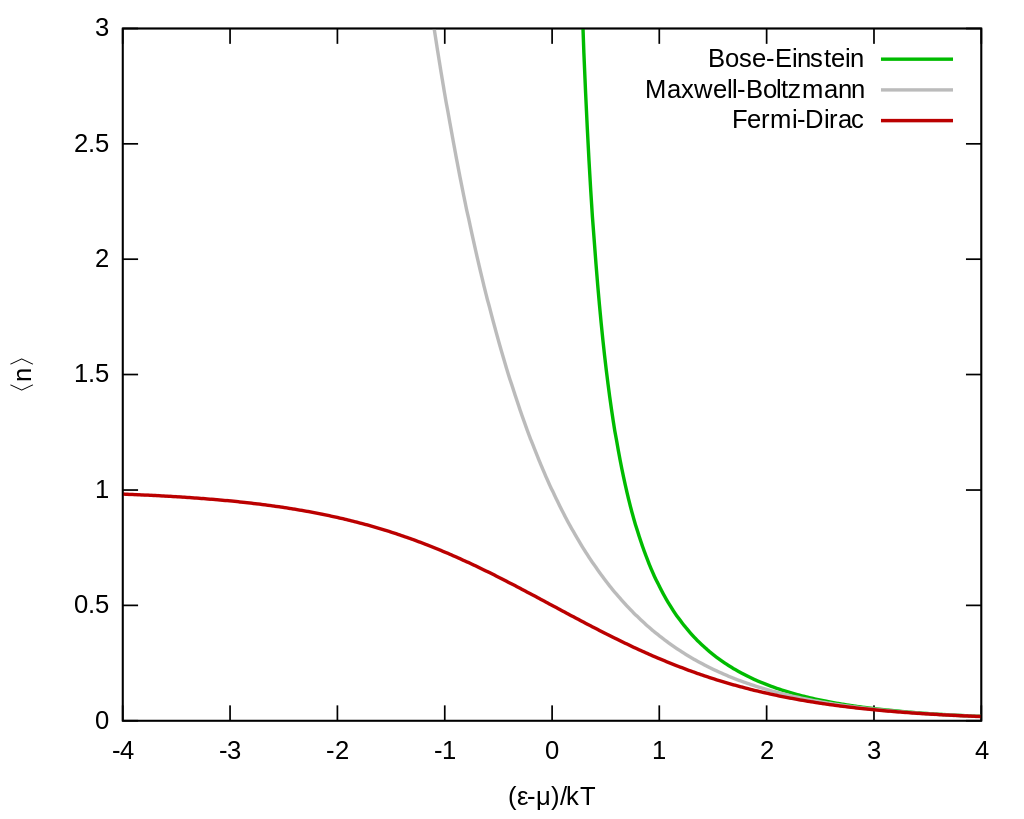
MB, BE & FD MaxEnt

Structure-forming systems

$$S(\wp) =- \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} - 1) - \sum_{ij} \wp_{ij} \log \frac{j!}{n^{j-1}}$$ 

Normalization: \(\sum_{ij} j \wp_{i}^{(j)} =1 \)             Energy: \(\sum_{ij} \epsilon_{i}^{(j)} \wp_{i}^{(j)} = U\)

where \( j \wp_i^{(j)} =  p_i^{(j)}\)

MaxEnt distribution:     \(\wp_i^{(j)} = \frac{n^{j-1}}{j!} \exp(-\alpha j -\beta \epsilon_i^{(j)})\)

The normalization condition gives  \(\sum_j j \mathcal{Z}_j e^{-\alpha j} = 1 \) 

where \(\mathcal{Z}_j = \frac{n^{j-1}}{j!} \sum_i \exp(-\beta \epsilon_i^{(j)}) \) is the partial partition function

We get a polynomial equation in \(e^{-\alpha}\)

Average number of molecules \(\mathcal{M} = \sum_{ij} \wp_{i}^{(j)}\)

Free energy: \(F = U - T S = -\frac{\alpha}{\beta} - \frac{\mathcal{M}}{\beta} \)

MaxEnt of Tsallis entropy

$$S_q(p) = \frac{\sum_i p_i^q-1}{1-q}$$

MaxEnt distribution is: \(p_i^\star = \exp_q(\alpha+\beta \epsilon_i)\)

Note that this is not equal in general to  \(q_i^\star =\frac{\exp_q(\beta \epsilon_i)}{\sum_i \exp_q( \beta \epsilon_i)}\)

However, it is possible to use the identity

$$\exp_q(x+y) = \exp_q(x) \exp_q\left(\frac{y}{\exp_q(x))^{1-q}}\right)$$

 

The MaxEnt distribution of Tsallis entropy can be expressed as

$$p_i^\star(\beta) = \exp_q(\alpha+\beta \epsilon_i) = \exp_q(\alpha) \exp_q(\tilde{\beta}\epsilon_i) = q_i^\star(\tilde{\beta}) $$

where \( \tilde{\beta} = \frac{\beta}{\exp_q(\alpha)^{1-q}}\)

(sometimes called self-referential temperature)

MaxEnt for path-dependent processes

and relative entropy

 

• What is the most probable  histogram of a process \(X(N,\theta)\)?
  • \(\theta\) - parameters, \(k\) histogram of \(X(N,\theta) \)
  • \(P(k|\theta)\) is probability of finding a histogram
• ​Most probable histogram \(k^\star = \argmin_k P(k|\theta) \)
• In many cases, the probability can be decomposed to $$P(k|\theta) = W(k) G(k|\theta)$$
  •  \(W(k)\) - multiplicity of histogram
  • \(G(k|\theta)\) - probability of a microstate belong to \(k\)
• $$\underbrace{\log P(k|\theta)}_{S_{rel}}= \underbrace{\log W(k)}_{S_{MEP}} + \underbrace{\log G(k|\theta)}_{S_{cross}} $$
  • ​\(S_{rel}\) - relative entropy (divergence)
  • \(S_{cross}\)- cross-entropy, depends on constraints given by \(\theta\)

The role of constraints

The cross-entropy corresponds to the constraints

For the case of expected energy, it can be expressed through the cross entropy

$$S_{cross}(p|q) = - \sum_i p_i \log q_i $$

where \(q_i\) are prior probabilities. By taking \(q^\star_i = \frac{1}{Z}e^{-\beta \epsilon_i}\) we get

$$S_{cross}(p|q^\star) = \beta\sum_i p_i \epsilon_i + \ln Z$$

However, for the case of path-dependent process, the natural constraints might not be of this form

Kullback-Leibler divergence

$$D_{KL}(p||q) = -S(p) + S_{cross}(p,q) $$

$$S_{SSR}(p) = - N \sum_{j=2}^n \left[p_i \log \left(\frac{p_i}{p_1}\right) + (p_1-p_i) \log \left(1-\frac{p_i}{p_1}\right)\right]$$

MaxEnt for SSR processes

From multiplicity of trajectory histograms, we have shown that the entropy of SSR is

Let us now consider that after each run (when the system reaches the ground state) we drive the ball to a random state with probability \(q_i\)

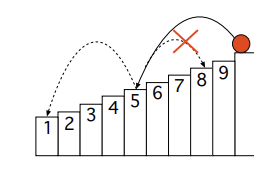
After each jump the effective space reduces

MaxEnt for SSR processes

One can see that the probability of sampling a histogram \(k_i\) is 

$$G(k|q) = \prod_{i=1}^n \frac{q_i^{k_i}}{Q_{i-1}^{k_i}} $$

where \(Q_i = \sum_{j=1}^i q_i\) and \(Q_0 \equiv 1\).

$$S_{cross}(p|q) = - \sum_{i=1}^n p_i \log q_i - \sum_{i=2}^n p_i \log Q_{i-1} $$

By assuming in \(q_i \propto e^{-\beta \epsilon_i}\) the cross-entropy is

$$S_{cross}(p|q) = \beta \sum_{i=1}^n p_i \epsilon_i + \beta \sum_{i=2}^n p_i f_i = \mathcal{E} + \mathcal{F}$$

where \(f_i = \ln \sum_i e^{-\beta \epsilon_i}\)

MaxEnt for Pólya urns

Probability of observing a histogram

$$ p(\mathcal{K}) =  \binom{N}{k_1,\dots,k_c} p(\mathcal{I}) $$

By carefully taking into account the initial number of balls in the urn \(n_i\) we end with

$$S_{Pólya}(p) = - \sum_{i=1}^c \log(p_i + 1/N)$$

$$S_{Pólya}(p|q) = - \sum_{i=1}^c \left[\frac{q_i}{\gamma} \log \left(p_i + \frac{1}{N}\right) - \log\left(1+\frac{1}{N\gamma} \frac{q_i - \gamma}{p_i+\frac{1}{N}}\right)+ \log q_i\right]$$

where \(q_i = n_i/N, \gamma=\delta/N\)

Long-run limit

$$S_{Pólya}(p) = - \sum_{i=1}^c \log p_i$$

$$S_{Pólya}(p|q) = - \sum_{i=1}^c \left[\frac{q_i}{\gamma} \log p_i + \log q_i\right]$$

By taking \(N \rightarrow \infty\), we get

Related extremization principles

As we already found out, the MaxEnt principle can be seen as a special case of the principle of minimum relative entropy

$$p^\star = \arg\min_p D(p||q)$$

In many cases, the divergence can be expressed as \(D(p||q) = - S(p) + S_{cross}(p,q)\)

It connects information theory, thermodynamics and geometry

Priors \(q\) can be obtained from theoretical models or measurements

Posteriors \(p\) can be from parametric family or from a special class of probability distributions

Relative entropy is well defined for both discrete and continuous distributions

Maximization for trajectory probabilities - Maximum caliber

Let us now consider the whole trajectory \(\pmb{x}(t)\) with probability \(p(\pmb{x}(t))\)

We define the term caliber, which is the KL-divergence of the path probability

 

$$S_{cal}(p|q) = \int \mathcal{D} \pmb{x}(t) p(\pmb{x}) \log \frac{p(\pmb{x}(t))}{q(\pmb{x}(t))}$$

N.B.: Entropy production can be written in terms of caliber as

 

$$\Sigma_t = S_{cal}[p(\pmb{x}(t))|\tilde{p}(\tilde{\pmb{x}}(t))]$$

Review on MaxEnt & MaxCal

MaxCal and Markov processes

Other extremal principles in ThD

Prigogine's principle of minimum entropy production

Principle of maximum entropy production (e.g., for living systems)

Further reading

MaxEnt as an inference tool

Maximum entropy principle consists of two steps:

The first step is a statistical inference procedure.

The second step gives us the connection to thermodynamics.

Entropy 23 (2021) 96

Exercise: what is the relation between Lagrange multipliers 

between Tsallis entropy  \(S_q = \frac{1}{1-q} \left(\sum_i p_i^q-1\right) \)

and Rényi entropy \(R_q = \frac{1}{1-q} \ln \sum_i p_i^q\)?

Summary